剥开零知识证明的洋葱
- Krishang
- 发布于 2024-12-16 16:31
- 阅读 2155
通过讲解证明者和验证者之间的关系,以及如何使用 ZKP 实现隐私保护的机制。文中零知识证明的基本原理与公式,举例说明 Tornado Cash 如何通过零知识证明确保用户交易的匿名性
- 原文链接:zk.bearblog.dev/introduction
- 译者:AI翻译官,校对:翻译小组
- 本文链接:learnblockchain.cn/article…
剥开零知识洋葱
2024 年 11 月 27 日
本文由一位工程师爱好者撰写(嗨,我是 Krishang 👋🏽),为同样的工程师和爱好者们。
文章主要基于我对 RareSkills ZK Book 的阅读,以及 zksecurity 的文章、重建 Tornado Cash 和其他相关探索。
本文介绍了零知识(ZK),使你具备足够的概念知识,以便探索工具并构建项目,而不会感到完全像个角色扮演者(LARP)。
我们将适度剥开零知识洋葱,让你感到“哦,这就是它的真正含义”,而不会用你并不真正需要了解的数学吓到你(但你可以选择在之后自行探索)。
高级介绍
在“零知识证明”中涉及两个参与方——_证明者_和验证者。
证明者(prover):
- 知道一些数据 $d$
- 满足一组约束 $C$
- 通过另一组数据 $P_d$ 证明他对该数据的知识。
验证者(Verifier):
- 知道一组约束 $C$
- 从_证明者_那里接收数据 $P_d$
- 无法从 $P_d$ 中检索原始数据 $d$
- 但可以检查 $P_d$,以验证_证明者_知道一些满足约束 $C$ 的数据 $d$。
因此,“零知识证明”算法是一个过程,允许_证明者_说服验证者,让他相信他知道一些满足给定约束的特定数据,而不透露该数据本身。
“零知识”证明是_证明者_向_验证者_提供的数据,_验证者_可以检查这些数据,以确定_证明者_是否诚实地声明他对原始未透露数据的知识。
使这个过程零知识的原因在于,_证明者_从未向任何人透露原始数据 d,以证明他知道 d。
正式介绍
数据 d 是特殊的,因为它满足_证明者_和_验证者_都关心的一组约束 C。这组约束可以被视为对某些数据的描述,而对其他数据则不成立。
例如,一个约束可以简单地表示为:a×b=42
这个约束实际上是对所有乘积为 42 的对 (a,b) 的描述。尽管这个例子非常简单且是虚构的,但它捕捉了一个深刻的原则——一组算术约束是对一组数据的描述——特别是,满足这些约束的数据集。
换句话说,我们可以理解零知识证明为_证明者_说服验证者,让他相信他知道某个特定集合的成员,而不透露具体是哪个成员。
一组算术约束是一个方程组:
- $z^3+43=x^2·y$
- $y−22= \sqrt x+3z$
- ... 依此类推
方程组的解是所有出现在方程中的变量的值分配(例如 (x,y,z)=??)。一个方程组可以没有解、一个解或多个解。
零知识证明的目的是使_证明者_能够证明他知道一个方程组的变量 (v1,v2,...vn) 的值分配,该值分配满足所有方程,而不透露特定的值分配。
在任何零知识证明的高级应用中,例如混币器(Tornado Cash)、zkVM、私人投票等,在低级别上,都有一个方程组来编码应用的高级“问题”。
实际介绍
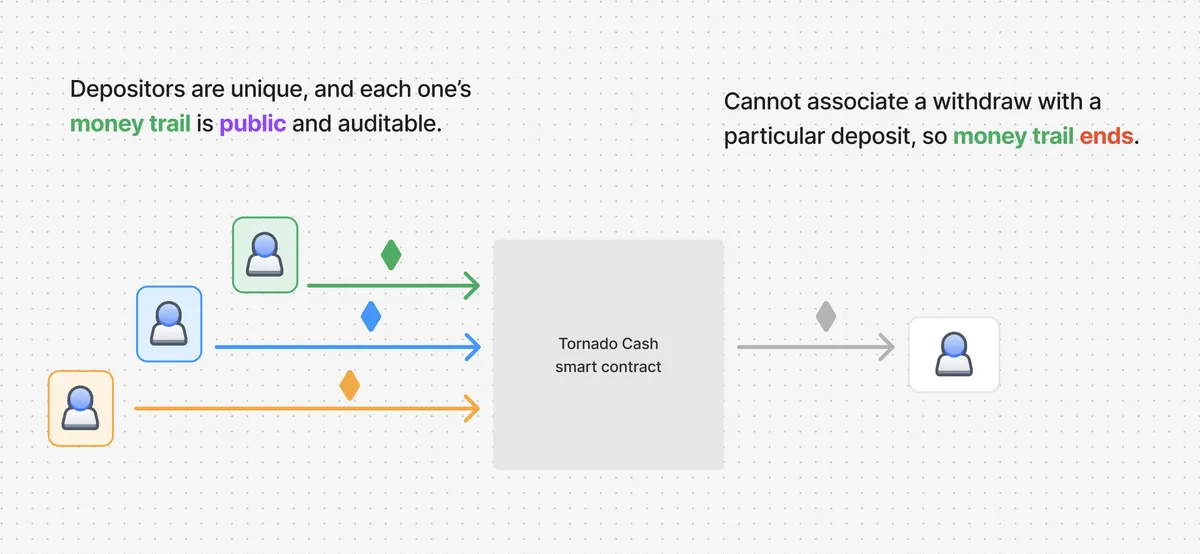
Tornado Cash 的“问题”是让一个账户(Alice)将 1 个以太币存入其智能合约,并允许另一个账户(Bob)在不创建 Alice 和 Bob 之间任何可识别关联的情况下提取 Alice 的存款。
Tornado Cash 通过让存款人提交一个_承诺_与他们的存款一起提交来实现这一点。这个承诺是将两个值哈希在一起的输出。
$$C=hash(n,s)$$
其中 C 被称为承诺,而 n,s(_无效值_和秘密)是仅存款人知道的私有值。智能合约现在只会在提取者证明他们知道 n,s 时释放该存款金额。
为了证明这一点,如果提取者必须向智能合约直接或间接但可恢复地透露 n,s,就会有可能在特定存款和提取之间创建关联。这是因为我们可以简单地从所有存款中查找承诺值 C,并检查哪个满足 $C=hash(n,s)$。
为了避免在存款和提取之间创建任何关联,Tornado Cash 使用零知识证明算法 Groth-16 允许提取者证明他们知道与特定存款相关的某些 n,s。在这里,智能合约充当验证者,而提取者充当证明者。
Tornado Cash 于 2019 年首次推出。自那时以来,ZK 工具不断发展,使得原始代码库有些过时。我们将通过 tornado-cash-rebuilt 仓库进行讲解,该仓库使用现代 Solidity 和 ZK 工具重建 Tornado Cash 以供教育目的。
/circuits 目录包含使用 Circom 编写的代码。该代码定义了编码我们刚刚学习的 Tornado Cash 中心“问题”的算术约束集。
从这个电路代码中,我们能够生成 Verifier.sol 智能合约,该合约充当某个无效值 n 和秘密 s 的 Groth-16 知识证明的验证者,使得 C=hash(n,s) 对于与存款一起发送到 Tornado Cash 智能合约的某个承诺 C 成立。
最后,ETHTornado.t.sol 测试文件演示了以下的端到端流程:
- 选择一个随机的无效值 n 和秘密 s。
- 生成承诺 C=hash(n,s) 并使用它进行存款。
- 生成零知识证明并使用它进行提取。
本文介绍了零知识的基本概念,使你具备了足够的概念知识,现在可以探索工具并构建项目。
也就是说,我们刚刚开始剥开洋葱,还有许多层需要继续探索。
- Lean 4 工程化入门:Elan 工具链配置与 Lake 包管理实战 565 浏览
- 第17章. 零知识证明 1367 浏览
- 050:可验证计算(Verifiable Computation):让智能在链上被信任 2878 浏览
- 044:ZK:隐私与可验证性的双刃剑 1833 浏览
- Passkey ECDSA 验证的 ZKP 系统基准测试 1562 浏览
- GARUDA: Faster SNARKs via Equifficient Polynomial Commitments 1214 浏览
- GARUDA and PARI: Faster and Smaller SNARKs via Equifficient Polynomial Commitments 1186 浏览
- ZKLogin 与隐私增强身份验证 2209 浏览
- 零知识证明:证明,而无需泄露数据 2108 浏览
- 最终,一个数字信任的新世界 1144 浏览
- 超立方体 IR:零知识证明系统的基础 2038 浏览
- 零知识虚拟机(zkVM)入门:原理、分类与应用全景图 4033 浏览