KZG 多项式承诺及其在区块链中的应用（EIP-4844）

KZG 多项式承诺及其在区块链中的应用（EIP-4844）。

在密码学中，多项式是表示关于各种实体知识的强大工具。例如，一组数字可以通过插值作为一个多项式表示。同样，计算也可以通过算术电路转化为多项式。因此，能够以一种方式承诺一个多项式，使得承诺者在发送承诺值后不能更改该多项式，同时保持该多项式的秘密，在密码学中是非常有价值的。此外，承诺可以用来在任意位置公开多项式。多项式承诺方案，特别是 KZG 方案，解决了这个问题，并作为许多保护隐私的密码协议的构建块。KZG 多项式承诺还是零知识证明（ZKP）协议的基本组成部分，例如 zkSNARKs。在这篇文章中，我打算详细阐述 KZG 方案及其在区块链中的应用，特别是以太坊 2.0 的最新 EIP-4844（Proto-Danksharding）。让我们开始吧！

基础知识

定义

承诺方案是一个加密协议，允许一方（承诺者）承诺一个选定的值，同时对其他方保持隐藏，并能够在稍后阶段揭示承诺的值。承诺可以以一种方式发送给另一方（验证者），一旦发送，承诺者就不能更改这个承诺为另一个值。验证者可以使用这个承诺在值揭示后来验证承诺的值。这种能力在需要隐私保护和机密性的密码协议中至关重要。

承诺的值可以是任意消息、单个值、向量或多项式。为每种类型的承诺值设计了各种协议。多项式承诺是承诺方案的一个子领域，专门处理作为承诺值的多项式。正如前面提到的，在密码学中，特别是在区块链中，“ 知识”经常被转化为多项式。因此，多项式承诺作为许多保护隐私的协议的基础。

回想一下，n 次多项式是一个函数，如下所示。

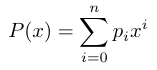
其中：

• p_i 为多项式的系数。
• n 为多项式的度数。KZG 方案支持的最大度数为 n=2²⁸ 。

属性

作为承诺方案的多项式承诺具有两个主要属性。

绑定性

承诺方案的绑定属性确保一旦值被承诺，承诺者就不能将其更改为另一个值。在多项式承诺中，承诺绑定到承诺的多项式上。

隐藏性

承诺方案的隐藏属性确保承诺的值对于所有方（除了承诺者和验证者）是隐藏的。承诺的值仅由承诺者向验证者揭示，以便通过承诺来验证。在多项式承诺中，承诺的多项式保持隐藏。

相

一般而言，多项式承诺或承诺方案由两个阶段组成。

承诺阶段

在承诺阶段，承诺者选择一个值并生成一个承诺，即一段隐藏所选择值的数据。这个承诺随后被发送给验证者。承诺不应该揭示任何关于原始值的信息。在多项式承诺中，承诺可以被视为基础多项式的“指纹”。这些承诺被设计为简洁的，并且可能在链上发布，就像 KZG 承诺方案和 EIP-4844 所看到的那样。

揭示阶段

在揭示阶段，承诺者向验证者揭示原始值，验证者随后利用承诺对该值进行验证。在多项式承诺中，基础多项式在这一阶段揭示。

多项式承诺的一个独特价值主张是能够在特定点“打开”多项式，而不是揭示其所有系数。具体而言，承诺者通过提供该点的多项式值及其评估的“ 证明”向验证者打开多项式。验证者随后可以利用承诺和证明来验证评估。换句话说，验证者并不知道整个多项式，但可以验证该多项式在给定点的某个值的评估。这一属性在密码学和区块链应用中尤其有用。

Merkle 树

作为一个例子，让我们回顾一下区块链中的一个广为人知的方案：Merkle 树。实际上，Merkle 树是一个向量承诺方案，而不是一个多项式承诺方案。然而，我认为回顾Merkle 树对理解承诺方案的术语和一般概念是有价值的。

Merkle 树是一个类似于二叉树的数据结构。在这个树中，叶节点包含任意数据的哈希。非叶节点包含其子节点的哈希的串联。根节点是最顶部的节点，代表整个数据结构的哈希。下图展示了深度为4的Merkle树。

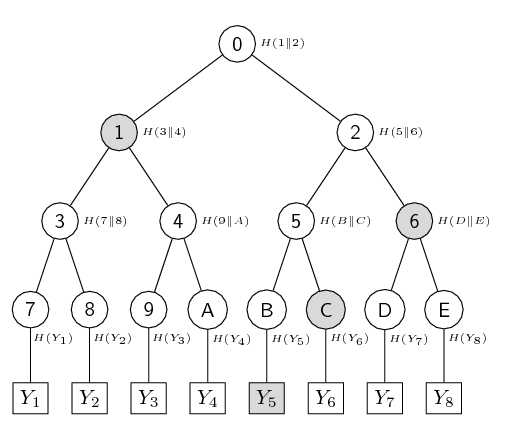
深度为4的Merkle树。

假设Merkle树的深度为 d。叶节点可以表示为一个包含 2^d 元素的向量，例如 a_0, a_1, …, a_2^d-1。Merkle 根作为对这个向量的承诺。绑定属性表明，一旦进行了承诺，承诺者就不能改变为另一棵树，否则将在揭示阶段拒绝Merkle根。

为了证明一个元素 a_i 位于向量的索引 i，承诺者需要提供一个由 d 个哈希组成的证明。给定Merkle根（承诺）和证明，验证者可以确认该声明是真的，即某个特定元素确实存在于向量的某个索引中。

实际上，Merkle树可以转换为一个多项式承诺方案。我们稍后将讨论这一点。

KZG 多项式承诺

定义

KZG 多项式承诺是一种承诺方案，以发现它的密码学家 Kate、Zaverucha 和 Goldberg 命名。该方案因其安全性和高效性而著称。KZG 多项式承诺基于椭圆曲线对加密技术。它允许承诺者对一个多项式进行承诺，然后在任何点向验证者打开该多项式，同时对验证者和所有其他方保持该多项式的隐藏。承诺和评估的证明都很小，且大小恒定（48 字节）。揭示阶段的验证也很高效，仅需进行两次配对操作和两次群体乘法，无论多项式的度数如何。此外，多个评估可以聚合为单个证明，从而增强协议的效率。然而，KZG 承诺方案需要一个可信环境，如果攻击者妥协了秘密密钥并利用系统，这可能会降低协议的安全性。

假设承诺的多项式是一个 n 次多项式 P(x)，如下所示。

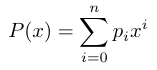
其中：

• p_i 是多项式的系数。
• p_i, x 都是有限域 F_q 的元素。

KZG 多项式承诺方案是建立在一种 配对友好的椭圆曲线 [1] 上，如 BLS12–381，这种曲线定义在有限域 F_q 上，包含两条椭圆曲线 E_1 和 E_2，并支持配对 e，使得。

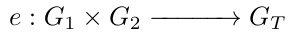
其中：

• G_1, G_2 为 E_1 和 E_2 的群体元素。G, H 为 G_1 和 G_2 的生成元。
• G_T 是目标群体。

我建议阅读我的文章 “BLS 签名” [3] 以清楚理解配对操作。

构建

KZG 多项式承诺由四个阶段组成：可信设置、承诺、创建证明和验证证明。让我们探讨这些阶段。

可信设置

与传统承诺方案不同，KZG 方案需要可信设置。这一步的目的是生成一个名为“ 陷门”的秘密密钥。随后使用这个秘密密钥创建一个公钥，进而用于创建承诺和证明。

作为设置的第一步，需要生成一个秘密密钥 s。它是来自有限域 F_q 的一个随机数。

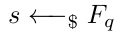
这个秘密密钥可以通过一个隔离的计算机生成，或者通过多方计算（MPC）仪式生成。该步骤的安全性假设是隔离的计算机保持未被入侵，或者并非所有参与者在MPC中都受到入侵。换句话说，秘密密钥不会被公开，因此称为“可信设置”。

然后使用秘密密钥 s 推导出公钥，如下所示。

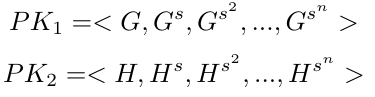
即公钥由 n+1 个点的两个元组构成，这些点在椭圆曲线 E_1 和 E_2 上，对应于一个 n+1 大小的秘密密钥向量 <s⁰, s¹, …, s^n>。

生成公钥后，必须销毁秘密密钥以保持协议的安全性。需要注意的是，公钥可以重用于多个多项式，从而提高协议的效率。

承诺阶段

给定来自可信设置的公钥 PK，承诺者可以生成对多项式 P(x) 的承诺 C，如下所示。

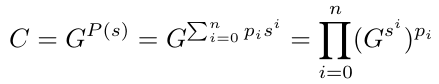
知道多项式的度数 n、公钥组件 G^{s^i} 和多项式系数 p_i，便很容易计算出承诺 C。

承诺绑定于多项式，即 绑定属性 强烈成立。为什么呢？

假设承诺者找到另一个多项式 Q(x)，使得它与多项式 P(x) 具有相同的承诺，即。

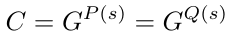
则意味着：

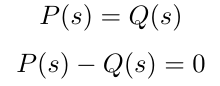
因为承诺者不知道秘密 s，要使得 P(s) — Q(s) = 0 的唯一方式是在尽可能多的地方使 P(x) — Q(x) = 0。令 Z(x) = P(x)-Q(x)，这本身是一个 n 次多项式。陈述 P(x)-Q(x)=0 等价于 Z(x) 在零处的评估。我们知道 n 次多项式最多可以有 n 个零评估。KZG 方案支持的最大度数是 n=2²⁸。假设有 2²⁸ 个点使得 Z(x) 的评估为零，承诺者找到其中任一个点的可能性是 2²⁸ 除以群体的阶，即 q=2²⁵⁵-19。这个可能性几乎为零，约为 2^-227。这意味着在实践中，承诺者不能找到另一个具有相同承诺的多项式。换句话说，承诺绑定于承诺的多项式，且绑定属性强烈成立。

创建证明（即见证）阶段

正如前面提到的，KZG 多项式承诺方案允许承诺者在任何地点向验证者打开多项式。具体而言，承诺者通过呈现某点的多项式评估和此评估的证明向验证者打开多项式。让我们探讨如何生成这个证明。值得注意的是，在原始论文中，作者使用“见证”这个术语，而不是“证明”。然而，为与其他区块链协议一致，在本文章中我们使用“证明”。

假设承诺者想向验证者证明 P(x) 在点 z 处评估得到值 y，即

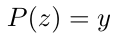
令 A(x)=P(x)-y，这也是一个 n 次多项式。陈述 P(z)=y 意味着 P(z)-y=0，等价于 A(x) 在点 z 的评估为零。根据代数理论，我们知道多项式 A(x) 在点 z 评估为零，当且仅当 x-z 可以整除 A(x)。令 q(x) 为 A(x) 除以 x-z 的商，我们得到。

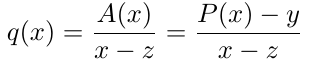
实际上，q(x) 是一个 (n-1) 次多项式。

在类似于承诺 C 的方式下，证明 w（即评估为 P(z)=y 的证明）是如下生成的。

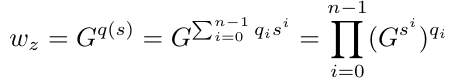
其中 q_i 是商多项式 q(x) 的系数。

验证证明阶段

给定承诺、评估和相应的证明，验证者可以利用配对操作验证证明。如果以下公式成立，则承诺和证明是有效的。

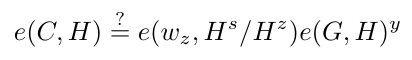
其中：

• C 是多项式 P(x) 的承诺。
• w_z 是评估 P(z)=y 的证明，如前一步所定义。
• s 是秘密密钥。由于秘密密钥 s 对验证者（及所有其他方）是未知的，因此 H^s 是在可信设置中定义的公钥 PK_2 的一个元素。
• G, H 是椭圆曲线 E_1 和 E_2 的生成元。

为什么呢？通过利用配对的双线性映射，我们可以将方程的左边扩展如下。

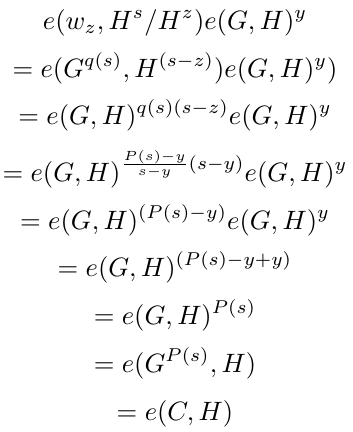
这意味着验证公式成立，因此，多项式评估的正确性得到证明。

我们已经证明了绑定属性在可信设置阶段强烈成立，但隐藏属性呢？实际上，验证者对原始多项式没有任何信息。要验证证明，他仅知晓公钥、承诺、评估值 y 和评估点 z。这表明隐藏属性也强烈成立。换句话说，KZG 是一个安全的多项式承诺方案。

代码示例

下面分享一个 KZG 多项式承诺的代码示例。

signature-schemes/kzg/kzg.py at main · 0xbarchitect/signature-schemes \ \ 对于包括 BLS、ECDSA 和 EdDSA 的流行签名方案的实验代码 - signature-schemes/kzg/kzg.py at…\ \ github.com

安全分析

KZG 多项式承诺的安全性依赖于 离散对数问题（DLP） [2] 和强迭代-海尔曼（SDH）假设。DLP 在密码学中广为人知，而 SDH 假设是在基于配对的密码学中的计算硬度假设。SDH 假设表述如下：

• 设置：考虑一个简单的群 G，其素数阶为 q，生成元为 g。群 G 通常是椭圆曲线上的点的群，配对操作在此群上定义。
• 问题陈述：给定一个元组如下。

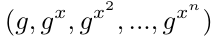
对于某些整数 n，找到一对使得

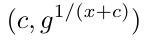
其中 c 是一个整数，是计算上不可行的。

KZG 方案的隐藏属性依赖于 DLP。另一方面，绑定属性在 SDH 假设下得到证明。

类似于 BLS 签名 [3]，KZG 承诺方案的安全级别为 128 位，这意味着理论上需要 2¹²⁸ 次操作才能强行攻击该签名系统。128 位的安全级别被认为对当前的计算能力是安全的。

证明聚合

证明聚合是 KZG 承诺方案的独特价值主张。类似于 BLS 签名方案 [3] 中签名聚合，可以将多个多项式评估的证明聚合为一个证明。通过验证聚合证明，验证者可以确认多项式在这些点的确切评估。聚合证明的大小与单个证明的大小相同，特别是 48 字节。验证一个聚合证明所需的加密操作也不比验证单个证明更多。这种能力减少了在承诺者与验证者之间传输证明数据所需的带宽，并且也减少了验证每个单个证明所需的计算。因此，证明聚合提高了 KZG 方案的效率，特别是在区块链应用中。让我们探讨一下它的工作原理。

创建聚合证明

假设我们希望聚合 k 次对多项式 P(x) 在 k 个点 (z_0, z_1, …, z_k-1) 的评估证明，使得。

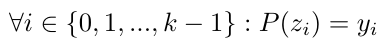
根据代数理论，我们知道存在一个多项式可以通过所有 k 个点 (z_i, y_i)。这个多项式称为插值多项式，它利用 拉格朗日插值 [6] 导出如下。

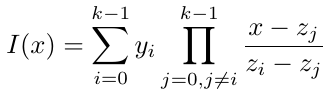
由于 P(x) 和 I(x) 在点 z_i 的评估值相同 y_i，这意味着多项式 P(x) — I(x) 在这些点的评估为零。让我们创建一个多项式 Z(x)，通过将所有线性因子 x-z_i 相乘使得。

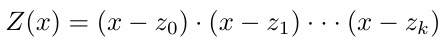
Z(x) 被称为 零多项式。

根据代数理论，我们知道 P(x) — I(x) 在 k 个点 (z_0, z_1, ..., z_k) 评估为零当且仅当 Z(x) 可以整除 P(x) — I(x)。令 q(x) 为 P(x) — I(x) 除以 Z(x) 的商，那么我们有。

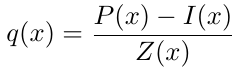
q(x) 本身是一个多项式。

与单一证明类似，聚合证明 w_a 是从公钥和 q(x) 生成的如下。

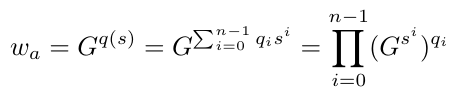
其中 q_i 是商多项式 q(x) 的系数。

验证聚合证明

如果以下方程成立，那么聚合证明有效。

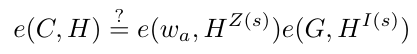
让我们证明这一点。通过利用双线性映射，我们可以将方程的左侧扩展如下。

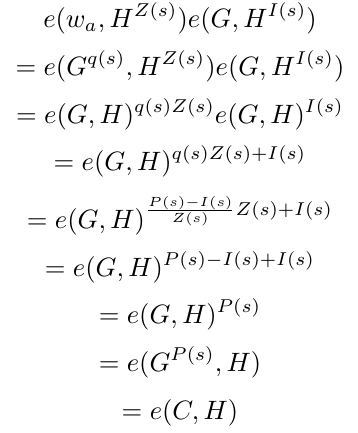
验证方程成立，即聚合证明有效。这也意味着多项式在多个点 z_i 处确实评估为特定的值 y_i。因此，协议的正确性得到了证明。

到目前为止，我们讨论了 KZG 多项式承诺方案的定义和构建以及它的证明聚合能力。在下一节中，我们将探讨其在区块链中的应用，特别是在近期的 EIP-4844 中。

EIP-4844 (Proto — Danksharding)

EIP-4844（即 Proto-Danksharding） [7] 是一项提案，已被批准作为 Dencun 更新的一部分集成到以太坊协议中，计划于 2024 年 3 月实施。该提案引入了一种新的交易类型“ blob-交易”，广泛用于 Layer-2 区块链以高效地将其数据汇聚到 Layer 1。本文并不旨在深入研究 EIP-4844 的细节；相反，它侧重于 KZG 多项式承诺方案在此提案中的应用。

让我们回顾一下提案中定义的 blob-交易的负载。

[chain_id, nonce, max_priority_fee_per_gas, max_fee_per_gas, gas_limit, to, value, data, access_list, max_fee_per_blob_gas, blob_versioned_hashes, y_parity, r, s]

值得注意的是，交易的负载包含一个名为 blob_versioned_hashes 的承诺哈希列表。这些承诺对应于一组 blob 数据，每个数据都由一个多项式表示。blob 数据或原始多项式并不一定提交到区块链。相反，它们会被不永久存储在信标链上，并在短时间后（大约 18 天）被删除。具体而言，存储在信标链上的数据包括承诺、在特定点 z 上评估至特定值 y 的多项式的证明。EIP-4844 还提供了一个预编译，以验证 KZG 证明，如下所示。

def point_evaluation_precompile(input: Bytes) -> Bytes:
    """
    验证 p(z) = y ，给定与多项式 p(x) 对应的承诺和 KZG 证明。
    还验证提供的承诺是否与提供的 versioned_hash 匹配。
    """
    # 数据编码如下：versioned_hash | z | y | commitment | proof | 其中 z 和 y 是填充的 32 字节大端值
    assert len(input) == 192
    versioned_hash = input[:32]
    z = input[32:64]
    y = input[64:96]
    commitment = input[96:144]
    proof = input[144:192]

    # 验证承诺与 versioned_hash 匹配
    assert kzg_to_versioned_hash(commitment) == versioned_hash

    # 在大端格式中验证 KZG 证明的 z 和 y
    assert verify_kzg_proof(commitment, z, y, proof)

    # 返回 FIELD_ELEMENTS_PER_BLOB 和 BLS_MODULUS 作为填充的 32 字节大端值
    return Bytes(U256(FIELD_ELEMENTS_PER_BLOB).to_be_bytes32() + U256(BLS_MODULUS).to_be_bytes32())

通过利用 KZG 多项式承诺，EIP-4844 显著提高了 rollup 的效率。它还显著降低了交易成本；具体而言，EIP-4844 后 Layer-2 的交易成本至少降低了 10 倍，如下表所示。

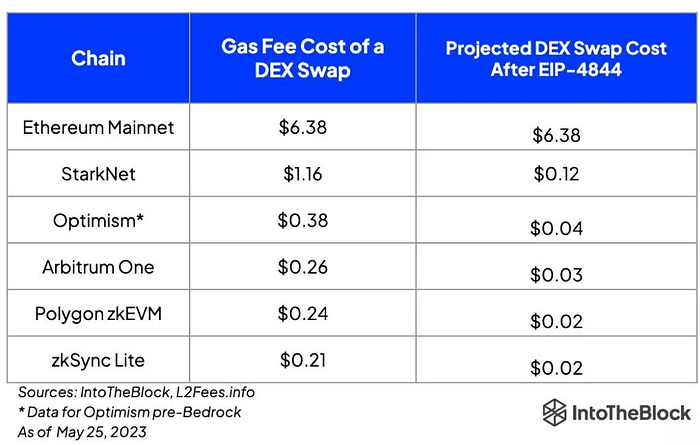
EIP-4844 后交易成本降低。来源 IntoTheBlock。

（附加）KZG 作为向量承诺

如前所述，Merkle 树是一个向量承诺方案。虽然该方案是安全的，但在证明生成和验证方面的效率并不高。实际上，位于索引 i 的叶节点 a_i 的证明包含 log_N 个哈希，其中 N 是叶节点的总数。证明的大小与 Merkle 树大小成线性关系，结果，验证证明所需的计算需求也与树的大小成线性关系。然而，我们可以通过将 Merkle 树转化为 KZG 多项式承诺来提高 Merkle 树的效率。这该如何实现？

回想一下，Merkle 树由 n 个叶节点构成，例如 (a_0, a_1, a_2, …, a_n-1)。因此，Merkle 树可以表示为大小为 n 的向量，其中元素 a_i 位于索引 i。我们还可以将 Merkle 树表示为一组 n 个点 (i, a_i)。根据代数理论，我们知道存在一个多项式能够通过所有这些点。这个多项式可以使用拉格朗日插值确定，如下所示。

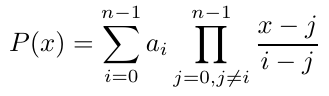
其中：

• a_i 是索引 i 的叶节点
• n 是叶节点的总数

叶节点 a_i 位于索引 i 的声明等同于说多项式 P(x) 在点 i 处的值为 a_i。利用 KZG 多项式承诺，我们可以计算出插值多项式的承诺及其评估的证明。值得注意的是，证明的大小是恒定的，由单个群体元素构成，特别是 48 字节。此外，证明的大小不依赖于 Merkle 树的大小。验证证明也很高效，正如前面部分所讨论的。因此，通过在插值多项式上将 Merkle 树转化为 KZG 方案，我们显著提高了协议的效率。

结论

KZG 多项式承诺方案是构建保护隐私的密码协议的强大工具。其能够承诺任意数据，表示为多项式，然后以安全、有效的方式验证该承诺，使其在区块链应用中非常有用。实际上，KZG 方案已在 EIP-4844 中得以利用，显著提高了 rollup 的效率。KZG 多项式承诺也是零知识证明协议（如 zkSNARKs）的基础组件，我们将在即将发表的文章中对此进行探讨。敬请关注！

如果你觉得这篇文章对你有所帮助，请关注我。这样会让我很开心，同时也会激励我创作更多优质文章。非常感谢你的支持 🙏

参考文献

1. 0xbarchitect — 高级加密原语
2. 0xbarchitect — Diffie-Hellman 问题
3. 0xbarchitect — BLS 签名方案
4. Aniket Kate, Gregory M. Zaverucha, and Ian Goldberg — Constant-Size Commitments to Polynomials and Their Applications
5. Dankrad Feist — KZG 多项式承诺
6. Wikipedia — 拉格朗日插值多项式
7. EIP-4844 — Blob-交易类型
8. Nguyen Thoi Minh Quan — 直观的高级密码学

• 原文链接： medium.com/@barchitect/k...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～