CAT与Schnorr技巧

作者：Andrew Poelstra

引言

这是关于在比特币中使用 Taproot 和（假设存在的）CAT 操作码实现 covenant 的一系列文章中的第一篇。历史上，以及在 Elements 中的实现，CAT 仅在结合 CHECKSIGFROMSTACK 时被视为 covenant 操作码。在这篇文章中，我们将讨论如何滥用 Schnorr 签名的数学特性来模拟 CHECKSIGFROMSTACK 的功能，这篇文章将比后续的文章更偏向数学。

首先，一些预备知识。Covenant 是一种假设的比特币脚本，它限制花费币的交易的形式。通常，脚本只能要求某些用于花费的认证数据的存在：签名、哈希锁检查等。脚本不能强制实施速度限制、将币限制到特定位置，或者类似的操作，因为脚本执行环境无法访问交易数据。最终，将 covenant 添加到比特币将意味着将交易自省的能力添加到脚本中。

其次，CAT 是“连接”操作码。它最初存在于比特币中，但 在 2010 年被悄悄移除，CAT 从堆栈中取出两个元素，将它们连接起来，并将结果推回堆栈。它可用于从小元素组装大堆栈项，或将大项拆分为小项。CHECKSIGFROMSTACK 从未在比特币中实现，它是一个允许用户检查任意数据上的签名的操作码，与 CHECKSIG 操作码不同，后者检查的是花费交易的签名。

CAT 和 CHECKSIGFROMSTACK 的组合以一种巧妙的方式提供了交易自省的功能：用户在堆栈上提供整个交易的数据；使用 CAT，脚本将所有数据捆绑成一个项，对其进行哈希并传递给 CHECKSIGFROMSTACK 以验证数据的签名。然后它将相同的签名与相同的密钥传递给 CHECKSIG。如果两次检查都通过，用户提供的交易数据必定是实际的交易数据。然后，使用脚本对这些数据进行 covenant 所需的任何检查就变得简单了。

ECDSA 和 Almost-Covenants

假设我们有 CHECKSIGFROMSTACK 但没有 CAT。那么原则上，我们可以实现一种非常简单的 covenant：用户提供所有交易数据的哈希，脚本通过 CHECKSIG 和 CHECKSIGFROMSTACK 检查签名的哈希。由于没有 CAT，脚本无法从可单独检查的数据重新计算哈希，所以它真正能做的就是将哈希与特定值进行相等性检查，这意味着币只能通过一个特定的交易花费。

可以很容易地将这种情况推广到少数交易的选项中，但开放式谓词如“任何输出小于 1 BTC 的交易”是不可能的。

事实证明，这种 covenant 无法正常工作，原因是：CHECKSIG 检查的交易数据总是包括前一笔交易的 txid，这是一个对（以及其他内容）covenant 脚本本身的哈希。（由于 SIGHASH_SINGLE 错误，这并不完全正确，但对我们的目的来说，这并没有帮助。）因此，脚本要生效，就需要包含它自己的哈希，这是不可能做到的。

这一观察的有趣之处在于，今天的比特币实际上有一种方法可以将交易哈希放到堆栈上，这意味着如果不是因为这个哈希循环问题，比特币今天就会有 covenant。如果有一种不包含前一笔交易数据的签名方法，例如使用在闪电网络世界中非常流行的 SIGHASH_NOINPUT 提案，比特币就会有 covenant。让我们看看这是如何工作的：

ECDSA 签名的生成如下：你有一个密钥对 ( x, P = xG)，分别表示签名和验证密钥。如果你不熟悉映射 x ↦ xG，它将标量（模某个大素数的整数）映射到椭圆曲线点（模另一个素数的整数对，满足特定方程）。重要的是：(a) 它是同态的，所以 ( x + y) G = xG + yG，(b) 除非使用量子计算机，否则被认为是不可能反向计算的。除了这两点，这个映射在算法层面上的样子并不重要；我们只将其视为一个黑盒。

为了生成 ECDSA 签名，你需要生成一个临时密钥对 ( k, R = kG)，然后计算值 r，它是点 R 的第一个分量，从模非标量素数强制转换为模标量素数的整数。（这个设计决策是由于法律原因做出的——对于专利目的来说，不可理解性算作新颖性，因此这个设计没有违反任何现有专利。）然后你计算值

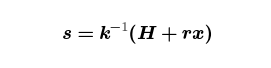
其中 H 是交易数据的哈希。让我们通过将两边乘以 k，然后通过 ⋅↦⋅ G ⋅ 映射来重新排列：

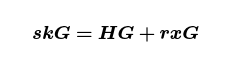
为了更清楚，可以写成

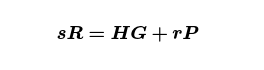
再重新排列一次，我们得到

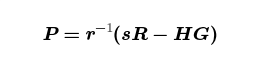
对于固定的 R 和 s，只要 H 是交易数据的哈希，这就是交易数据的加密哈希。实际上，比特币脚本有一个操作码用于“对于固定的 R 和 s，计算 H 并给我这样的 P”：CHECKSIG。

具体来说，考虑脚本 DUP <固定签名> SWAP CHECKSIGVERIFY。这只能在用户将满足条件的公钥 P 放在堆栈上时满足。脚本会复制它，将其与固定签名交换，然后在 <sig> <P> 上调用 CHECKSIGVERIFY。如果上述等式成立，这些将被消耗，留下 P 的副本在堆栈上。如果不成立，脚本失败，交易无效。

从这里可以学到两点：首先，在比特币中获得 covenant 真的很容易；其次，通过滥用数字签名的代数特性，可以使用签名检查操作码将交易数据放到堆栈上。

BIP340 签名和密钥前缀

Taproot 包含一种称为 BIP340 签名 的 Schnorr 签名变体。这些签名使用相同的密钥、相同的椭圆曲线和相同的标量群，但签名算法要简单得多：你像之前一样计算临时密钥 ( k, R = kG)，但这次

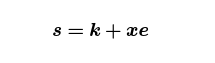
其中 e 是你的公钥 P、临时密钥 R 和交易数据的哈希。回想一下，我们无法从 ECDSA 获得 covenant 的原因是我们的脚本会最终进入交易数据，因此 P 的任何目标值都会最终出现在我们的消息哈希中，但由于 P 本身应该是哈希，我们就陷入了循环，无法继续。

看起来 BIP340 为这种 covenant 钉上了棺材钉：P 明确地出现在签名哈希中，所以无论比特币将来包含什么疯狂的签名方案，这种循环性都会持续存在，我们会陷入困境。事实上，P 的包含意味着 BIP340 签名不仅仅是签名，而是“知识签名”。这是一个术语，大致意思是你在任何意义上都无法反向运行这些签名。很长一段时间以来，我认为这意味着我无法滥用 BIP340 签名以获取非签名的行为。

事实上，我错了，尽管我需要 CAT 来获得真正有趣的行为。诀窍在于，虽然我无法通过固定 s 和 R 来从 P 中获取交易哈希，但我可以固定 R 和 P 来从 s 中获取交易哈希。事实上，生成的交易哈希是一个“真正的”哈希，因为其中没有涉及脚本无法处理的椭圆曲线操作。

具体来说，考虑脚本 2DUP CAT ROT DUP <G> EQUALVERIFY CHECKSIG。这个脚本

• 将签名作为输入，分成两部分，所以我们的堆栈是 R s；
• 2DUP CAT 复制这两部分并将副本连接起来，堆栈变为 R s Rs；
• ROT DUP 将 R 移到堆栈顶部并复制，堆栈变为 s Rs R R；
• <G> EQUALVERIFY 消耗顶部的 R 并强制它们都成为椭圆曲线群生成器 G；
• CHECKSIG 将剩余的 R 解释为公钥，并验证签名 Rs，消耗两者；
• 现在只有 s 在堆栈上。

哇。这到底是在干什么？好吧，我们强制 R 和 P 成为群生成器的步骤相当于强制我们的秘密密钥 x 和 k 为 1。我们的 BIP340 签名方程变为

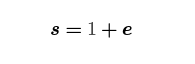
即我们的脚本留在堆栈上的 s，实际上是我们的交易数据的 SHA256 哈希，前缀是 G 的几份副本（以及几份 SHA256("BIP0340") 的副本，因为 BIP340 非常自恋）。非常有趣。脚本有一个操作码 SHA256，在我们假设的世界里有 CAT，所以如果我们可以以某种方式处理这个 +1，我们将能够让用户提供交易数据，我们可以对这些数据进行约束，然后验证其哈希，就像我们有 CHECKSIGFROMSTACK 一样。

事实上，这个 +1 很容易处理。我们只需要让用户对她的交易数据进行穷举，直到实际哈希以字节 01 结尾，这是相当便宜的（平均需要 256 次尝试，每次尝试 250 纳秒，总共需要 64 微秒，与签名算法本身相当）。那么她的 s 值将以 2 结尾，我们通过要求她去掉它来强制执行；我们自己会添加它。具体来说，在我们计算 s 的脚本中，在 2DUP 后添加一个 2 CAT，并在我们希望结果成为我们的交易哈希的脚本末尾添加 1 CAT。完成了。

接下来的步骤

这是一次奇妙的旅程：事实证明，Taproot 中的 BIP340 签名虽然设计得比老派的 ECDSA 签名更“防范 covenant”，但实际上让我们更接近 covenant。事实上，我们只需要 CAT 就能获得 CAT + CHECKSIGFROMSTACK 风格的 covenant。

然而，如果我们希望构建递归 covenant，动态限制交易输出脚本遵循某些模板，这就会成为一个问题。在 Taproot 中，交易输出是椭圆曲线公钥，它们使用我们没有在脚本中实现的椭圆曲线哈希来提交脚本。……还是我们有？

我认为答案是否定的，但我也认为，我们仍然可以用它做一些非常有趣的事情。

一个自然的问题是，鉴于脚本的共识限制，这些签名哈希模板化 covenant 是否真的足以做任何事情？读者可能还记得我们 四年前在 Blockstream 博客上写过 相关的内容，但没有进一步跟进实际应用。现在我的观点是，应用的贫乏更多地是由于构建和推理脚本的极端困难，而 Miniscript 为此提供了一些新的思考方式，将加速这种发展。事实上，如果你真的想深入研究脚本，你可以用 CHECKSIGFROMSTACK 构建一些非常酷的东西。

在我们的下一篇文章中，我们将讨论如何使用辅助输入来模拟 SIGHASH_NOINPUT 并实现闪电网络的恒定大小备份，以及如何使用“值切换”来构建保险库。

在我们的最后一篇文章中，我们将讨论 Miniscript 的临时扩展，以及如何以可维护的方式为这些结构开发软件。

本文最初发布于 https://www.wpsoftware.net/andrew/blog/cat-and-schnorr-tricks-i.html

• 原文链接： medium.com/blockstream/c...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～