什么是FM-AMM，CoW AMM背后的理论，以及它是如何抵御MEV攻击的？

  • EthTaipei
  • 发布于 2024-11-22 18:45
  • 阅读 136

本文探讨了功能最大化自动做市商(FM-AMM)设计，强调其在去中心化金融(DeFi)中的创新特点。通过对比常量函数自动做市商(CFAMM)，FM-AMM的独特批处理机制和双价格影响使其抵御了最大可提取价值(MEV)攻击。实验结果显示，FM-AMM在高流动性交易对中表现良好，但在低流动性交易对中表现不佳，本文还讨论了其潜在的应用前景和需要进一步优化的方面。

揭开 套利者的利润、LVR 及三明治攻击：批量交易作为 AMM 设计响应

《奶牛》，文森特·梵高。图片来源：https://en.wikipedia.org/wiki/The_Cows_(painting)

编辑注：

在今天的 AMM 中，交易的平均价格与 AMM 的交易后价格之间的差异为套利者通过 MEV 攻击创造了利润机会。FM-AMM 提出了一个深刻的问题：如果这两个价格对齐，是否可以消除这些套利机会？本文将分解 FM-AMM 的设计，探讨其独特的批量机制和双重价格影响如何使 AMM 抵御 MEV。

作者：Yuren，来自 Perpetual Protocol 的我的朋友 😁

目录

  1. tl;dr
  2. 介绍
  3. CFAMM 上的 MEV
  4. 使用常数函数推导 FM-AMM
    1. 双重价格影响
    2. 类似于 CFAMM，交易后增加流动性
    3. 一个具有可定制权重的自动再平衡两资产组合
  5. 批量交易的必要性
  6. 实验结果
    1. 与同一费率层的 Uniswap V3 比较
    2. 最优费率层
  7. 两个小限制
  8. 前景
  9. 结论

0. tl;dr

  • FM-AMM 通过清算价格一致性解决 MEV，其中交易的平均价格等于边际价格。
  • 流动性储备的常数是 FM-AMM 旨在最大化的函数。
  • FM-AMM 与 CFAMM 之间的主要区别在于批量交易。
  • FM-AMM 的价格影响是 CFAMM 的两倍。
  • FM-AMM 作为一个具有可定制权重的自动再平衡两资产组合，类似于 CFAMM。
  • 实验表明，FM-AMM 在高交易对上表现优于低交易对。虽然 0 费率层看起来很有前景，但可能需要进一步研究来确定 FM-AMM 的最优费率层。

1. 介绍

CoW AMM 的公告及其在 Balancer 上的实施已经发布超过六个月，但有关其创新、理论和设计的讨论却很少。

CoW AMM 现已在 Balancer 上运行：https://balancer.fi/pools/cow

起初，我认为缺乏兴趣可能源于一个简单的事实：也许这里没有太多的创新，它只是另一个常数函数 AMM (CFAMM) 的实现。

显然，我错了，这引出了本文。🙈

在对这一主题进行研究并开始草拟我对 CoW AMM 的看法时，我最终探讨了 CoW 团队频繁引用的关键论文：套利者的利润、LVR 及三明治攻击：批量交易作为 AMM 设计响应，作者：Andrea Canidio & Robin Fritsch。

在这篇论文中，我发现功能最大化 AMM 确实提出了 MEV 的一个明确数学解决方案。因此，让我们探索这一引人注目的 DeFi 新概念：功能最大化 AMM，FM-AMM。

顺便说一句，我喜欢在做数学时听音乐；还有其他人吗？

mac ova seas - 闪电 (feat. 李佳隆) [官方歌词视频]

FirePanda

2. FM-AMM 及其 MEV 抵抗性

功能最大化 AMM，顾名思义，旨在最大化一个函数，在本文中，这个函数被定义为 AMM 的流动性储备。

例如，如果一个 FM-AMM 最初构建为常数函数，类似于一个常数函数 AMM (CFAMM)，那么两个流动性储备的乘积 X * Y = K 就成为其最大化目标。

本文介绍了一种新颖的 AMM 机制，旨在抵御 MEV。正如我们将进一步探讨的，这种设计中固有的曲线移动行为激励了 FM-AMM 这个名称。

在我们正式开始之前，有两个重要的背景知识需要了解：

  • CFAMM：CFAMM 促进在曲线 X × Y= K 上始终发生的交易，其中 X 和 Y 表示两种不同代币的数量，K 是一个常数。了解更多：Uniswap V3 功能详细解释#1. Uniswap 与 AMM 回顾。
  • MEV：最大可提取价值是矿工或验证者通过安排区块中交易以他们的优势获取的利润，例如，将自己的交易放在其他交易之前以获得更好的价格。

现在，让我们直接深入到理解本文的最关键问题：我们如何在数学上定义 MEV，特别是在 CFAMM 曲线上？

本文将 CFAMM 上的 MEV 定义为以下两者之间的价格差异：

  1. 交易的平均价格，以及
  2. 交易后交易一个几乎为零的小额（几乎为零）代币的价格。在本文中，这被定义为“边际价格”。

简单来说，假设我们在 CFAMM X * Y = K 上交易 x’，则 X 当前价格为 P0 = Y / X。关于价格的分析如下：

交易 x’ 的平均价格 P1

  1. Y * X = (Y + y')(X − x')，其中 y’ 是 Y 的变化
  2. 由于 y’ = p1 * x'，故 (Y + y')(X − x') 变为 (Y + P1 * x')(X − x')
  3. 现在我们有 Y * X = (Y + P1 * x')(X − x')，解 P1 得到：P1 = Y / (X - x')

交易 x’ 后的边际价格 P2

  1. 在交易后，新常数为(Y + P1 * x')(X − x')
  2. 假设交易一个非常小的数量对结果的影响可以忽略，价格 P2 变为：P2 = (Y + P1 * x') / (X − x')

示例

  • 设 X = 1（1 ETH）
  • Y = 1000（1000 USDC）
  • x’ = 0.4（交易 0.4 ETH；在现实中，交易流动性储备的 40% 并不明智）

计算

  • P0 = Y / X = 1000 / 1 = 1000，1 ETH 的价格为 1000 USDC
  • P1 = Y / (X - x') = 1000 / (1 - 0.4) ~= 1666
  • P2 = (Y + P1 * x') / (X − x') = (1000 + 1666 * 0.4) / (0.6) = 2777

我们可以观察到明显的价格差异：交易的平均价格 (P1) 低于交易后 AMM 池的新价格 (P2)，这为 MEV 创造了机会。

如果套利者可以访问更具流动性的交易所，可能是中心化的，他们可以以小滑点在市场价格上出售代币，他们便可以以较低的平均价格从 AMM 购买代币并从差价中获利。

例如，考虑一个场景，其市场价格从 1000 USDC/ETH 转变为 2777。如果套利者以平均价格 1666 USDC 在 AMM 上购买 0.4 ETH，并成功在更具流动性的市场以 2777 USDC 出售，他们可以获得利润 0.4 * (2777 - 1666) = 444.4 USDC。

3. 使用常数函数推导 FM-AMM

对于熟悉方程的人来说，它们的出现可能暗示着有些有趣的东西可以揭示！ 🥳

如果 MEV 被定义为价格差异，那么让两者的价格相同是否能有效解决 MEV 呢？

在论文中，使 FM-AMM 抵御 MEV 的关键特性是“清算价格一致性”，这意味着平均交易价格与边际价格相匹配。我们来分解实现这一点所需的条件：

P1 = (Y + P1 * x') / (X − x') = P2

-> (Y + P1 * x') = P1 * (X  − x')

-> Y + P1 * x' = P1 * X - P1 * x'

-> Y = P1 * (X - 2 * x')

-> P1 = Y / (X - 2 * x') = P2

瞧！当平均交易价格为 Y / (X − 2 * x’) 时，它也成为交易后的边际价格。

建立了 FM-AMM 的第一个条件后，我们可以从中得出几个有趣的观察结果！

1. 双重价格影响

如果我们将 FM-AMM 的平均价格 Y / (X − 2 * x’) 与典型 CFAMM 的平均价格 Y / (X - x') 进行比较，我们会注意到 x’ 的倍增效应是双重的。这表明 FM-AMM 的价格影响是 CFAMM 的两倍。

2. 类似于 CFAMM 交易后增加流动性

由于 FM-AMM 的平均价格与 CFAMM 的平均价格不同，因此它们的交易后常数也不能相同：

Y' * X' = (Y + P1 * x') * (X − x')

= (Y + Y * x' / (X − 2 * x')) * (X − x')

= Y * ( 1 + x' / (X − 2 * x')) * (X − x')

= Y * ((X − 2 * x' + x') / (X − 2 * x')) * (X − x')

= (Y * ((X - x') / (X − 2 * x'))) * (X − x') = Y' * X'

虽然 X’，新的 X 储备保持不变 (X - x’)，Y’ 变为 Y * ((X - x’) / (X − 2 * x’))。由于 Y 的分子 (X - x’) 大于分母 (X − 2 * x’)，因此乘数大于 1，使得 Y’ 大于 Y。

这意味着曲线向上移动，增加了 Y 储备。我们可以用上面的例子进行可视化，x’ = 0.4, X = 1, Y = 1000：

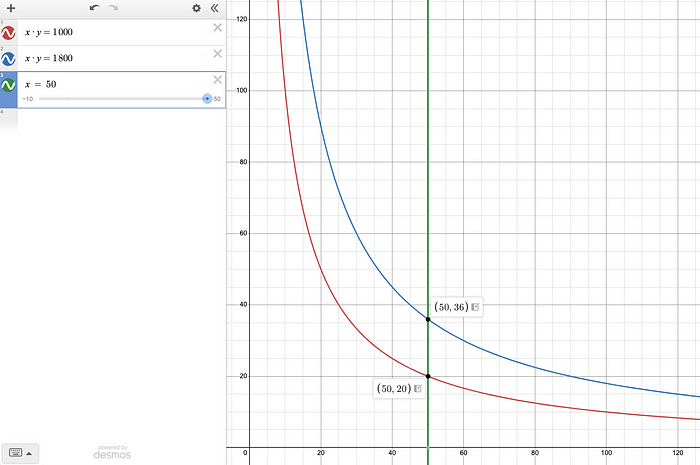
亲自探索这个互动图： https://www.desmos.com/calculator/deeekfzima。绿色线只是为了显示曲线的移动。

通过遵循清算价格一致性的特性，蓝色的 FM-AMM 曲线从红色的 CFAMM 曲线 X * Y = 1000 向上移动到 X * Y = 1800 = 1000 * 0.6 / 0.2 * 0.6。

由于向上或向右移动曲线表示流动性增加，因此这一行为强调了 FM-AMM 从根本上是一个优化/最大化问题。¹

然而，如果你熟悉 Uniswap V1 和 V2²，你可能已经在想着：Uniswap V1 和 V2 的曲线在每次交易后也会由于费用被添加到池中而发生移动？

你说得对！ FM-AMM 是对 CFAMM 的一个近似，在每次交易后增加额外的流动性。在数学中，近似意味着陈述并不是完全准确，但在某些条件下足够接近以发挥作用。

换句话说，FM-AMM 的行为与 CFAMM 类似，都是在交易后由于增加的流动性而经历曲线移动。

¹请注意，CoW AMM 的实现强调通过接受带有最大盈余/曲线移动的批量解决方案实现最大化，而不是强制平均价格 == 边际价格。

²Uniswap V3 的区间分割防止在每次交易后将费用添加回流动池。

3. 一个具有可定制权重的自动再平衡两资产组合

如果我们查看新 X 储备 X’ = (X - x’) 与其价格 P1 的乘积，我们会发现两个储备具有相等的价值：

P1 (= P2) * (X - x')

= Y / (X − 2 * x') * (X - x')

= Y * (X - x') / (X − 2 * x') = Y'

在得出明显结论之前，让我们将此观察与 FM-AMM 的交易后常数连接起来：(Y + P1 * x')(X − x')。请注意两个资产的值保持一致，并相等地为常数做出贡献——这是因为每个储备在方程中具有相等的指数：

(Y + P1 * x')(X − x') = (Y + P1 * x')^1 * (X − x')^1

由此我们可以得出结论，FM-AMM 可以通过实现相应的加权函数 (Y + P1 * x')^α * (X − x')^(1-α) 来表示任意权重的任意策略（α，1-α），这自然涵盖了两种资产权重和值相等的情况。

请注意，这一属性与 CFAMM 相同。如果我们将新的储备 X (X - x’) 乘以交易后的价格 P2 (Y + P1 * x') / (X − x')，那么它变成了 (Y + P1 * x') / (X − x') * (X − x') = Y’，这仍然是 Y 的新储备。

4. 批量交易的必要性

这一部分可能对像我这样的数学非专业人士来说是最具挑战性的，但我们快到了——这是涉及数学的最后一部分。 🥳

为了理解为什么批量交易对 FM-AMM 是必要的，我们还引入 DeFi 中的这些常见概念：路径依赖和独立性。

在 AMM 的背景下，路径依赖/独立性意味着最终结果或状态取决/不取决于交易的顺序。

CFAMM 是路径无关的，因为 AMM 达到的最终价格不依赖于交易的顺序。例如，在我们的场景中，x’ = 0.4, X = 1, Y = 1000，最终的边际价格将始终达到 2777，无论交易是在一个步骤中执行还是分成多个较小的交易。

相比之下，FM-AMM 是路径相关的，这需要稍微更复杂的数学分析。

  1. 回顾交易后的常数 X’ 和 Y’ 分别为 X − x’ 和 Y * ((X - x’) / (X − 2 * x’))。
  2. 如果我们将交易分为 n 个较小部分，使得 ∑(i=1~n)xi = x'，则 FM-AMM 的储备将变为 X - ∑(i=1~n)xi 和 Y * ∏(i=1~n)( (X - ∑(j=1~n-1)xj) - xi) / (X - ∑(j=1~n-1)xj) - 2 * xi) )，其中 ∑ 是在给定范围内的所有值的总和，而 ∏ 是所有值相乘的乘积。
  3. 假设 xi = 1/n * x'，意味着每个 xi 是 x' 的平等 1/n 部分。这一步有效地消除变量 i 对 x'/n 的影响：∑(i=1~n) x'/n，也就是说结果只是 x/n 乘以总和 n 的迭代次数：x'/n * n = x'。因此，X 的储备保持为 X - x'。
  4. 我们还可以应用 xi = x'/n 到 Y 储备，以消除 i 和 j：Y * ∏(i=1~n)((X - x'/n * (i-1)) - x'/n) / (X - x'/n * (i-1)) - 2 * x'/n) )。由于 (X - x'/n * (i-1)) - x'/n) = (X - i*x'/n) 和 (X - x'/n * (i-1)) - 2 * x'/n) = (X - (i+1)*x'/n)，因此该表达式变为 Y * ∏(i=1~n)((X - i*x'/n) / (X - (i+1)*x'/n))
  5. 下一步可能看起来很棘手，这涉及到识别乘积序列的行为：∏ 表示序列中每个值的乘积。通过展开乘积，我们可以看到所有乘积相互抵消：∏(i=1~n)((X - i*x'/n) / (X - (i+1)*x'/n)) = (X - 1*x'/n) / (X - 2*x'/n)) * (X - 2*x'/n) / (X - 3*x'/n)) * (X - 3*x'/n) / (X - 4*x'/n)) ... * (X - n*x'/n) / (X - (n+1)*x'/n))，最终仅留下 (X - 1*x'/n) / (X - (n+1)*x'/n))
  6. 现在，让我们设想将交易分为无穷小的部分。这个过程被称为 lim n→∞，模拟随着 n 接近无穷大时的极端结果：lim n→∞ Y * (X - 1*x'/n) / (X - (n+1)*x'/n))。由于 n 出现在分母中，随着 n → ∞，x'/n 接近 0。同时，项 (n+1)/n 接近 1。最终，该表达式简化为 Y * X / (X - x')，这与 CFAMM 的 Y 交易后储备相匹配！

上述推导表明，如果将交易分割为许多个较小的交易，FM-AMM 将退化为 CFAMM，有效地证明了将交易批量到一个 tx 里的必要性，这是 CoW AMM 的基础。

为了加深理解，让我们继续应用一些数字来观察批量对两个储备的最终乘积的影响，计算为 (Y * ((X - x’) / (X − 2 * x’))) * (X − x’)。我们将使用相同的设置，X = 1, Y = 1000，并比较一笔交易 x’ = 0.4 与将其分割为两笔 x’ = 0.2 交易的情况：

  • 一笔交易（批量）：(1000 * ((1 - 0.4) / (1 − 2 * 0.4))) * (1 − 0.4) = 1800
  • 两笔交易（无批量）。第一笔交易：(1000 * ((1 - 0.2) / (1 − 2 * 0.2))) * (1 − 0.2) ~= 1066，第二笔交易：(1333 * ((0.8 - 0.2) / (0.8 − 2 * 0.2))) * (0.8 − 0.2) = 1199*

批量的效果显而易见且显著！

*第一次交易后的 Y 储备为 (1000 * ((1 - 0.2) / (1 − 2 * 0.2))) = 1333

5. 实验结果

虽然论文深入探讨了费用对 FM-AMM 的影响，但我将直接关注实验结果：

1. 与同一费率层的 Uniswap V3 比较

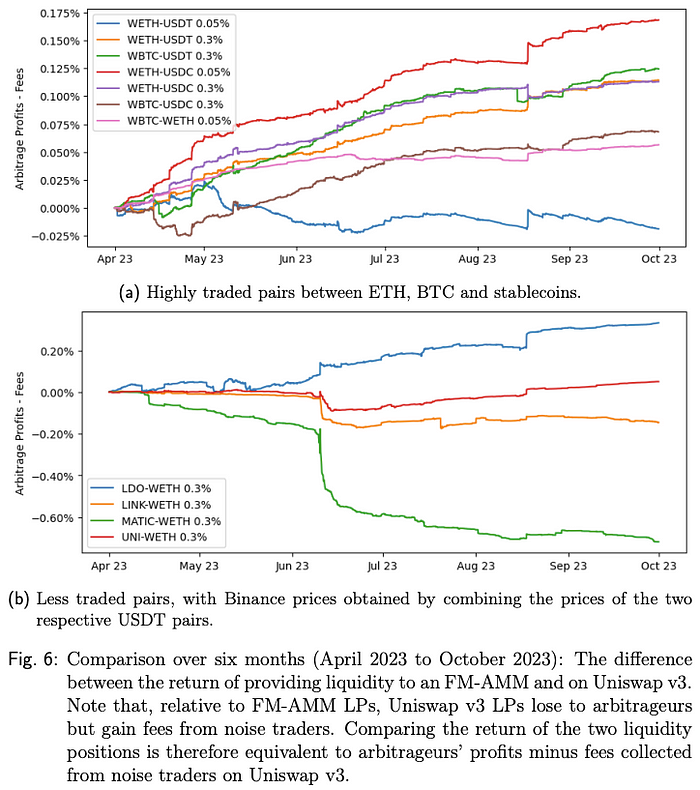
图片来源：套利者的利润、LVR 及三明治攻击：批量交易作为 AMM 设计响应

论文模拟了被动流动性提供——无需主动流动性管理——在 FM-AMM 上使用与其对应的 Uniswap V3 池相同的费率层。结果表明，在高交易对上提供流动性一般优于低交易对。

2. 最优费率层

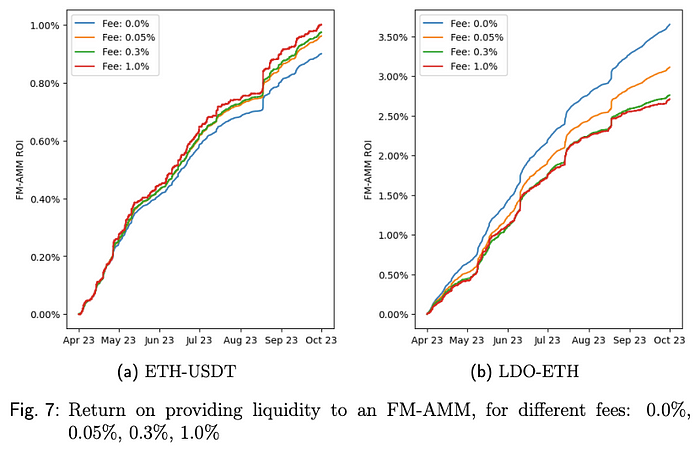
图片来源：套利者的利润、LVR 及三明治攻击：批量交易作为 AMM 设计响应

在论文中分析了 6 个池：其中 4 个 0 费率池表现优秀，而其余两个由 0.1% 费率层引领。至于表现最差的池，0 费率、0.1% 和 0.3% 层各占 2 个实例。值得注意的是，6 个样本不足以提供统计学意义，所以我很好奇作者是否进行了进一步分析，因为这些信息将是非常有价值的！

6. 两个小限制

关于 FM-AMM，我有两个小限制想说：

  • 如前所述，Uniswap V3 的范围分割防止再次将费用添加到池中，使得不太可能构建类似于 Uniswap V3 的 FM-AMM。然而，考虑到关于 LP 在 Uniswap V3 上的盈利能力的持续讨论，这并不一定是一个缺陷 😹。
  • 虽然批量的好处可能不稳定，但它们仍可产生正总和。例如，如果多个方向的交易互相抵消，这些交易可以 P2P 地结算，这不会要求 AMM 调整其在曲线上的位置或最大化其流动性储备函数——除非 P2P 结算的费用仍被添加到池中。

7. 前景

虽然可能需要进一步研究以优化 FM-AMM 的设计，例如最优费率层，但 FM-AMM 可能带来一些激动人心的可预见变化：

  • FM-AMM 的自动再平衡特性、抵御 MEV 和可定制权重，对需要再平衡的金融产品看起来很有前景，可能会影响金融的许多方面，例如 ETF。
  • 如果批量本质上是 FM-AMM 和 CFAMM 之间的主要区别，例如 Uniswap V1 和 V2，而 UniswapX 正在成为流动性聚合器……🤔
  • FM-AMM 可以实现两种加权资产。那么多加权的资产呢？FM-AMM 能否扩展到多资产常数函数？这就是 CoW AMM 构建在 Balancer 上的原因吗？🤩

你能想到更多有趣和激动人心的想法吗？请随时分享！

8. 结论

展开所有数学是令人疲惫的 🫠🫠🫠

我希望这篇文章能帮助所有耐心的读者更好地理解这个神秘而大多处于低调的 FM-AMM 的细节。我对 FM-AMM 的坚实数学基础感到愉悦，这清晰地为抵御 MEV 的 AMM 开辟了道路，同时也激励我撰写这篇文章！

像往常一样，请指出你发现的任何错误，欢迎在下面留下你的评论和想法。现在我真的需要小睡一会和放松一下 🥱 🥦 🛋️

感谢 Andrea、Yuren 和 Anton 的评审和反馈！ 🙏🙏🙏

  • 原文链接： medium.com/taipei-ethere...
  • 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
EthTaipei
EthTaipei
Taipei Ethereum Meetup

EthTaipei

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！