在 RISC Zero 中验证全同态加密 (FHE)，第二部分

在我们之前的文章中，我们深入探讨了在 RISC Zero 中全同态加密 (FHE) 的引导步骤验证。基于这一基础，本文将重点转向性能优化。

当人们在 RISC Zero 中进行优化时，最重要的教训是 仅关注主要瓶颈。要知道瓶颈所在，我门可以通过了解程序中每一部分对“ZK 证明”开销的贡献来对程序进行分析。

本文致力于通过结合 理论 和 实验 找出这一证明开销，重点关注 RISC Zero。

ZK 证明开销的影响因素

让我们从理论谈起。在 RISC Zero 中，“ZK 证明”开销的数量是以“周期（cycles）”来衡量的。这本质上类似于 CPU 的周期。和普通的 RISC-V CPU 一样，RISC Zero 的周期主要来源于两个方面： 计算和分页。

计算。 每个 RISC-V 指令在执行时，会在 RISC Zero 中产生一定的 CPU 计算周期，如下所示，基于 开发者文档。

• 一个周期： LUI, AUIPC, JAL, JALR, BEQ, BNE, BLT, BGE, BLTU, BGEU, LB, LH, LW, LBU, LHU, SB, SH, SW, ADDI, SLTI, SLTIU, SLLI, ADD, SUB, SLL, SLTU, MUL, MULH, MULHSU, MULHU

• 两个周期： XORI, ORI, ANDI, SRLI, SRAI, XOR, SRL, SRA, OR, AND, DIV, DIVU, REM, REMU

• 每 64 个字节 76 周期： SHA-256 的系统调用

• 10 周期： 256 位模乘的系统调用

大多数常用指令（例如对 32 位数字进行加法和乘法的指令）产生一个周期。一些位操作和除法涉及两个周期。系统调用会调用加密加速器，会需要更多的周期。这在本质上类似于现代 CPU 的 SHA 扩展，它增加了仅需几个周期就能执行的专用指令，专门用于 SHA256。

需要注意的是，RISC Zero 的周期计数是特定于 RISC Zero 的——现实世界中的 RISC-V CPU 芯片几乎保证会有不同的周期计数，因为计算成本通常高于验证成本。未来版本的 RISC Zero 可能对于每条指令具有不同的周期计数。

然而，由于分页，一条指令也可能产生非计算周期，这也可能是一个重要的开销来源。

分页。 为了理解 RISC Zero 中分页的开销，首先回顾一下现代 CPU 如何根据数据存储位置来处理数据访问是有用的。

• 在 L1/L2 缓存中：数据存取可以在几个周期内完成。

• 在主内存中：数据访问的延迟为数百个周期。

• 在外部存储中：数据需要首先加载到主内存中——称为“页内存”，在此期间 CPU 需要等待，即使外部存储是高端 SSD，这一过程也可能需要超过数万个周期。数据可能还需要从主内存“页出”到外部存储中。

我们称之为“页内存”和“页出”，因为现代操作系统将程序可以访问的内存组织为“页面”。页面大小因平台而异。在配备 M2 芯片的 Mac Studio 中，每个页面为 16KB。RISC-V 标准使用 4KB。在 RISC Zero 中，页面更小，每个页面为 1KB。

在 RISC Zero 中，程序可以使用最高约 192 MB 的空间，地址范围从 0x0400 到 0x0c000000。该空间被划分为每个 1KB 的页面。这些页面通过多个页表进行索引，大约占用 6.7MB 的空间，位于从 0x0d000000 开始的区域。与现代操作系统类似，页表是 多级，如图 1 所示。

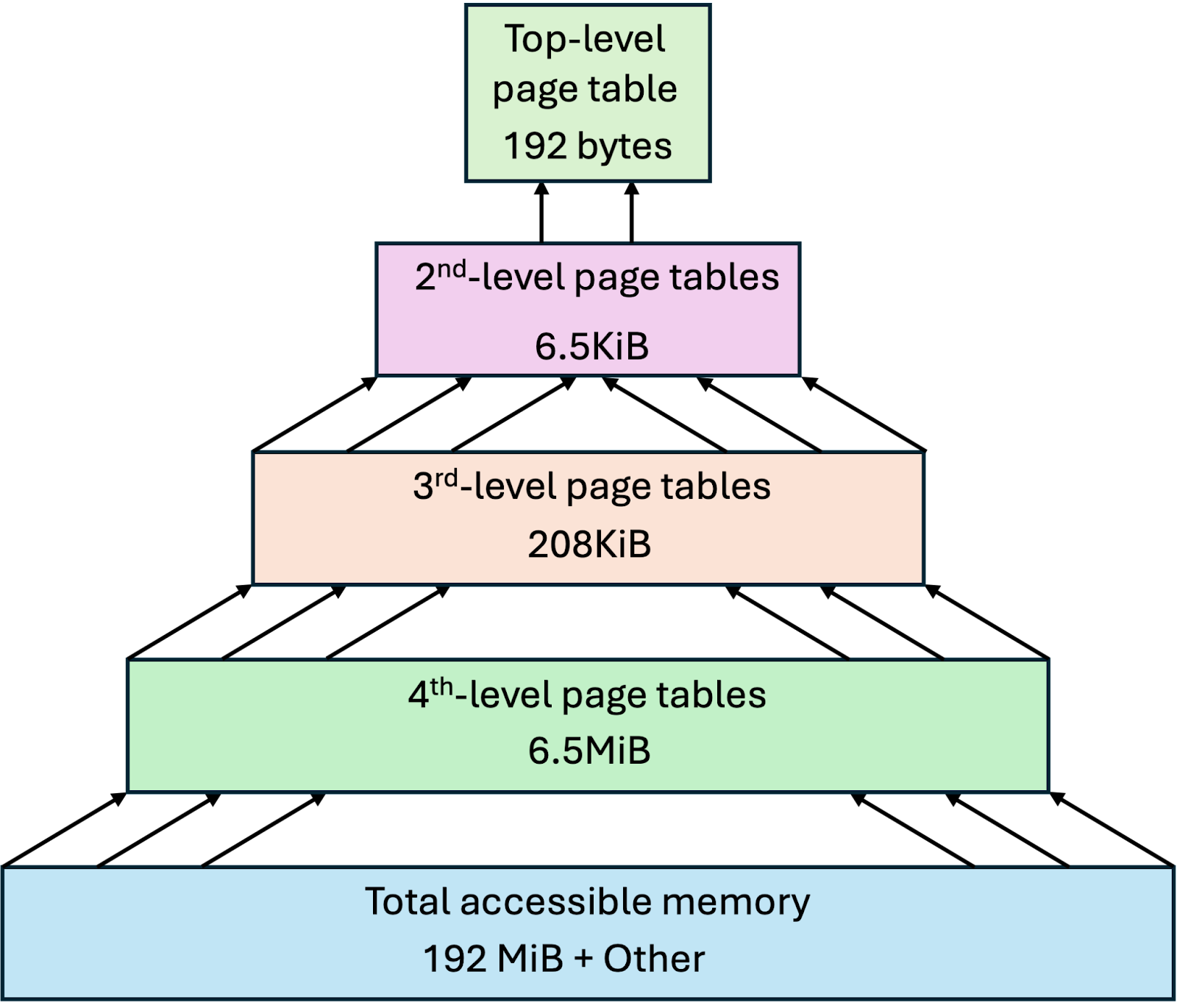
图 1：RISC Zero 中来宾程序内存空间的多级页表。

在 RISC Zero 程序中，当一个页面首次被访问时，RISC Zero 需要 “zk-load” 该页面，以便将其数据放入 ZK 电路可以使用的经过认证的格式。在执行结束时，RISC Zero 将 “zk-unload” 该页面，以验证该页面是否已以与 ZK 电路执行一致的方式被修改。

注意，要加载或卸载一个页面，RISC Zero 需要加载或卸载其页表。换句话说，整个程序的第一条指令将加载 5 个页面：

• 页面 A： 指令所在的页面。

• 页面 B： 页面 A 的第四级页表。

• 页面 C： 页面 B 的三级页表。

• 页面 D： 页面 C 的二级页表。

• 页面 E： 顶级页表。

每次页面加载/卸载贡献约 1094 周期，唯一例外是顶级页表，需 754 周期，略少。这可以通过我们即将介绍的一个工具进行可视化，允许我们查看在整个执行过程中加载或卸载的页面数量是如何变化的。

图 2：来自 GDB for RISC Zero 的输出示例，说明周期。

对于在 RISC Zero 中运行的 RISC-V 程序，页面周期的数量因此取决于在整个执行过程中访问或修改的内存页面的数量——人们也称之为“ 内存足迹”。可以看出，从优化的角度看，有必要避免在特定时刻使用过多的内存。换句话说，RISC Zero 更倾向于降低峰值内存。

现在我们谈到了周期，接下来想解释周期为何与 ZK 证明开销直接相关。这与 RISC Zero 如何执行零知识证明有关。有关 RISC Zero 的 ZK 电路文档不多，但代码是开源的。为了理解 ZK 证明开销，我们先来了解一下 RISC Zero 的 ZK。

从周期到 ZK 证明

简而言之，RISC Zero 的证明系统可以总结如下。

• UltraPlonk（或 Halo2）。算术化由自定义门、高度多项式关系、多个见证线和查找参数组成。

• FRI。使用快速的 Reed-Solomon 交互式接近证明进行多项式评估和承诺（就叫它 FRI）。

• BabyBear。计算在 BabyBear 域（模数为 15 * 2^27 + 1）上定义，代数全息证明期间使用四次扩展。在 BabyBear 元素中存储一个字节的数据。换句话说，一个 32 位整数使用四个 BabyBear 元素。

• 内存检查。尽管页面是使用 Merkle 树进行认证的，但主内存使用一种代数内存检查技术，因此对主内存的每次访问总是只会产生常量开销。

• 来自 Groth16 的 SHARK。证明生成将生成可以进一步压缩的 STARK 证明——在不泄露信息且以无信任的方式下——转换为非常简洁的 SNARK 证明，通过 Groth16 进行。我们预计 RISC Zero 将在隐私缩放探索 (PSE) 的 公共仪式平台 上进行 他们的设置仪式，P0tion。

RISC Zero 的完整电路是开放的，但将高层描述转换为电路的编译器 Zirgen 还未发布。尽管如此，一些来自 Nethermind 和 RISC Zero 的视频应该能够让你对电路的来源有一个大致的了解，以及为什么需要编译器以实现高效、硬件无关性和形式验证。

请注意，上述 RISC Zero 证明系统的摘要仅适用于今天的状况。未来可能会有很大不同。随着 RISC Zero 递归（先前称为“ 续期”，但现在更具泛化性）的发展，RISC Zero 可能会成为某种“Plonk”，人们可以自定义自己的特定应用变体的 RISC Zero，以适应不同的应用。

人们可以想象一个未来，RISC Zero 成为不同 ZK 协议的中心，就像 Minecraft 拥有一个非常庞大的 modding/plugins 生态系统，包含 150k+ 个社区项目。在这里，RISC Zero 提供通用支持和一般特性——就 RISC-V 和 SHA256/BigInt 系统调用而言——以及用于电路生成的基础设施（Zirgen），远程证明委托和压缩（Bonsai），同时还为不同的后端提供高效实现，包括 CPU、Metal 和 CUDA，这些都是由 Zirgen 推导而来。来自其他目标平台的可执行文件——比如 WASM——可以通过即时编译（ JIT）转换为 RISC-V，而无需太多 VM 开销，这类似于 Solana 的 JIT 机制—— rbpf。

图 3：基于 RISC Zero 构建的证明系统的潜在未来。

此前，人们在“自制加密”过程中面临的两个最大挑战是 (1) 创建证明系统的技术和知识障碍 (2) 对安全性的信心不足。值得庆幸的是，Zirgen 有助于解决第一个问题，而 Nethermind 也讨论过如何促进形式验证。一个社区自制的、形式上经过验证的、专为普通人构建的特定应用证明系统——可能有 GPT 的帮助——不再遥远，这可能是真正的 ZK 证明系统去“精英化”的去中心化。

在 RISC Zero 中，有大约六个 ZK 电路，编码 RISC-V 程序执行的限制条件，每个电路大小不同，具体如下。

• 一个电路验证最多 32768 (=2^15) 周期的执行

• 一个电路验证最多 65536 (=2^16) 周期的执行

• 一个电路验证最多 131072 (=2^17) 周期的执行

• 一个电路验证最多 262144 (=2^18) 周期的执行

• 一个电路验证最多 524288 (=2^19) 周期的执行

• 一个电路验证最多 1048576 (=2^20) 周期的执行

为了为特定的 RISC-V 程序选择电路，RISC Zero 首先运行程序，找到完成所需的周期数。接着，选择出能处理该周期数的最小电路。如果执行超过 2^20 周期，则整个执行将被拆分成每个最多 2^20 周期的段，这些段的证明通过证明递归合并在一起。

所有这些电路遵循一个相当简单的结构。

• 预加载子电路： 验证执行环境的初始化——字节形式性检查和 RAM 的查找表初始化、初始数据加载到 RAM，并且，最后且重要的是，禁用预加载特权。这类似于 x86-64 中的“ 实模式”，其中引导程序在特权模式下运行，随后切换到“ 保护模式”以进行实际操作系统，特权被剥夺。这个子电路占用约 ~1592 周期的电路空间。

• 主体子电路： 验证在后续 ~ 2^k - N{pre} - N{post} 周期内每个周期是否符合 RISC-V CPU 的行为。这个电路高度重复，因为这里的每个周期都是相同的。注意页面加载和卸载都在主体中进行。这类似于操作系统处理虚拟内存和页面管理。

• 后加载子电路： 验证计算是否正确结束，并关闭字节形式性检查和 RAM 的查找表。这个子电路正好放在电路的末尾，占用的电路空间约为 N_{post} = ~6 周期。人们可以想象这就像机器自身关闭电源。

在 RISC Zero 的 GitHub 仓库中，可以在 这里 找到主体子电路的定义。

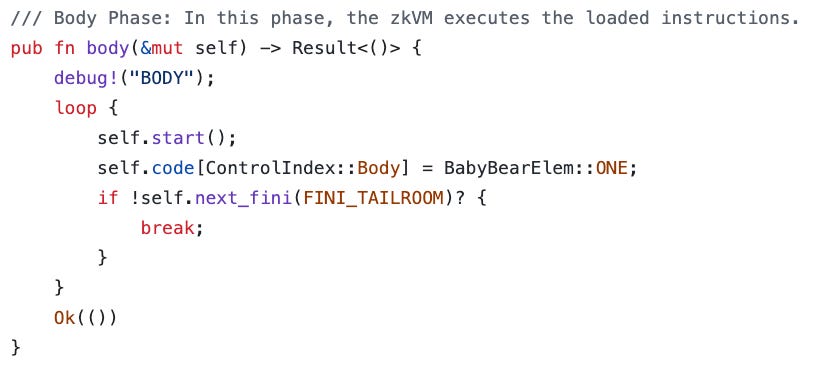
图 4：zkVM 主体阶段约束系统的构建。

正如你所见，主体子电路非常简单，只是不断向底层 ZK 电路的主体线写入“1”，直到是时候进行后加载。

像其他 FRI 证明系统一样，由于 FRI 不关心电路是否稀疏或密集，证明生成开销完全取决于电路的大小，更具体地说，是使用以上六个电路中的哪一个。

换句话说，周期是唯一重要的内容。

需要注意的是，最近有关于能够利用稀疏性的证明系统的讨论，例如来自 a16zcrypto 的 Lasso + Jolt，该系统依赖于在同态承诺上提交结构化的多线性扩展——以及来自 Ulvetanna 的 Binius，这是一个具有硬件友好编码的二进制证明系统。这两者都与 RISC Zero 相关。我个人认为 Lasso + Jolt 和 Binius 是不同的“丰收树”，它们包含非常不同的、互补的技术，未来的 RISC Zero 版本或其社区变体可以进行选择。

既然周期是我们需要考虑的唯一因素，我们现在将注意力转向那些可以帮助我们研究特定程序周期的工具。

深入了解周期的分析器

作为我们研究工作的一部分，我们为 RISC Zero 构建了一个分析工具，称为 profiler0。

https://github.com/l2iterative/profiler0

请记住——要优化代码，第一步是识别主要瓶颈。分析器 tool profiler0 使我们能够在代码中添加一些计时器，如“start_timer!”，“stop_start_timer!” 和 “stop_timer!” 的调用，用于验证 RISC Zero 中的 FHE，如下所示。

start_timer!("Total");

start_timer!("Load the bootstrapping key");

let bsk = black_box(unsafe {
    std::mem::transmute::<&u8, &[GgswCiphertext; 16]>(&BSK_BYTES[0])
});

stop_start_timer!("Load the ciphertext to be bootstrapped");

let c = black_box(unsafe {
    std::mem::transmute::<&u8, &LweCiphertext>(&C_BYTES[0])
});

stop_start_timer!("Perform trivial encryption and rotation");

let lut = black_box(GlweCiphertext::trivial_encrypt_lut_poly());
let mut c_prime = lut.clone();
c_prime.rotate_trivial((2 * N as u64) - c.body);

stop_start_timer!("Perform one step of the bootstrapping");

// set to one step
for i in 0..1 {
    start_timer!("Rotate");
    let rotated = c_prime.rotate(c.mask[i]);

    stop_start_timer!("Cmux");
    c_prime = cmux(&bsk[i], &c_prime, &rotated);

    stop_timer!();
}

stop_timer!();
stop_timer!();

这让我们可以看到代码的不同部分对周期数量的贡献。分析器跟踪来宾程序的执行并对周期进行统计。结果可以在 这里 找到。

分析器的结果可以总结如下。

• 加载引导密钥： 15 条指令，3297 周期

• 加载待引导的密文： 11 条指令，11 周期

• 进行简单加密和旋转： 66,096 条指令，123,982 周期

• 进行 1024 步中的一步引导： 151,619,979 条指令，159,597,740 周期

  • 旋转： 55,930 条指令，75,670 周期

  • Cmux： 151,564,031 条指令，159,520,958 周期

总计为 151,686,471 条指令和 159,726,565 个周期。

我们可以立即得出一些关于成本来源的结论——cmux，因为它占据了 99% 的指令和 99% 的周期。注意这只是整个引导过程中的单一步骤。完整的 TFHE 引导示例有 1024 个这样的步骤。

分析的自然下一步是进入 cmux 函数进行详细拆解。我们在使用的 TFHE 库中添加以下分析代码。

pub fn cmux(ctb: &GgswCiphertext, ct1: &GlweCiphertext, ct2: &GlweCiphertext) -> GlweCiphertext {
    start_timer!("subtract the ciphertext");
    let mut res = ct2.sub(ct1);
    stop_start_timer!("external product");
    res = ctb.external_product(&res);
    stop_start_timer!("add the result");
    res = res.add(ct1);
    stop_timer!();
    res
}

我们还将分析代码放入 external_product 函数，因为它对于性能至关重要。值得注意的是，分析器接受静态消息以及运行时动态生成的消息。

impl GgswCiphertext {
    /// Performs a product (GGSW x GLWE) -> GLWE.
    pub fn external_product(&self, ct: &GlweCiphertext) -> GlweCiphertext {
        start_timer!("apply g inverse");
        let g_inverse_ct = apply_g_inverse(ct);
        stop_start_timer!("multiply");

        let mut res = GlweCiphertext::default();
        for i in 0..(k + 1) * ELL {
            start_timer!(format!("i = {}", i));
            for j in 0..k {
                res.mask[j].add_assign(&g_inverse_ct[i].mul(&self.z_m_gt[i].mask[j]));
            }
            res.body
                .add_assign(&g_inverse_ct[i].mul(&self.z_m_gt[i].body));
            stop_timer!();
        }
        stop_timer!();
        res
    }
}

这让我们可以对 cmux 的指令进行更详细的拆解，如下所示。需要注意的是，分析器会注入一些指令，因此 cmux 的周期计数略有增加。

• 减去密文： 38,495 条指令，46,163 周期

• 应用 G 逆： 79,991 条指令，167,498 周期

• 与 i = 0 相乘： 37,840,587 条指令，39,875,485 周期

• 与 i = 1 相乘： 37,840,584 条指令，39,759,520 周期

• 与 i = 2 相乘： 37,840,584 条指令，39,802,186 周期

• 加上结果： 50,816 条指令，70,525 周期

总计为 151,565,973 条指令和 159,619,414 周期。

分析器还向我们提供了触发大量周期的指令位置。可以在分析器的新输出中找到相同的这里。有趣的是，几个位置出现得非常频繁，表明它们可能在循环中。

0x200d18, 0x200d20, 0x200d74, 0x200d78, 0x200d7c

这些地址彼此接近，表明它们可能来自于单个函数的汇编代码，并且该函数被调用的频率较高，从而贡献了大部分周期。尽管分析器确实显示出该指令，例如 0x200d74 出现的频率极高，但理解一条指令的功能需要上下文。

是什么最好的获取上下文的方法？答案明确——“回到现场”。

使用 GDB 进行动态代码分析

我们需要一个工具，将我们带回现场，查看代码发生了什么。作为我们研究工作的一部分，我们为 RISC Zero 来宾程序构建了一个 GDB 存根。GDB 存根就像可以使 GDB 与 RISC Zero 一起工作的“粘合代码”。

我们称这个 GDB 存根为“gdb0”。

https://github.com/l2iterative/gdb0

要开始，我们首先编译带有调试信息的程序。以下步骤实现这个目标。

首先，在“guest”目录的 Cargo.toml 中，添加以下内容，以便即使在调试模式下编译程序，也能应用必要的优化（否则，Rust 程序会慢得离谱）。

[profile.dev]
opt-level = 3

[profile.dev.build-override]
opt-level = 3

然后，我们用一个环境变量编译来宾程序，这样会开启 RISC Zero 调试模式。

RISC0_BUILD_DEBUG=1 cargo run

接着，我们将编译好的来宾程序（标准的 RISC-V 代码 ELF 文件）复制粘贴到 gdb0 目录。此操作使用的 Bash 命令在你本地环境中可能有所不同，不过在我们的设置中，我们只需在 gdb0 目录中执行以下操作。请确保将编译的程序复制到“debug”目录，而不是“release”目录。

cp ../vfhe0/target/riscv-guest/riscv32im-risc0-zkvm-elf/debug/method code

我们应重新运行分析器，因为该函数的位置可能有所不同。分析器的新结果附在 这里。我们可以看到地址 0x200db0、0x200db4、0x200db8、0x200dbc 是经常导致巨大周期（由于读/写）的指令。

我们现在开始 GDB。有关如何运行 GDB 的详细信息，请参考上面的 GitHub 仓库。基于上面的分析器输出，我们在 0x200db0 设定一个软件断点。接着，我们请求 GDB 继续执行，最终结束在以下屏幕上。

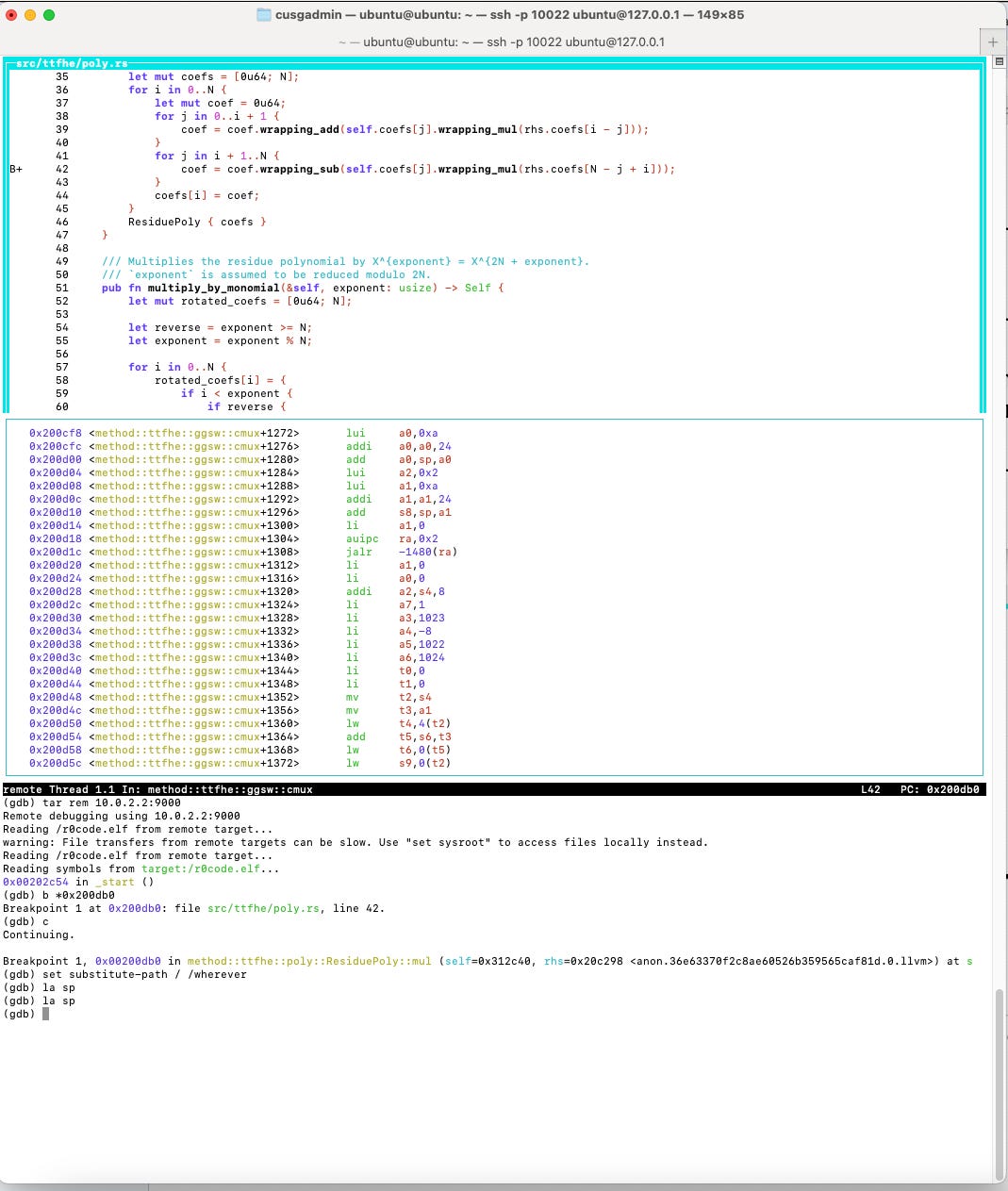
图 5：到达导致大量开销的循环。

这让我们可视化 0x200db0 被频繁调用的原因及其所属位置。这是多项式乘法函数的内部循环。请注意，当我们设置断点时，GDB 已经告诉我们该代码对应于“src/ttfhe/poly.rs” 文件的第 42 行。

我们可以看到 Rust 源代码是如何转换为 RISC-V 指令的。例如，这个内部循环执行 64 位整数乘法，通常看到这个结构时“bne”指的是循环的结束。

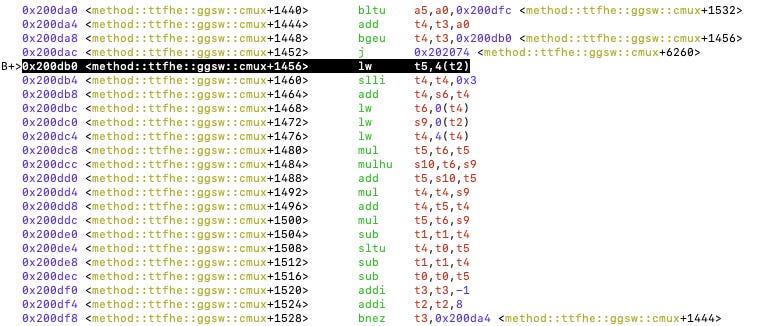
图 6：内部循环执行 64 位整数乘法和累加。

RISC Zero 使用的是 32 位的 RISC-V，我们可以看到 64 位整数乘法是通过 32 位整数操作来模拟的，例如 mul、mulhu 和 add。Rust 在编译时执行了这样的操作，你可以试验这种情况，并在 Godbolt 上检查一致性。

如今，我们通过有关程序执行的所有信息可以拿出战斗计划。

诊断我们的代码

随着我们文章的结束，我们想讨论我们该如何优化性能。这也将是后续文章的主题。

首先，正如 VFHE 库所声明的，当前执行负循环Rollup的算法是一个非常简单的算法，时间复杂度为 O(n^2)。换句话说，当我们在大小为 1024 的两个向量上执行此操作时，代码必须执行 1048576 次64 位整数的乘法，以及中间的数据加载/保存开销。

我们知道还有其他的算法。首先，由于模数是 2^64，且为了与 Zama 兼容，我们排除了 NTT，因此没有太大希望进行整数 NTT。然而，我们可以像 Zama 所用那样，使用复数上的浮点 NTT。Zama 使用浮点数这一看似复杂的方法的原因很简单：在现代 CPU 上，浮点数并不昂贵，因为它只需几个周期，如整数乘法，比整数除法便宜得多。

然而，这在 RISC-V 或 RISC Zero 中并非如此。官方文档提到“浮点操作如加法、减法、乘法和除法的基本操作可能需要 60-140 周期。”在 RISC Zero 中，浮点操作则要昂贵得多。根据我们与 Zama 的 Rand Hindi 的交谈，我们得出结论，带浮点的复数 NTT 可能不是 ZK 的解决方案。

剩下的选项是非 NTT 高效多项式乘法（或更具体，负Rollup）。我们计划使用 Karatsuba 算法，该算法通过分治的方式来执行计算，从而产生亚二次的开销。

这应该能够带来两个数量级的加速。

另一个优化的机会是寻找特定应用的优化机会。在 TFHE 中，当我们进行引导时，我们将 GGSW 密文与 GLWE 密文相乘，而这种乘法的一个非常有趣的地方是 GLWE 将被分解成所有数出奇小的格式（即，应用逆 G 变换）。

这意味着我们实际上不需要进行 64 位整数的计算。根据我们的配置，逆 G 变换的输出仅仅是 8 位。 Karatsuba 算法 可能在此过程中添加数字，只要 Karatsuba 的深度不太大，16 位表示应是可行的，以容纳中间的结果。在 32 位数中，我们可以编码两个这样的数字，这将节省内存空间及加载/保存的开销，并且我们可以按需解码。

最后，让我们回到内部循环及其汇编代码。

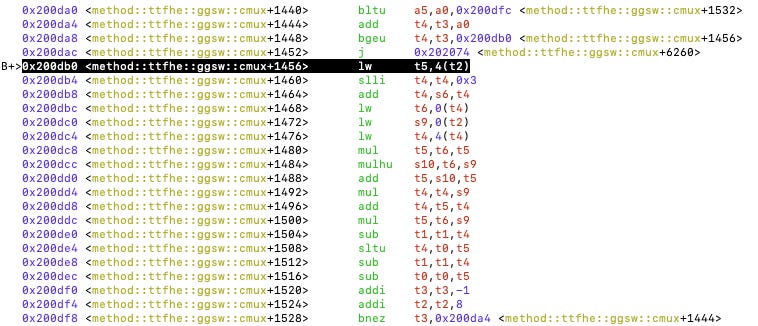
图 6：内部循环执行 64 位整数乘法和累加。

内部循环每次迭代大约包含 20 条指令。我们可以想象，如果我们使用上述的压缩表示，可以节省一些指令。然后，让我们观察其余的指令。有几条快速的观察。

• 0x200da4 - 0x200dac 是一个健全性检查，用于检测代码是否正在访问切片边界外的位置。这是 Rust 出于安全考虑的方法。但是，我们可能希望删除它。

• 0x200db4 - 0x200dc4，t4 用于存储 rhs.coefs[N - j + i] 的地址。看起来非常可能简化这个计算，例如，不应该使用“slli”操作将值左移 3 位以乘以 8。我们可以使用两个指针，在迭代过程中移动，一个加 8，一个减 8。这可以在 0x200df0 - 0x200df4 的代码片段中实现。

• 如果我们使用上述的压缩表示，则有助于在一项迭代中完成两步操作。

平均而言，每次乘法似乎贡献 36 个周期 (=37840587 / 1024 / 1024)。我们应该能够通过这样的优化减少这个数字，由于 Karatsuba 可以降低乘法次数，我们可以减少整体乘法开销。

有一个有趣的想法是看看我们是否可以使用 RISC Zero 的 bigint 系统调用来模拟三个 16 位乘以 64 位的计算，但尚不确定这样做是否更有效，因为附带的打包和解包开销也很高。

最后，如果我们想在合理的时间内构建整个证明（经过 1024 步），我们需要一些加速：硬件加速和软件加速。我们将尝试 RISC Zero 的 Metal GPU 优化，这似乎非常强大，并且我们将研究 RISC Zero 的递归性，以及如何并行生成整个计算的证明，从而能够线性扩展以降低延迟。

我们还特别关注 RISC Zero 的 Zirgen 工具，这可能开启定制证明系统的可能性，特别添加向量化指令以帮助执行负Rollup。另一个要关注的内容是 Jeremy Bruestle 在 RISC Zero Discord 中讨论的概率检查协议，它给出了 O(n) 的复杂性，但具体细节仍需完善。

长话短说，期待在下一篇 RISC Zero 系列文章中验证 FHE。

在 l2iterative.com 找到 L2IV，并在 Twitter 上关注 l2iterative

作者： Weikeng Chen，L2IV 研究合伙人（ @weikengchen）

• 原文链接： l2ivresearch.substack.co...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～