Schnorr 簽名：透過 ecrecover 實現高效驗證

在數位安全和區塊鏈技術的背景下，數位簽章扮演著至關重要的角色。本文將深入探討 橢圓曲線密碼學（ECC） 和 Schnorr 簽名 的運作原理，以及其如何通過聚合和批量驗證來提升效率。特別是，我們將與其他數位簽章算法（如 ECDSA）進行對比，分析其優劣。最後，還將探討 Schnorr 簽名與 ecrecover 在區塊鏈上的應用。

橢圓曲線密碼學（ECC）：私鑰與公鑰的基礎

在 ECC 中，我們使用橢圓曲線上的點運算來生成公私鑰對。ECC 的安全性依賴於 橢圓曲線離散對數問題（ECDLP），這是一個數學難題，難以通過公鑰推導出私鑰。私鑰 k_priv 是簽名者的隨機數，公鑰則是私鑰與橢圓曲線上的基點 G 的點乘結果： K = k_priv ⋅ G

橢圓曲線上的加法與倍加運算

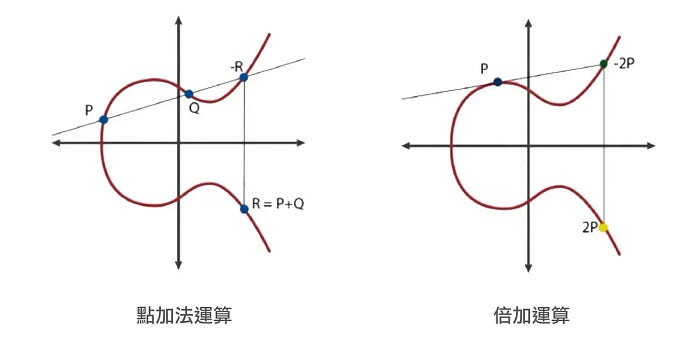
點加法運算

在橢圓曲線上，點加法 是將兩個點 𝑃 和 𝑄 相加，並得到新點 𝑅 的過程。這是橢圓曲線上最基本的運算之一：

• 相連：將點 𝑃 和 𝑄 相連，這條直線會與橢圓曲線相交於第三個點。
• 反射：將這個相交點相對橢圓曲線進行鏡像反射，得到點 𝑅 = 𝑃 + 𝑄。

倍加運算

當兩個點相同時，即 𝑃 = 𝑄，我們進行的是倍加運算，其過程如下：

• 找切線：在點 𝑃 的位置計算曲線的切線。
• 交點反射：找到切線與曲線的相交點，並將相交點鏡像反射，得到新的點 𝑅 = 2𝑃。

點乘法的高效計算

點乘法是 ECC 中的一個關鍵操作，計算公式為 K = k ⋅ G，這裡的 k 是私鑰，G 是橢圓曲線上的基點。為了提高運算效率，常使用 加倍-加法算法（Double-and-Add Algorithm），這種方法可以通過二進制優化點乘法的計算。

加倍-加法算法（Double-and-Add Algorithm）!!

為了高效地計算點乘法，我們可以使用二進制方法進行優化，稱為加倍-加法算法。在對 k 進行點乘（ ⋅ G）時，透過將 k 轉換為二進制數，我們可以將其其分解為加倍和加法的組合運算。

例如，對於 k = 13，其二進制表示為 1101，我們可以通過以下方式計算：

13 ⋅ G = 2³ ⋅ G + 2²⋅ G + 2⁰ ⋅ G

通過倍加運算計算 2³ ⋅ G 和 2² ⋅ G，並將它們相加來得到最終結果。

如此，我們可以更快速地得到點乘結果。

橢圓曲線離散對數問題（ECDLP）

橢圓曲線離散對數問題（Elliptic Curve Discrete Logarithm Problem, ECDLP） 是橢圓曲線密碼學（ECC）的核心問題，整個 ECC 的安全性基礎正是依賴於該問題的計算困難性。ECDLP 是一個難以逆推的數學問題，K = k_priv ⋅ G ，給定橢圓曲線上的兩個點 K（公鑰）, G（曲線基點），我們很難找到將它們聯繫起來的標量倍數 k_priv（私鑰），這就是 ECDLP 的具體表現。

數位簽章與 Schnorr 簽名

數位簽章的概述

數位簽章 是一種加密技術，用來保證訊息的完整性和驗證簽署者的身份。可以將其類比為現實生活中的合約蓋章流程，過程如下：

• 合約 對應於待簽名的訊息（即消息 𝑚）。
• 印章 對應於由私鑰生成的數位簽名，私鑰是唯一的且需要保密，就像每個人獨特的印章。
• 驗證過程 類似於核對印章。接收者（或第三方）可以通過公開的簽名資訊（如公鑰），來驗證簽署者的身份，並確保消息未被篡改。

數位簽章在數據保護、身份驗證、電子交易和區塊鏈技術中扮演著至關重要的角色。

Schnorr 簽名

Schnorr 簽名 是一種基於橢圓曲線的數位簽章算法。它相較於常用的 ECDSA 簽名更簡單且高效，尤其適合多重簽名場景。在區塊鏈和其他需要多個簽名的應用中，Schnorr 簽名因為支持簽名聚合，能夠顯著減少運算成本並提高效能。

Schnorr 簽名的生成過程

1. 隨機數生成：簽名者選擇一個隨機數 r，並計算點 R = r ⋅ G。
2. 生成簽名：計算雜湊值 H(m || K || R)，並使用私鑰計算簽名值，其中 H()為雜湊函數，m 為簽名訊息：

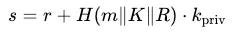
Schnorr 簽名的驗證過程

驗證者收到簽名後，可以使用簽名者的公鑰來檢查簽名的有效性。具體的驗證過程如下：

1. 驗證公式：

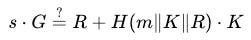
2. 計算等式兩側並檢查等式是否成立：

• 計算 𝑠 ⋅ 𝐺。
• 計算 𝑅 + H(m || K || R) ⋅ 𝐾，其中 𝐾 = 𝑘_priv ⋅ 𝐺 是簽名者的公鑰。

如果等式成立，則簽名驗證成功，表明訊息來自正確的簽名者，並且消息未被篡改；如果等式不成立，則表示簽名無效。

Schnorr 簽名的聚合與批量驗證

Schnorr 簽名有兩個顯著的優勢： 簽名聚合 和 批量驗證。

簽名聚合

假設有 n 位簽名者，每個簽名者的簽名公式為：

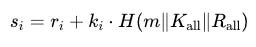
其中：

• K_all = K_1 + K_2 + … + K_n 是所有簽名者的公鑰加總。
• R_all = R_1 + R_2 + … + R_n 是所有簽名者的隨機點加總。

聚合簽名的總簽名值為： s_all = s_1 + s_2 + … + s_n

最終的驗證公式為：

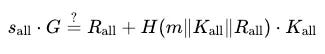
聚合簽名技術允許多個交易者將各自的簽名在鏈下進行聚合，最終只需提交一組簽名即可完成所有簽名驗證，即一次交易就可完成一次的聚合簽名，從而顯著提升交易效率並減少鏈上數據量。

Key Cancellation Attack 的風險

然而，簽名聚合的過程也伴隨著風險，尤其是 Key Cancellation Attack（公鑰抵消攻擊）。在這類攻擊中，惡意簽名者可能通過選擇特定的公鑰或隨機點來與其他簽名者的公鑰抵消，導致被抵消的簽名者等同於實質上被除名。例如，某位簽名者(1)在得知簽名者 (2) 所選擇的 R_2 與 K_2 後，故意選擇其公鑰為

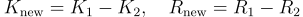
當進行簽名聚合時，最終的聚合公鑰 K_all, R_all​ 會變成：

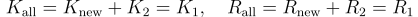
這時，實際上 K_2​ 完全被抵消，簽名聚合結果將只剩下 K1​ 作為唯一有效的公鑰，導致 K_1 的擁有者（攻擊者）可以完全控制最終的簽名，因為最終的簽名驗證將只依賴於 K_1, R_1​：

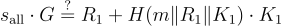
這樣，攻擊者可以完全操控最終的簽名驗證過程，甚至可能竄改交易或簽名內容而不被發現。

MuSig: 挑戰因子與承諾機制

ref : https://github.com/chainx-org/chainx-technical-archive/blob/main/LuoJianMan/Taproot/02_Understand-Schnorr-and-Musig.md#key-cancellation-attack

MuSig 協議為了防止公鑰抵消攻擊（Key Cancellation Attack），使用了 挑戰因子（Challenge Factor） 和 承諾機制（Commitment Mechanism） 來增強安全性。這些機制確保每個簽名者無法通過選擇特定的公鑰或隨機數來影響最終的簽名結果。

挑戰因子（Challenge Factor）

挑戰因子是針對每個簽名者計算的一個動態調整參數，它的目的是讓每個簽名者的公鑰在聚合簽名過程中無法被其他參與者抵消或操控。挑戰因子是根據所有簽名者的公鑰生成的，具體如下：

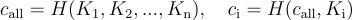
這個挑戰因子會被應用到每個簽名者的公鑰上，生成一個調整後的公鑰：

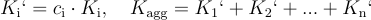
這樣一來，即便攻擊者試圖操控公鑰來抵消其他簽名者的公鑰，也難以實現。挑戰因子的引入使得惡意簽名幾乎無法精確計算出能剛好抵消他人公鑰的值，從而有效防止攻擊。因為挑戰因子將雜湊納入最終公鑰的計算，隨意更改 K_i​ 都會導致計算出完全不同的 K_i’。

承諾機制（Commitment Mechanism）

承諾機制確保每個簽名者無法在收到其他簽名者的隨機數後，修改自己的隨機數。具體過程如下：

• 首先，每個簽名者生成一個隨機數 r_i 和相應的公開隨機數 R_i=r_i ⋅ G，並將 R_i​ 的雜湊值 C_i = H(R_i) 作為承諾傳送給其他簽名者。
• 當所有簽名者交換了這些雜湊承諾 C_i​ 後，參與者再交換實際的隨機數 R_i。
• 每個簽名者在接收到其他人的隨機數後，會檢查這些隨機數是否與先前的承諾 C_i​ 相符。如果不符，則該簽名者可能在作弊，整個簽名過程會中止。
• 如果相符，則可以確定簽名者在得知他人隨機數後，未曾修改自己的隨機數。並進行隨機數聚合：

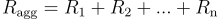
承諾機制確保參與者無法根據其他人的隨機數更改自己的隨機數，這大大增加了簽名過程的安全性。

透過 挑戰因子 和 承諾機制 的雙重防禦，MuSig 使得參與者無法進行公鑰抵消攻擊或操控隨機數，確保多重簽名的安全與穩定。因此，我們可以安全地進行以下聚合：

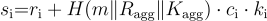
聚合 s_1, s_2, …, s_n，並兩側同乘以 G ，即可得到下式

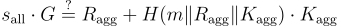
批量驗證

批量驗證 是提升驗證效率的一種方法，允許對多個簽名進行並行驗證，從而減少整體的點乘次數。為了確保安全性，批量驗證引入了隨機權重 a_i，以防止攻擊者利用特定的線性組合，試圖讓無效簽名通過驗證。

ex.攻擊者可以嘗試生成兩個無效的簽名 s_1​ 和 s_2​，並使這兩個無效簽名的點乘結果在驗證過程中互相抵消。這樣，在批量驗證中，驗證算法會錯誤地認為這些簽名是有效的。

優化的批量驗證公式：

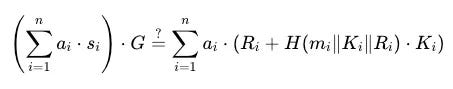
• 左側是所有簽名的隨機加權總和後進行一次點乘。
• 右側對每個簽名進行加權點加運算，涉及隨機點 R_i 和公鑰 K_i，並基於每條消息 m_i 計算雜湊值。

點乘次數分析

• 左側：一次點乘（加權總和後的點乘）。

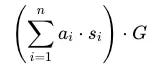
• 右側：簽名仍需要 n 次點乘（每個 H(m_i || K_i || R_i) ⋅ K_i 一次點乘）。

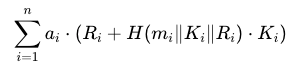
總點乘次數為 n + 1 次，相比單獨驗證每個簽名需要 2n 次點乘，批量驗證將運算成本減少了接近一半，從而顯著提高了驗證效率。

ECDSA 簽名與 ecrecover 在以太坊中的應用

ECDSA 簽名 是橢圓曲線數位簽章算法的一個變種，廣泛應用於區塊鏈中。以太坊提供了 ecrecover 函數來恢復簽名者的公鑰，從而驗證消息的真實性。

ECDSA 簽名的生成過程

1. 隨機數生成：

簽名者選擇一個隨機數 𝑘，並計算橢圓曲線點 𝑅 = 𝑘 ⋅ 𝐺，其中 𝐺 是橢圓曲線上的生成點。

取點 𝑅 的 x 坐標作為簽名中的參數 𝑟，即： 𝑟 = 𝑅𝑥 ，其中 𝑅𝑥 是點 𝑅 的 x 坐標。

2. 生成簽名：

計算訊息的雜湊值 𝑒 = 𝐻(𝑚)，其中 𝑚 是待簽名的訊息。

根據私鑰 𝑘_priv，計算簽名值 𝑠 = k^-1 ⋅ ( 𝑒 + 𝑟 ⋅ 𝑘_priv) mod 𝑛 其中，𝑛 是橢圓曲線的階。

3. 輸出簽名：

最終的簽名由兩個參數 (𝑟,𝑠,𝑣) 組成，簽名者將其發送給驗證者。

ecrecover 的原理

在 ECDSA 簽名過程中，我們生成了三個主要參數：

• 𝑟：橢圓曲線中的點 𝑅 的 x 坐標。
• 𝑠：計算出的簽名值，基於私鑰、消息的雜湊值和隨機數 𝑘。
• 𝑣：確定簽名的奇偶性，用於在橢圓曲線中選擇正確的點。

pragma solidity ^0.4.0;
contract test {
    function verify(bytes32 _message, uint8 _v, bytes32 _r, bytes32 _s) constant returns (address) {
       bytes memory prefix = “\x19Ethereum Signed Message:\n32”;
       bytes32 prefixedHash = sha3(prefix, _message);
       address signer = ecrecover(prefixedHash, _v, _r, _s);
       return signer;
   }
}

以太坊的 ecrecover 函數從消息雜湊、簽名 𝑟, 𝑠, 𝑣 中恢復出簽名者的公鑰地址，即 PublicKey = ecrecover(e, v, r, s)。具體步驟如下：

1. 取得消息的雜湊值 𝑒 = 𝐻(𝑚)。
2. 使用簽名的 𝑟, 𝑠, 𝑣 恢復出簽名者的公鑰。
3. 驗證該公鑰是否與消息的簽署者匹配。

為了推導出公鑰，我們可以將公式兩邊同時乘以橢圓曲線上的生成點 𝐺：

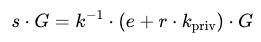
這可以展開為：

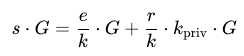
其中，K = k_priv ⋅ G 是公鑰，我們移到等式左邊，兩邊同乘以 k ⋅ r^-1：

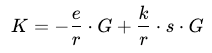
化簡後，並利用 𝑅 = 𝑘 ⋅ 𝐺，我們可以得到最終公式：

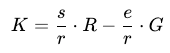
這樣，我們就能成功地從簽名和消息雜湊中推導出公鑰 𝐾。

為什麼使用 ecrecover 而不用 ecMul 來驗證？

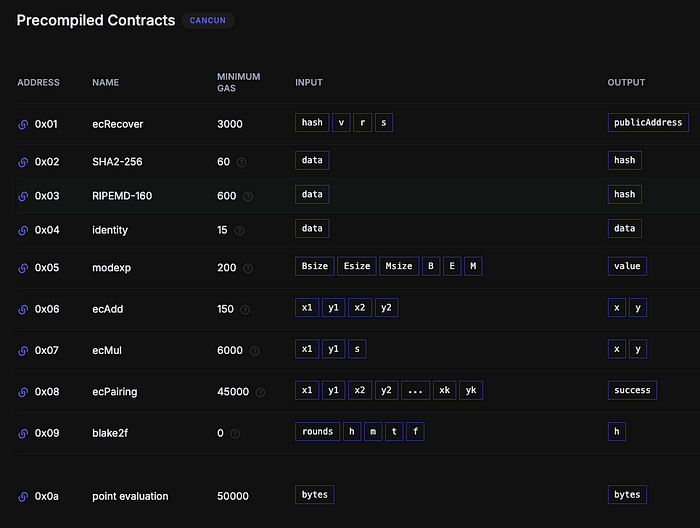
From : https://www.evm.codes/precompiled

上圖顯示了各個以太坊虛擬機（EVM）預編譯函數及其所需的最低 Gas。可以看到， ecMul 函數需要 6000 Gas，而 ecrecover 只需要 3000 Gas。由於 ecrecover 相較於 ecMul 消耗的 Gas 較少，因此在特定場景中選擇使用 ecrecover 能更有效節省運行成本。

Schnorr 簽名與 ecrecover 的結合應用

來源 : Schnorr signature verification ecrecover hack

在以太坊中， ecrecover 作為一個預編譯合約（precompile），主要用於驗證基於 Secp256k1 橢圓曲線的 ECDSA 簽名。通過對輸入參數進行一些調整，我們可以擴展其功能來支持 Schnorr 簽名的驗證，從而進一步妥善利用 ecrecover 達到低成本的驗證消耗。

我們將原先的 ecrecover(e, v, r, s) 以下面的參數分別帶入

• e’ = -s ⋅ K_x
• v’：表示點 P 的奇偶性。
• r’ = K_x
• s’ = -e ⋅ K_x

我們可以利用前述用 ecrecover 還原公鑰 K 點的公式，將其中的參數替換為 Schnorr 簽名情境中的參數，從而實現 Schnorr 簽名的驗證功能：

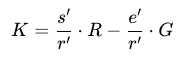
其中 r’ = K_x，K 將取代 ecrecover 中的 R，並代入 e’, s’, r’，我們可以得到：

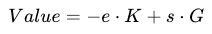
這與 Schnorr 簽名的驗證公式對應，移項一下，我們可以看到等式右邊與之前推導出來的公式一致：

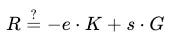
因此，我們只需要將 ecrecover 的結果與 R 進行對比即可完成 Schnorr 簽名的驗證。

Schnorr 簽名與 ECDSA 的對比

優勢對比

1. Schnorr 簽名的簡潔性：數學結構更簡單，計算成本更低。
2. 多重簽名與聚合簽名：Schnorr 支持簽名聚合，大大提高了多重簽名應用中的效能。
3. 批量驗證：可以一次性驗證多個簽名，顯著減少計算資源。

隨機數重用的風險

隨機數的唯一性是數位簽名算法安全性的關鍵。如果兩次簽名重用了相同的隨機數 k，攻擊者可能通過數學運算推導出簽名者的私鑰，從而破壞簽名系統的安全性。這一風險並非僅限於理論，實際中已經發生多起因為隨機數重用導致密鑰洩漏的事件。因此，在數位簽名的應用中，務必要確保每次簽名都使用唯一的隨機數。

結論

綜合以上討論，Schnorr 簽名在區塊鏈應用中展現出顯著的優勢，尤其是在多重簽名場景和批量驗證方面。與 ECDSA 簽名相比，Schnorr 簽名因其數學結構更為簡單，計算成本更低，特別是在支持簽名聚合的情況下，大大提升了性能。此外，Schnorr 簽名還有效避免了 ECDSA 中隨機數重用所帶來的安全風險，進一步提升了安全性和可靠性。

在實際應用中，通過對現有的以太坊 ecrecover 函數進行調整，Schnorr 簽名的驗證可以被有效整合到區塊鏈中，從而充分利用其高效和安全的特性。隨著區塊鏈技術的發展，Schnorr 簽名有望在未來成為更廣泛應用的數位簽章標準，為去中心化應用提供更高效、安全的簽章解決方案。

附註

為什麼比特幣最初選擇ECDSA而非Schnorr簽名？

Schnorr簽名算法是由著名的密碼學家Claus P. Schnorr創造的，但該算法在2008年之前受專利保護，這專利直到Satoshi Nakamoto發布比特幣白皮書的前幾個月才到期。雖然專利到期了，但當時Schnorr簽名還未經過充分的測試和應用，也缺乏足夠的流行度來保障比特幣這樣一個重要網絡的安全性。

Satoshi 最終選擇了 ECDSA（橢圓曲線數位簽名演算法） 作為比特幣的簽名算法，這是因為在當時，ECDSA 已經是非常成熟且廣泛應用的算法。它已經被密碼學界充分驗證，並應用於許多安全協議中。相比之下，Schnorr 雖然技術上具有一些優勢，但當時並不普及，缺乏實際應用的驗證。

因此，為了確保比特幣網絡的安全性和穩定性，Satoshi 選擇了成熟的 ECDSA 來保障比特幣系統的可靠性和安全性。

特別感謝：

這篇文章的撰寫契機，來源於在 Zeus Network 研究 Schnorr 簽名過程中的啟發。在此特別感謝公司前輩 Jim 和 Dean 的指導，無論是寫作技巧還是技術闡述和理解，他們的寶貴建議都為本文提供了莫大的幫助。

此外，如果有人對於在 Solana 區塊鏈上高效驗證 Schnorr 簽名有興趣，強烈推薦參考由技術大神 Dean 撰寫的專案： solana-nostd-secp256k1-recover。該專案提供了關於 Schnorr 簽名驗證的詳細實現，以及如何善用 solana syscall 高效驗簽的能力，具有很高的應用價值！

補充資料：

1. The past, present, and future of threshold Schnorr signatures with Chelsea Komlo

2. What Are Schnorr Signatures in Bitcoin?

• 本文转载自： medium.com/taipei-ethere...