KZG与常见的SNARK零知识算法特点分析

一. KZG算法

1.算法特点

• 类型：多项式承诺方案 (Kate-Zaverucha-Goldberg)，基于椭圆曲线双线性配对。
• 主要优势：承诺体积小，一次性承诺可验证多点值；单点验证效率高。

2.算法复杂度

• 证明生成：对多项式 \sum f_i x^i 而言，生成承诺的过程相对高效，主要是对公共参数 {g^{\tau^i}} 做若干次幂运算与乘法
• Trusted Setup：需要一次“Powers of Tau”仪式，若秘钥 \tau 泄露可破坏系统安全
• 量子时代：对强大的量子计算不具备抗性，需要后续做替换或升级

3. 应用场景

• 数据可用性：EIP-4844（Proto-Danksharding）中对大块数据（Blob）做KZG承诺
• Plonk等SNARK：常用KZG作为多项式承诺后端
• 链上验证：在单点或少数点值验证中非常高效

二. Groth16 算法

1 算法特点

• 类型：零知识SNARK 协议，基于 Pairing + R1CS（Rank-1 Constraint System）。
• 最大亮点：证明体积极小（几十到几百字节），验证时间短。

2.算法复杂度

• 生成证明：为一个大小为 n 的电路生成证明时，复杂度一般 O(n) 量级的多次配对与多项式运算；
• 验证：验证通常只需 2~3 次配对运算，极其迅速。

3.安全性

• 需单电路Trusted Setup：对每个电路都要执行一次可信生成，若仪式被攻破，则可伪造证明；
• 安全假设：椭圆曲线DLOG与配对问题；量子计算下易受冲击。

4.应用场景

• 隐私代币：Zcash、Tornado Cash；
• zk-Rollup（早期方案）利用其极短证明；
• 对安全/成熟度要求高但能容忍单电路或固定电路的场景

三. Sonic算法

1.算法特点

• 目标：解决Groth16“单电路”可信设置限制，提出可更新、通用的SRS；
• 理念：在证明与验证性能上与Groth16相近，但大幅提升对电路/应用的灵活度。

2.算法复杂度

• 生成证明：与Groth16同级别，通常 O(n)；

• 验证：也需要若干配对运算，复杂度与电路深度关联度小。

3.安全性

• 可更新/通用的SRS：多次多方仪式可增强安全性；
• Pairing安全：若基础曲线失守，则系统易受影响。

4.应用场景

• 多电路共享SRS：Layer2 或 DApp 频繁升级、多个不同电路的情况；

• 通用零知识平台：提升使用便捷度，减轻仪式负担。

四. Fractal算法

1.算法特点

• 定位：强调递归SNARK能力和通用电路支持；
• 特色：在固定的通用SRS下对不同规模电路均可做高效证明，并可进行嵌套/递归。

2.算法复杂度

• 证明生成：典型地为 O(n \log n) 或 O(n) 量级，具体取决于电路结构；
• 验证：仍是几次配对计算，或更复杂的多项式检查，但规模与电路本身无关。

3.安全性

• 可信设置：可以采用可更新或通用SRS；
• 基础安全：同样使用 Pairing + DLOG 假设；需防量子攻击。

4.应用场景

• 递归场景：如连续区块状态更新或多轮证明累加；
• 区块链合约：需要高度可扩展电路与复用SRS的应用。

五. Halo2算法

1.算法特点

• 提出：Zcash团队推出，用于提升零知识证明在复杂电路与递归场景的友好度；
• 显著改进：实现无信任或轻信任设置、可支持递归Proof、编程接口更灵活。

2.算法复杂度

• 生成证明：在Halo2中，生成环节通常是 O(n) 或 O(n \log n)，随具体电路而变；
• 验证：执行多项式承诺与有限次椭圆曲线运算，复杂度较小。

3.安全性

• 可选Trusted Setup：可使用通用SRS或无SRS模式，具体看实现；
• 基于离散对数：后量子不安全，若椭圆曲线被量子算法攻破则失效。

4.应用场景

• Zcash 升级：在 Orchard 协议中使用 Halo2；
• 递归零知识：多层Proof嵌套、层层验证安全；
• 可扩展电路：适合多方、动态电路场景

六.SuperSonic

1.算法特点

• 目标：兼顾“无可信设置”与“证明简洁”两大诉求；
• 思路：使用内积证明 (IPP) 等技术替代 Pairing 强依赖，减少多方仪式需求。

2.算法复杂度

• 生成证明：同级别零知识电路通常是O(n)，但因无TS可能在某些优化上稍逊于 Groth16；
• 验证：内积证明加多项式检验，时间比 Groth16 略多，但仍相对高效。

3.安全性

• 无可信设置：部署更易，但也意味着部分性能折衷；
• 依赖椭圆曲线或群离散对数：需评估量子风险。

4.应用场景

• 对“透明性”需求高：不愿意或无法组织多方仪式的项目；
• 通用SNARK：隐私交易、Layer2 等都可潜在使用，但目前并未像 Groth16/Plonk 那样流行。

七. Marlin

1.算法特点

• 定位：类似Sonic/Plonk，提供可更新/通用SRS，适合大规模电路；
• 创新：简化约束表达与验证流程，在保持证明简短的同时保证高速验证。

2.算法复杂度

• 生成证明：O(n) 级电路转换 + 多项式运算；
• 验证：少数配对或内积运算，大小与电路规模无关。

3.安全性

• 同Pairing SNARK：若曲线安全破裂或量子算法出现，则系统脆弱；
• 通用/可更新SRS：通过多方参与提高抵御私钥泄露的能力。

4.应用场景

• 多DApp合并：共享公共参数，方便多个智能合约、Rollup 同时部署；
• 较灵活电路：Marlin更易支持多样化的约束结构。

八. Plonk算法

1. 算法特点

• 热度：现今最受关注的通用SNARK协议之一；
• 优势：

🍊 通用且可更新SRS；

🍊 验证速度、证明体积与Groth16相差不大；

🍊 支持更灵活电路表达，如 Permutation、Lookup 优化。

2. 算法复杂度

• 证明生成：O(n) 量级，其中n是电路门数；
• 验证：需要若干次配对 + 多项式承诺检查，通常极短时间内完成。

3. 安全性

• 依赖：Pairing（如 BLS12-381）或KZG多项式承诺；
• 可信设置：可一次性多方仪式，供不同电路反复使用；
• 量子威胁：曲线离散对数若被攻破，即面临安全风险。

4. 应用场景

• Layer2 zk-Rollup：zkSync、Polygon zkEVM、Scroll 等大量采用 Plonk；
• 隐私协议：对灵活电路/隐私交易做统一证明；
• 大规模DApp：无需频繁重新仪式、开发门槛相对较低。

九、总结

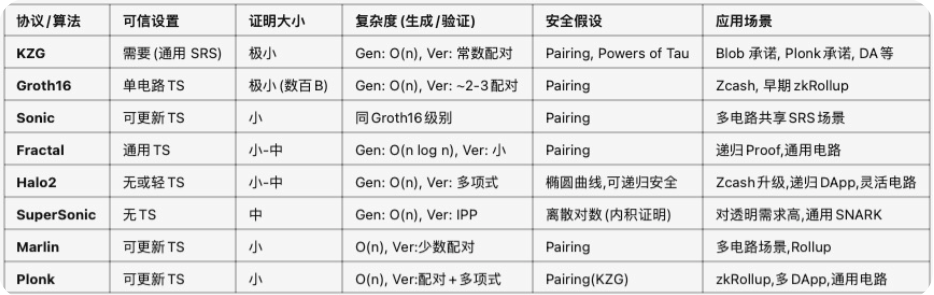KZG主要提供多项式承诺能力，被广泛用作基础模块；其余七者则是完整的SNARK协议（或其变体），多在证明体积、Trusted Setup、对电路的通用性等方面各有专长。

算法复杂度大体在生成过程是 O(n) 或 O(n \log n) 级别，验证环节多数仅需固定或较少的配对运算；

安全性大都依赖于当下的椭圆曲线离散对数难度，需进行可信设置（TS）或可更新仪式的方案不少。Halo2、SuperSonic等方案则尝试走无TS或轻TS路线；

应用场景围绕隐私交易、Layer2 扩容、通用计算、数据可用性等，开发者可根据需要在安全门槛、部署难度、电路规模、可信设置与验证效率之间做权衡。

在实际落地时，项目需结合业务规模、电路类型、对可信设置的容忍度、生态工具链支持等因素，挑选合适的 ZKP 协议。随着新一代算法与后量子安全研究的出现，这些协议也将持续迭代，为区块链与分布式系统的隐私与可扩容贡献更多力量。