在 Uniswap v4 中证明偿付能力：AMM 安全性的形式化验证

引言

像 Uniswap 这样的自动化做市商 (AMM) 是去中心化金融 (DeFi) 的基础，实现了无需信任的交易和流动性提供。流动性提供者 (LP) 的一个关键期望是他们始终可以提取资金，即使在像银行挤兑这样的最坏情况下也是如此。但是，我们如何正式证明 AMM 始终有足够的流动性来履行其义务呢？

本文深入探讨了 Uniswap v4 的流动性机制，并概述了一种正式的方法来证明其偿付能力。通过利用数学不变量和 SMT 求解器，我们展示了流动性是如何始终保持的，以及这些方法如何扩展到其他 DeFi 协议。

什么是 AMM？

AMM（自动化做市商）是一种去中心化交易所，促进流动性提供者和交易者之间的交易。流动性提供者提供可以交易的代币，以及他们希望允许交易的大致价格范围。

智能合约根据供应量自动调整交易价格。如果一种代币的供应量减少（因为交易者从合约中购买这种代币），价格就会上涨。如果供应量增加（因为交易者出售这种代币），价格就会下降。

流动性提供者从每笔交易中赚取费用，但他们不会影响其代币是被出售还是被购买。交易者向流动性提供者支付费用，并从其出售或购买订单的即时履行中获利。

AMM 的主要特点：

• 流动性提供者 (LP) 赚取交易费用，但无法直接控制交易。
• 交易者 以算法确定的价格立即交换代币。
• 智能合约 自动管理流动性，确保无需信任的执行。

AMM 中的偿付能力是什么？

偿付能力是指 AMM 合约中资产的可用性，特别是 LP 提供的流动性，以促进交易。要使 AMM 被认为是具有偿付能力的，它必须始终有足够的资金来满足所有 LP 的提款。

确保流动性：

• LP 收到代表他们在资金池中权益的凭证。
• 这些凭证允许 LP 随时提取其流动性份额。
• AMM 必须始终保持与这些义务相匹配的余额。

我们如何正式证明偿付能力？

一个应该始终成立的属性也称为不变量。在我们的例子中，不变量是合约有足够的资金来支付流动性提供者。为了证明一个不变量成立，可以单独查看任何函数，并论证该函数是否会违反该不变量，即是否存在从不变量成立的状态到不变量不成立的状态的转换。我们旨在证明的关键不变量是：

该合约始终有足够的资金来支付所有 LP。

为了验证这一点，我们分析智能合约中的每个函数，以确保它不会导致违反此不变量的状态。该方法包括：

1. 将代码翻译成数学公式。
2. 使用 SMT 求解器 来验证流动性在所有函数调用中是否得到保持。
3. 如果任何函数破坏了不变量，则生成反例。

为此，我们将函数的代码翻译成数学公式。然后，我们询问 SMT 求解器：对于所有可能的起始状态和所有函数参数，enough_funds@before && function → enough_funds@after holds 是否成立。我们对合约中的任何公共函数都这样做。如果公式始终为真，我们就从数学上证明了合约将始终有足够的资金。如果公式对于某些输入为假，SMT 求解器可以提供一个反例，解释在什么条件下可以违反不变量。

将其应用于 Uniswap v4

对于 Uniswap v4，交换函数至关重要，因为它基于内部流动性变量（pool.liquidity）计算代币数量。如果此值不正确，则计算出的代币数量可能不正确。我们的证明确保：

• 流动性始终正确地计算为所有活跃头寸的总和。
• 没有函数转换会破坏流动性不变量。

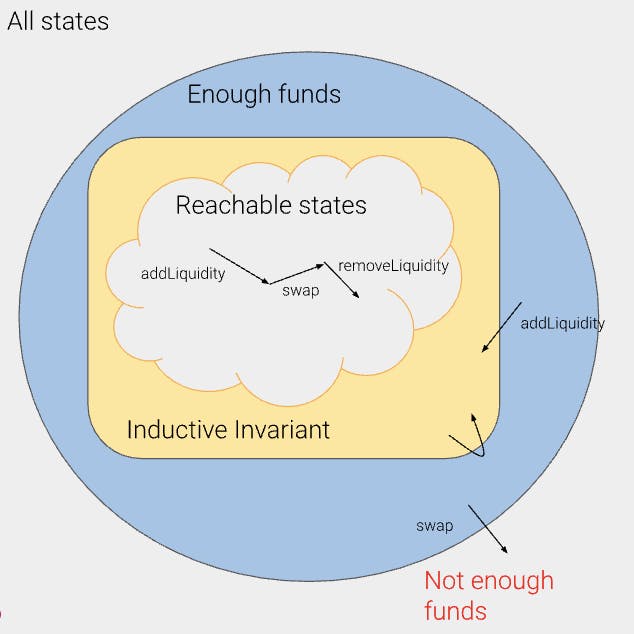
此图说明了 Uniswap PoolManager 的状态空间。蓝色圆圈表示合约保持足够资金（即保持偿付能力）的状态集。箭头表示因调用合约的公共函数而产生的潜在状态转换。云形包含可以通过这些转换从初始状态到达的所有状态。理想情况下，云将完全位于蓝色区域内，从而确保到达的每个状态都具有偿付能力。

但是，如图所示，某些转换（例如，当流动性计算错误时调用 swap 函数）会导致超出蓝色区域。通过引入额外的约束，我们可以定义一个较小的黄色区域，该区域仍然包含所有可到达的状态，并且对于源自该区域内状态的每个转换，都保持在该区域内。此黄色区域是一个归纳不变量，严格证明合约在每个可到达的状态中始终具有足够的资金。

我们将证明技术应用于一个具体的例子：Uniswap v4 池管理器。对于此合约，不变量 “足够资金” 可能会被交换操作违反。函数 swap 基于内部变量 pool.liquidity 计算代币数量。如果此变量的值错误，则 swap 计算的代币数量将是错误的。但是，在所有可到达的状态中，此变量都正确地计算为所有当前活跃头寸中的流动性总和。

一般来说，要证明一个不变量成立，可能需要同时证明更多的不变量，例如所有活跃头寸中的流动性之和等于 pool.liquidity。在 Uniswap 中，LP 可以通过提供 ticks 中的最小和最大交易价格来选择头寸活跃的价格范围。

为了证明这个新的不变量，即使头寸由于价格变化而被激活或停用，我们还需要证明第三个不变量，即对于任何 tick，ticks[tick].netLiquidity 等于从 tick 开始的头寸中的流动性之和与在 tick 结束的头寸中的流动性之和之间的差值。

一旦我们有足够的不变量，它们的组合就是一个归纳不变量：没有交易会导致从满足归纳不变量的状态转移到不满足归纳不变量的状态。此外，我们需要证明在调用构造函数后不变量成立。然后，我们有正式的证明，这些不变量对于所有可到达的状态都成立。

多少资金才算“足够”？

为了准确确定所需的资金，我们在 Uniswap v4 的合约中对其进行分类：

• 池中的流动性（交易对的代币储备）。
• LP 交易费用（已累积但尚未提取）。
• 协议费用（由 Uniswap DAO 收取）。
• ERC-6909 代币储备（支持合成代币）。
• 临时货币增量（待处理的交易或闪电贷）。
• 操作中的临时债务

最后两个条目是临时的，甚至可以是负数，这意味着合约在交易期间向用户提供闪电贷。临时债务仅在调用 post-swap 或 post-modify-liquidity Hook时存在。当调用 post-swap Hook时，交换已经发生，但尚未计为用户货币增量的变化，因为 post-swap Hook可能会通过给用户折扣或额外费用来修改代币数量。在 post-swap Hook返回后，货币增量会更新，临时债务被移除。post-modify-liquidity Hook的工作方式完全相同。

货币增量数据结构是瞬态的，仅在调用 unlock 函数解锁合约时存在。如果用户有待处理的闪电贷，则此增量为负数；如果用户收到了资金（通过移除流动性或交换），但尚未提取资金，则此增量为正数。锁定机制确保所有增量条目在交易结束时都为零。这确保用户偿还所有闪电贷并提取所有资金，或者为未提取的资金铸造 ERC-6909 代币。

ERC-6909 代币由合约中的真实 ERC-20 代币以 1:1 的比例支持。代币的 ID 是其 ERC-20 地址，代币由 Uniswap 核心合约本身铸造。它们可用于避免 ERC-20 代币的转账费用，方法是将所有 ERC-20 保留在 Uniswap 核心中，直到用户出售它们或使用它们来增加流动性。

最终的不变量方程确保：

我们可以引入一个 ghost 变量 并使用 hooks 或摘要来表示这些容器中的每一个。例如，_currency_delta 由库函数 CurrencyDelta.setDelta 更新。我们 summarize 这个函数并在一个 ghost 变量中保存所有账户和一个代币的所有 currency_delta_ 之和。

对于流动性，ghost 变量 _provided_liquidity[token]_ 是每个池的所有代币流动性之和。我们为每个池引入 ghost 变量来存储预期的代币数量。在下一节中，我们将解释如何计算此金额。

池流动性所需的代币

常数积池中代币对的流动性是所提供代币的几何平均值，即，如果 a 和 b 是 AMM 中代币对中的每个代币提供的代币数量，则流动性为 liq = √(a · b) 此外，以当前价格计算，两种代币中提供的流动性必须具有相同的估值，即 price = b/a。很容易从这些方程中推导出从流动性计算代币数量的方程：

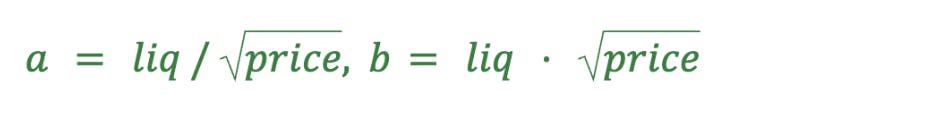
例子：

假设当前价格为 2500 美元/ETH，则价格的平方根为 50。

我们假设两种代币都有 18 位小数，因此 1 美元和 1 ETH 表示为 10^18。

提供 1 ETH 和 2500 美元，你可以获得 √(2500 · 10^36 ) = 50 · 10^18 的流动性。

ETH 的数量是通过将流动性除以当前价格的平方根得出的，从而得到 1 ETH，而美元的数量是通过将流动性乘以当前价格的平方根 (50) 得出的，从而得到 2500 美元。如果价格移动到 1600 美元/ETH（平方根价格为 40），则用户现在拥有 1.25 ETH 和 2000 美元。

获得的 ETH 和损失的美元是由于交易者将 ETH 出售为美元，这导致 ETH 价格下跌，也改变了 Uniswap 合约现在为该池持有的代币数量。这确保：

• 代币储备的比率与当前价格一致。
• 流动性池可以在保持偿付能力的同时促进交易。

集中流动性模型

LP 可以不为整个价格范围提供流动性，而是提供最小和最大价格范围。然后，他们不提供流动性的所有代币，而只提供在价格范围内交易的部分。只要价格超出价格范围，他们的头寸就会处于休眠状态，并且他们只拥有代币的一侧。

示例（续）：

让我们假设流动性提供者 (LP) 选择 1600 到 6400 美元/ETH 之间的价格范围，并提供 50 · 10^18 的流动性。在 1600 美元/ETH 的下限，如果没有集中流动性，LP 将拥有 1.25 ETH 和 2000 美元。相反，在 6400 美元/ETH 的上限，他们将持有 0.625 ETH 和 4000 美元。

LP 不需要投入 1 ETH 和 2500 美元的全部流动性金额，而只需要向合约输入 500 美元和 0.375 ETH。这是有策略地完成的，因此他们的余额在最低价格时减少到 0 美元，在最高价格时减少到 0 ETH。

如果价格超过 6400 美元/ETH，LP 将保留其头寸中的 2000 美元，而不保留 ETH。这实际上意味着用户以 4000 美元/ETH 的平均价格将其 0.375 ETH 出售为 1500 美元。LP 不需要额外的 2000 美元和 0.625 ETH，并且可以使用更少的资源来维持相同的流动性水平。这种策略称为集中流动性，因为用户仅在指定的交易范围内以减少的资本承诺获得相同的流动性。

有了集中流动性，单个头寸的代币数量的方程可以计算为：

为了避免计算平方根，Uniswap 合约将值 √price 存储在字段 cursqrtprice 中，并且计算 tick 价格的函数已经返回该价格的平方根。更准确地说，cursqrtprice 存储为定点数，即 2^96√price，并且始终为整数（swap 函数确保了这一点）。

一个棘手的问题是，我们在计算代币数量时必须避免舍入误差。如果存在舍入误差，任何价格变化都会增加更多的舍入误差，如果存在许多小头寸，这可能会使所需的代币数量增加多个代币。因此，当进行交换时，舍入误差可能会破坏不变量。

为了避免舍入误差，第一个技巧是将所有价格表示为它们的平方根，如上所述，因此不存在舍入误差。此外，我们不存储 a 和 b，而是将数量乘以 superprecision，这是一个非常大的数字，可以被低于 2^256 的任何数字整除。我们可以这样做，因为 CVL 中的 ghost 变量是没有限制的整数，并且可以任意大。通过将数量乘以这个大数字，我们确保 a*superprecision 始终是一个整数，从而消除了舍入误差的可能性。对于求解器，我们可以保持 superprecision 符号化，这样我们就不必写下这个数字。

处理舍入误差

计算舍入误差会导致流动性计算的差异。为了抵消这一点：

• 流动性值存储为高精度整数。
• 通过 ghost 变量和使用无界整数的符号计算，规范中没有舍入误差。

ERC-20 注意事项

Uniswap 中 ERC-20 代币的假设和要求

Uniswap 可以与任何 ERC-20 代币一起使用，但只有对于遵循特定规则的代币才能确保偿付能力：

• balanceOf() 没有副作用，仅查询账户余额。
• 账户余额只能由 owner 和 approved spenders 减少。
• 余额仅在调用代币的 transfer/transferFrom 函数时减少。
• 支出者只能由所有者批准，并且只能通过调用 approve 来批准。
• 函数 transfer(receiver, amount) 将发送者的余额减少确切的指定金额。
• 如果发送者有足够的余额，函数 transfer 不会 revert。

重要注意事项

• 在某些情况下，一些常用的代币并不完全满足这些假设。例如，类似于 stETH 的 rebasing 代币不受 Uniswap v4 的支持 —— 使用它们可能会导致资金损失 —— 而 Synthetix 类似于 Celo，并且在最终版本的 Uniswap v4 中受到技术支持。但是，我们的证明不包括它。
• 最后，USDC 有一个黑名单功能，理论上可能会阻止 Uniswap 合约向流动性提供者支付款项；但是，这种情况被广泛认为极不可能发生。
• AMM 流动性的证明不能防止所有损失。例如，如果代币收取费用，用户可能会收到少于转移的代币。
• 对于审计师在 24 年 8 月在 Celo 等链上提供的 Uniswap v4 版本，代币必须是 non-double-entry breaks，其中原生代币具有 ERC-20 镜像代币。最终版本的 Uniswap v4 修复了此问题。

结论

正式证明像 Uniswap v4 这样的 AMM 中的偿付能力可以提高安全性并增强用户信任。通过利用数学证明和自动化求解器，我们：

• 确保 AMM 在所有条件下都保持偿付能力。
• 识别并减轻潜在的舍入误差和代币不一致性。没有发现新的舍入问题。
• 通过严格的验证方法加强 DeFi 安全性。

DeFi 生态系统可以通过采用形式化验证技术来最大限度地减少智能合约漏洞，从而为更强大、更具弹性的金融基础设施铺平道路。

立即获取你的 Uniswap v4 审计！通过形式化验证审计确保你的 Uniswap v4 hook 实现的安全性。联系 Certora 以获取你的 Uniswap v4 hooks 的全面智能合约审计，并立即对你的合约进行形式化验证。

• 原文链接： certora.com/blog/proving...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～