完全递归 SNARK 电路 -“边玩边赚”的救星 - zk-s[nt]arks
- 以太坊中文
- 发布于 2024-01-24 11:21
- 阅读 950
本文探讨了使用零知识证明(ZK)技术在区块链游戏中的应用,重点介绍了递归zkSNARKs的技术背景及其在提升游戏性能、隐私性和信任度方面的作用。文章通过案例研究ZK-Hunt,展示了ZK技术如何在链上实现复杂的策略游戏机制和信息不对称,并讨论了ZK技术在资产隐藏、决策隐私和进度保密等方面的创新应用。
在“边玩边赚”的概念中,玩家希望在享受游戏的同时获得利润。然而,GameFi 受限于高昂的 GAS 成本和欠发达的区块链游戏生态系统,由于安全性和透明度问题,导致在获得玩家认可方面面临挑战。这推动 GameFi 不断优化经济模型和盈利机制,缩短了盈利周期,并可能最终导致崩溃。在新周期中,L2、跨链游戏引擎和 ZK 技术的广泛采用将为用户带来链上隐私和更复杂的链上游戏机制。这解决了性能、隐私和信任问题,将重点从庞氏骗局转向更值得信赖和更复杂的链上游戏。应用层 ZK 技术使游戏开发者能够轻松创建专为交互式隐私场景定制的链上战略游戏,为复杂且值得信赖的(链上)游戏场景带来新的可能性。 Salus 将在本文中讨论新的应用层 ZK 技术如何协助创新游戏场景的开发。
技术背景:递归 zkSNARK 的出现
zk-SNARK 是一种加密证明系统,其中证明者可以证明拥有某些信息而不泄露它,并且证明者和验证者之间没有交互。
递归 zk-SNARK 意味着开发者可以在一个 zk-SNARK 证明中验证另一个 zk-SNARK 证明,并生成 zk-SNARK 证明的声明。递归允许 zk-SNARK 证明者将更多的知识压缩到他们的证明中,同时保持简洁,并且递归验证过程不会显著减慢速度。
与常规 zk-SNARK 相比,递归 zk-SNARK 通过允许将多个证明压缩成一个单一证明,从而提供增强的可扩展性和效率。这种递归组合减少了复杂或多步骤过程的计算负载和证明大小,使其特别有益于像区块链游戏这样的应用程序,这些应用程序涉及大量的交互和交易。这将为用户和开发者带来更高的性能和更低的成本。
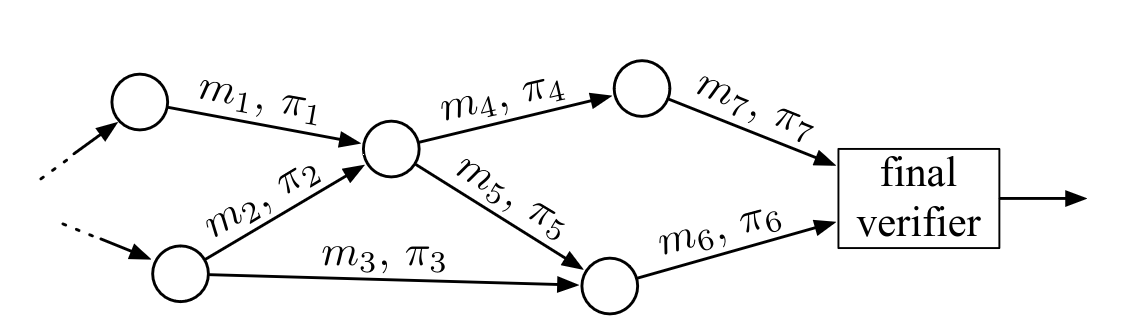
图片来源: 大规模共识的签名合并
递归 SNARK 解锁新的应用层面属性
压缩
递归 zkSNARK 允许证明者将“更多知识”放入证明中,同时确保验证者仍然可以在恒定或多次对数时间内验证这些证明。使用递归 ZK SNARK 作为信息的“rollup”,可以独立地“rollup”比最大的(非递归)电路可以处理的更多的计算。
可组合性
借助递归 SNARK,创建证明链是可行的,其中在每个步骤中,证明都会传递给新的参与者。每个参与者都将自己的知识声明添加到其中,而无需了解链中其他部分的详细信息。这种可组合性方面允许顺序构建证明,其中每个参与者以增量方式贡献,同时保持整体证明结构的完整性和机密性。
递归 SNARK 的实现。
通常,有两种方法来实现完全递归的 SNARK:
-
使用配对友好椭圆曲线的循环*:此方法涉及找到两个配对友好的椭圆曲线,使得一条曲线的阶等于另一条曲线的域大小。这通过利用这些曲线的属性来创建一个有效的递归。然而,找到既满足配对友好又满足循环属性的曲线具有挑战性,这仍然是一个持续研究的领域。
-
用单个配对友好曲线强制完成:第二种方法更简单,涉及在证明系统本身中简单地实现单个配对友好曲线的椭圆曲线运算。此方法不依赖于查找具有特定属性的一对曲线,而是在单条曲线的约束下工作。
关于第一种方法,配对友好椭圆曲线循环的概念定义如下:
定义 1:椭圆曲线循环是一系列定义在有限域上的椭圆曲线,其中一条曲线上的点数循环地等于定义下一条曲线的域的大小。椭圆曲线的 m 循环是 m 个不同的椭圆曲线 \frac{E_1}{F_{q1}},…, \frac{E_m}{F_{qm}} 的列表,其中 q_1,...,q_m 是素数,使得这些曲线上的点数满足
\#E_1(F_{q1})=q_2, ... ,\# E_i(F_{qi})=q_{i+1}, ... ,\#E_m(F_{qm})=q_1
高效的 zkSNARK 构造是通过配对友好的椭圆曲线获得的,而方程中的循环条件使其能够进行递归组合,同时避免了跨不同特征域的昂贵的模运算。
定义 2:配对友好的椭圆曲线 m 循环是一个 m 循环,使得循环中的每个椭圆曲线都是普通的并且具有较小的嵌入度。
第二种方法是强制完成,并且简单地在证明系统本身中实现单个友好曲线对上的椭圆曲线算术。你可以将配对电路移植到 BN254 曲线,然后在 Circom 中组装一个 growth 验证器。
例如,Groth16 证明系统具有一个两阶段的可信设置,其中第二阶段是特定于电路的。这意味着当你在 SNARK 内部验证证明时,它将需要一个独立于外部 SNARK 的可信设置。
因此,递归 groth16 SNARK 最合适的应用程序是那些递归到自身的应用程序,这意味着在电路内验证的证明是电路本身的证明。这意味着我们只需要执行一次可信设置。自递归 SNARK 的概念如下图所示:
SNARK 自递归 图片来源: 0xPARC
在每个步骤中,你都有一个电路来证明计算 A_i,A_{i+1}… 的有效性(可能 i 作为 SNARK 的公开输入),并且在第 i 个这样的证明中,你验证另一个证明,显示计算 A_{i+1},A_{i+2}… 以及步骤 Ai 的有效性。在每次递归中,你的 SNARK 电路将保持不变。例如,在 Isokratia 的情况下,每个 Ai 都是 ECDSA 签名验证。
总而言之,递归 zkSNARK 提供增强的可扩展性:它们减少了多步骤游戏或操作所需的数据和计算,使其在链上更可行,并确保复杂的游戏逻辑和状态转换能够快速安全地进行验证。
案例研究:ZK-Hunt 及其影响
ZK-Hunt 是一款基于区块链的 RTS 风格的 PvP 游戏,它探索了使用 ZK 技术来实现复杂的链上游戏机制和信息不对称。ZK-Hunt 允许玩家完全私密地执行操作,从而能够在不泄露任何底层数据的情况下验证每个操作。
在平原上移动是公开的,这体现在玩家 B 可以看到玩家 A 在移动时的位置更新。进入丛林也是公开的,但在丛林中移动是私密的,这样玩家 A 就会失去对玩家 B 在丛林中的位置的跟踪,并且只能模拟一组不断增长的潜在位置,这些位置用问号显示。退出丛林回到平原又是公开的,因此潜在位置的集合会崩溃。
这种信息隐藏行为是 ZK Hunt 的基础;单位具有一种状态(它们的位置),可以根据游戏中的动作从公共状态切换到私有状态,然后再切换回来。这增强了游戏玩法的战略深度。
ZK Hunt 中的状态验证过程主要涉及以下步骤:
- 在本地更新私有状态:从 S_{i-1} 过渡到 S_i(从公共状态切换到私有状态,反之亦然)。
- 生成有效状态转换的证明:利用 S_{i-1} 和 S_i(以及先前的承诺 C_{i-1},来生成新的承诺 C_i)。
- 提交证明以进行链上验证(合约提供承诺 C_{i-1} 的值,以确保正确生成证明)。
- 更新链上承诺(存储 C_i,以便可以在验证下一个转换时将其用作 C_{i-1})。
承诺 是一种工具,ZK 证明可以使用它来验证用户先前“承诺”的某些私有状态,而无需向验证者透露该状态。用户提供承诺 C 作为证明的公共输入,并提供私有状态 s 作为私有输入。该证明在内部计算 s 将产生的承诺,并检查它是否与 C 匹配:
template Example() {
signal input state; // 私有的
signal input commitment; // 公开的
// 根据“状态”计算 poseidon 哈希承诺
signal result <== Poseidon(1)([state]);
result === commitment;
// 电路的其余部分现在可以信任“状态”的有效性
...
}
component main {public [commitment]} = Example();虽然验证 ZK 证明的成本被认为是恒定的(至少对于某些证明系统,如 Groth16),但实际上,这种验证成本会随着公共输入的数量而增加,这在链上验证期间可能非常重要。同时,ZK Hunt 采用 Poseidon 哈希 作为其承诺方案,因为它与其他常见的哈希函数相比,在电路中计算起来效率更高,每个消息位需要更少的约束。如果私有状态是从足够大的范围内随机选择的值(例如私钥或随机种子),那么简单地获取此值的哈希就足以作为承诺。
通过类似的 ZK 技术可以实现许多其他游戏创新场景,例如资产隐藏、决策隐私和进度保密。
资产隐藏: 在设置和忘记纸牌游戏中,玩家可以使用零知识证明来隐藏他们的手牌,并且仅在打牌时显示必要的信息。
决策隐私: 在策略游戏中,玩家可以秘密地选择他们的下一步行动或分配资源,并且这些选择仅在特定时间点或由游戏逻辑触发时才会公开。
进度保密性: 在冒险或角色扮演游戏中,玩家可以完成任务或获得成就,而其他人不知道他们究竟完成了什么,从而保持一种惊喜或竞争秘密的元素。
通过采用零知识证明技术,ZK Hunt 允许玩家在保持隐私的同时进行游戏。 这不仅是一项技术创新,也是链上游戏规则的改变。通过这种方式,游戏操作在经过验证的同时不会泄露敏感数据,从而增强了策略的隐蔽性,并丰富了游戏的策略深度和惊喜元素。
如果你有兴趣将 ZK 技术集成到链上游戏中以增强隐私、可扩展性并实现游戏创新,Salus 提供端到端的 ZK 服务和综合解决方案。通过与我们合作,你可以探索 ZK 技术在游戏领域的广泛应用,为玩家提供更丰富、更安全、更具战略性的游戏体验。
- 原文链接: ethresear.ch/t/completel...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 后量子时代,我们如何保护隐私 227 浏览
- 关于伊朗监控影响的好文章 200 浏览
- ZK编年史:哈希登场 189 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 388 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 310 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 410 浏览
- Zcash:比特币遗忘的隐私 450 浏览
- 以太坊应该停止担心扩展性,去做人们想要的东西 385 浏览
- ZK编年史:计算模型 324 浏览
- lambdaworks 2026 年更新路线图和优先级 391 浏览
- 电子现金与隐私性 484 浏览
- 2026年构建机构级DeFi平台真正需要什么 951 浏览
 1124×336 18.2 KB
1124×336 18.2 KB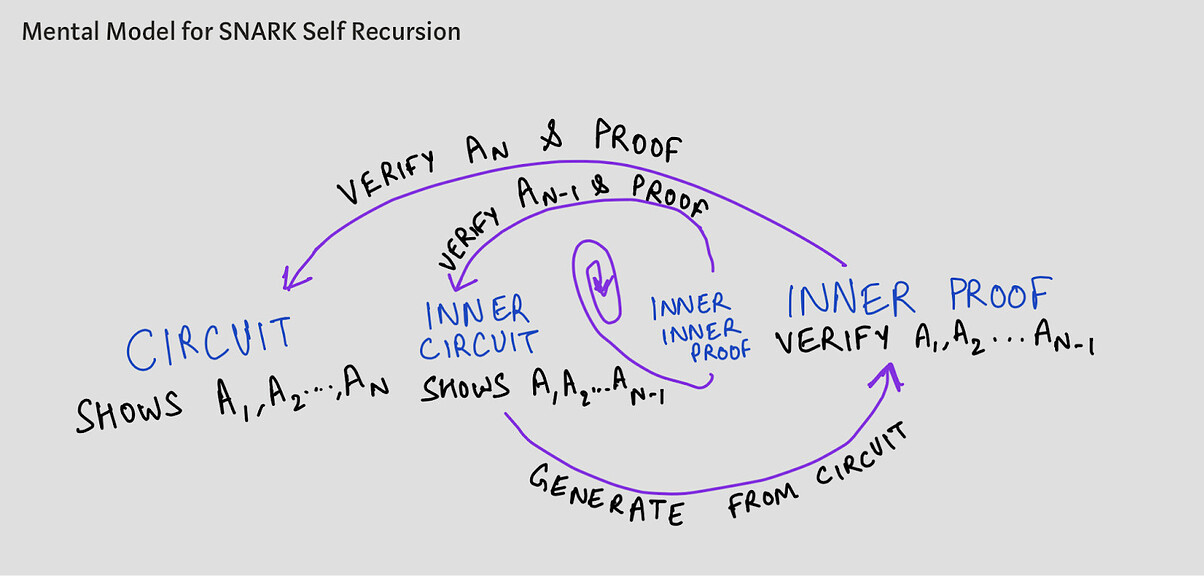 1600×765 122 KB
1600×765 122 KB 929×538 7.96 KB
929×538 7.96 KB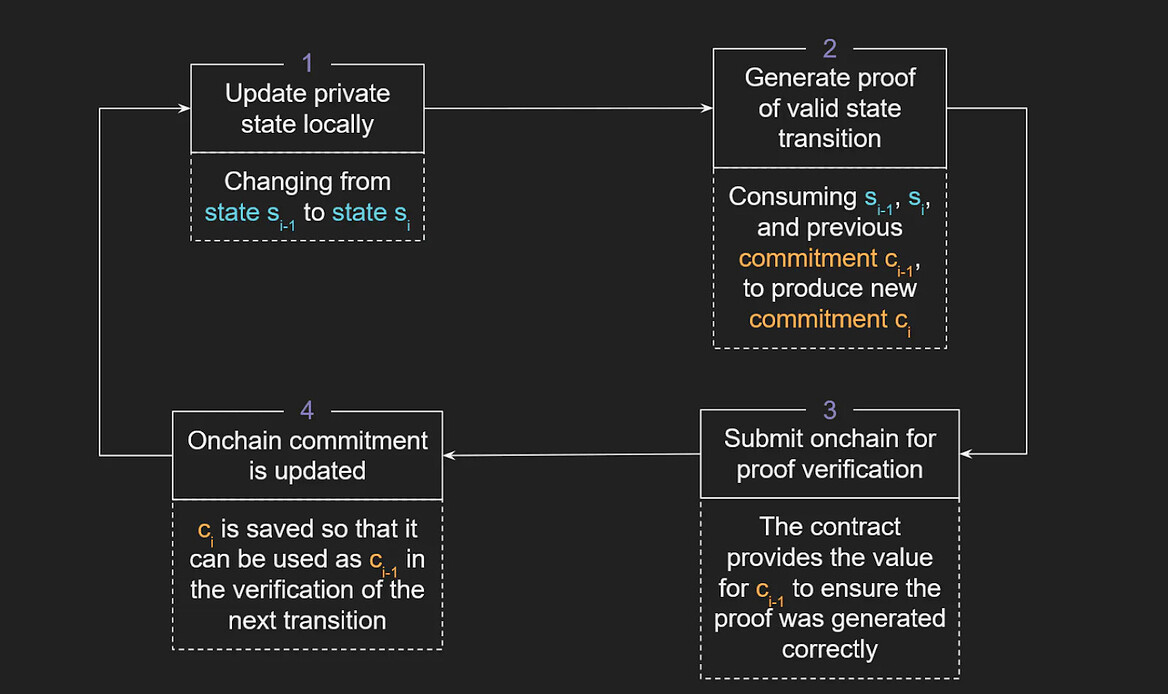 1600×951 147 KB
1600×951 147 KB
