无状态区块链的不可能性

随着区块链的发展，为了支持更多的用户和更频繁的交易，验证者存储的用于验证交易的信息量（“状态”）也在增长。例如，在比特币中，状态由一组未花费的交易输出（UTXO）组成。在以太坊中，状态由每个账户的账户余额以及每个智能合约的代码和存储组成。

对于拥有足够账户或UTXO以支持相当一部分人真正日常交易的区块链来说，这种存储负担将变得笨重，使得成为验证者变得困难，并对去中心化构成威胁。人们很想求助于密码学作为解决方案，在密码学中，诸如Merkle树和零知识证明之类的工具已经帮助我们实现了以前认为不可能的事情。

这正是“无状态区块链”的目标。但是，尽管对它们进行了大量工作，但它们仍然远未实用。但事实证明，这种进展的滞后是内在的——这些构造与实用性之间的差距永远无法弥合。我们最近的工作表明，无论多么巧妙的无状态区块链方案，如果没有额外的状态管理措施，都将永远不可行。正如我们在本文结尾处所示，不过，这种不可能的结果不应该令人沮丧。

无状态的状态

今天，状态很大，但可以管理。例如，比特币节点存储约 7 GB 的数据，以太坊节点存储约 650 GB 的数据。但是，完整节点的这种存储负担大致随链的吞吐量（每秒交易数或TPS）线性增加，而今天的吞吐量低得令人无法接受。按照当前的设计，真正支持日常交易（数万到数十万TPS）所需的状态将变得笨重，需要数TB甚至PB的存储空间。

这促使人们寻找技术方法来大幅减少验证者所需的状态量。圣杯是无状态区块链，它要求验证者仅存储恒定大小的状态，而与交易吞吐量无关。（这个术语实际上用词不当：仍然存在状态，只是它足够小，可以在任何未来的吞吐量下使用——通常它的尺寸是恒定的。）如此小的存储需求将使运行验证者节点变得更加容易；乐观地认为，每个人都可以在他们的手机上运行节点。由于增加验证者的数量可以提高链的安全性，因此降低验证者的准入门槛非常重要。

尽管对无状态区块链进行了大量研究（例如，由Todd、Buterin、Boneh et al.、Srinivasan et al.），但它们远未实用，据我们所知，没有一个被部署。所有已知的无状态区块链的根本问题是，它们需要用户存储称为见证(witnesses)的附加数据，以帮助验证者验证涉及其帐户的交易。例如，此见证可能是 Merkle 包含证明，表明用户的帐户及其余额包含在全局状态承诺中。当用户进行交易时，他们会将此见证提交给验证者，表明他们的帐户有足够的余额。

与存储永远不需要更改的私钥不同，这些见证会经常更改，即使对于不积极进行交易的用户也是如此，这给用户带来了不切实际的负担。同样，想象一下，如果你必须持续监控全球所有其他信用卡交易并相应地更新一些本地数据才能使用自己的信用卡。为了使区块链实用，用户必须能够保持离线状态，并且仅在提交交易时才与区块链进行交互。在许多情况下，例如硬件钱包，更新见证不仅不方便，而且不可能。

这导致我们提出一个自然的研究问题：我们能否构建一个不需要见证更新（或很少需要更新）的无状态区块链？为了回答这个问题，我们开发了一个新的理论框架（可撤销证明系统），该框架概括了无状态区块链。使用此框架，我们证明了一个结论性的不可能结果：简洁的全局状态和频繁的见证更新之间的这种权衡是根本性的。我们的证明技术是信息论的，这意味着未来的计算机将没有足够的能力来解决这个问题：无状态区块链构造与实用性之间的差距将永远无法弥合。

我们研究的背景

为了帮助建立对我们不可能结果的直觉，我们将首先描述使用Merkle树的无状态区块链的自然但效率低下的构造。我们的目标是让验证者确定用户提交的交易是否有效——例如，用户是否有足够的账户余额进行交易。在无状态区块链方案中，验证者存储一个恒定大小的状态。当用户进行交易时，他们必须在其交易中包含一个见证。验证者可以使用当前状态和用户提交的（交易，见证）对来验证该用户是否有足够的账户余额来进行交易。

我们首先构造一棵 Merkle 树，其中每个（帐户 ID，余额）对（a，b）都包含为叶子。验证者存储的恒定大小的状态 V 是这棵树的根，它充当帐户-余额对集合的承诺。每个用户将其（帐户 ID，余额）对的 Merkle 包含证明保持为其见证。叶子（a，b）的 Merkle 包含证明由其到树的根的路径上的伙伴节点（v 1，…，vk）组成。给定由帐户 a 和声称的余额 b 的用户进行的交易，验证者可以通过针对其当前状态 V 检查（a，b）的证明（v 1，…，vk）来检查 b 确实是帐户 a 的余额。如果是这样，验证者将执行交易并且必须相应地更新账户的余额。Merkle 树的一个方便的属性是，给定叶子的 Merkle 包含证明，可以很容易地计算出更改该叶子时产生的根。换句话说，验证者可以很容易地计算出更新后的状态 V’，该状态捕获了执行交易后账户 a 的新余额。

这个 Merkle 树方案有两个主要的缺点。首先，用户的见证相对较大，以系统中帐户总数的对数形式增长。理想情况下，它们应该是固定大小的，我们可以使用诸如RSA 累加器之类的方案来实现这一点（由 Boneh et al 在无状态区块链的上下文中研究）。

第二个缺点更难避免：每当任何其他用户进行交易时，账户-余额对的证明都会发生变化。回想一下，叶子的证明由从该叶子到树的根的路径上的伙伴节点组成。如果任何其他叶子发生变化，则其中一个节点也会发生变化，这在实践中提出了一个问题。大多数区块链用户希望将他们的币被动地保存在钱包中，并且仅在他们想要进行交易时才上线。然而，实际上，在这个无状态区块链中，用户将不得不不断监控其他所有人的交易以保持他们的见证是最新的。（虽然第三方可以代表用户进行此监控，但这偏离了标准的无状态区块链模型。我们将在本文末尾讨论这个问题。）实际上，这对无状态区块链来说是一个无法克服的挑战，给用户带来了沉重的负担。

我们的结果：无状态性是不可能的

这种现象并非特定于此 Merkle 树构造——所有已知的无状态区块链方案都需要用户频繁更新他们的见证，我们在此演示了这一点。更准确地说，我们表明必须更新见证的用户数量大致随所有用户进行的交易总数线性增长。

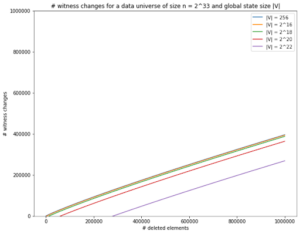
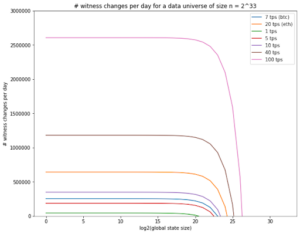
这意味着即使是用户 Alice 未进行任何交易，她的见证也可能需要随着其他用户的交易而更改。只要验证者存储的简洁状态太小而无法捕获完整状态（即，所有帐户余额的集合），增加简洁状态大小的帮助就很小。我们在下面绘制了由我们的定理暗示的这种关系，以及各种吞吐量的区块链每天所需的见证更改次数。这些图显示了最佳可能的无状态区块链需要更改见证的次数。在这里，数据世界指的是帐户总数（在帐户模型中）或 UTXO（在 UTXO 模型中）。

我们证明的核心是信息论的论点。信息论的一个核心原则，由 Claude Shannon 正式确定，是如果 Alice 从大小为 2 的集合中随机选择一个对象 n 并且想要告诉 Bob 她选择哪个对象，她必须向他发送至少 n 位。如果存在一个无状态区块链方案，其中用户不经常更新他们的见证，Alice 可以使用少于 n 位的位数告诉 Bob 她选择哪个对象——Shannon 表明这是不可能的。因此，不可能存在这样的无状态区块链。

为简单起见，我们将在此处描述一个稍微弱一点的语句的证明：不存在用户从不需要更新其见证的无状态区块链。关键思想是 Alice 使用无状态区块链方案来将她的消息编码给 Bob。最初，Alice 和 Bob 都知道所有 n 个用户的完整帐户-余额对集合。假设每个帐户至少有一个币。Alice 和 Bob 也都知道无状态区块链的简洁状态 V 和所有帐户-余额对的见证 wi（ai，bi）。Alice 和 Bob 还就消息和帐户集之间的映射达成了一致。Alice 将选择一组对应于她的消息的帐户 A，然后她将从这些帐户中花费币。她将使用无状态区块链来告知 Bob 她选择了哪个集合，并且他可以从该集合中了解到她的消息是什么。

编码： Alice 从 A 中的每个帐户中花费一个币。使用无状态区块链方案，Alice 计算出更新后的状态 V’ 并将 V’ 发送给 Bob。

解码： 对于每个 i，Bob 检查 Verify( wi,( ai, bi)) . Bob 输出帐户集 B，使得 Verify( wi, ( ai, bi)) = false.

Bob 成功输出了与 Alice 选择的集合相同的集合：B = A. 首先，观察到，如果 Alice 从帐户 ai 花费了一个币，则不应再接受其旧余额的见证——否则，Alice 将能够双重花费。因此，对于 A 中的每个帐户 ai，Verify( wi, ( ai, bi)) = false, 并且 Bob 会将此帐户包含在 B. 中。另一方面，Bob 永远不会在 B 中包含 Alice 没有从中花费币的帐户，因为这些帐户的余额保持不变，并且（回想一下我们着手证明的放宽语句）它们的见证永远不会更改。因此，B 完全等于 A。

最后，我们通过计算 Alice 应该发送给 Bob 的位数来得出我们的矛盾。她可能选择了 2 n 个可能的帐户子集，因此根据 Shannon 定律，她应该至少向 Bob 发送 n 位。但是，她只发送了恒定大小的状态 V’，它比 n 位短得多。

（熟悉密码学的读者可能会注意到，我们在这里忽略了一些细节；例如，Bob 的解码可能会以可忽略的概率失败。我们的论文 包含了完整的证明。）

虽然我们用无状态区块链来描述我们的证明，但 Alice 和 Bob 可以使用各种其他经过身份验证的数据结构（包括累加器、矢量承诺和经过身份验证的字典）来执行类似的过于有效的通信。我们使用一种称为可撤销证明系统的新抽象来形式化此类数据结构。

结果的含义

我们的结果表明，你无法“用密码学消除状态”——没有灵丹妙药式的承诺方案允许我们构建一个用户从不需要更新其见证的无状态区块链。状态不会消失，而是从验证者转移出去，并以频繁的见证更新的形式推给用户。

确实存在几种偏离严格的无状态区块链模型的其他有希望的解决方案。此模型的一种自然放松是允许第三方（既不是用户也不是验证者）负责存储完整状态。此方称为证明服务节点（由 Srinivasan et al. 进行了最严格的检查），它使用完整状态代表用户生成最新的见证。然后，用户可以使用这些见证像在常规的无状态区块链中一样进行交易，其中验证者仍然只存储简洁的状态。该系统的激励机制，尤其是用户如何补偿证明服务节点，是一个有趣的开放研究方向。

虽然到目前为止我们的讨论主要集中在 L1 区块链上，但我们的结果也对像 rollup 服务器这样的 L2 系统产生了影响。Rollup（无论是乐观的还是 ZK）通常采用大型状态，并使用存储在 L1 上的小值来承诺它。此状态包括 L2 上每个用户的帐户。我们希望这些用户能够通过发布其当前帐户余额的见证，直接在 L1 上提取资金（无需 L2 服务器的合作）。此设置也是我们模型中的可撤销证明系统的一个实例。事实上，有人可能会争辩说，无状态区块链已经在实践中实现了，以 L2 rollups 的形式。

但不幸的是，这意味着我们的不可能结果直接适用。用户的 rollup 提款见证必须频繁更改，否则几乎整个 L2 状态都必须写入 L1。因此，今天的 rollups 通常假设一个数据可用性委员会（有时称为“validium”），它类似于“证明服务节点”，可以帮助用户在准备提款时计算新的见证。以太坊文档 中对用户的警告——“如果无法访问交易数据，用户将无法计算证明资金所有权和执行提款所需的 Merkle 证明。” ——将始终适用。

\*\*\*

随着区块链系统的发展，开发更有效的方式来管理区块链状态将变得更加重要。虽然我们排除无状态区块链的结果可能看起来是负面的，但不可能的结果对区块链设计者很有用，因为它们告诉我们将研究重点放在其他地方，理想情况下可以帮助我们更快地找到可行的解决方案。 有关更多详细信息，你可以阅读完整论文 并观看 Miranda 在 a16z 加密实验室研讨会系列中关于该论文的演示文稿。 Miranda Christ 是哥伦比亚大学计算机科学专业的博士生，她是理论小组的成员，也是总统研究员。她是 a16z 加密货币的 22 年夏季研究实习生。 Joseph Bonneau 是 a16z 加密货币的研究合伙人。他的研究重点是应用密码学和区块链安全。他曾在墨尔本大学、纽约大学、斯坦福大学和普林斯顿大学教授加密货币课程，并获得了剑桥大学计算机科学博士学位以及斯坦福大学的 BS/MS 学位。

• 原文链接： a16zcrypto.com/posts/art...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～