加密货币期权-1、正态分布与布朗运动
- lychunchun
- 发布于 2025-09-02 21:23
- 阅读 1187
blackscoles公式是为欧式期权定价的基本模型。在开始关于它的分析之前,我们看一个简单的分布函数-高斯分布,也叫正态分布。首先我们看下这个球粒沙漏,球粒沿着有多排钉子的直立板向下滚动,在每个点都有相同的概率向左或者向右移动。最后的形状如上图所示,当球粒足够多时,会呈现出完美的钟形曲线,
blackscoles公式是为欧式期权定价的基本模型。在开始关于它的分析之前,我们看一个简单的分布函数-高斯分布,也叫正态分布。 首先我们看下这个球粒沙漏,球粒沿着有多排钉子的直立板向下滚动,在每个点都有相同的概率向左或者向右移动。

 最后的形状如上图所示,当球粒足够多时,会呈现出完美的钟形曲线,也就是正态分布的函数曲线。
最后的形状如上图所示,当球粒足够多时,会呈现出完美的钟形曲线,也就是正态分布的函数曲线。


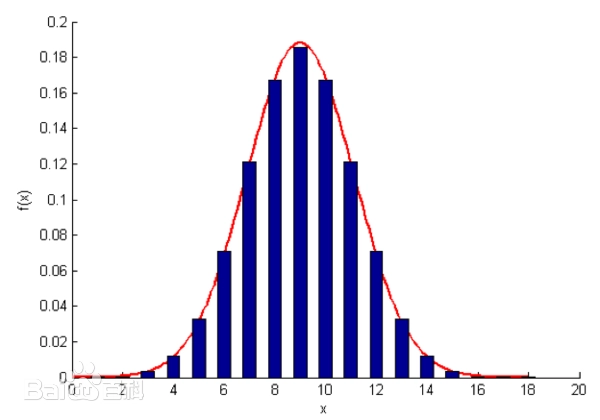
当正态分布函数中两个参数分别为0和1时,这个图像便为标准正态分布,它是沿着y轴呈左右对称。之所以会呈现出这种图形,沙粒运动时一个关键的原因在于,向左和向右运动的概率相同,都是1/2。
再看第二个例子,假设一个布朗粒子从x轴的原点出发,则布朗粒子在t时刻的位移x(t)是时间t的函数,x(t)的函数图像(质点位移轨迹)见图
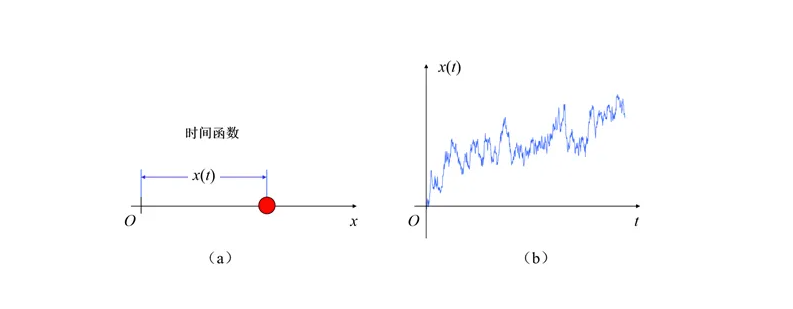
严格意义上来说,布朗粒子有比较严格的数学要求,在每个运动时间段,都有相同的概率向右和向左运动,这样一个描述位置和时间关系的随机函数x(t),叫做维纳运动,也叫标准布朗欲动。
当有大量的离子处于布朗运动的过程时,它的分布函数呈现为标准正态分布,但是对于单个粒子来说,它是一个随机过程。
粒子既有向左又有向右运动的可能,加密货币的价格是有可能涨也有可能跌,但现实情况是,加密货币涨和跌的概率不大可能是相等的。那么描述加密货币价格和时间的这个随机函数,它不大可能是一个布朗运动。 那么它是什么呢,一般说来,在研究过程中,我们叫它几何布朗运动。 它的运动呈现出一下模型
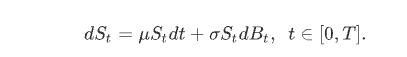
- 原创
- 学分: 20
- 分类: DeFi
- 标签:
点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ,好文好收益,欢迎正在阅读的你也加入。
0 条评论
请先 登录 后评论


