UniswapV1 自学系列 02 - 定价功能实现
- 青山
- 发布于 2025-09-20 20:25
- 阅读 810
在UniswapV1系列的第二篇文章中,我们将深入探讨去中心化交易所的核心机制:定价功能的设计与实现。
UniswapV1 自学系列 02 - 定价功能实现
在 UniswapV1 系列的第二篇文章中,我们将深入探讨去中心化交易所的核心机制:定价功能的设计与实现。
定价机制的思考
1.1 直观的定价思路
初学者可能会认为,去中心化交易所的价格计算就是简单的储备比例关系:

其中:
P_X表示代币X相对于代币Y的价格x和y分别表示两种代币的储备量
这种想法确实有其合理性。与中心化交易所不同,去中心化交易所合约无法获取外部价格信息,它们必须依据自身持有的资产储备来确定价格。从这个角度看,Exchange合约本身就扮演着价格预言机的角色。
1.2 简单定价函数的实现
让我们基于储备比例的思路,先实现一个简单的定价函数:
/**
* @dev 基于储备比例的简单定价函数
* @param inputReserve 输入代币的储备量
* @param outputReserve 输出代币的储备量
* @return 返回价格比例
*/
function getPrice(uint256 inputReserve, uint256 outputReserve)
public
pure
returns (uint256)
{
// 确保储备量不为零,避免除零错误
require(inputReserve > 0 && outputReserve > 0, "invalid reserves");
// 返回输入储备与输出储备的比例
return inputReserve / outputReserve;
}1.3 测试简单定价函数
让我们使用 Foundry 测试框架来验证定价函数的正确性:
// 在 ExchangeTest.t.sol 中添加测试函数
function testGetPriceSimpleImpl() public {
vm.startPrank(user);
// 1. 授权并添加流动性:2000个代币 + 1000个ETH
token.approve(address(exchange), 2000 ether);
exchange.addLiquidity{value: 1000 ether}(2000 ether);
// 2. 获取当前储备量
uint256 tokenReserve = exchange.getReserve();
uint256 etherReserve = address(exchange).balance;
// 3. 测试价格计算
// ETH相对于Token的价格(应该是0.5)
uint256 ethPerToken = exchange.getPrice(etherReserve, tokenReserve);
assertEq(ethPerToken, 0); // 注意:这里会失败!
// Token相对于ETH的价格(应该是2)
uint256 tokenPerEth = exchange.getPrice(tokenReserve, etherReserve);
assertEq(tokenPerEth, 2);
vm.stopPrank();
}forge test --match-test testGetPriceSimpleImpl -v2. 整数除法精度问题
2.1 问题分析
按照我们的预期,存入2000个代币和1000个ETH后,代币价格应该是0.5 ETH,ETH价格应该是2个代币。但是测试却失败了,显示代币价格为0。
根本原因:Solidity只支持整数运算,除法运算会自动向下取整。当计算 1000/2000 = 0.5 时,结果被截断为0!
2.2 精度优化方案
为了解决精度问题,我们需要引入放大因子:
/**
* @dev 改进的定价函数,使用1000倍放大因子提高精度
* @param inputReserve 输入代币的储备量
* @param outputReserve 输出代币的储备量
* @return 返回价格比例(放大1000倍)
*/
function getPrice(uint256 inputReserve, uint256 outputReserve)
public
pure
returns (uint256)
{
require(inputReserve > 0 && outputReserve > 0, "invalid reserves");
// 使用1000倍放大因子避免精度丢失
return (inputReserve * 1000) / outputReserve;
}2.3 更新后的测试
function testGetPriceWithPrecision() public {
vm.startPrank(user);
// 添加流动性:2000个代币 + 1000个ETH
token.approve(address(exchange), 2000 ether);
exchange.addLiquidity{value: 1000 ether}(2000 ether);
uint256 tokenReserve = exchange.getReserve();
uint256 etherReserve = address(exchange).balance;
// ETH相对于Token的价格:1000*1000/2000 = 500(表示0.5)
uint256 ethPerToken = exchange.getPrice(etherReserve, tokenReserve);
assertEq(ethPerToken, 500);
// Token相对于ETH的价格:2000*1000/1000 = 2000(表示2.0)
uint256 tokenPerEth = exchange.getPrice(tokenReserve, etherReserve);
assertEq(tokenPerEth, 2000);
vm.stopPrank();
}运行测试验证结果:
forge test --match-test testGetPriceWithPrecision -v现在价格计算正确了:1个代币 = 0.5 ETH,1个ETH = 2个代币。
3. 简单定价函数的致命缺陷
3.1 资金池枯竭问题
虽然价格计算看起来合理,但这个定价函数存在严重问题。假设有用户想要用全部的2000个代币换取ETH,按照当前价格,他们应该得到1000个ETH——这正好是合约中的全部ETH储备!
问题核心:这种定价机制会导致交易所资金完全枯竭,这显然不是我们期望的结果。
3.2 常数和公式的数学问题
这个定价函数实际上遵循的是常数和公式(Constant Sum Formula):
k = x + y(常数)从数学角度看,这个公式描述的是一条直线,它会与x轴和y轴相交。这意味着在某些情况下,储备量可能降至0,这正是导致资金池枯竭的根本原因。
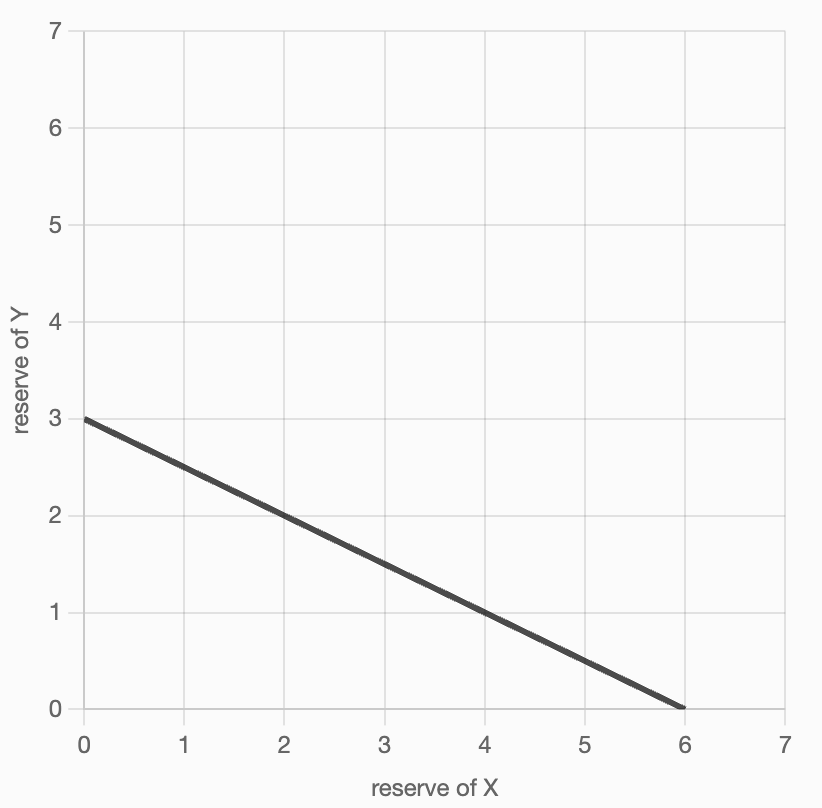
关键问题:直线函数允许任一储备量归零,这与去中心化交易所需要维持持续流动性的要求相矛盾。
4. 恒定乘积公式:正确的解决方案
4.1 UniswapV1的核心理念
Uniswap采用的是恒定乘积做市商(Constant Product Market Maker)机制,其数学基础是恒定乘积公式:
x × y = k(常数)其中:
x和y分别表示两种代币的储备量k是一个恒定的乘积值
这个公式是否能解决我们遇到的问题呢?让我们深入分析。
4.2 交易过程的数学建模
恒定乘积公式确保了无论储备量如何变化,乘积 k 始终保持不变。在每笔交易中:
- 用户投入
Δx数量的代币A - 获得
Δy数量的代币B - 交易后储备量变为
(x+Δx)和(y-Δy)
交易前后恒定乘积关系的数学表达:
(x + Δx)(y - Δy) = xy这个等式确保了交易前后乘积保持不变。
4.3 推导输出金额公式
通过对恒定乘积等式进行代数变换,我们可以求出输出金额 Δy:
展开:(x + Δx)(y - Δy) = xy
化简:xy - xΔy + yΔx - ΔxΔy = xy
消除xy:-xΔy + yΔx - ΔxΔy = 0
移项:xΔy + ΔxΔy = yΔx
提取Δy:Δy(x + Δx) = yΔx
求解:Δy = (yΔx) / (x + Δx)最终公式:
Δy = (输出储备 × 输入金额) / (输入储备 + 输入金额)这个公式有一个重要特性:输出金额现在取决于输入金额,而不仅仅是储备比例。
4.4 实现恒定乘积定价函数
现在我们基于恒定乘积公式来实现正确的定价函数。注意:我们现在处理的是具体的交易金额,而不是抽象的价格比例。
/**
* @dev 基于恒定乘积公式的金额计算函数
* @param inputAmount 用户输入的代币数量
* @param inputReserve 输入代币的当前储备量
* @param outputReserve 输出代币的当前储备量
* @return 用户能够获得的输出代币数量
*/
function getAmount(
uint256 inputAmount,
uint256 inputReserve,
uint256 outputReserve
) private pure returns (uint256) {
// 确保储备量和输入金额有效
require(inputReserve > 0 && outputReserve > 0, "invalid reserves");
require(inputAmount > 0, "invalid input amount");
// 应用恒定乘积公式:Δy = (yΔx) / (x + Δx)
return (inputAmount * outputReserve) / (inputReserve + inputAmount);
}4.5 高级封装函数
getAmount 是底层计算函数,我们将其设为私有。现在创建两个面向用户的高级函数,分别处理ETH→代币和代币→ETH的兑换:
/**
* @dev 计算用ETH购买代币的数量
* @param _ethSold 出售的ETH数量
* @return 能够获得的代币数量
*/
function getTokenAmount(uint256 _ethSold) public view returns (uint256) {
require(_ethSold > 0, "ETH amount too small");
uint256 tokenReserve = getReserve();
uint256 ethReserve = address(this).balance;
// 计算:用ETH买代币
return getAmount(_ethSold, ethReserve, tokenReserve);
}
/**
* @dev 计算用代币购买ETH的数量
* @param _tokenSold 出售的代币数量
* @return 能够获得的ETH数量
*/
function getEthAmount(uint256 _tokenSold) public view returns (uint256) {
require(_tokenSold > 0, "Token amount too small");
uint256 tokenReserve = getReserve();
uint256 ethReserve = address(this).balance;
// 计算:用代币买ETH
return getAmount(_tokenSold, tokenReserve, ethReserve);
}4.6 测试恒定乘积定价函数
让我们使用Foundry框架测试新的定价函数:
function testGetTokenAmount() public {
vm.startPrank(user);
// 1. 添加初始流动性:2000代币 + 1000ETH
token.approve(address(exchange), 2000 ether);
exchange.addLiquidity{value: 1000 ether}(2000 ether);
// 2. 测试用1个ETH购买代币
uint256 tokensOut = exchange.getTokenAmount(1 ether);
// 3. 验证结果(应约为1.998代币,略小于2代币)
assertEq(tokensOut, 1998001998001998001);
vm.stopPrank();
}
function testGetEthAmount() public {
vm.startPrank(user);
// 1. 添加初始流动性
token.approve(address(exchange), 2000 ether);
exchange.addLiquidity{value: 1000 ether}(2000 ether);
// 2. 测试用2个代币购买ETH
uint256 ethOut = exchange.getEthAmount(2 ether);
// 3. 验证结果(应约为0.999ETH,略小于1ETH)
assertEq(ethOut, 999000999000999000);
vm.stopPrank();
}运行测试:
forge test --match-test testGetTokenAmount -v
forge test --match-test testGetEthAmount -v5. 价格滑点机制分析
5.1 测试结果分析
测试结果显示:
- 1个ETH → 1.998个代币(而非2个)
- 2个代币 → 0.999个ETH(而非1个)
这些数值与简单比例计算的结果非常接近,但都略小一些。这种现象背后有重要的经济学原理。
5.2 双曲线特性的数学意义
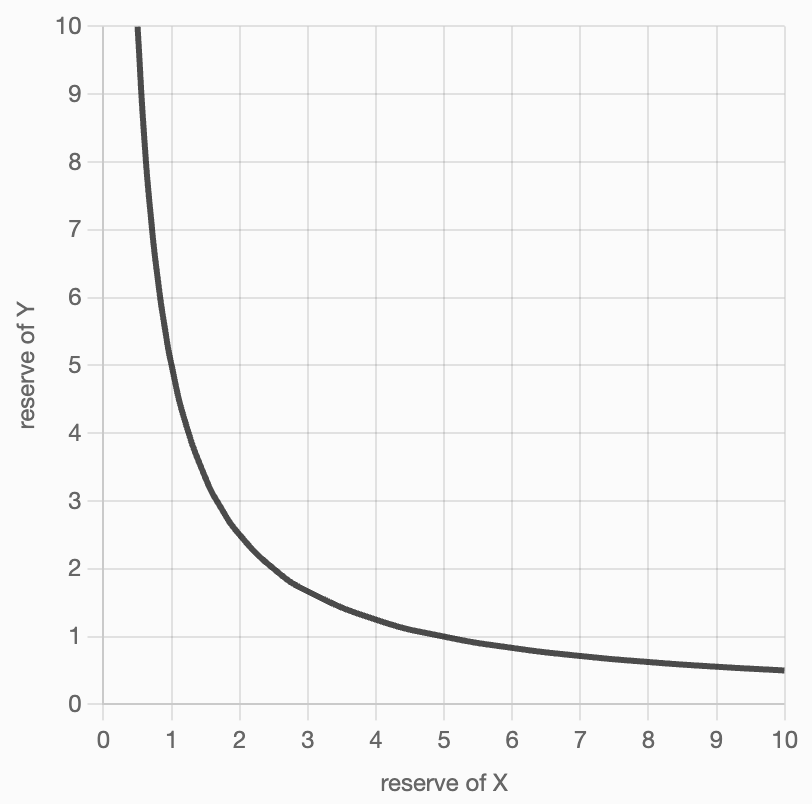
恒定乘积公式 xy = k 在数学上描述的是一条双曲线,这个几何特性具有重要意义:
关键特性:
- 永不归零:双曲线永远不会与x轴或y轴相交,这意味着储备量永远不会降至0
- 无限流动性:理论上储备是"无限"的,只是获取成本越来越高
- 自动平衡:系统会自动维持两种资产的平衡
5.3 价格滑点机制
价格滑点(Price Slippage)是AMM的核心特性:交易数量相对储备量越大,实际成交价格偏离理论价格越多。
这种机制有双重作用:
- 保护作用:防止大额交易瞬间抽干资金池
- 激励作用:鼓励套利者在价格偏离时进行反向操作,维持价格稳定
测试中出现的"收益略低"现象正体现了滑点机制的作用。虽然表面上看每笔交易都有"损失",但这个机制实际上:
- 防止枯竭:确保资金池不会被大额交易完全抽干
- 符合经济学:完美契合供求关系——需求越大,成本越高
- 维持稳定:通过价格调节机制维持市场平衡
这不是缺陷,而是精心设计的保护机制。
5.4 滑点效应的深度测试
让我们通过对比不同交易规模来直观感受滑点效应:
function testSlippageEffect() public {
vm.startPrank(user);
// 初始流动性:2000代币 + 1000ETH
token.approve(address(exchange), 2000 ether);
exchange.addLiquidity{value: 1000 ether}(2000 ether);
// 小额交易:1 ETH → ? 代币
uint256 tokens1 = exchange.getTokenAmount(1 ether);
assertEq(tokens1, 1998001998001998001); // 约1.998代币
// 中等交易:100 ETH → ? 代币
uint256 tokens100 = exchange.getTokenAmount(100 ether);
assertEq(tokens100, 181818181818181818181); // 约181.8代币(滑点显著)
// 大额交易:1000 ETH → ? 代币
uint256 tokens1000 = exchange.getTokenAmount(1000 ether);
console.log("tokens1000", tokens1000);
assertEq(tokens1000, 1000 ether); // 正好1000代币(接近极限)
vm.stopPrank();
}
function testReverseSlippage() public {
vm.startPrank(user);
// 初始流动性:2000代币 + 1000ETH
token.approve(address(exchange), 2000 ether);
exchange.addLiquidity{value: 1000 ether}(2000 ether);
// 小额:2 代币 → ? ETH
uint256 eth2 = exchange.getEthAmount(2 ether);
assertEq(eth2, 999000999000999000); // 约0.999 ETH
// 中等:100 代币 → ? ETH
uint256 eth100 = exchange.getEthAmount(100 ether);
assertEq(eth100, 47619047619047619047); // 约47.6 ETH
// 大额:2000 代币 → ? ETH
uint256 eth2000 = exchange.getEthAmount(2000 ether);
console.log("eth2000", eth2000);
assertEq(eth2000, 500 ether); // 正好500 ETH(一半储备)
vm.stopPrank();
}5.5 极限情况分析
从测试结果可以看出一个重要规律:当交易金额接近储备总量时,用户最多只能获得对应储备的50%。这是恒定乘积公式的数学特性决定的,确保了资金池永远不会完全枯竭。
6. 总结与思考
6.1 定价函数的演进
我们的定价函数经历了三个阶段:
-
简单比例:
价格 = 储备比例- 优点:直观易理解
- 缺点:会导致资金池枯竭
-
精度优化:引入放大因子解决整数除法问题
- 解决了计算精度问题
- 但仍然存在枯竭风险
-
恒定乘积:基于
xy = k的科学定价- 永不枯竭的数学保证
- 自带滑点保护机制
- 符合经济学原理
6.2 关键洞察
简单比例定价并非完全错误——当交易金额相对储备量很小时,它给出的价格是合理的。但要构建真正的AMM系统,我们需要更精密的恒定乘积机制。
这种渐进式的理解过程,正是学习UniswapV1原理的最佳路径:从直觉出发,发现问题,逐步优化,最终掌握核心机制的数学精髓。
技术要点回顾
- 恒定乘积公式:
x × y = k - 交易公式:
Δy = (yΔx) / (x + Δx) - 滑点保护:防止资金池枯竭的核心机制
- 双曲线特性:确保储备永不归零的数学基础
📚 项目仓库
完整项目代码请访问: https://github.com/RyanWeb31110/uniswapv1_tech
本系列文章是基于该项目的完整教学实现,欢迎克隆代码进行实践学习!
- 原创
- 学分: 7
- 分类: Uniswap
- 标签:

