Solana 60 天课程
生息代币第一部分
- RareSkills
- 发布于 2025-10-17 10:21
- 阅读 1268
本文深入探讨了 Solana Token-2022 中 interest-bearing 扩展的工作原理,该扩展允许 Token mint 自动累积利息,而无需链上余额更新。文章详细解释了利息计算模型,包括连续复利公式如何在链下计算利息,以及如何在钱包和应用程序中正确显示和处理这些余额。
Token-2022 的计息扩展功能允许 token mint 为该特定 mint 的所有 token 账户自动产生利息。它使用 mint 的链上配置中定义的年利率。
但是,此利息是一种计算视图:链上的实际 token 余额永远不会改变。相反,钱包和应用程序将连续复利公式应用于每个用户的链上余额,以计算其扣除应计利息后的余额。开发者可以将计算出的利息和链上余额合并为一个值或单独显示它们。
此扩展提供了用于计提利息的会计机制;它依赖于单独的 DeFi 应用程序来为利息提供经济支持。
在本文中,我们将分解计息扩展的架构,解释计算背后的数学原理,涵盖钱包兼容性,并通过一个使用 Anchor 的实际实现示例。
计息扩展架构
正如我们在 Token-2022 文章中讨论的那样,token 扩展是添加到 mint 或 token 账户的模块化功能。mint 账户的基本布局为 82 字节,token 账户的基本布局为 165 字节。扩展数据附加在这些基本大小之后,因此在创建 mint 或 token 账户之前,你必须分配等于基本大小加上任何已启用扩展大小的空间。
为计息扩展分配的空间存储扩展的数据,包括可以更新利率的授权账户字段。如果授权账户字段全为零,则将其视为 None,这意味着利率保持不变。在实践中,授权可以设置为 DeFi 应用程序,然后设置利率以反映应用程序中的实际经济活动。
除了授权字段之外,下面的 Rust 结构体(我们直接从扩展的源代码中获取)定义了完整的计息扩展数据:
- 初始化时间戳(
initialization_timestamp),用作所有利息计算的开始时间 - 自初始化以来直到上次更新利率时的平均利率(
pre_update_average_rate)。 - 上次利率变化时间戳(
last_update_timestamp),用于计算应计利息 - 自上次更新时间戳以来应用的当前利率(
current_rate)。
/// 年利率,以基点表示
pub type BasisPoints = PodI16;
const ONE_IN_BASIS_POINTS: f64 = 10_000.;
const SECONDS_PER_YEAR: f64 = 60. * 60. * 24. * 365.24;
pub struct InterestBearingConfig {
/// 可以设置利率和授权的授权
pub rate_authority: OptionalNonZeroPubkey,
/// 初始化时间戳,从中进行利息计算
pub initialization_timestamp: UnixTimestamp,
/// 从初始化到上次更新时的平均利率
pub pre_update_average_rate: BasisPoints,
/// 上次更新的时间戳,用于计算累计总额
pub last_update_timestamp: UnixTimestamp,
/// 自上次更新以来的当前利率
pub current_rate: BasisPoints,
}计息扩展的 Type-Length-Value (TLV) 布局
所有 Token-2022 扩展都遵循 Type-Length-Value (TLV) 格式,该格式允许程序轻松读取和跳过存储在账户中的不同扩展数据。
InterestBearingConfig TLV 条目编码为:
- T (
type):0x0A(InterestBearingConfig的类型标识符) - L (
length):0x34(u8,值 = 52 十进制) -
V (
value): 按顺序连接的序列化字段:rate_authority(32 字节)initialization_timestamp(8 字节)pre_update_average_rate(2 字节)last_update_timestamp(8 字节)current_rate(2 字节)
字段 pre_update_average_rate 和 current_rate 不存储为浮点数。相反,它们存储为 基点。
1 基点 = 1/100 (0.01%)
因此,要表示 2.50% 的年利率,你需要在 current_rate 字段中存储整数 250(因为 250 个基点是 250*1/100=2.5%)。要从百分比转换为基点,只需除以 0.01(或等效地,乘以 100)。在本例中,2.5 / 0.01=250。
在 InterestBearingConfig 扩展 TLV 布局中,V 部分是所有扩展字段按顺序连接的序列化值,如我们之前在 Token-2022 文章中所述。
例如,假设扩展包含以下值:
rate_authority:7xKXtg2CW87d9LN6HBUtjQVSiJ9MCrgdGubbyiTZRjrwb(32 字节)initialization_timestamp:1672531200(2023 年 1 月 1 日;8 字节)pre_update_average_rate:500(基点为 5.00%;2 字节)last_update_timestamp:1704067200(2024 年 1 月 1 日;8 字节)current_rate:500(基点为 5.00%;2 字节)
当我们把上面的字段连接成一个连续的字节序列时,TLV 的 V (hex) 部分是:
0x689536DF68C2FB0A61A08DEDC9797145C969328A05D68A2A8C06E15A3AB6BD5200CDB06300000000F4018000926500000000F401完整的 TLV 条目是 T(0x0A) | L(0x34) | V(...),并紧跟在 Mint 账户数据之后。
计息扩展初始化
计息扩展在一个操作中启用和初始化,该操作既保留空间又写入扩展的 TLV。正如我们之前在 Token-2022 文章中讨论的那样,
其他扩展通常需要两个步骤:
- 启用所需的扩展并为扩展保留空间
- 以及一个单独的初始化指令来配置它。
利息计算模型
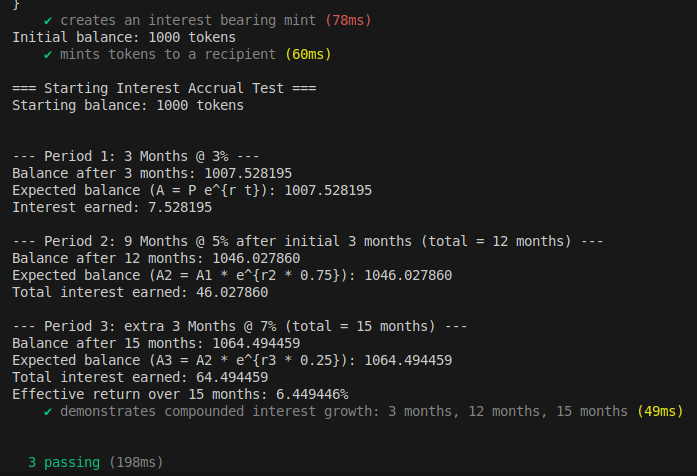
假设你在银行有一个储蓄账户。当你以 3% 的年利率存入 $1,000 时,你的账户对账单不会显示你的银行每天都在 mint 新的美元。相反,银行的系统会计算出如果复利计算,你的余额会增长多少,并在你登录时向你显示更新后的数字。
计息扩展使你的 mint 账户以类似的方式工作。你的链上余额(相当于你银行的余额)永远不会从 $1,000 改变。但是你的钱包(如网上银行应用程序)使用复利公式在六个月后显示显示 **** $1,015 ,或在一年后显示 $1,030。
如果银行稍后将你的利率从 3% 提高到 5%,则未来的利息复利会更快,但你之前的 3% 一年仍然是“锁定”,最终余额将正确反映该时期的 3% 增长率。
计息扩展使用连续复利公式 ( ) 来计算利息,并确保你的应计收益是准确的,无论利率是否变化(我们稍后将详细探讨此公式)。
该公式已硬编码到 Token-2022 程序中,有两种变体:最近一次费率更新的 before 和 after。
before 变体捕获早期利率下的增长(以防授权更新利率),而 after 变体捕获当前利率下的增长。它们共同产生一个连续的、时间加权的复利因子,确保余额在多个利率变化中保持准确。
接下来,让我们通过一个例子展示如何在数学上计算这些运算。
计息扩展如何使用连续复利公式
首先,这里是公式中变量的描述:
- A = 最终金额(本金 + 利息)
- P = 本金(初始金额)
- e = Euler数(大约 2.71828…)
- r = 年利率(以小数表示)
- t = 以年为单位的时间(Token-2022 内部以秒为单位工作)
其中 SECONDS_PER_YEAR = 60 × 60 × 24 × 365.24
以下示例适用于利率未更改的情况:
- 你存入 1000 个 token (P = 1000)
- 利率为 5% (r = 0.05)
- 1 年后 (t = 1)。
- 显示的余额计算为:
让我们也展示一下利率变化时的行为
现在假设利率从 3% 开始,但在前 3 个月后提高到 5%。Token-2022 通过将计算分成几个部分来处理这个问题。
注意:在我们的数学模型中,我们将三个月表示为 0.25 (计算为 3 ÷ 12 = 0.25)
- 更新前增长:
让我们首先计算经过的时间 (t)。
如果我们在公式中用上面计算的 0.25 年代替 t,我们将得到以下结果:
- 更新后增长:
新利率 = 5% ( r₂ = 0.05)
剩余经过时间 = 9 个月,计算为 9/12 (t₂ = 0.75)
从我们目前的计算中,你会注意到利息代表一年的收益。在前三个月(更新前增长期间),用户以 3% 的利率赚取了 7.53 个 token,使其总额达到 1,007.53 个 token。当剩余的九个月(更新后增长期间)利率提高到 5% 时,他们又赚取了 38.5 个 token,最终余额为 1,046.03 个 token。
处理多个利率更新
我们已经了解了这种计算在两个时间段内是如何工作的,但计息扩展可以在 token 的生命周期中多次更新利率。每次更新都确保应计收益与所有过去和未来的利率变化保持一致。
设置新利率时,程序会按如下方式更新 InterestBearingConfig 中的字段:
- 它将
pre_update_average_rate重新计算为所有先前利率的时间加权平均值,包括刚刚被替换的利率。 - 它将
last_update_timestamp向前移动到当前的区块时间。 - 它将
current_rate设置为新的利率值(例如,7% 为700个基点)。
在数学上,我们可以使用下面的公式重新计算所有先前利率的新的时间加权平均值(pre_update_average_rate):
其中:
- r₁ →
pre_update_average_rate(先前的平均利率) - t₁ →
last_update_timestamp - initialization_timestamp(所有先前利率下的经过时间) - r₂ →
current_rate(更新之前的最新利率) - t₂ →
current_timestamp - last_update_timestamp(当前利率下的经过时间)
时间加权平均值的示例计算
假设我们从以下内容开始:
initialization_timestamp = 0pre_update_average_rate = 300(3%)last_update_timestamp = 7889184秒(~3 个月。InterestBearingConfig扩展存储绝对 Unix 时间戳,但在本例中,我们使用 3 个月的经过时间(以秒为单位)来说明利息增长,因为利息仅取决于时间的流逝,而不取决于特定的时间戳值)current_rate = 500(5%)current_timestamp = 31556736(≈ 1 年)new_rate = 700(7%)
然后:
更新后:
pre_update_average_rate = 450(4.50%)last_update_timestamp = 31556736current_rate = 700(7%)
公式的代码说明
更新前增长期和更新后增长期****在扩展的源代码中实现为 pre_update_exp 和 post_update_exp 函数。定义这两个函数的部分如下所示。
pre_update_exp 和 post_update_exp 函数直接实现连续复利公式 (),特别是两个不同时间段(最近一次利率更新之前和之后)的利息增长因子 ()。
-
pre_update_exp计算 token 初始化和上次利率更新之间的时间内的复利增长。-
它将该期间的平均利率(
pre_update_average_rate)乘以以秒为单位的经过时间。 -
它将分子除以:
-
一年中秒数(
SECONDS_PER_YEAR),将时间从秒转换为年,以及 -
常数
ONE_IN_BASIS_POINTS(等于 10,000),将利率从基点转换为十进制。 -
最后,它计算
exponent.exp(),它是该期间的连续增长因子(Euler数提高到指数的幂)。这在数学上表示为 。
-
post_update_exp执行相同的计算,但使用当前利率(current_rate)和自上次更新以来经过的时间(post_update_timespan)。
以下是 Token-2022 代码库中的函数 pre_update_exp 和 post_update_exp:
pub struct InterestBearingConfig {
/// 可以设置利率和授权的授权
pub rate_authority: OptionalNonZeroPubkey,
/// 初始化时间戳,从中进行利息计算
pub initialization_timestamp: UnixTimestamp,
/// 从初始化到上次更新时的平均利率
pub pre_update_average_rate: BasisPoints,
/// 上次更新的时间戳,用于计算累计总额
pub last_update_timestamp: UnixTimestamp,
/// 自上次更新以来的当前利率
pub current_rate: BasisPoints,
}
fn pre_update_exp(&self) -> Option<f64> {
let numerator = (i16::from(self.pre_update_average_rate) as i128)
.checked_mul(self.pre_update_timespan()? as i128)? as f64;
let exponent = numerator / SECONDS_PER_YEAR / ONE_IN_BASIS_POINTS;
Some(exponent.exp())
}
fn post_update_exp(&self, unix_timestamp: i64) -> Option<f64> {
let numerator = (i16::from(self.current_rate) as i128)
.checked_mul(self.post_update_timespan(unix_timestamp)? as i128)? as f64;
let exponent = numerator / SECONDS_PER_YEAR / ONE_IN_BASIS_POINTS;
Some(exponent.exp())
}
fn post_update_timespan(&self, unix_timestamp: i64) -> Option<i64> {
unix_timestamp.checked_sub(self.last_update_timestamp.into())
}
为了计算精确的复利——无论利率是否已更改——计息扩展使用 total_scale 函数。
它乘以 pre_update_exp 和 post_update_exp 的结果,它们分别表示上次利率更新之前和之后的增长因子。
该乘积给出两个时间段的总指数增长因子。
最后,total_scale 函数将结果除以 10^decimals 以将该值缩放到 token 的标准精度。例如,SOL token 有 9 位小数,因此 pre_update_exp 和 post_update_exp 的结果将除以 10^9。
total_scale 的结果值是应用于链上余额的缩放因子,以准确显示连续复利。
fn total_scale(&self, decimals: u8, unix_timestamp: i64) -> Option<f64> {
Some(
self.pre_update_exp()? * self.post_update_exp(unix_timestamp)?
/ 10_f64.powi(decimals as i32),
)
}换句话说,计息扩展中每次利息计算的结果值都是本金和 total_scale 的乘积。
计息扩展如何在内部应用公式
以下是使此计算在内部成为可能的三种重要字段:
pre_update_average_rate: 存储累积增长因子(公式中的指数),直到上次利率更新。在我们的示例中,3 个月后,这将捕获0.03 × 0.25 = 0.0075。last_update_timestamp: 标记上次利率更新发生的准确时间。在示例中,这是第 3 个月的时间戳。current_rate: 当前生效的利率。在示例中,这在 3 个月后从0.03切换到0.05。
当钱包或程序查询余额时,计息扩展会重建公式:
这相当于我们在前面提到的 total_scale 函数中的内容:
fn total_scale(&self, decimals: u8, unix_timestamp: i64) -> Option<f64> {
Some(
self.pre_update_exp()? * self.post_update_exp(unix_timestamp)?
/ 10_f64.powi(decimals as i32),
)
}UI 显示余额转换功能
计息扩展公开了 两个函数,钱包和应用程序使用这些函数来一致地显示链下余额:
- 将原始金额转换为 UI 金额(
amount_to_ui_amount)的函数,该函数首先计算应计利息(token 金额 * 总比例),然后使用给定的十进制精度将结果格式化为字符串,并删除不必要的零。
/// 使用给定的十进制字段将原始金额转换为其 UI 表示形式。删除多余的零或不需要的小数点。
pub fn amount_to_ui_amount(
&self,
amount: u64,
decimals: u8,
unix_timestamp: i64,
) -> Option<String> {
let scaled_amount_with_interest =
(amount as f64) * self.total_scale(decimals, unix_timestamp)?;
let ui_amount = format!("{scaled_amount_with_interest:.*}", decimals as usize);
Some(trim_ui_amount_string(ui_amount, decimals))
}- 以及
try_ui_amount_into_amount,它将 UI 余额(包括计算出的利息的余额)转换回内部使用的原始金额(不含利息)。以下是计息源代码中的原始实现。
/// 尝试使用给定的十进制字段将 token 金额的 UI 表示形式转换为其原始金额
pub fn try_ui_amount_into_amount(
&self,
ui_amount: &str,
decimals: u8,
unix_timestamp: i64,
) -> Result<u64, ProgramError> {
let scaled_amount = ui_amount
.parse::<f64>()
.map_err(|_| ProgramError::InvalidArgument)?;
let amount = scaled_amount
/ self
.total_scale(decimals, unix_timestamp)
.ok_or(ProgramError::InvalidArgument)?;
if amount > (u64::MAX as f64) || amount < (u64::MIN as f64) || amount.is_nan() {
Err(ProgramError::InvalidArgument)
} else {
// 这很重要,如果你更早地进行舍入,你将得到错误的“inf”
// 答案
Ok(amount.round() as u64)
}
}上述函数(amount_to_ui_amount 和 try_ui_amount_into_amount)不在链上执行。它们是在 Rust SDK 中实现的客户端辅助函数(也在 TypeScript SDK 中镜像)。
钱包兼容性
Token-2022 扩展尚未获得 Solana 生态系统中钱包的广泛支持。由于计息 token 的链上余额永远不会改变,因此钱包必须检测 mint 上的计息扩展,并在显示用户余额之前应用复利公式。如果没有此逻辑,钱包将始终显示原始本金金额,而忽略应计增长。
这种差异意味着两个钱包可以显示相同账户的不同结果:一个仅显示链上存储的固定金额,另一个显示从扩展字段导出的连续复利余额。在钱包更新其账户渲染以包括 Token-2022 扩展之前,依赖于计息 token 的应用程序通常需要自行计算和显示余额。
结论
在本文中,我们讨论了计息 token 扩展的工作原理,以及它如何引入一种直接在 token mint 级别表示收益的方法,而无需链上余额更新或定期分配交易。
我们还讨论了所有应计费用如何通过链下确定性公式发生,从而使系统高效,同时仍为用户提供余额增长的体验。
显示背后的数学原理确保应计利息正确复利,并且钱包集成可以依赖所提供的函数来保持余额一致。
跨钱包和浏览器的支持仍然有限,因此目前采用此功能的应用程序必须承担正确显示余额的责任。
本文是 Solana 上的教程系列 的一部分。
- 原文链接: rareskills.io/post/token...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 学分: 30
- 分类: Solana
- 标签: Token-2022 interest-bearing extension 利息计算 连续复利 链下计算 Solana
