为富状态的比特币脚本探索 Lamport 和 Winternitz 签名

作者：Nicolas Vescovo

来源： https://www.rootstocklabs.com/blog/exploring-lamport-and-winternitz-signatures-for-stateful-bitcoin-scripts/

“BitVM” 这一框架的设计目的是将任意链外计算的乐观主义验证（optimistic verification）带给比特币网络，从而允许更加复杂的操作，比如 “zk rollup” 和侧链桥。BitVM 通过引入支持乐观主义验证的机制，增强了比特币的灵活。“BitVMX” 则使用不同的技术，让部分操作能够更快、更高效地检查，取得了更好的成果。在这一语境下，“乐观主义验证” 表示基于一种假设的验证方法 —— 假设 操作都是有效的，除非能证明不是。

为了保证这样的系统的安全性，BitVM 和 BitVMX 使用 Lamport 签名和 Winternitz 签名。这些密码学方法是确保整个过程具有 “富状态性（statefulness）” 的关键。通过使用这些签名方案，BitVM 和 BitVMX 提供了强大的安全性，可以抵御多种攻击并保证所有操作都得到了正确执行。

本文解释了 “Lamport 签名” 和 “Winternitz 签名” 分别是什么样的、后者如何延申了前者的概念，以及它们如何用在 BitVM 中。我们也将解释，这些签名如何在 BitVM 和 BitVMX 中带来富状态性、确保特定的变量一旦被设定，在后续的脚本中就无法再修改和复用。

理解 Lamport 签名和 Winternitz 签名

一种电子签名方案就是一种用来验证电子消息（或者说文档）的真实性和完整性的数学方案。简单来说：

• Lamport 签名使用了 一次性的电子承诺（基本上基于哈希函数）来提供不可伪造的签名。
• Winternitz 签名则利用 一种单向函数的多轮迭代（通常会形成链条）来实现密码学安全性。

Lamport 签名：由 Leslie Lamport 在 1970 年代晚期提出，是一种基于哈希函数的电子签名方案。它利用密码学哈希函数的单向特性来获得安全性。Lamport 签名因其简洁性以及抵御量子计算攻击的能力而闻名。它的模式是预先生成大量的密钥对，然后用它来签名。不过，其巨大的签名体积，也可能会限制其应用。

Winternitz 签名：由 Ralph Merkle 和 Robert Winternitz 分别独立提出，是另一种基于哈希函数的电子签名。它提供了跟 Lamport 签名相似的安全性，且更加高效。相比 Lamport 签名，Winternitz 签名利用了一种链条结构，降低了签名的大小，这使它更加实用。通过允许用户调整 Winternitz 参数，这些签名可以在计算速度和签名体积之间取得平衡，实质上，是将 Lamport 签名方案一般化了。

Lamport 签名：形式化视角

在本章中，我们提供了对 Lamport 签名如何生成、使用和验证的分步骤解释。我们探索了密钥生成过程、消息签名和签名验证的技术方面。最后，我们讨论了与之有关的安全性考虑和弱点。

密钥生成

为需要签名的消息中的每一个比特 $i$ 生成两串随机的字符串（比特序列），分别记为 $S{i,0}$ 和 $S{i,1}$ 。如果消息的长度是 $n$ 比特，那么 $i$ 的取值范围是从 $0$ 到 $n-1$ 。

私钥就是由这些随机字符串对 $(S{i,0}, S{i,1})$ 组成的（其中 $i=0,1,…,n-1$）。

对于私钥中的每一对字符串 $(S{i,0}, S{i,1})$ ，计算这些字符串的哈希值并保持配对：$(H(S{i,0}), H(S{i,1}))$ 。

公钥则是由这些哈希值对 $(H(S{i,0}), H(S{i,1}))$ 组成的（其中 $i=0,1,…,n-1$）。

签名消息

将待签名的消息 $m$ 转化为二进制形式，即 $m = m_0 m1 … m{n-1}$ ，每一个 $m_i$ 都是一个比特（其值为 0 或 1 ）。

对于消息的每一个比特 $mi$ ，在签名中包含对应的私钥 $S{i,m_i}$ 。

最终，签名就是一个有 $n$ 个元素的序列：$(S_{0, m0}, S{1, m1},...,S{n-1, m_{n-1}})$。

验证一个签名

给定一条消息 $m$ 及其签名 $(S_{0, m0}, S{1, m1},...,S{n-1, m_{n-1}})$ 。

将消息 $m$ 转化为二进制形式：$m = m_0 m1 … m{n-1}$ 。

对于每一个比特 $mi$ ，计算签名中对应元素的哈希值：$H(S{i,m_i})$ 。

验证计算出来的每一个哈希值 $H(S_{i,mi})$ 都跟公钥中的对应元素（$H(S{i,0})$ 或 $H(S_{i,1})$）相匹配。

安全考虑

• 一次性使用：仅在每一对密钥只用来签名一条消息时，Lamport 签名方案才是安全的。使用同一对密钥来签名多条消息会揭晓部分私钥，从而牺牲安全性。
• 哈希函数：Lamport 签名方案的安全性依赖于所用的密码学哈希函数的强度 —— 它应该能抵抗原像攻击、第二原像攻击以及碰撞攻击。

为什么它们叫 “一次性签名”？

Lamport 签名方案被称作 “一次性签名”，因为在这种方案中，一旦同一把公钥用来签名多于一条消息，其安全性就会急剧下降。其中的道理在于，每多签名一条消息，就会多揭晓一些关于私钥的信息，从而让攻击者更容易伪造签名。

在观察到一个签名之后，攻击者就知道了公钥中的每一对哈希值中的一个的原像。然而，有了两个签名，攻击者就能知道其中一半哈希值对的两个原像，以及另一半哈希值对的一个原像。有了三个签名，攻击者就能知道其中四分之三的哈希值对的两个原像；以此类推。这种逐步的曝光，意味着同一个公钥每多签一个名，其安全性实质上都会减半。

（译者注：作者在上一段的推理中使用了消息的比特随机分布的假设。）

举个例子，如果一个公钥被设计成对第二原像攻击提供 256 比特的安全性以及对碰撞攻击提供 128 比特的安全性，在它签名三次之后，实用的攻击就有可能发动。在它签名四次之后，找出 消息-签名 的配对就变得非常简单了。因为攻击者可以使用已知的哈希值（及其原像）来为自己选定的消息构造新的有效签名，漏洞由此产生；在消息有一些灵活性的语境中尤其如此。

在使用超过一次时 Lamport 签名的漏洞

Lamport 签名在同一公钥重复签名时的主要漏洞在于，攻击者能够利用从以往观察到的签名中获得的信息，为任意消息伪造签名。假设一个攻击者能够知晓使用同一个公钥为多条消息生成的签名。这时候，TA 就能将已知的签名拼凑在一起，构造出新的有效签名。

比如说，考虑一个消息长度为 16 比特的情形：

签过名的消息有：$m_1 = 0001111101110001$ 以及 $m_2 = 0111110000111111$ 。攻击者就能为一条新消息 $m^ = 0101111000110101$ 伪造签名，只需要将对上述两条消息的签名中的对应部分拼凑起来。但凡是使用从 $m_1$ 和 $m_2$ 的对应位置的比特构造出的 $m^$ ，就都能伪造出有效的签名 —— 只需要对应于这些比特的值的哈希值的原像，就能构造出签名。

如果消息在签名之前哈希过（也即签名的不是消息本身，而是消息的哈希值），那么攻击就要变得更加复杂，但依然是可行的。攻击者必须找出一条消息 $m^*$ ，其哈希值与以往签过名的消息的哈希值有足够多相同的部分。每多一条可以观察到的签名，都可以减少攻击所需的哈希函数求值的次数，也就是让伪造变得更加容易。

本质上，在使用 Lamport 签名方案时，为了保持安全性，每个公钥都只应使用一次。为多条消息的签名重复使用一个公钥，将允许攻击者获得足够多的信息来伪造新的签名，最终打破这种密码系统的完整性。

Winternitz 签名：理论视角

如我们已经介绍过的，Winternitz 一次性签名（WOTS）是 Lamport 签名的一种强化，极大地缩小了签名和公钥的体积。但天下可没有免费的午餐。这种提升的代价是，生成和验证签名都要更花功夫。在本章中，我们会提供一种形式化的定义，并解释 Winternitz 签名是如何工作的。

参数与启动

• $W$：Winternitz 参数，一个正整数，决定一次能处理的比特数量。
• $n$：哈希输出的长度（以比特计）。
• $l$：消息摘要的分段数量，计算方式是 $l = \lceil n/W \rceil$ 。这里的 $\lceil \rceil$ 意味着取大于或等于给定数字的最小整数 。
• $l’$：校验和的长度，计算方式是 $l' = \lceil (log_2(l * (2^W - 1))) / W \rceil$
• $L$：签名的总长度，$L = l + l’$ 。

密钥生成

生成 $L$ 个长度为 $n$ 的随机比特串 $S_i$ ，其中 $i=0,1,…,L-1$ 。

私钥就是由这些随机比特串组成的：$S = (S_0, S1, …, S{L-1})$ 。

对于每一个私钥碎片 $S_i$ ，连续应用哈希函数 $2^W$ 次：$P_i = H^{2^W}(S_i)$ 。

公钥就是用这些哈希结果组成的：$P = (P_0, P1, …, P{L-1})$

签名消息

将待签名的消息 $m$ 分割为长为 $W$ 比特的 $l$ 个碎片：$m = (m_0, m1, …, m{l-1})$ 。

计算校验和 $C$ ：$C = \sum_{i=0}^{l-1} (2^W - 1 - m_i)$ 。

将校验和 $C$ 转化为长为 $W$ 比特的 $l’$ 个碎片：$C = (c_0, c1, …, c{l'-1})$ 。一般来说，会把第一个元素当成校验和：$C = (c_0)$ 。

对于摘要的每一个碎片 $m_i$ 以及校验和 $c_i$ ，通过哈希对应的私钥碎片 $m_i$ 次来生成签名 $\sigma_i$ ：$\sigma_i = H^{m_i}(S_i)$ ，其中 $i=0,1,…,l-1$ 。

类似的，对于校验和的部分：$\sigma_{l+j} = H^{cj}(S{l+j})$ ，其中 $j=0,1,…,l'-1$ 。

完整的签名就是这些碎片的拼接：$\sigma = (\sigma_0, \sigma1, …, \sigma{L-1})$ 。

验证签名

给定消息 $m$ 及其签名 $\sigma = (\sigma_0, \sigma1, …, \sigma{L-1})$ 。

将消息 $m$ 分割成 $l$ 份：$m = (m_0, m1, …, m{l-1})$ 。

计算校验和 $C$ 并将它分割成 $l’$ 份：$C = (c_0, c1, …, c{l'-1})$ 。

对于每一个签名碎片 $\sigma_i$ ，应用哈希函数 $2^W - 1 - m_i$ 次，期待它能推导出公钥碎片：

$P_i: P_i = H^{2^W - 1 - m_i}(\sigma_i), i=0,1,…,l-1$

类似地，对于校验和的部分：

$P_{l+j} = H^{2^W - 1 - cj}(\sigma{l+j}), j=0,1,…,l'-1$

如果派生出来的公钥 $(P_0, P1, …, P{L-1})$ 与公钥 $P = (P_0, P1, …, P{L-1})$ 相匹配，则说明这是个有效的签名。

安全考虑

• 参数挑选：$W$ 的选择会影响签名体积与计算效率的取舍。更大的 $W$ 值会降低签名的体积，但会提高签名和验证的计算负担。
• 一次性使用：与 Lamport 签名一样，Winternitz 签名也是一次性使用的。在多条消息的签名中重复使用同一对密钥，会因为揭晓关于私钥的信息而牺牲安全性。

下图演示了当 $W = 2$ ，$l = 5$ 时，Winternitz 链条的序列（从私钥派生公钥）。每一个箭头都表示一次哈希求职。

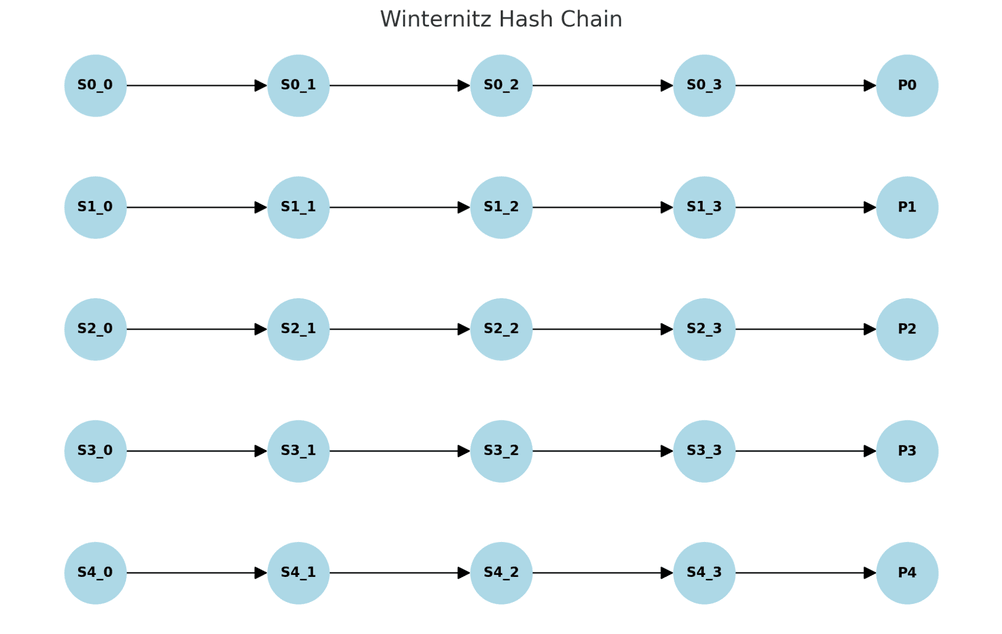
为什么校验和是必要的？

从技术角度看，Winternitz 签名方案中的校验和，对于保持安全性和保证签名过程的完整性，都是必要的。

Winternitz 签名方案的模式是将消息分割成碎片，然后根据各碎片的值将对应的私钥碎片哈希一定的次数。然而，这个过程就带来了一个漏洞：只要攻击者知道一个签名（它由各哈希链条上的某个值组成），就可以使用哈希链条上的后续元素来构造有效的签名。这是因为，只要揭晓了哈希链条上的一个成员，攻击者就可以计算出所有后续的哈希值（它们本身就是同一私钥碎片对某个值的签名），从而打破签名的完整性。

为了消除这种风险，检验和就是关键了。它保证了，对消息的任何改动，都会让校验和也发生对应的、一致的改动，而这种计算，在没有私钥的情况下是计算上不可行的。因为，想要使用一些哈希链条上的后续的值，将需要知道签名校验和的哈希链条上比较靠前的值（在没有私钥的情况下，这是不可能做到的）。校验和是一个额外的验证层，让没有原像攻击能力的攻击者无法在不知道私钥的情况下为另一条消息生成一个有效的签名。

（译者注：此处的推理是，由于哈希链条是单向的，所以，在不考虑校验和的情况下，知晓一条 WOTS 签名只允许攻击者为数值更大的各个 $mi$ 伪造签名，也即使用哈希链条上更靠后的值。然而，在使用前述校验和 $C = \sum{i=0}^{l-1} (2^W - 1 - m_i)$ 的情况下，更大的 $m_i$ 将带来更小的 $C$，签名这样的 $C$ 将要求使用私钥哈希链条上更为靠前的值，想要从已知的签名中推导出它意味着逆转哈希运算，这是计算上不可行的。因此，如无私钥，就无法制作出签名。）

此外，校验和也保证了签名过程的完整性。它是一个最终的检查，验证在签名过程中没有遗漏或替换某个比特。这保证了整条消息都被考虑到了、在签名中有了正确的表示。

此外，校验和还验证了签名的整体完整性。也就是说，应用了正确的哈希迭代次数，从而保证签名既准确又安全。

没有校验和，这种方案是很容易被攻击的。攻击者可以很容易替换掉消息碎片，并在没有私钥的情况下创建出有效的签名。缺乏校验和也可能导致不完整验证，让替换或截短的消息也被当成是签过名的。

BitVM 和 BitVMX：Lamport 签名和 Winternitz 签名闪耀的地方

我们已经提到，BitVM 和 BitVMX 是为了将任意链外计算的乐观验证带给比特币网络而设计的框架。两者都能使用 Lamport 签名或 Winternitz 签名来创建健壮的数据承诺。在这个语境下，一个承诺是特定的一段数据在某个时间点已经存在、被安全记录、且签过名的密码学保证。这些承诺可以在未来验证者的挑战中被引用。这些签名的使用，保证了每一个承诺都是可以验证并且抗篡改的。

如果验证者同意操作者，那就不需要做什么，操作就会正常处理；但如果验证者不同意操作者，因为双方都曾公开签名这些承诺，所以协议允许双方使用对方的信息来证明对方尝试欺诈或正在执行错误的操作。

BitVM 带来的一项关键创新是能够跨越多笔交易而保持和引用状态。这是通过使用一次性签名来承诺每一步骤时刻的状态来实现的。通过利用 Lamport 签名，BitVM 保证了每一次状态转换都得到了安全的承诺，并且可以在后续操作中可靠地引用。

结论

Lamport 签名和 Winternitz 签名有一系列好的属性，使它们适合在 BitVM 和 BitVMX 中使用。它们集成到这些协议中，极大地加强了比特币的脚本编程能力，带来了高效且安全的富状态操作。它们在数据承诺中的用法，保证了网络可以处理更加复杂的交易但保持安全性和性能。这些密码学技术，是比特币未来的关键，因为它们为更加高级和安全的去中心化应用（比如信任最小化的侧链桥、乐观验证的零知识证据）铺平了道路。

（完）

• 本文转载自： btcstudy.org/2026/01/27/... , 如有侵权请联系管理员删除。