Slither漏洞扫描框架使用(初级篇)
07.Slither中间语言数据结构分析-node对象
- 小驹
- 发布于 2023-06-30 10:52
- 阅读 4491
1.理解irs与irs_ssa的区别。 2.理解实现ssa时的支配边界的定义。 3.理解Node对象常用的方法。
本文中关于支配边界的部分参考互联网中的内容。
1. irs与irs_ssa的区别
Static Single Assignment (SSA) 是一种通常用于编译和静态分析的表示。它要求每个变量只分配一次并且在使用之前就进行定义,具体可以参考链接。
这两个属性是一个列表,分别对应着当前node的中间表示,和ssa方式的中间表示。
如下面的函数中
function func_A (uint user_input) public {
uint a;
a = user_input;
func_B(a);
}会生成下面的4个node
0 = {Node} ENTRY_POINT 1 = {Node} NEW VARIABLE a 2 = {Node} EXPRESSION a = user_input 3 = {Node} EXPRESSION func_B(a)
对于index为2的node:a = user_input,这个node中只有一条ir,该ir在使用ssa与不使用ssa的中间表示中有所不同:
- 不使用ssa的中间表示时,该ir直接为a(uint256) := user_input(uint256)
- 使用ssa的中间表示时,该ir为a_1(uint256) := user_input_1(uint256)
2. node对象主要成员变量和函数
2.1 取得node对象的slithIR表达式
有两个函数可以得到
- irs()
- irs_ssa()
分别返回当前结点的slithIR表达式和SSA表示的slithIR表达式。
2.2 子/父节点列表
通过sons/fathers的属性可以获得当前 Node对象的子/父节点列表。
该属性直接返回node的子node列表(或者父node节点)。通常应用在遍历Node时。
如下面的函数中
function func_A (uint user_input) public {
uint a;
a = user_input;
func_B(a);
}会生成下面的4个node
0 = {Node} ENTRY_POINT 1 = {Node} NEW VARIABLE a 2 = {Node} EXPRESSION a = user_input 3 = {Node} EXPRESSION func_B(a)
0号Node对象的sons是一个列表,该列表中只有一个Node(对应着{Node} NEW VARIABLE a)
2.3 Node类型
使用type属性可以得到当前Node的类型,这些类型表明这个Node是个入口点节点还是表达式节点还是IF节点还是变量节点。常用类型有NodeType.ENTRYPOINT、NodeType.ENDIF、NodeType.EXPRESSION。
Node节点到底有多少种类型呢?从代码中看,有下面的类型
ENTRYPOINT = 0x0 # no expression
Node with expression
EXPRESSION = 0x10 # normal case RETURN = 0x11 # RETURN may contain an expression IF = 0x12 VARIABLE = 0x13 # Declaration of variable ASSEMBLY = 0x14 IFLOOP = 0x15
Merging nodes
Can have phi IR operation
ENDIF = 0x50 # ENDIF node source mapping points to the if/else body STARTLOOP = 0x51 # STARTLOOP node source mapping points to the entire loop body ENDLOOP = 0x52 # ENDLOOP node source mapping points to the entire loop body
Below the nodes have no expression
But are used to expression CFG structure
Absorbing node
THROW = 0x20
Loop related nodes
BREAK = 0x31 CONTINUE = 0x32
Only modifier node
PLACEHOLDER = 0x40
TRY = 0x41 CATCH = 0x42
Node not related to the CFG
Use for state variable declaration
OTHER_ENTRYPOINT = 0x60
2.4 取得Node节点的变量列表
这类的函数有local_variables_read/local_variables_written/state_variables_read/state_variables_written。
该Node节点读取或者写入的变量列表。是个list结构,列表的每个元素为variable类型。
| 属性 | 解释 |
|---|---|
| local_variables_read | 当前节点读取过的变量的列表 |
| local_variables_written | 当前节点写入过的变量的列表 |
| state_variables_read | 当前节点读取过的状态变量的列表 |
| state_variables_written | 当前节点写入过的状态变量的列表 |
🎉 扩展:Function对象也有这4个属性保存对应的变量列表
2.5 取得node中声明的变量对象vriable_declaration
如果当前node的类型为VARIABLE,表明该Node中会声明变量,那么如何取得声明的变量对象呢?使用node.variable_declaration属性。
如下面代码中的索引为1的Node中,Node的类型就为VARIABLE = 0x13 ,表示该Node声明变量的,node.variable_declaration就会对应着a VARIABLE对象。
对于其他的几个Node,variable_declaration都对应着None.
function func_A (uint user_input) public {
uint a;
a = user_input;
func_B(a);
}会生成下面的4个node
0 = {Node} ENTRY_POINT
1 = {Node} NEW VARIABLE a
2 = {Node} EXPRESSION a = user_input
3 = {Node} EXPRESSION func_B(a)
2.6 取得node对象的支配边界相关的内容
取得支配边界相关数据有如下的的函数
- dominance_exploration_ordered
- dominance_frontier
- dominance_frontier(doms)
- dominator_successors
- dominators
- dominators(doms)
对支配边界的理解,要先理解支配的定义,再理解支配树的定义,再理解到支配边界。
💡 按照 支配→支配树→支配边界 的方式来理解
支配边界。支配边界直观理解就是当前结点所能支配的边界(并不包括该边界)。
Y 是 X的支配边界,当且仅当 X支配 Y的一个前驱结点(CFG)同时 X 并不严格支配 Y。
涉及到编译原理的知识,可以参考:https://blog.dyf.ink/blog/ssa1
简单来说,先看支配的定义,再看支配树的定义,再看支配边界的定义进行直观的理解。
2.6.1 取得支配边界的目的
支配边界的意义在于计算SSA时确定 Φ函数 插入位置
支配边界dominance_frontier就表示了当前Node刚好能力所不能及的地方。
2.6.2 对支配边界相关概念的理解
什么是支配
如果每一条从流图的入口结点到结点 n 的路径
都经过结点 d, 我们就说 d 支配(dominate)n,记为 d dom n。
下边的流程图为例:
https://imgconvert.csdnimg.cn/aHR0cDovL2ltZy5ibG9nLmNzZG4ubmV0LzIwMTYwODA5MTYyODM0Njcy
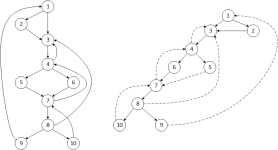 上面的流程图的入口结点是 1 ,入口结点支配所有结点(这个结论对所有的流图都成立)。结点 2 只能支配它自己,因为控制流可以通过 1 -> 3 开头的路径到达所有其他结点,所以结点 3 支配除 1、2 之外的所有其他结点。
上面的流程图的入口结点是 1 ,入口结点支配所有结点(这个结论对所有的流图都成立)。结点 2 只能支配它自己,因为控制流可以通过 1 -> 3 开头的路径到达所有其他结点,所以结点 3 支配除 1、2 之外的所有其他结点。
1支配所有结点。
2支配2结点。
3支配3,4,5,6,7,8,9,10
4支配4,5,6,7结点。
5只能支配自己。因为结点5管不到1,2,3,4,6,而7,8,9,10又可以绕过结点5到达,5只能支配自己。
6支配6,7结点。
7支配7,8,10结点
8支配8,10结点。
9只支配自己。Dominator Tree——支配树
一种树型结构。边表示父结点支配子结点,与CFG的边可完全不是一个意思。
The dominator relationship forms a tree. Edge from parent to child = parent dominates child.Note: edges are not same as CFG edges!
支配树(dominator tree)用来表示支配信息,在树中,入口结点,并且每个结点只支配它在树中的后代结点。
一种支配树的示例如下
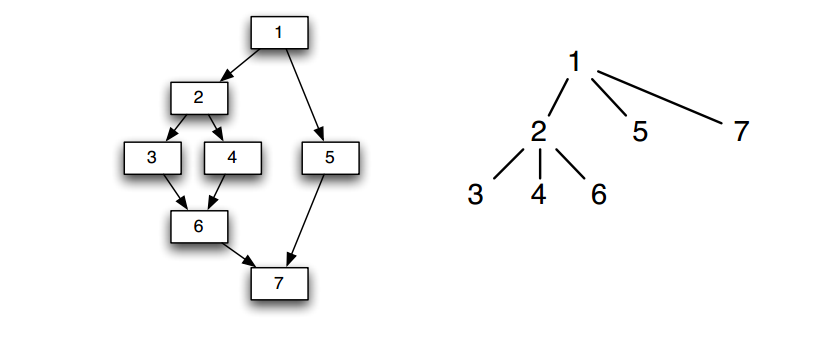
在这个支配树中
1支配2,3,4,5,6,7
2支配3,4,6,7
3支配6,7
4支配6,7
5支配7支配边界(Dominance Frontier)
在构造 SSA 过程中,还有另外一个概念很重要,就是支配边界(dominance frontier)。支配边界直观理解就是当前结点所能支配的边界(并不包括该边界)。
Y is in the dominance frontier of X iff “there exists a path from X to Exit through Y such that Y is the first node not strictly dominated by X”
上面的描述有点绕口,上面的描述也有另一种等价描述“Y 是 X 的支配边界,当且仅当 **X** 支配 **Y** 的一个前驱结点(***CFG***)同时 X 并不严格支配 **Y**”。
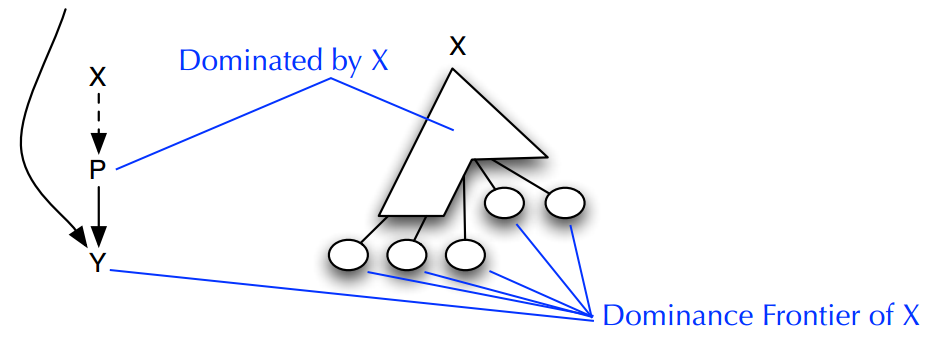
上面的图示直观的表示了支配边界的概念。下面的图给出了一个示例,给出了图中的支配结点以及支配边界关系。
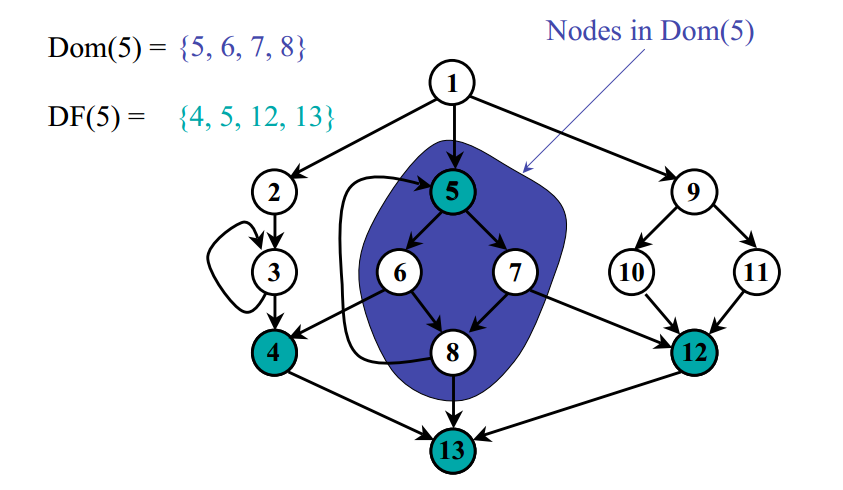
上图中结点 5 支配边界是 4、5、12、13,也就是结点 5 “刚好能力所不能及的地方”。
🎉 上图中 结点5支配5,6,7,8 结点5的支配边界为4,5,12,13
