标题 :Aweave 第 17 版白皮书解读(四):存储完整数据副本才是王道
- PermaDAO
- 发布于 2024-04-01 14:46
- 阅读 3265
在解读(三)文中,我们通过数学推导对 SPoRes 的可行性进行了论证。文中的 Bob 与 Alice 一起参与了这场证明游戏。那在 Arweave 挖矿中,协议部署了这个 SPoRes 游戏的修改版本。在挖矿过程中,协议充当了 Bob 的角色,而网络中的所有矿工共同扮演 Alice 的角色。
 作者: Gerry Wang
作者: Gerry Wang
来源:Arweave Oasis
在解读(三)文中,我们通过数学推导对 #SPoRes 的可行性进行了论证。文中的 Bob 与 Alice 一起参与了这场证明游戏。那在 #Arweave 挖矿中,协议部署了这个 SPoRes 游戏的修改版本。在挖矿过程中,协议充当了 Bob 的角色,而网络中的所有矿工共同扮演 Alice 的角色。SPoRes 游戏的每个有效证明都用于创建 Arweave 的下一个区块。具体说来,Arweave 区块的产生与以下参数相关:
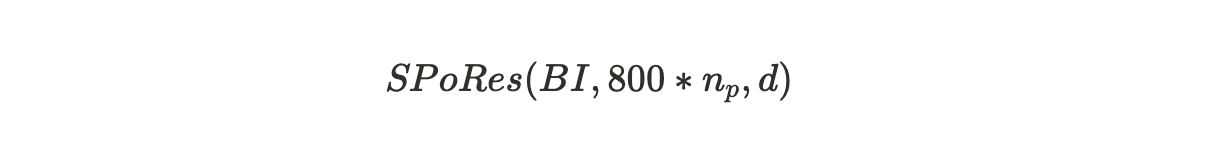
其中:
BI = Arweave 网络的区块索引 Block Index;
800*n_p = 每个检查点每个分区最多解锁 800 个哈希次数,n_p 是矿工存储的大小为 3.6 TB 的分区的数量,两者相乘是该矿工每秒最大可以尝试的哈希运算次数。
d = 网络的难度。
一个成功有效的证明是那些大于难度值的证明,而这个难度值会随时间变化而被调整,以确保平均每 120 秒挖出一个区块。如果区块 i 与区块(i+10)之间的时间差为 t ,那么从旧难度 di 到新难度 d{i+10} 的调整如下计算:
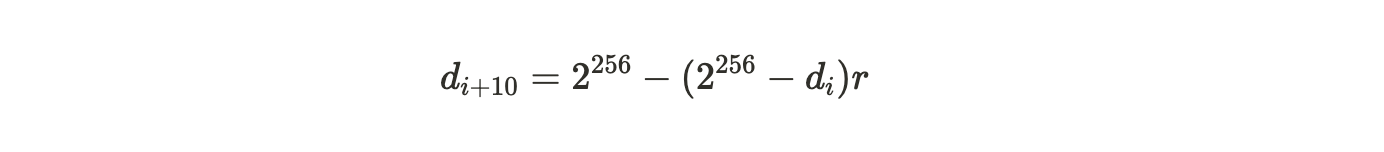
其中:
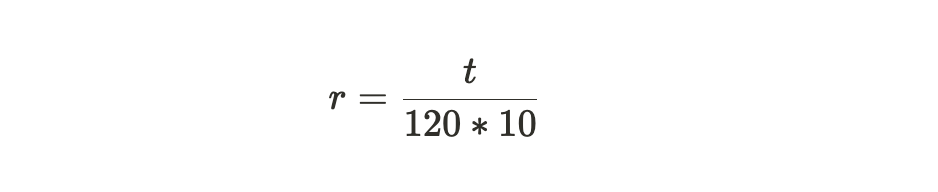
公式注解:从上面两个公式中可以看出, 网络难度的调整主要靠参数 r,而 r 意味着实际的区块产生所需要的时间相对于系统期望的 120 秒一个区块的标准时间的偏移参数。
新计算的难度决定了基于每个生成的 SPoA 证明,挖掘区块成功的概率,具体如下:
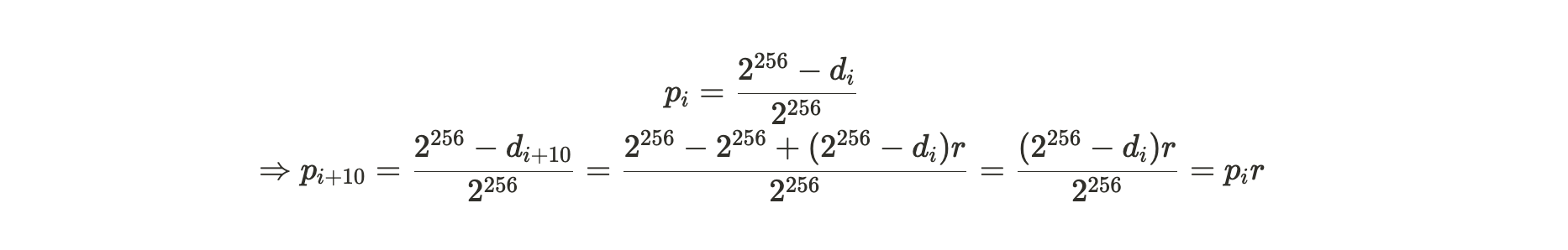
公式注解:经过以上推导可以得到新难度下的挖掘成功概率是旧难度下成功概率乘以参数 r。
同样,VDF 的难度也会重新计算,目的是为了保持检查点周期在时间上能够每秒发生一次。
完整副本的激励机制
Arweave 通过 SPoRes 机制来生成每个区块是基于这样一个假设:
在激励下,无论是个体矿工还是群体合作矿工,都会以维护完整数据副本作为挖矿的最佳策略来执行。
在先前介绍的 SPoRes 游戏中,存储数据集的同一部分的两个副本所释放的 SPoA 哈希数量与存储整个数据集的完整副本是相同的,这就给矿工留下了投机行为的可能。于是 Arweave 在实际部署这套机制的时候,对其作了一些修改,协议通过将每秒解锁的 SPoA 挑战数量分成两部分
- 一部分在矿工存储的分区中指定一个分区来释放一定数量的 SPoA 挑战;
- 另一部分则是在 Arweave 所有数据分区中随机指定一个分区来释放 SPoA 挑战,如果矿工没有存储这个分区的副本,则会失去这一部分的挑战数量。
这里也许你会觉得有些疑惑,SPoA 与 SPoRes 之间究竟是什么关系。共识机制是 SPoRes,为什么释放的却是 SPoA 的挑战?其实它们之间是一种从属的关系。SPoRes 是这个共识机制的总称,其中包含了需要矿工做的一系列 SPoA 证明挑战。
为了理解这一点,我们将检查前一节中描述的 VDF 是如何被用来解锁 SPoA 挑战的。

以上代码详细表述了如何通过 VDF(加密时钟)来解锁存储分区中由一定 SPoA 数量组成的回溯范围的过程。
- 大约每秒钟,VDF 哈希链会输出一个检查点(Check);
- 这个检查点 Check 将与挖矿地址(addr),分区索引(index(p)),和原始 VDF 种子(seed)一起用 RandomX 算法计算出一个哈希值 H0,该哈希值是一个 256 位的数字;
- C1 是回溯偏移量,它是由 H0 除以分区的大小 size(p) 而产生一个余数得来,它将是第一个回溯范围的起始偏移量;
- 从这个起始偏移量开始的连续 100 MB 范围内的 400 个 256 KB 的数据块,就是被解锁出来的第一回溯范围 SPoA 挑战。
- C2 是第二回溯范围的起始偏移量,它是由 H0 除以所有分区大小之和而产生的余数得来的,它同样也解锁了第二回溯范围的 400 个 SPoA 挑战。
- 这些挑战的约束是第二范围内的 SPoA 挑战需要在第一个范围的对应位置也有 SPoA 挑战。
每个已打包分区的性能
每个已打包分区的性能指的是每个分区在每个 VDF 检查点所产生的 SPoA 挑战数量。当矿工存储的是分区唯一副本 Unique Replicas 时,SPoA 挑战数量将大于矿工存储相同数据的多个备份 Copies 时的数量。
这里的「唯一副本」概念与「备份」概念是有极大区别的,具体可以阅读过去的文章《Arweave 2.6 也许更符合中本聪的愿景》的内容。
如果矿工只存了分区的唯一副本数据,那每个打包过的分区将会产生所有第一回溯范围的挑战,然后根据存储分区副本的数量产生落在该分区内的第二回溯范围。若整个 Arweave 编织网络中共有 m 个分区,矿工存储了其中 n个分区的唯一副本,那么每个打包分区的性能为:
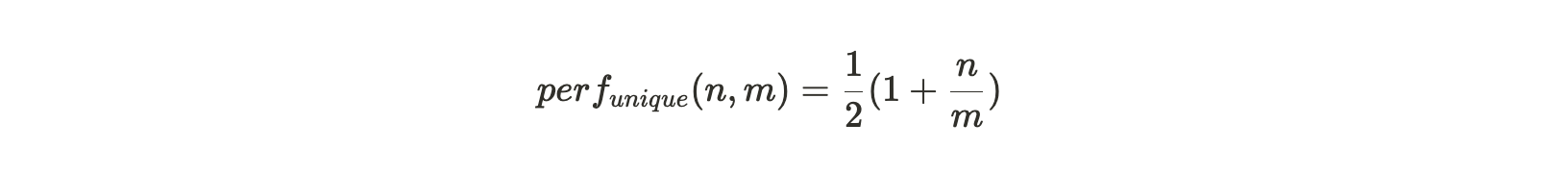
当矿工存储的分区是相同数据的备份时,每个打包过的分区仍然会产生所有第一回溯范围挑战。但只有在 1/m 次情况下,第二回溯范围会位于这个分区内。这便给这种存储策略行为带来了一个显著的性能惩罚,产生 SPoA 挑战数量的比率仅为:
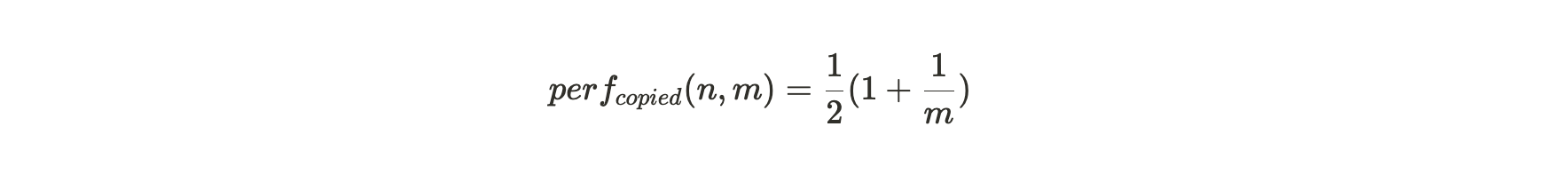
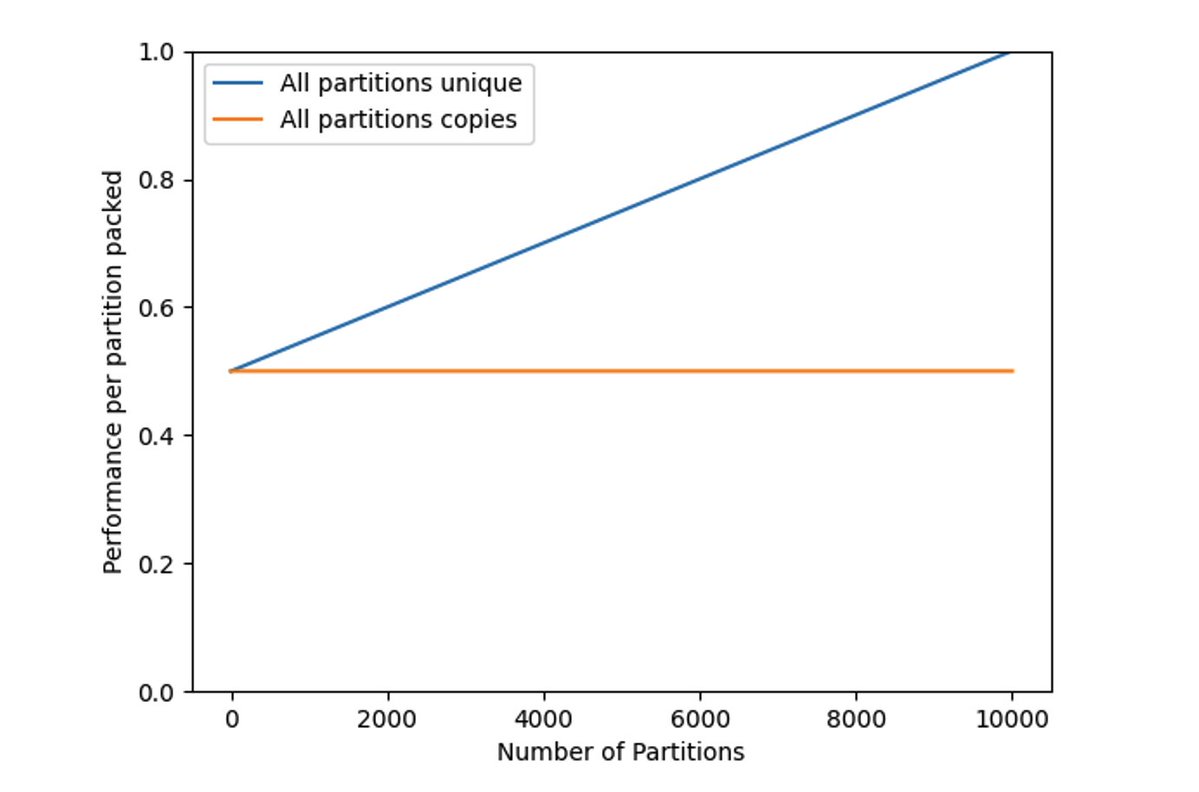
图 1:当一个矿工(或一组合作的矿工)完成打包他们的数据集时,给定分区的性能会提高。
图 1 中的蓝色线为存储分区唯一副本的性能 perf_{unique}(n,m) ,该图直观地表明了,当矿工只存储了很少的分区副本时,每个分区的挖矿效率仅为 50%。当存储和维护所有数据集部分,即 n=m 时,挖矿效率达到最大化的 1。
总哈希率
总哈希率(见图 2 所示)由以下方程给出,通过将每个分区(per partition)的值乘以 n 得到:
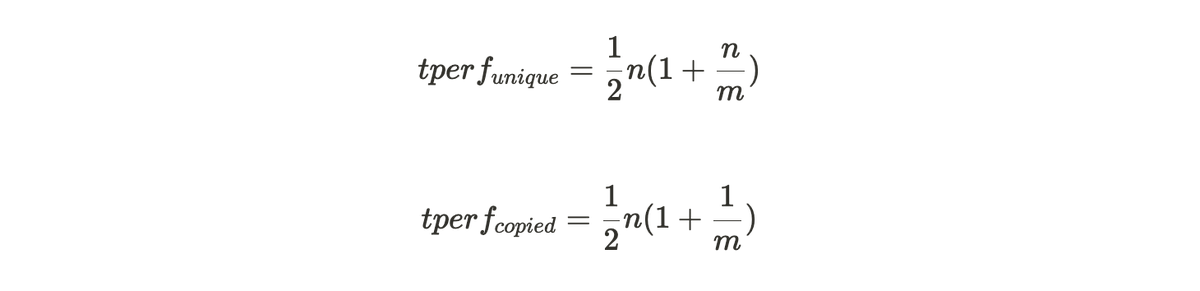
以上公式表明了随着编织网络(Weave)大小的增长,如果不存储唯一副本数据,惩罚函数(Penalty Function)随着存储分区数量的增加而呈二次方增长。
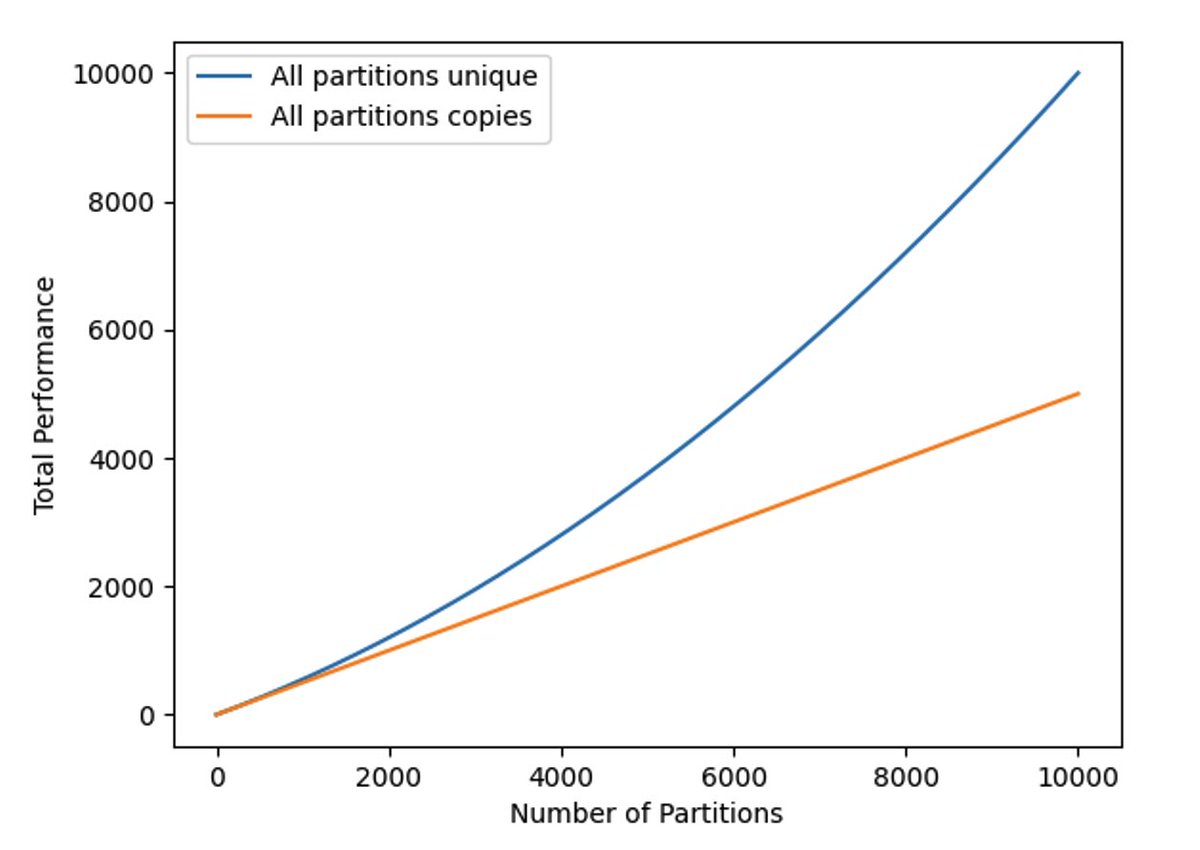
图 2:唯一数据集和备份数据集的总挖矿哈希率
边际分区效率
基于这个框架,我们来探讨矿工在添加新分区时面临的决策问题,即是选择复制一个他们已有的分区,还是从其他矿工那获取新数据并打包成唯一副本。当他们从最大可能的 m 个分区中已经存储了 n 个分区的唯一副本时,他们的挖矿哈希率是成比例的:
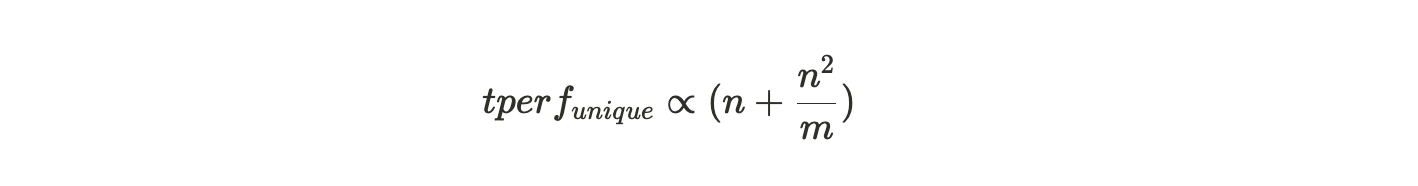
所以增加一个新分区的唯一副本,其额外收益为:
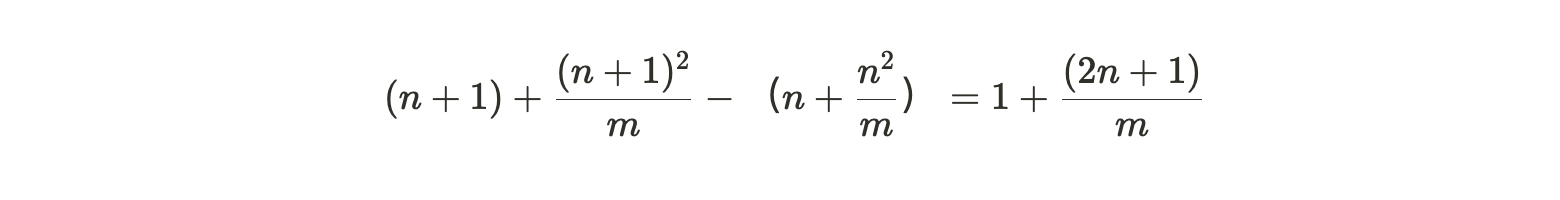
而复制一个已打包分区的(更小的)收益是:
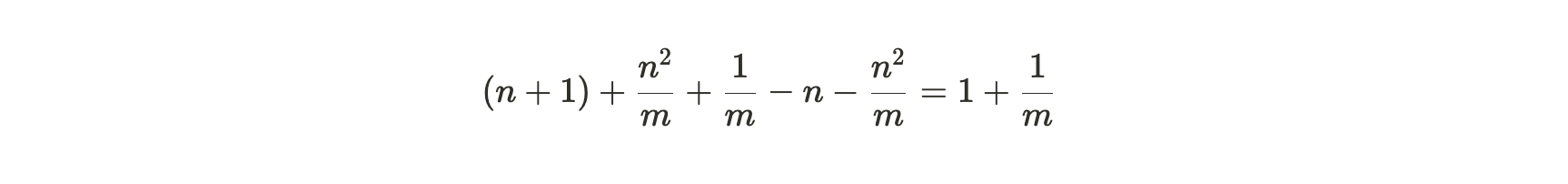
将第一个数量除以第二个数量,我们得到矿工的相对边际分区效率(relative marginal partition efficiency) :
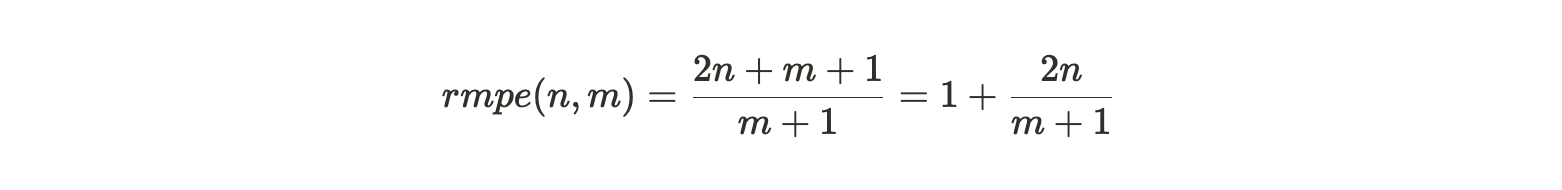
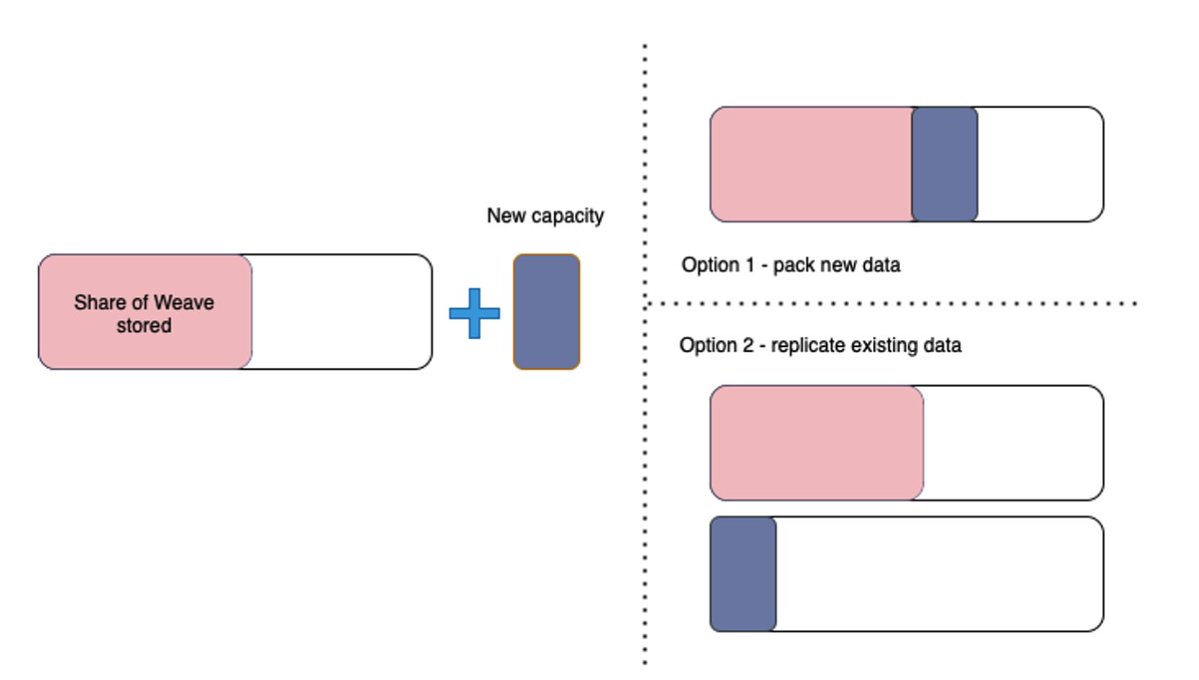
图 3:矿工被激励去构建成一个完整的副本(选项 1),而不是制作他们已经拥有的数据的额外副本(选项 2)
rmpe 值可被视为矿工在添加新数据时复制现有分区的一种惩罚。在这个表达式中,我们可以将 m 趋向无穷大来处理,然后再考虑不同 n 值下的效率权衡:
- 当矿工拥有接近完整数据集副本时,完成一个副本的奖励最高。因为如果 n 趋近于 m 并且 m 趋向于无穷大,则 rmpe 的值就为 3。这意味着,接近完整副本时,寻找新数据的效率是重新打包现有数据效率的 3 倍。
- 当矿工存储一半编织网络(Weave)时,例如,当 n= 1/2 m, rmpe 是 2。这表示寻找新数据的矿工收益是复制现有数据收益的 2 倍。
- 对于较低的 n 值,rmpe 值趋向于但总是大于 1。这意味着存储唯一副本的收益永远都是大于复制现有数据的收益。
随着网络的增长(m 趋向无穷大),矿工构建成完整副本的动力将会增强。这促进了合作挖矿小组的创建,这些小组共同存储至少一个数据集的完整副本。
✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨
本文主要介绍了 Arweave 共识协议构建的细节,当然这也只是这部分核心内容的开篇。从机制介绍与代码中,我们可以非常直观地了解到协议的具体细节。希望能够帮助大家理解。
原文链接:https://twitter.com/ArweaveOasis/status/1773174536546271563
- 原创
- 学分: 15
- 分类: Arweave/AO
- 标签: 去中心化存储 白皮书 SPoRes Aweave
- 什么是 Shelby 协议? 788 浏览
- 2026年展望:重构 - Heun的视角 228 浏览
- Web3 与去中心化存储 1981 浏览
- 密码朋克人物传之《Zcash创始人 Zooko Wilcox-O'Hearn》 1329 浏览
- 0G白皮书精读 3152 浏览
- 以太坊白皮书--知识总结 2510 浏览
- 📦 Web3 和区块链中的 IPFS:何时使用以及何时不使用 2559 浏览
- Walrus 协议 (WAL) 是什么 - 综合概述 1194 浏览
- 4EVERLAND 代币经济学:为全球 Web3 计算建立基础价值支柱 1858 浏览
- Unichain 白皮书 3479 浏览
- 去中心化存储的时空证明机制本质原理 4014 浏览
- 如何在 Permaswap 提供流动性赚钱 2891 浏览

