零知识证明
- Leo
- 发布于 2024-09-09 21:48
- 阅读 2483
零知识证明的概念:零知识证明技术可以[模拟]出一个第三方,保证某一个论断是可信的。举一个例子,我已经年满18岁已经成年了,我只要给出我的身份证(假设身份证上没有我的出生年月)。验证方也可以凭借此来判断我确实已经成年。而无需真实的知道我真实的出生年月零知识证明的使用场景:●数据的隐私保护
零知识证明的概念:
零知识证明技术 可以 [模拟]出一个第三方,保证某一个论断是可信的。 举一个例子,我已经年满18岁已经成年了,我只要给出我的身份证(假设身份证上没有我的出生年月)。验证方也可以凭借此来判断我确实已经成年。而无需真实的知道我真实的出生年月
零知识证明的使用场景:
● 数据的隐私保护:在一个数据表格中,多多少少都有一些信息不想被暴露,比如当年我的成绩单,我只想向人证明,我的成绩及格了,但是我不想让别人知道我到底考了61分还是62分,这会很尴尬。我没有心脏病,但是保险公司需要了解这一点,但是我不想让保险公司知道我的隐私信息。那我可以证明给保险公司看,我没有心脏病,但是病历的全部并不需要暴露。我是一家企业,我想向银行贷款,我只想向银行证明我具备健康的业务与还款能力,但是我不想让银行知道我们的一些商业秘密。 ● 计算压缩与区块链扩容:在众多的区块链扩容技术中,Vitalik 采用 zkSNARK 技术能够给现有的以太坊框架带来几十倍的性能提升。因为有了计算的证明,同样一个计算就没必要重复多次了,在传统的区块链架构中,同样的计算被重复多次,比如签名的校验,交易合法性校验,智能合约的执行等等。这些计算过程都可以被零知识证明技术进行压缩。 ● 端到端的通讯加密:用户之间可以互相发消息,但是不用担心服务器拿到所有的消息记录,同时消息也可以按照服务器的要求,出示相应的零知识证明,比如消息的来源、与发送的目的地。 ● 身份认证:用户可以向网站证明,他拥有私钥,或者知道某个只要用户自己才知道的秘密答案,而网站并不需要知道,但是网站可以通过验证这个零知识证明, 从而确认用户的身份 ● 去中心化存储:服务器可以向用户证明他们的数据被妥善保存,并且不泄露数据的任何内容。 ● 信用记录:信用记录是另一个可以充分发挥零知识证明优势的领域,用户可以有选择性的向另一方出示自己的信用记录,一方面可以有选择的出示满足对方要求的记录分数,同时证明信用记录的真实性。 ● 构造完全公平的线上数字化商品的交易协议[9]。 ● 更多的例子,可以是任何形式的数据共享,数据处理与数据传输。 下面引用『Foundations of Cryptography—— Basic Tools』一书[10]中的总结
- 「知识」是与「计算难度」相关,而「信息」则不是
- 「知识」是与公共所知的东西有关,而「信息」主要与部分公开的东西有关
通过地图三染色问题来阐述
下面我们设计一个交互协议: ● 「证明者」Alice ● 「验证者」 Bob Alice 手里有一个地图三染色的答案,请见下图。这个图总共有 6 个顶点,9 条边。
 现在 Alice 想证明给 Bob 她有答案,但是又不想让 Bob 知道这个答案。Alice 要怎么做呢?
Alice 先要对染过色的图进行一些「变换」,把颜色做一次大挪移,例如把所有的绿色变成橙色,把所有的蓝色变成绿色,把所有的绿色变成橙色。然后 Alice 得到了一个新的染色答案,这时候她把新的图的每一个顶点都用纸片盖上,然后出示给 Bob 看。
现在 Alice 想证明给 Bob 她有答案,但是又不想让 Bob 知道这个答案。Alice 要怎么做呢?
Alice 先要对染过色的图进行一些「变换」,把颜色做一次大挪移,例如把所有的绿色变成橙色,把所有的蓝色变成绿色,把所有的绿色变成橙色。然后 Alice 得到了一个新的染色答案,这时候她把新的图的每一个顶点都用纸片盖上,然后出示给 Bob 看。
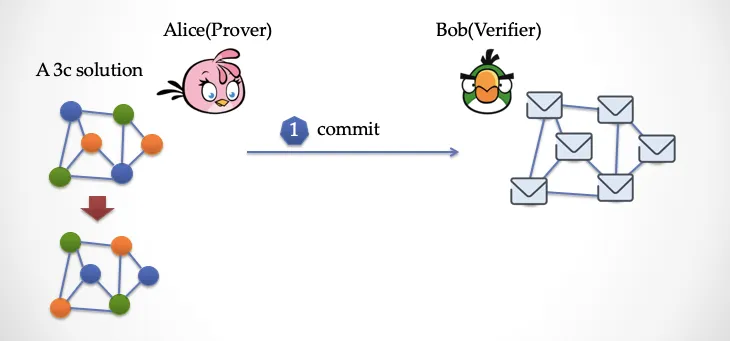 看下图,这时候 Bob 要出手了(请见下图),他要随机挑选一条「边」,注意是随机,不让 Alice 提前预测到的随机数。
看下图,这时候 Bob 要出手了(请见下图),他要随机挑选一条「边」,注意是随机,不让 Alice 提前预测到的随机数。
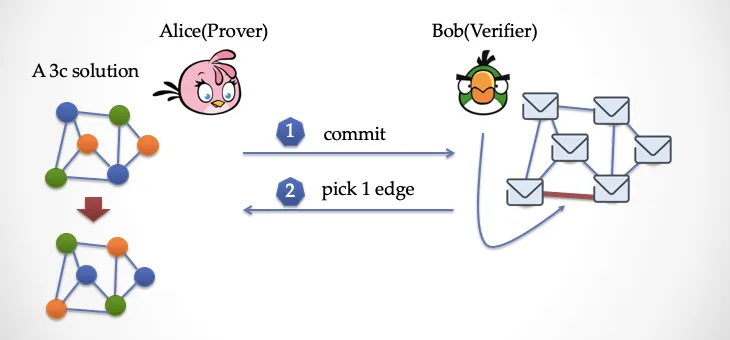 假设 Bob 挑选的是最下面的一条边,然后告诉 Alice。
假设 Bob 挑选的是最下面的一条边,然后告诉 Alice。
这时候 Alice 揭开这条边两端的纸片,让 Bob 检查,Bob 发现这两个顶点的颜色是不同的,那么 Bob 认为这次检验同构。这时候,Bob 只看到了图的局部,能被说服剩下的图顶点的染色都没问题吗?你肯定觉得这远远不够,也许恰好 Alice 蒙对了呢?其它没暴露的顶点可能是胡乱染色的。 没关系,Bob 可以要求 Alice 再来一遍,看下图
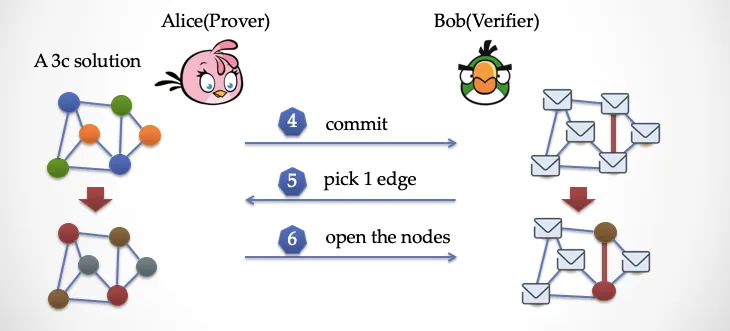 Alice 再次把颜色做一次变换,把蓝色改成紫色,改绿色改成棕色,把橙色改成灰色,然后把所有的顶点盖上纸片。然后 Bob 再挑选一条边,比如像上图一样,选择的是一条竖着的边,然后让 Alice 揭开纸片看看,如果这时候 Bob 再次发现这条边两端的顶点颜色不同,那么 Bob 这时候已经有点动摇了,可能 Alice 真的有这个染色答案。可是,两次仍然不够,Bob 还想再多来几遍。
那么经过反复多次重复这三个步骤,可以让 Alice 作弊并能成功骗过 Bob 的概率会以指数级的方式减小。假设经过 n 轮之后,Alice 作弊的概率为Pr[(G,c) ∣ ThreeColor(G,c)=0]<(1−1∣E∣)nPr[(G,c) ∣ ThreeColor(G,c)=0]<(1−∣E∣1)n
这里 |E| 是图中所有边的个数, 如果 n 足够大,这个概率 Pr 会变得非常非常小,变得「微不足道」。
可是,Bob 每次看到的局部染色情况都是 Alice 变换过后的结果,无论 Bob 看多少次,都不能拼出一个完整的三染色答案出来。实际上,Bob 在这个过程中,虽然获得了很多「信息」,但是却没有获得真正的「知识」。
以上案例,大致描述了零知识证明的大致逻辑
Alice 再次把颜色做一次变换,把蓝色改成紫色,改绿色改成棕色,把橙色改成灰色,然后把所有的顶点盖上纸片。然后 Bob 再挑选一条边,比如像上图一样,选择的是一条竖着的边,然后让 Alice 揭开纸片看看,如果这时候 Bob 再次发现这条边两端的顶点颜色不同,那么 Bob 这时候已经有点动摇了,可能 Alice 真的有这个染色答案。可是,两次仍然不够,Bob 还想再多来几遍。
那么经过反复多次重复这三个步骤,可以让 Alice 作弊并能成功骗过 Bob 的概率会以指数级的方式减小。假设经过 n 轮之后,Alice 作弊的概率为Pr[(G,c) ∣ ThreeColor(G,c)=0]<(1−1∣E∣)nPr[(G,c) ∣ ThreeColor(G,c)=0]<(1−∣E∣1)n
这里 |E| 是图中所有边的个数, 如果 n 足够大,这个概率 Pr 会变得非常非常小,变得「微不足道」。
可是,Bob 每次看到的局部染色情况都是 Alice 变换过后的结果,无论 Bob 看多少次,都不能拼出一个完整的三染色答案出来。实际上,Bob 在这个过程中,虽然获得了很多「信息」,但是却没有获得真正的「知识」。
以上案例,大致描述了零知识证明的大致逻辑
接下来我们来分析zkSNARK
ZK-SNARKs的特征
- 零知识(Zero-knowledge):这意味着验证者除了知道声明的有效性或虚假之外,一无所知。 2 . 简洁(Succinct):证明足够小,验证者可以在短时间内完成验证。
- 非交互式(Non-interactive):SNARKs 是非交互式的,因为证明者和验证者不需要交换超出提交的初始证明之外的信息。早期的零知识证明系统需要证明者和验证者交换多条消息来验证陈述。
- 论证(Argument):SNARK 是一个满足严格要求的“计算合理”的陈述,因此很难作弊(即生成虚假证明)。
- 知识:基于 SNARK 的证明不能通过访问底层信息或见证来创建。
ZK-SNARKs 和 ZK rollups
汇总(rollup)是以太坊的第 2 层扩展解决方案,可通过链下执行提高L1区块链的吞吐量。汇总 处理 L2 链上的交易,将多个链下交易聚合成区块,并提交给 L1 链。 通过将计算从基础层移开,汇总可以减少网络拥塞并扩展交易。 然而,L1 链需要知道链下执行的交易是否有效(即计算完整性问题)。否则,恶意行为者可以劫持汇总并向主链提交不良交易。 一种类型的汇总(零知识汇总)使用 ZK-SNARKs 向 L1 链证明链下交易的真实性。任何人都可以验证 SNARK 证明,这确保了 L1 链的交易有效性。
- L2 链上的用户签署交易并将其提交给验证者。
- 验证者将交易压缩成一个区块,并生成相应的有效性证明(SNARK)。这提供了新状态由添加有效交易产生的加密保证。
- L1 链上的智能合约对有效性证明进行操作。此操作的结果确定批量交易是否经过验证并发布到主链。
ZK-SNARKs的缺点
- 可信设置 (Trusted setup ) 设置 ZK-SNARK 协议需要创建一个通用公共参考字符串 (CRS:Common Reference String)。CRS也被描述为公共参数,它支持证明者和验证者之间的安全通信。 如果恶意行为者获得了公共参数的知识,他们可能会生成虚假的有效性证明。一些项目试图通过涉及不同个体的多方计算(MPC:multi-party computation )来生成公共参数来解决这个问题。 然而,这种方法要求用户信任涉及到各方的完整性。这有很大的问题,因为区块链的目的是减少对信任机构的需求。
- 易受量子计算攻击 ZK-SNARK 使用椭圆曲线密码体制 (ECC:Elliptic Curve Cryptography) 来加密用于生成有效性证明的信息。ECC 目前相对安全,但量子计算的进步可能会打破其安全模型。 3.对特殊硬件的依赖 使用 ZK-SNARKs 生成有效性证明是一个计算密集型过程,这意味着证明者必须使用专门的硬件。因为很少有人能买到这些机器,所以很多人认为 ZK-SNARK 证明过程是高度中心化的。
简单结合着一个多项式案例来看
x^3+x+5 = 35(这个方程的解是x=3,因为3**3+3+5 = 35)来举例说明将目标计算问题转换为一个QAP的过程。
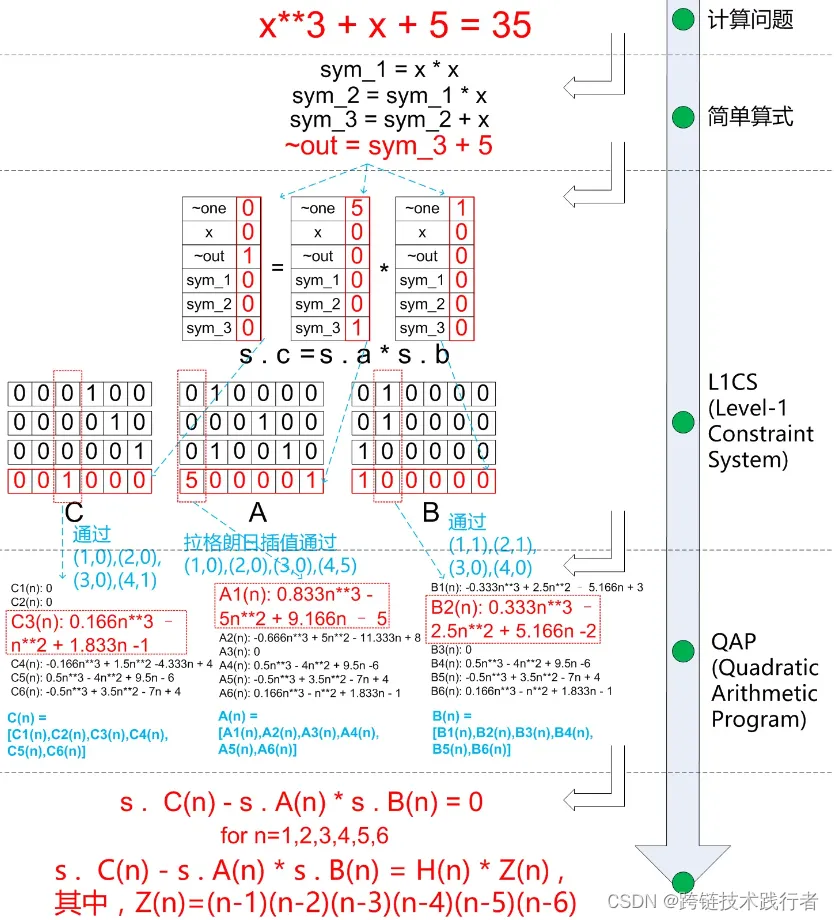
第一步 通过引入中间变量,将计算式x^3+x+5转换为若干简单算式。这些简单算式要么是“x = y”或者“x = y (op) z”的形式。操作符“op”代表加(+)、减(-)、乘()和除(/)。这些简单算式可视为数字电路中的逻辑门,因此也被称为“代数电路(Algebraic Circuit)”。图10例中引入的中间变量是sym_1、sym_2和sym_3; 第二步 定义向量s=[~one, x, ~out, sym_1, sym_2, sym_3](~one是伪变量,表示常数1),将每个简单算式转换为“s . c = s . a s . b”的形式。其中,“."代表向量内积(将两个向量对应位置的成员相乘,结果再累加),a、b和c是其系数向量。依次完成所有简单算式的转化,将系数向量分别顺序排列,便得到A、B和C三个矩阵(例如,矩阵C的最后一行,就是简单算式“~out = sym_3 + 5”的系数向量c)。这个描述形式有个专门的术语,称作"一阶约束系统(L1CS)”。满足所有约束条件的向量s就是问题的解;
第三步,将每个矩阵压缩为一个多项式组成的向量,例如矩阵C → C(n)=[C1(n), C2(n), C3(n), C4(n), C5(n), C6(n)]。方法是:对矩阵的每一列分别运用拉格朗日插值法。譬如,矩阵C的第3列为[0,0,0,1],现在要求取一个多项式C3(n),使得n分别取1、2、3、4时,C3(n)的值为:
| n | C3(n) |
|---|---|
| 1 | 0 |
| 2 | 0 |
| 3 | 0 |
| 4 | 1 |
按照拉格朗日插值法,C3(n)可以分解为4个部分之和:
C3_1(n) = A(n-2)(n-3)(n-4) C3_2(n) = B(n-1)(n-3)(n-4) C3_3(n) = C(n-1)(n-2)(n-4) C3_4(n) = D(n-1)(n-2)(n-3) C3(n) = C3_1(n) + C3_2(n) + C3_3(n) + C3_4(n) 按照图标,已知n = 4时,C3(n) = 1。因为,n = 4时,C3_1(n)、C3_2(n)和C3_3(n)分别为0,因此,C3_4(4) = D(4-1)(4-2)(4-3) = 1,从而得到D = 1/6。同理,A = B = C = 0。于是,可知C3(n) = 1/6(n-1)(n-2)*(n-3) = 0.166n3-n2+1.833n-1。
求得多项式向量A(n)、B(n)和C(n)后,计算问题便转换为求取解向量s,使得等式s . C(n) - s . A(n) s . B(n) = 0 在n=1,2,3,4,5,6时成立,等价于: s . C(n) - s . A(n) s . B(n) = H(n) * Z(n),其中, Z(n) = (n-1)(n-2)(n-3)(n-4)(n-5)(n-6)。各位请注意: 方程式中如愿以偿地出现了多项式! 解的形式并不会随着算式发送改变 s = [~one, x, ~out, sym_1, sym_2, sym_3] = [1, 3, 35, 9, 27, 30] 通过上述的一系列转换,我们可以向“零知识”证明目标靠近 假设证明人想知道原始问题“x*3+x+5 = 35”的解,如果不对问题进行转化,证明人为了自证,好像除了公布解(x=3),似乎也没有别的办法。然而,问题转化为求解“s . C(n) - s . A(n) s . B(n) = H(n) Z(n)”后(其中,系数向量A(n)、B(n)和C(n)是公开的),证明人知道解s,计算多项式P(n)和H(n) = P(n)/Z(n),后将两个多项式P(n)、H(n)发给验证者()。通过检查P(n) ?= H(n) Z(n)是否成立来判断A证明人是否真的知道解。这样其实也就是零知识证明的一种手段了。
当然,要更深入的了解零知识证明,还需要细致了解 多项式原理,QAP和椭圆曲线原理
引用文档: https://secbit.io/blog/2019/07/31/zero-knowledge-and-proof/ https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649 https://blog.csdn.net/shangsongwww/article/details/89529559
- Zero 链: 技术定位报告 77 浏览
- 以太坊亟需的两大深度改造——二进制树 + VM 改造 75 浏览
- 以太坊 2029 Strawmap 傻瓜指南 162 浏览
- 不实的断言:攻破 6 个 zkVMs 94 浏览
- zERC20 在 Arbitrum 上线:最完备 L2 的原生隐私 201 浏览
- 零知识编年史:群 158 浏览
- 以太坊执行层优化:状态树与虚拟机 332 浏览
- 首批 ZK 漏洞利用事件已发生,但它们并非我们所预期 257 浏览
- 首次 ZK 攻击发生,且出乎意料 268 浏览
- Vitalik: 以太坊量子抵抗路线图 230 浏览
- zkMesh:2026年2月回顾 284 浏览
- 失效的 Groth16 `delta == gamma == G2 生成元` 291 浏览

