BLS签名、BLS12-381椭圆曲线以及基于配对签名方案的剖析

BLS 签名，BLS12–381 椭圆曲线及基于配对的签名方案结构。

在上一篇文章中，我们讨论了第一类数字签名方案，具体来说是基于椭圆曲线的方案。在这篇文章中，我们将探索第二类方案，基于配对的方案，例如 BLS 签名。BLS 签名以其高效性和安全性而闻名。基于配对的方案与基于椭圆曲线的方案在基础加密学上有所不同；它们依赖于椭圆曲线上的配对和双线性映射，而不是后者中使用的标量乘法。配对和双线性映射使 BLS 签名方案能够支持高级加密技术，例如签名聚合。BLS 签名在签名小型化及验证所需的低计算量方面也非常高效。因此，它在其他高级协议中得到了广泛应用，如 KZG 多项式承诺和零知识证明 (ZKP)。让我们开始吧！

配对

这一部分重温一下椭圆曲线配对的知识。我们在我关于“高级加密原语”的文章中讨论了这个话题。然而，我相信在这里回顾一下是有价值的。

配对是一种高级加密操作，它将椭圆曲线 G_1 和 G_2 上的两个点映射到目标有限域 G_T 中的一个元素。用 e 表示。

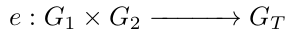
需要注意的是，配对仅在配对友好的椭圆曲线上成立，例如 BLS12–381，而不是任何椭圆曲线。

配对具有一个独特的属性，称为“ 双线性映射”，其表达如下。

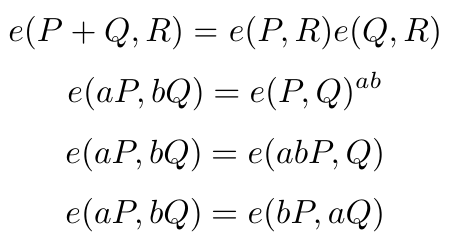
其中：

• P, Q, R — 椭圆曲线上的点
• a, b — 整数

双线性映射意味着我们可以在曲线上“移动”系数 a, b，同时保持映射结果等于 e(P, Q)^(ab)。这个属性在 BLS 签名方案中至关重要。

BLS12–381 椭圆曲线

BLS12–381 是一种广泛应用于 BLS 签名的椭圆曲线。如上所述，BLS12–381 是一种配对友好的椭圆曲线。曲线的理论形式如下图所示。

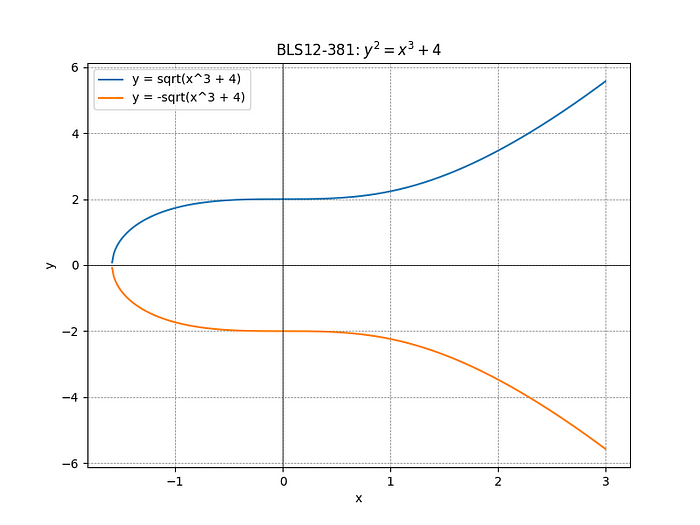
BLS12–381 的理论形式。

方程

BLS12–381 是一种韦伊斯特拉斯曲线，类似于 secp256k1。曲线上的点满足以下方程。

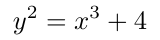
有限域

为了支持配对操作，BLS12–381 曲线定义在两个域上：

• 基域 F_q 是一个素数域，q=2³⁸¹-19
• 扩展域 F_q² 是一个复数域，元素表示为 a+bi；其中 a, b 是来自 F_q 的元素，i 是虚数单位，满足 i²=-1

可以将其认为 BLS12–381 由两个椭圆曲线 E_1 和 E_2 组成，定义如下。

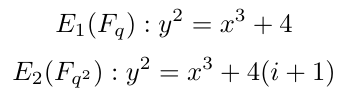
群

回想一下，BLS12–381 是一种配对友好的椭圆曲线。这意味着它将 E_1 和 E_2 上的两个点 G_1 和 G_2 作为输入。配对操作将这些点映射到目标有限域中的元素。点 G_1 和 G_2 的 x 和 y 坐标分别是基域 F_q 和扩展域 F_q² 的元素。实际上，它们是 F_q 和 F_q² 的子群元素。这些子群具有相同的阶，记为 r。配对目标也是一个阶为 r 的群。r 是一个素数，等于 r=2²⁵⁵-19。

你可能注意到，基域 F_q 只有阶为 r 的一个子群，因此不能仅基于 F_q 定义配对。为了定义椭圆曲线 E_2 和目标域，我们需要使用一种称为“ 域扩展”的技术。实际上，基域 F_q 被扩展到 F_q¹²，满足两个条件。

• F_q¹² 包含多个阶为 r 的子群
• F_q¹² 包含所有 r 次单位根，这些根是元素 e，满足 e^r=1。单位根对于需要多项式运算的加密协议至关重要。

数字 12 是最小的整数 k，使得 r 整除 (q^k-1)。它被称为曲线的 嵌入度。

然而，在扩展域 F_q¹² 上定义的椭圆曲线 E_2 在曲线操作方面效率较低。BLS12–381 使用“六次扭转”将扩展域的度数降低了 6 倍。因此，椭圆曲线 E_2 可以在域 F_q² 上定义，这在加密方面更高效。

基群

G_1 是基域 F_q 中阶为 r 的一个子群。

基群 G_1 的生成点是 g_1(x, y)，其中：

x = 3685416753713387016781088315183077757961620795782546409894578378688607592378376318836054947676345821548104185464507

y = 1339506544944476473020471379941921221584933875938349620426543736416511423956333506472724655353366534992391756441569

基群 G_1 的余因子 h=0x396c8c005555e1568c00aaab0000aaab

扩展群

G_2 是扩展域 F_q² 中阶为 r 的一个子群。

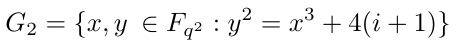
扩展群 G_2 的生成点是 g_2(x, y)，其中：

x = 3059144344244213709971259814753781636986470325476647558659373206291635324768958432433509563104347017837885763365758*u + 352701069587466618187139116011060144890029952792775240219908644239793785735715026873347600343865175952761926303160

y = 927553665492332455747201965776037880757740193453592970025027978793976877002675564980949289727957565575433344219582*u + 1985150602287291935568054521177171638300868978215655730859378665066344726373823718423869104263333984641494340347905

扩展群 G_2 的余因子 h=0x5d543a95414e7f1091d50792876a202cd91de4547085abaa68a205b2e5a7ddfa628f1cb4d9e82ef21537e293a6691ae1616ec6e786f0c70cf1c38e31c7238e5。

与非配对的椭圆曲线（如 secp256k1 或 Curve25519）不同，BLS12–381 中的 G_1 和 G_2 的群余因子确实非常大。

目标群

如上所述，扩展域 F_q¹² 包含所有 r 次单位根。这些 r 次单位根实际上形成一个阶为 r 的子群，即目标群 G_T。

BLS 签名方案

BLS 签名方案是一种基于配对的签名方案，利用 BLS12–381 椭圆曲线。它提供 128 位安全性，由于签名小型化及其支持签名聚合的能力而具有高度的效率。让我们深入了解签名过程。

签名生成

假设 Alice 想为一条消息 m 创建 BLS 签名，然后由 Bob 验证。

首先，Alice 需要通过从基域 F_q 中随机抽样生成一个私钥 a。实际上，a 是 1 和 r-1 之间的一个随机值。完成后，她通过将其私钥 a 乘以生成器 G_1 来推导公钥 A。

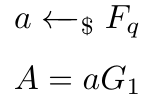
现在，Alice 需要将她想签名的消息 m 转换为一个能够“映射到”椭圆曲线 E_2 的表示。这可以通过使用安全的哈希函数 H（例如 SHA-256）对 m 进行哈希实现。这个哈希值表示为 z。

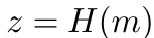
最后，Alice 通过将她的私钥 a 与哈希值 z 相乘来生成签名。

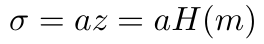
然后，她将签名、她的公钥 A 和消息 m 发送给 Bob 进行验证。

签名验证

为验证签名，Bob 只需检查是否满足：

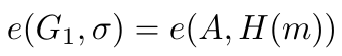
该协议如下面的图所示。

为什么它有效

利用配对操作的双线性映射特性，我们得到：

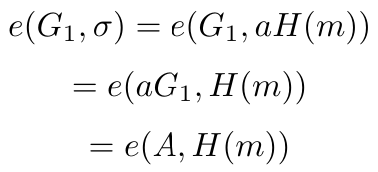
这意味着方程成立，因此签名是有效的。协议的正确性得到了证明。

安全级别

BLS 签名的安全级别为 128 位，这意味着在理论上要暴力破解签名系统需要 2¹²⁸ 次操作。具体而言，这涉及尝试通过在有限域 F_q 中搜索所有可能的元素来推导私钥。然而，这种攻击在实际操作中是不可行的，128 位安全级别被认为对当前的计算能力是安全的。

代码示例

下面分享了一个 BLS 签名的代码示例。

signature-schemes/pairings/bls.py at main · 0xbarchitect/signature-schemes \ \ 流行签名方案的实验代码，包括 BLS、ECDSA 和 EdDSA。…\ \ github.com

BLS 签名聚合

BLS 签名方案一个重要的价值主张是其能够支持签名聚合。具体而言，验证由 n 方签名的单个消息仅需要两个配对，或者验证由 n 方签名的 n 个不同消息需 n+1 个配对。由于配对的计算成本很高，因此这一能力备受青睐。

假设我们有 n 方，每方都有自己的私钥 a_i，对应的公钥为 A_i=a_i*G_1。每方按如下方式签名自己的消息 m_i。

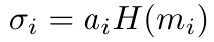
这里 H 是哈希函数。

现在，在验证时，我们希望验证一个单一的聚合签名，而不是逐个验证 n 个签名。这不仅减少了计算量，还节省了通过网络传输这些签名的带宽。

为了达到这个目的，我们计算聚合签名如下。

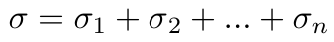
要验证聚合签名，我们检查是否满足：

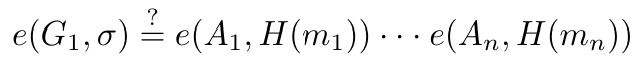
这是为什么呢？利用双线性映射，我们可以证明。

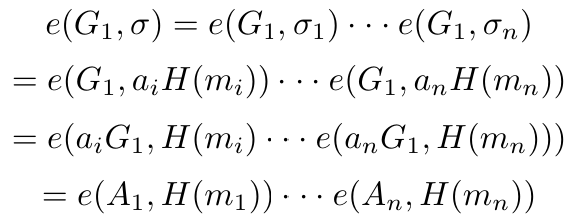
这意味着方程成立，因此，聚合签名是有效的。此外，每个单独的签名也是有效的。因此，BLS 签名方案能够将 n 个签名聚合成一个等效的聚合签名。这一能力对于实施多项式承诺方案（如 KZG），或实施零知识证明（如 zkSNARKs）至关重要。

代码示例

下面分享了一个 BLS 签名聚合的代码示例。

signature-schemes/pairings/bls_aggregation.py at main · 0xbarchitect/signature-schemes \ \ 流行签名方案的实验代码，包括 BLS、ECDSA 和 EdDSA。…\ \ github.com

MOV 攻击

对于配对友好的椭圆曲线，例如 BLS12–381，存在一种针对椭圆曲线上离散对数问题（DLP）的攻击。该攻击称为 MOV 攻击，名称源于发现此攻击的密码学家：Menezes、Okamoto 和 Vanstone。

回顾有限域 F_q 上的椭圆曲线 E 中的 DLP：给定曲线上的点 A 和生成器 G，寻找有限域中的数字 a，使得 A=aG。

该攻击的工作原理如下：假设 B 是 E 中的另一个点，我们可以与 A 配对。我们有：

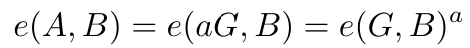
注意到 e(A, B) 和 e(G, B) 都在目标域 F_t 中。我们不再解决椭圆曲线中的离散对数问题，而是在以下域上解决同样的问题。

给定：

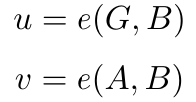
找到一个 a 使得。

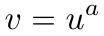
一般而言，有限域上的离散对数问题比椭圆曲线上的离散对数问题更容易，因此对于具有配对的椭圆曲线，系统的安全性降低。

结论

BLS 签名是基于 BLS12–381 椭圆曲线的配对签名方案。它提供 128 位安全级别，以其在加密效率上的表现，尤其是支持签名聚合的能力而闻名。BLS 签名在其他高级密码协议中广泛应用，如多项式承诺和零知识证明。

需要注意的是，BLS12–381 椭圆曲线与非配对椭圆曲线不同，尤其在于其扩展域和曲线内存在两个椭圆曲线。在我看来，BLS12–381 的加密学比 non-pairings 曲线（如 secp256k1 或 Curve25519）复杂得多。这种复杂性是可以理解的，因为该曲线支持配对操作。然而，配对也引入了针对这些椭圆曲线的 DLP 攻击向量，特别是 MOV 攻击。因此，使用 BLS 签名时应充分意识到这些潜在的脆弱性。

如果你觉得这篇文章有价值，请关注我。这样会让我感到开心，并激励我写出更多优质的文章。非常感谢你的支持 🙏

参考文献

1. 0xbarchitect — 高级加密原语
2. 0xbarchitect — Diffie-Hellman 问题
3. Nguyen Thoi Minh Quan — 直观的高级加密
4. Ben Edgington — BLS12–381 为了我们
5. Philipp Muens — BLS 签名

• 原文链接： medium.com/@barchitect/b...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～