掌握SP1 zkVM设计 - 第二部分:核心证明的AIR约束
- gavin.ygy
- 发布于 2025-02-19 13:40
- 阅读 2664
本文深入探讨了SP1 zkVM设计中的核心证明及其约束系统,详细介绍了如何使用AIR(代数中间表示)来表示计算过程,并通过多项式约束确保状态转移的正确性。文章还介绍了SP1 zkVM中的预编译技术,用于加速常见操作如哈希计算和椭圆曲线运算。
1. SP1 证明种类
(1) 核心证明
SP1 的第一阶段证明结果。客户程序可以被划分为多个 shard, 每个 shard 通过 zkVM 生成一个 STARK 证明。因此,核心证明可能包含一组 ShardProofs。
(2) 压缩证明
核心证明(一个 ShardProofs 向量)通过 FRI 递归算法 压缩为单个 ShardProof。
(3) Snark 证明
压缩证明进一步使用 Plonk 算法 或 Groth16 算法(在 Bn254 曲线上)进行压缩,生成 Plonk(Bn254)证明或 Groth16(Bn254)证明。
示例(基于 CPU 的证明生成):
在 sp1/crates/sdk/src/prover/cpu.rs 中,prove() 函数根据配置生成不同类型的证明。例如,要生成压缩证明,客户可以如下调用:client.prove(&fibonacci_pk, stdin).compressed().run().expect(“prove 失败”))。
fn prove<'a>(
&'a self,
pk: &SP1ProvingKey,
stdin: SP1Stdin,
opts: ProofOpts,
context: SP1Context<'a>,
kind: SP1ProofKind,
) -> Result<SP1ProofWithPublicValues> {
// 生成核心证明。
//…
if kind == SP1ProofKind::Core {
return Ok(SP1ProofWithPublicValues {
proof: SP1Proof::Core(proof.proof.0),
stdin: proof.stdin,
public_values: proof.public_values,
sp1_version: self.version().to_string(),
});
}
//…
if kind == SP1ProofKind::Compressed {
return Ok(SP1ProofWithPublicValues {
proof: SP1Proof::Compressed(Box::new(reduce_proof)),
stdin,
public_values,
sp1_version: self.version().to_string(),
});
}
// 生成缩减证明。
//…
if kind == SP1ProofKind::Plonk {
//…
return Ok(SP1ProofWithPublicValues {
proof: SP1Proof::Plonk(proof),
stdin,
public_values,
sp1_version: self.version().to_string(),
});
} else if kind == SP1ProofKind::Groth16 {
//..
return Ok(SP1ProofWithPublicValues {
proof: SP1Proof::Groth16(proof),
stdin,
public_values,
sp1_version: self.version().to_string(),
});
}
unreachable!()
}2. AIR 约束系统
2.1 基本概念
AIR(代数中间表示)是用于表示计算的执行轨迹的一种代数形式。它将计算过程分解为一系列状态转换,并通过多项式约束确保这些转换的正确性。AIR 的核心思想是将计算问题转化为多项式方程,从而利用零知识证明技术进行验证。
- 执行轨迹:AIR 将计算过程表示为一个二维矩阵,其中每一行对应于一步计算的状态,每一列表示一个状态变量。
- 约束:AIR 使用多项式方程定义状态转换的规则,以确保计算的正确性。包括初始状态约束、状态转换约束和最终状态约束。
2.2 Plonky3 AIR 的核心组件
(1) BaseAir 和 Air
- BaseAir:定义 AIR 的基本属性,例如轨迹的宽度(即每行的列数)。
- Air:定义特定的约束条件,通过
eval函数实现。eval函数使用AirBuilder工具来构建约束。
(2) 约束构建工具
主要构建器如下:
- AirBuilder(
p3/air/src/air.rs):定义多项式约束的核心接口,实现一些常用方法。 - PermutationAirBuilder(
p3/air/src/air.rs):用于验证两个轨迹是否为相互的排列。 - DebugConstraintBuilder(
p3/uni-stark/src/check_constraints.rs):检查 AIR 约束是否被正确满足,当约束不满足时通过断言快速识别错误。 - SymbolicAirBuilder(
p3/uni-stark/src/symbolic_builder.rs):主要用于分析约束的符号形式并确定商多项式的度数。 - ProverConstraintFolder(
p3/uni-stark/src/folder.rs):主要用于构建约束多项式的商多项式。
2.3 在 SP1 中实现 AIR
(1) MachineAir
MachineAir(sp1/stark/src/air/machine.rs)扩展了 Plonky3 的 BaseAir,作为 SP1 约束的核心组件。它添加了获取芯片(AIR)名称、生成执行轨迹、为记录中的每个芯片生成 ByteLookupEvent,以及在设置阶段生成预处理轨迹的方法。SP1 中所有芯片必须实现 MachineAir。
(2) 约束构建工具
- BaseAirBuilder(
stark/src/air/builder.rs)扩展了 Plonky3 的AirBuilder。SP1 中的大多数构建器直接或间接继承自BaseAirBuilder。 - InteractionBuilder(
stark/src/lookup/builder.rs):专门为查找表构建约束。 - ProverConstraintFolder(
stark/src/folder.rs):SP1 不使用 Plonky3 的ProverConstraintFolder,而是重新定义它以构建商多项式。
(3) 芯片 Chip
SP1 zkVM 实现了 39 条 RISC-V 指令,每条指令生成一个事件,每个事件对应一个 Chip(AIR 约束)。一些指令事件共享相同的约束;例如,加法和减法指令都由 AddSubChip 约束。SP1 中的所有事件都在结构体 ExecutionRecord(core/executor/src/record.rs)中定义。其中,CpuEvent 是核心事件,包含客户程序的所有指令。此外,为 CPU 事件中的指令定义了 ProgramChip 约束,以跟踪在 CpuEvents 中指令的出现次数。与指令事件相关的代码位于 core/executor/src 中,而与芯片约束相关的代码则在 core/machine/src 中。
在 SP1 zkVM 的证明开始时,Execution Record 中包含的事件被顺序转换为相应的芯片轨迹,即添加到该轨迹的 RowMajorMatrix 中。有关预编译事件的更多详细信息,请参见第 3 节。预编译。
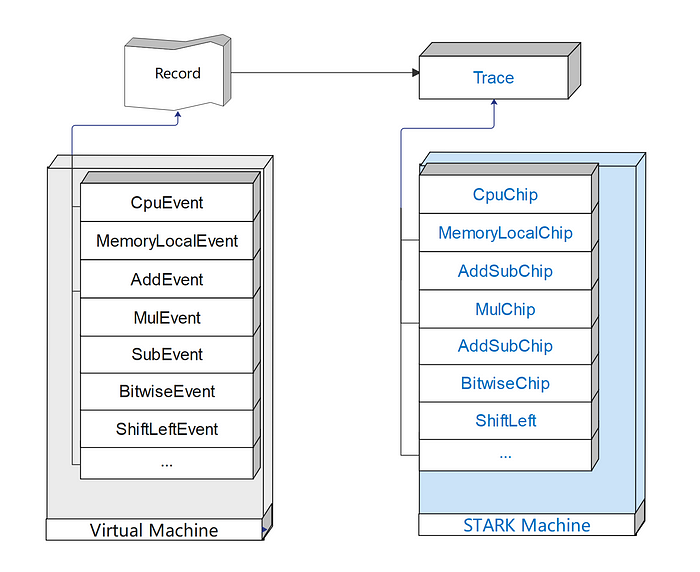
图 1 SP1 zkVM 事件与相应的 STARK 芯片(AIR)
(4) 主轨迹列
每个芯片的(主)轨迹列的结构通常与相应事件的结构一致,只是轨迹矩阵使用的是 Babybear 字域元素(以 Montgomery 表示),而事件使用的是 Rust 数据类型。
(5) Eval
每个芯片必须实现 eval 函数,定义芯片的约束并验证执行轨迹的每一行是否满足这些约束。
(6) 排列轨迹
SP1 具有多个芯片(AIR),每个芯片有一个主轨迹(表)。某些芯片还具有预处理轨迹(表)。每当表 𝑇 需要在另一表中或内存中查找某些东西时,𝑇 会“发送”请求,而后者会“接收”请求。SP1 基于 LogUp 查找协议,引入了多重性:发送表(轨迹) T 被划分为更小的矩阵 A_{ij}^{(1)}, A_{ij}^{(2)}, … , A_{ij}^{(k)}。这些更小的矩阵的第 i 行在接收矩阵 B 的第 i 行中出现的次数称为多重性 ( m_i)。SP1 将 LogUp 协议中的方程修改如下:
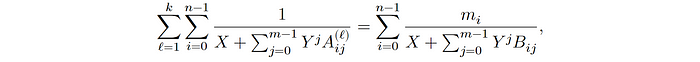
证明者必须承诺多重性,并承诺矩阵 A_{ij}^{(1)}, A_{ij}^{(2)}, … , A_{ij}^{(k)} 和 B_ij。
如果一个芯片只有本地或全局查找(包括“发送”和“接收”),则其排列轨迹的宽度为 (sends.len + receives.len)/2 + 1,这意味着两个查找用于计算一列排列轨迹,并额外增加一列用于累加和。
如果一个芯片既具有本地查找又具有全局查找,则其排列轨迹是上述步骤中计算得到的全局排列轨迹和局部排列轨迹的串联。具体计算排列轨迹的代码请参见: sp1/crates/stark/src/permutation.rs。
(7) 预处理轨迹
SP1 预处理轨迹是在生成 pk(证明密钥)和 vk(验证密钥)的设置阶段生成的,这意味着它不需要执行记录。除了 Program、Byte 和 MemoryProgram 芯片,其他芯片没有预处理轨迹。每个预处理轨迹都有其自己的轨迹列结构。
3. 预编译
椭圆曲线操作和哈希计算在以太坊生态系统中非常常见,但它们在 zkVM 中的计算成本通常很高,导致较长的证明生成时间。为了解决此问题,SP1 引入了预编译技术。
预编译集成到 SP1 zkVM 中以加速常见操作。在底层,预编译是通过专门设计用于证明一个或几个操作的自定义 STARK 表(轨迹)实现的。它们通常会以几个数量级提高 SP1 中昂贵操作的性能。例如,syscall_sha256_extend 在使用预编译时,仅需证明少量指令,而否则可能需要证明从 SHA-256 函数编译的数百或数千条 RISC-V 指令。
在 zkVM(可以视为一个操作系统)中,预编译被暴露为系统调用,并通过 RISC-V 指令 ecall 执行。每个预编译都有一个唯一的系统调用编号并实现一个特定计算的接口(execute 函数)。
以 syscall_sha256_extend 为例:
1) API 在 sp1/crates/zkvm/lib/src/lib.rs 中暴露。
extern "C" {
/// 使用给定的退出代码停止程序。
pub fn syscall_halt(exit_code: u8) -> !;
/// 将给定缓冲区中的字节写入给定的文件描述符。
pub fn syscall_write(fd: u32, write_buf: *const u8, nbytes: usize);
/// 从给定的文件描述符读取字节到给定缓冲区。
pub fn syscall_read(fd: u32, read_buf: *mut u8, nbytes: usize);
/// 在给定的字数组上执行 SHA-256 扩展操作。
pub fn syscall_sha256_extend(w: *mut [u32; 64]);
//…
}2) API 实现在 sp1/crates/zkvm/entrypoint/src/syscalls/sha_extend.rs。
##[allow(unused_variables)]
##[no_mangle]
pub extern "C" fn syscall_sha256_extend(w: *mut [u32; 64]) {
#[cfg(target_os = "zkvm")]
unsafe {
asm!(
"ecall",
in("t0") crate::syscalls::SHA_EXTEND,
in("a0") w,
in("a1") 0
);
}
#[cfg(not(target_os = "zkvm"))]
unreachable!()
}3)syscall_sha256_extend 在 zkVM 中被分配了一个唯一的系统调用编号:crate::syscalls::SHA_EXTEND。其具体计算代码位于文件 sp1/crates/core/executor/src/syscalls/precompiles/sha256/extend.rs 中:
pub(crate) struct Sha256ExtendSyscall;
impl Syscall for Sha256ExtendSyscall {
fn num_extra_cycles(&self) -> u32 {
48
}
fn execute(
&self,
rt: &mut SyscallContext,
syscall_code: SyscallCode,
arg1: u32,
arg2: u32,
) -> Option<u32> {
let clk_init = rt.clk;
let w_ptr = arg1;
assert!(arg2 == 0, "arg2 必须为 0");
//…
// 推送 SHA 扩展事件。
let lookup_id = rt.syscall_lookup_id;
let shard = rt.current_shard();
let event = PrecompileEvent::ShaExtend(ShaExtendEvent {
lookup_id,
shard,
clk: clk_init,
w_ptr: w_ptr_init,
w_i_minus_15_reads,
w_i_minus_2_reads,
w_i_minus_16_reads,
w_i_minus_7_reads,
w_i_writes,
local_mem_access: rt.postprocess(),
});
let syscall_event =
rt.rt.syscall_event(clk_init, syscall_code.syscall_id(), arg1, arg2, lookup_id);
rt.add_precompile_event(syscall_code, syscall_event, event);
None
}
}4)事件与芯片
每个预编译都有一个事件和一个相应的 Chip。对于 sha256_extend,它们分别定义如下。
ShaExtendEvent: sp1/crates/core/executor/src/events/precompiles/sha256_extend.rs
ShaExtendChip: sp1/crates/core/machine/src/syscall/precompiles/sha256/extend/air.rs
5)何时由 zkVM 执行 syscall_sha256_extend?
当 zkVM 在 execute_instruction()(sp1/crates/core/executor/src/executor.rs)中执行客户程序指令时,如果它遇到系统调用指令 Opcode::ECALL,则进入预编译处理。
fn execute_instruction(&mut self, instruction: &Instruction) -> Result<(), ExecutionError> {
//…
// 系统指令。
Opcode::ECALL => {
// 我们查看寄存器 x5 以获取系统调用 ID。我们不直接 `self.rr` 这个
// 寄存器的原因是我们稍后会写入它。
let t0 = Register::X5;
let syscall_id = self.register(t0);
c = self.rr(Register::X11, MemoryAccessPosition::C);
b = self.rr(Register::X10, MemoryAccessPosition::B);
let syscall = SyscallCode::from_u32(syscall_id);
//…
let syscall_impl = self.get_syscall(syscall).cloned();
//...
// 执行特定计算,例如上述提到的 SHA_EXTEND 的 execute() 函数。
let res = syscall_impl.execute(&mut precompile_rt, syscall, b, c);//
//...
}为方便客户程序使用预编译,SP1 修补了 RISC-V 上的椭圆曲线函数和哈希算法库,具体请参见 https://github.com/sp1-patches/ 。
4. 商多项式
SP1 中商多项式的构造与 p3/uni-stark/ 中的实现略有不同,原因是 SP1 的自定义 ProverConstraintFolder 约束。商的计算在 sp1/crates/stark/src/quotient.rs 中实现。
4.1 定义
商多项式是在 STARK 中的核心概念,用于验证目标多项式 P(x) 是否满足特定约束条件。其公式为:

其中:
- α:一种 Fiat-Shamir 随机组合因子(从 Challenger 处采样),用于线性组合多个约束。
- Z_H (x):域 H 上的 消失多项式。
- C_i(x):由 P(x) 上的约束条件导出的多项式。这些约束是在
eval()函数中通过assert_zero、assert_eq或其他assert_xx调用生成的。这些约束多项式的累积在sp1/crates/stark/src/folder.rs中计算。
fn assert_zero<I: Into<Self::Expr>>(&mut self, x: I) {
let x: PackedVal<SC> = x.into();
self.accumulator *= PackedChallenge::<SC>::from_f(self.alpha);
self.accumulator += x;
}
fn assert_zero_ext<I>(&mut self, x: I)
where
I: Into<Self::ExprEF>,
{
let x: PackedChallenge<SC> = x.into();
self.accumulator *= PackedChallenge::<SC>::from_f(self.alpha);
self.accumulator += x;
}4.2 目的
如果多项式 P(x) 满足约束,则约束多项式
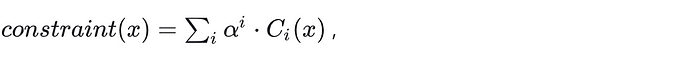
应在 H 中的所有点上都计算为零。因此,Constraints(x) 必须能被 Z_H (x) 整除,得到商多项式 q(x)。
验证者检查 q(x) 是否为 低度多项式 以验证 P(x) 是否满足约束。
4.3 消失多项式 Z_H (x)
消失多项式 Z_H (x) 确保约束多项式 Constraints(x) 在域 H 中的所有点都计算为零。它定义为:
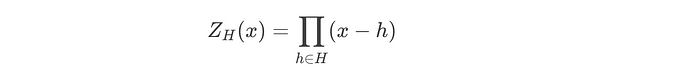
4.4 示例约束多项式构造
为简单起见,我们使用来自 plonky3/uni-stark/tests/fib_air.rs 的 Fibonacci 示例(尽管 SP1 的芯片约束更复杂)。eval() 函数包含 5 个 assert_xxx 约束,生成 5 个约束多项式:
impl<AB: AirBuilderWithPublicValues> Air<AB> for FibonacciAir {
fn eval(&self, builder: &mut AB) {
let main = builder.main();
let pis = builder.public_values();
let a = pis[0];
let b = pis[1];
let x = pis[2];
let (local, next) = (main.row_slice(0), main.row_slice(1));
let local: &FibonacciRow<AB::Var> = (*local).borrow();
let next: &FibonacciRow<AB::Var> = (*next).borrow();
let mut when_first_row = builder.when_first_row();
when_first_row.assert_eq(local.left, a); //C_1(x)
when_first_row.assert_eq(local.right, b); //C_2(x)
let mut when_transition = builder.when_transition();
// a' <- b
when_transition.assert_eq(local.right, next.left); //C_3(x)
// b' <- a + b
when_transition.assert_eq(local.left + local.right, next.right); //C_4(x)
builder.when_last_row().assert_eq(local.right, x); //C_5(x)
}
}1)第一行约束
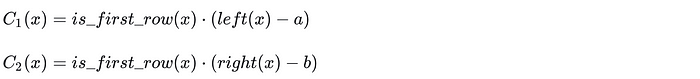
2)过渡约束
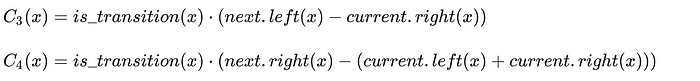
3)最后一行约束

注意:使用 coset LDE,is_first_row() 不仅仅适用于 LDE 扩展轨迹的第一行。类似地,is_transition() 和 is_last_row() 也不仅限于中间行或最后一行。相反,它们的约束分布在所有行中。
5. 参考文献
1) SP1 技术白皮书, https://drive.google.com/file/d/1aTCELr2b2Kc1NS-wZ0YYLKdw1Y2HcLTr/view
2) https://learnblockchain.cn/article/19265/
3) Ulrich Hab ̈ock 和 Al Kindi。关于向 STARKs 添加零知识的说明。2024 年 4 月, https://eprint.iacr.org/2024/1037.pdf
4) Starkware101。 https://starkware.co/wp-content/uploads/2021/12/STARK101-Part2.pdf
5) Ulrich Hab ̈ock。关于 FRI 低度测试的总结。IACR 预印本档案 2022/1216,2022 年。 https://eprint.iacr. org/2022/1216
6) Coset。 https://github.com/coset-io/zkp-academy/tree/main/FRI%26Stark
7) Trapdoor-Tech。https://trapdoortech.medium.com/zero-knowledge-proof-introduction-to-sp1-zkvm-source-code-d26f88f90ce4
8) StarkWare 团队。ethSTARK 文档 - 版本 1.2。在 IACR 预印本档案 2021/582,2023 年。 https://eprint.iacr.org/2021/582
9) Plonky2。 https://github.com/0xPolygonZero/plonky2
10) Plonky3。 https://github.com/Plonky3/Plonky3
11) Succinct labs。 https://github.com/succinctlabs/sp1
12) Justin Thaler。证明、论据和零知识。2022 年 12 月。
13) Vbuterin。快速的重心插值教程。 https://hackmd.io/@vbuterin/barycentric_evaluation
- 原文链接: medium.com/@gavin.ygy/ma...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,在这里修改,还请包涵~
- Vitalik: 重新评估以太坊 Layer2 448 浏览
- lambdaworks 2026 年更新路线图和优先级 421 浏览
- 基于递归STARK的带宽高效内存池 - 网络 101 浏览
- 从零开始构建 ZK (STARK) 证明器的旅程 975 浏览
- 零知识证据,给 Cashu 带来任意的花费条件 805 浏览
- ZK/SEC季度报告 689 浏览
- ZK/SEC 季度报告 626 浏览
- Succinct Labs:SP1和SPN有什么区别? 1719 浏览
- Circle STARKs:第三部分,Circle FFT - ZKSecurity 2406 浏览
- ZKsync Airbender:最快的开源 RISC-V zkVM 2110 浏览
- 基于格的签名聚合 1082 浏览
- zkVerify:模块化时代缺失的一层 909 浏览

