pm-AMM：一种用于预测市场的统一自动做市商

markdown 大纲

• 1. 引言
• 2. 贡献
• 3. 背景
  • 1. 预测市场
  • 2. 损失与再平衡和均匀性
• 4. 相关工作
• 5. 模型
• 6. 均匀 AMM
• 7. 静态 pm-AMM
• 8. 动态 pm-AMM
• 9. 结论
• 10. 致谢

引言

在这篇文章中，我们提出了一种针对预测市场的新型自动化市场制造商（AMM）：pm-AMM。

AMM 及其前身，如市场评分规则，最初被发明用于为预测市场提供流动性。它们现在主导了大多数加密货币的去中心化交易量。

但具有讽刺意味的是，尽管预测市场的交易量在加密领域激增，大多数都使用订单簿，而不是 AMM。

一个可能的原因是，现有的自动化市场制造商与结果代币（如果事件发生，则解析为 $1；如果未发生，则为 $0 的代币）不太匹配。结果代币的波动性依赖于事件的当前概率和预测市场到期的时间，这意味着池提供了一致性较差的流动性。流动性提供者 (LP) 一旦预测市场到期，实际上也基本上保证会失去全部价值。

我们提出了一种围绕这些考虑进行优化的新 AMM。这需要解决一个长期以来的 AMM 研究问题：AMM 进行特定类型资产的优化意味着什么？换句话说，给定某种资产的模型（例如期权、债券、稳定币或结果代币），这应如何影响我们为其使用的 AMM？我们基于损失与再平衡（LVR）这一概念提出了对此问题的可能解答。

贡献

我们为某些结果代币的价格过程开发了一个模型，我们称之为 高斯评分动态。该模型可能适合于预测某一潜在随机游走（例如篮球比赛的得分差距、选举中的投票差距或某项资产的价格）在未来某个到期时是否高于某个值的预测市场。

我们使用这个模型推导出了一种新的基于不变的 AMM 适用于这些代币，称为 静态 pm-AMM 不变式：

$$(y−x)Φ(y−xL)+Lϕ(y−xL)−y=0,$$
$$(y - x) \Phi\left( \frac{y - x}{L} \right) + L \phi\left( \frac{y - x}{L} \right) - y = 0,$$
其中

$$x$$ 是 AMM 的一种结果代币的储备，
$$y$$ 是其对面、互补结果代币的储备，
$$L$$ 是一个整体流动性或缩放因子，
$$ϕ$$ 和 $$Φ$$ 分别是正态分布的概率密度函数和累积分布函数。

要推导这个，我们利用了 损失与再平衡（LVR）这一强大概念，可以被视为 AMM 由于套利而损失金钱的速率。损失与再平衡不仅取决于 AMM 的形状，还取决于在其上交易的基础资产的价格过程。

我们为某种资产定义一个 均匀 AMM，即如果用于该资产，其 LVR 与某一时刻的投资组合价值成正比，而与当前价格无关。Milionis 等 确立了对于遵循几何布朗运动（普通资产如股票和加密货币的价格过程的一个流行模型）的资产，恒定几何均值市场制造商（如 Uniswap 和 Balancer）是唯一的均匀 AMM。静态 pm-AMM 是一种均匀 AMM，适用于根据我们的高斯评分动态模型表现的结果代币。

尽管静态 pm-AMM 对于所有价格具有均匀的 LVR（作为投资组合价值的比例），LVR 仍会在预测市场到期时逐渐增加。这是因为预测市场在到期前可能非常波动。我们展示了如何调整 pm-AMM 以减少其流动性，使得 AMM 在剩余的到期时间内的预期 LVR 在所有时刻保持不变。这给我们带来了 动态 pm-AMM 不变式，依赖于到期时间 (T−t):

$$(y−x)Φ(y−xL(T−t))+L(T−t)ϕ(y−xL(T−t))−y=0.$$
$$(y - x) \Phi\left( \frac{y - x}{L\sqrt{T - t}} \right) + L\sqrt{T - t} \phi\left( \frac{y - x}{L\sqrt{T-t}} \right) - y = 0.$$

动态 pm-AMM 并不是魔法——它通过提供逐渐减少的流动性来防止 LVR 在到期临近时增加。这在真实池中不一定是可取的，特别是因为非套利交易活动（因此费用）可能会随着时间的推移而增加。但 pm-AMM 为流动性提供者基于预期费用和他们想要分配的套利暴露，调整其流动性提供了框架。

这些 AMM 可能对在链上预测市场启动被动流动性很有用。均匀 AMM 的概念及其寻找方法，也可能在希望为其他行为不遵循几何布朗运动的资产定制 AMM 的去中心化交易设计者中更广泛适用，例如稳定币、债券、期权或其他衍生品。

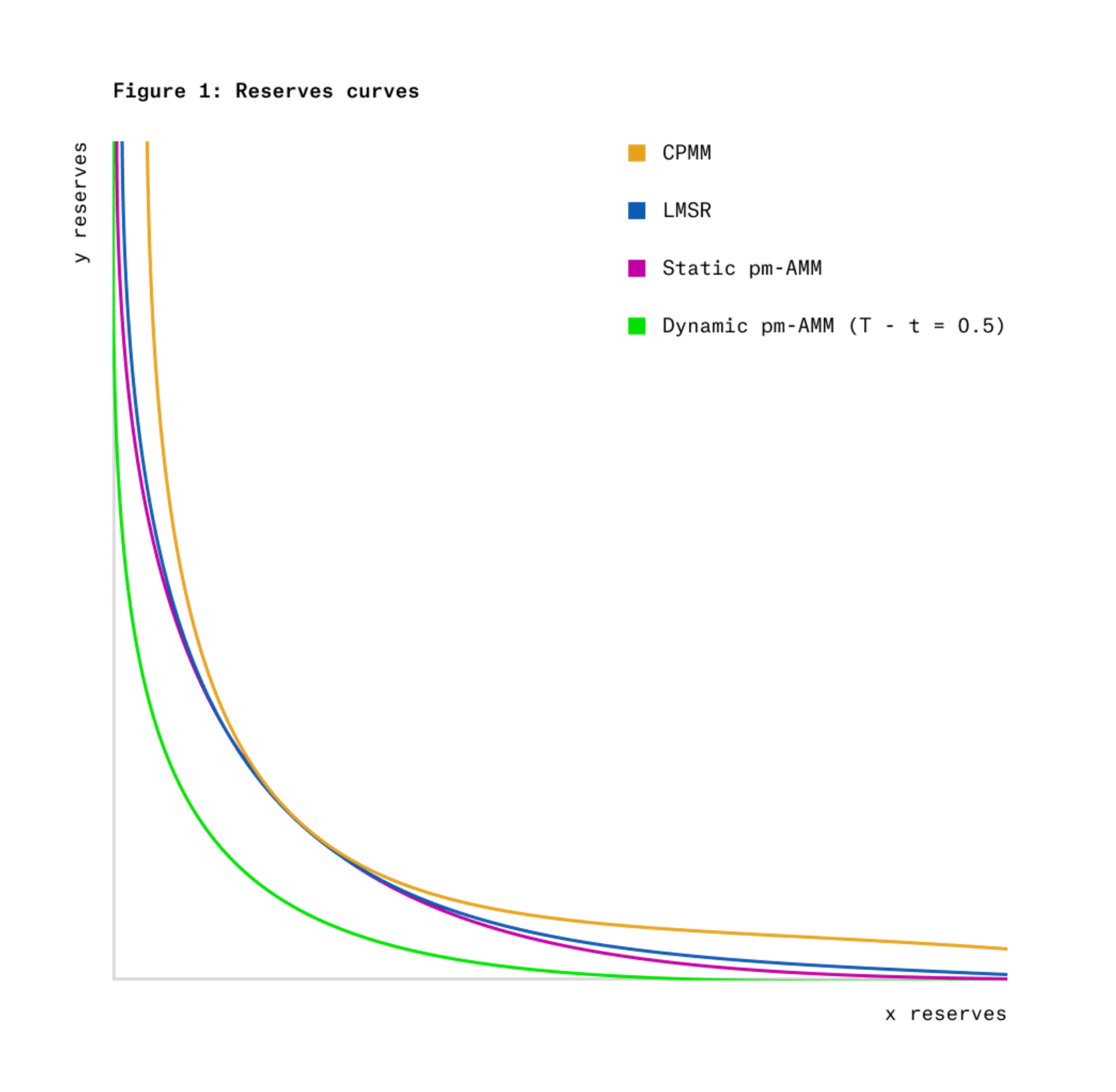
图 1 显示了静态和动态 pm-AMM 的不变曲线，与其他知名不变曲线进行比较，即恒定乘积市场制造商 (CPMM) 和对数市场评分规则 (LMSR)。请注意，动态 pm-AMM 的储备曲线随着时间提供的流动性较少。

图 2 显示了静态 pm-AMM 的 流动性指纹，显示如果不变式在 Uniswap v3 集中流动性 AMM 上实现，那么它会是什么样子，与 CPMM 和 LMSR 相比。水平轴对应于相对价格的刻度（代币 $$x$$ 的价格除以代币 $$y$$ 的价格），为对数刻度，垂直轴则对应于每个 AMM 在该价格水平提供的流动性。请注意，与两个替代方案相比，pm-AMM 在相对价格为 1（概率为 50%，即两种代币价格相等时为 0.50）附近集中更多流动性，并在极端相对价格（无论是非常低还是非常高）提供较少的流动性。

背景

预测市场

预测市场在加密领域越来越受欢迎。Polymarket 在 2024 年 10 月仅一个月内的交易量超过 20 亿美元。

然而，尽管 AMM 在其他大多数去中心化交易量中占主导地位，但目前大多数加密预测市场流动性都存在于订单簿中，而不是 AMM 中。

一个可能的原因是结果代币的行为与普通资产不同，因此为它们设计的 AMM 的效果并不一致。

例如，假设有一个关于比赛结果的预测市场，在这个比赛中，有人抛掷 1,001 次Coin。对应每个结果，这个游戏有两个代币：

代币 $$x$$ 如果正面朝上比反面朝上的多，则解析为 $1；如果反面朝上的多，则解析为 $0；对于代币 $$y$$ 也是如此，反之亦然。

这些结果代币的波动性高度依赖于剩余翻转次数和当前得分。当前得分越接近平均，剩余的翻转越少，这些代币的波动性就越高。这意味着常数乘积市场制造商的损失（如下面讨论的那样与波动性相关）会随时间而经历巨大的变化。

图 3 显示了在高斯评分动态下结果代币价格过程的波动性——事件是否高于零的决定是由某个随机游走最终的结果决定的——作为代币价格和剩余时间的函数。

许多流行的预测市场可以大致被视为类似于这个抛Coin的例子——对某些随机游走在未来某个过期时是否高于或低于 0 进行预测的赌注。例如：

• 对一场实时篮球比赛结果的预测市场，一旦剩余的比赛时间达到 0 就到期。在这个例子中，随机游走是两个球队之间的得分差。
• 关于总统选举结果的预测市场，直到选举日到期。在这个例子中，随机游走可以被视为打算投票给候选人的选民人数之间的差异。
• 预测某项资产（如比特币）在未来日期的价格是否高于某个行权价格的预测市场。在这个例子中，随机游走可以是当前比特币价格的对数减去某个行权价格。

在这篇文章中，我们定义了结果代币的价格演变模型——高斯评分动态模型，灵感来自上述示例。该模型假设预测市场价格与某种基础布朗运动在 0 以上结束的概率相匹配。

该模型类似于用于二元期权的 Black-Scholes 模型（如果某资产的价格超过某个行权点，它将支付固定的美元金额，否则为 $0 的工具）。但是在我们的模型中，基础过程不要求对应于可交易资产的价格。

我们确实做了简化假设，认为结果代币的价格与其解析为 $1 的概率相匹配。这省略了市场的重要特征，包括风险和时间偏好——如何影响该模型的研究是未来的课题。

我们还应该指出，并非所有预测市场都适合高斯评分动态模型，这假设新信息出现的速率是可预测的。例如，篮球比赛的适合度可能比足球比赛好，因为得分更加频繁，所以得分差异的演变随时间的变化更一致。一些类型的预测市场根本不会类似于本模型，例如对能否在某个特定日期之前发生某种一次性突发事件（如地震）的预测市场。但是该模型可能是推导其他动态模型的有用起点，并能作为推导任何模型的均匀 AMM 方法论的演示。

损失与再平衡和均匀性

在规定该模型后，我们推导出了一种可能更好地优化这些代币的自动市场制造商，优于现有的 AMM，如常数乘积市场制造商或 LMSR。我们用作指南的度量是流动性提供者的预期损失速率，最佳可描述为“损失与再平衡”，即 LVR。

LVR 捕捉了 AMM 的主要逆向选择成本：在没有交易的情况下，AMM 上的价格是静态的，随着新信息的公布而变得过时。LVR 捕捉了因这些过时价格被更有信息优势的套利者利用，从而使其在不利价格下进行交易而使 AMM 流动性提供者遭受的成本。因此，LVR 可以看作是 AMM 为了使其价格得到纠正而向套利者支付的金额。

此外，在没有交易费用的情况下，LVR 也是流动性提供者通过单独持有与其在池中储备的代币相同数量的代币的空头头寸所产生的损失。通过这种方式，LVR 建立了著名的 Black-Scholes 模型在期权定价中的主要洞见：正如期权通过与基础资产的 delta 对冲去除市场风险一样，LVR 衡量了在去除市场风险后流动性提供者在 AMM 中的头寸。这就是说，LVR 孤立了作为流动性提供者与简单持有 AMM 储备的相同代币的市场风险之间的区别。

我们考虑简单的基于不变的 AMM，没有费用或 MEV 回收机制。在这种情况下，AMM 是 '保证' 会因执行套利而亏损的——没有 AMM 不变可以消除 LVR（除了导致根本没有交易的一个）。甚至“最小化” LVR 在这里都是没有意义的：减少 LVR 只是意味着减少提供的流动性。

但我们可以使 LVR 更加一致，从而不依赖于资产当前价格的影响。我们称这种特性为 均匀性。

让均匀性变得有价值的一个方法是设想有一个赞助者愿意在某个零费用预测市场中提供流动性，以便了解市场对结果的预测。这意味着他们将会损失金钱，但自然希望将损失平均分配，而不是在特定时间或特定价格上集中损失。在此情况下，池的当前投资组合价值可以被视为赞助者的“预算”。在均匀 AMM 中，如果赞助者在某个时刻投入 1 美元的流动性，则他们在下一个时间步中的预期损失与池的当前状态无关。

但是对寻求利润的流动性提供者而言，均匀性也可能相关。即使 AMM 能够捕捉到其一些损失与再平衡，甚至获得利润（通过非零的交易费用，或通过拍卖机制如 MEV 税），它仍然需要一些策略来在不同价格和不同时期分配其流动性。我们可以将零费用池的预期损失视为获取某个时刻策略在流动性中的分配量的一种方式，这种方式考虑了资产的价格过程。

我们为特定资产定义 均匀 AMM 为：其预期 LVR 是池当前价值的常数比例，而与资产当前价格无关。

请注意，AMM 是否具有均匀 LVR 取决于资产自身的价格过程。如 Milionis 等 附录 B.2 所示，如果资产的价格遵循几何布朗运动，那么该资产与基准物之间唯一的均匀 AMM 是权重几何均值市场制造商，其不变量为 $$x^{\theta}y^{1 - \theta} = L$$，其中 $$\theta \in (0,1)$$。这是在 Balancer 中使用的公式，而 Uniswap v2 中使用的常数乘积市场制造商是其一个特例。

但是，对于遵循高斯评分动态的代币，常量几何均值 AMM 不具备均匀 LVR。而对数市场评分规则 (LMSR) 最初是为预测市场开发的 AMM，也没有均匀 LVR。

图 4 显示了 CPMM 和 LMSR 在用于时间 $$T−t=1$$ 的高斯评分动态结果代币时的 LVR，相比 static pm-AMM 的均匀 LVR：

出于这些考虑，我们开发了两种 AMM，旨在针对在高斯评分动态下的预测市场——一种在任意给定时间具有均匀 LVR，但随着预测市场到期逐渐增加 LVR，另一种在剩余时间范围内具备均匀 LVR 及恒定预期 LVR。

如图 4 所示，当结果代币价格处于极端（接近零或一）时，CPMM 和 LMSR 经历了较大 LVR（作为池价值的比例）。这是因为，尽管在这些点附近的价格波动性较低（参见图 3），池的价值在极端价格下衰减得更快。因此，均匀 AMM 应在极端价格下提供较少的流动性，而这正是 pm-AMM 设计所做的（参见图 2）。

相关工作

AMM 起源于预测市场和市场评分规则的世界，例如 对数市场评分规则 (LMSR)。这些规则激励了常量函数市场制造商 (CFMM) 的发现，如 Uniswap v2，其通常由 AMM 各种资产储备之间的不变量关系特征。基于这种设计的 AMM 近年来已成为区块链上去中心化交易的主导市场机制。

最近，金融经济学的理念被应用于理解自动化市场制造的成本，以损失与再平衡的形式，即 LVR，如 Milionis 等 讨论的那样。LVR 捕捉了因过时价格而给 AMM 带来的套利者所产生的损失。那篇论文考虑了遵循扩散过程的资产，主要集中在几何布朗运动上。

另一方面，由于其有界回报和有限的时间范围，预测市场则具有非常不同的价格动态。Taleb 提出了基于基础可观察选举过程的动态，而我们开发了一种基于基础可观察高斯评分过程的替代动态形式。

先前也有一些关于为非 GBM 资产设计自动市场制造商的应用工作。例如， StableSwap 是为稳定币对设计的 AMM，该设计基于直观前提出发，即在相关且均值回归的资产之间的 AMM 应集中流动性靠近单一价格，但其推导并不涉及对资产价格过程的建模。另一个是 YieldSpace，这是为零息债券设计的 AMM。尽管 YieldSpace 的推导确实涉及了将零息债券的价格建模为利率函数的简单模型，但它没有包括价格过程的完整模型（因为它并不建模利率的演变），并且该论文对如何从当前储备推断利率进行了大致笔画的选择。

还有一些学术工作围绕着基于对资产价格行为的信念来设计 AMM。例如 Goyal 等。他们的框架旨在最大化预期活跃流动性的数量，而不是使预期损失均匀化，因此有时得出与我们的相反的影响。例如，他们的论文表明，LMSR （与 CPMM 相比，其流动性集中在价格 1 附近）的适配良好，若流动性提供者预期相对资产价格将保持在 1 附近，而我们的框架表明，如果你预期价格会偏离（结果代币的表现），则有理由集中流动性于 1 附近。

模型

自动化市场制造。我们考虑一个关于单一事件的预测市场，以及一个交易相互抵消的两个资产的 AMM：一种高风险资产（记为 $$x$$），如果事件发生，则支付一美元，否则不支付；另一种高风险资产（记为 $$y$$）则支付相反款项。AMM 维持一个不变量：

$$f(x,y)=L$$，其中 $$f(⋅,⋅)$$ 是储备 $$(x,y)$$ 的不变量函数，而 $$L$$ 是一个常数。给定资产 $$x$$ 的价格 $$P$$，定义 池值函数 为：

$$V(P)≜\min{(x,y) \in \mathbb{R}{+}^2} P x + (1 - P) y \ \text{subject \ to} \ f(x,y)=L.$$
(1)

这是在资产 $$x$$ 价格为 $$P$$ 时的池值。由于持有一单位的 $$x$$ 和 $$y$$ 资产相当于持有现金，因此我们必须有 $$y$$ 资产的价格为 $$1-P$$。

我们假设存在一群套利者，他们在每个时间 $$t$$ 都可以观察到资产 $$x$$ 的价格 $$P_t$$（也观察到资产 $$y$$ 的价格 $$1-P_t$$）。假设没有交易费用或其他摩擦，这些套利者会持续监控 AMM，并寻找从任何错误定价中提取价值。当最大化自身利润时，他们会以最小化 AMM 储备的价值的方式进行交易。如果我们将 $$V_t$$ 表示为在时间 $$t$$（当价格为 $$P_t$$）的储备值，那么我们必须有 $$V_t=V(P_t)$$。

示例 1（常数乘积市场制造商）。在常数乘积市场制造商 (CPMM) 的情况下，其中不变量函数为：

$$f(x,y)≜\sqrt{xy}$$，池值函数为：

$$V(P)=2L \sqrt{ P(1-P)}.$$

示例 2（对数市场评分规则）。由 Robin Hanson 创建的 对数市场评分规则（LMSR）可以被视为满足不变量：

$$f(x,y)≜2^{-x/L} + 2^{-y/L} = 1$$，在这种情况下池值函数为：

$$V(P) = -L \left{ P \log_2 P + (1 - P) \log_2 (1 - P) \right}，$$

这与由价格隐含的事件的二元熵成正比。

令 $$x^(P)$$ 和 $$y^(P)$$ 为优化问题 (1) 的最优解，我们假设这些解存在、唯一，并且是价格 $$P$$ 的平滑函数。以下内容与 Milionis 等 的引理 1 类似，但适应了现在的背景：

引理 1。对于所有价格 $$P≥0$$，池值函数满足：

1.
$$V'(P)=x^(P)-y^(P).$$

2.
$$V''(P) = x^{ \prime}(P) - y^{ \prime}(P) \leq 0.$$

高斯评分动态。我们现在描述高风险资产价格如何在我们所称的 高斯评分动态 下随时间演变。特别地，我们假设在时间区间 $$t \in [0,T]$$ 内有一个随机过程 $${Z_t}$$，其中事件由在时间戳为 $$T$$ 时 $$Z_T$$ 的符号决定：如果 $$Z_T \geq 0$$，则资产 $$x$$ 有回报；反之如果 $$Z_T < 0$$，则资产 $$y$$ 有回报。我们可以将 $$Z_t$$ 理解为在双边竞争中两队之间的得分差异。因此，我们称 $$Z_t$$ 为得分过程。请注意，尽管我们的模型假设存在这个得分过程，但得分过程不需要被 AMM 直接观察。如下所述，AMM 可以通过边际价格（在被套利后）和到期时间推断当前得分的值。

我们假设 $$Z_t$$ 遵循随机游走。具体而言，我们假设 $$Z_t$$ 是一个具有方差 $$σ>0$$ 的布朗运动，即：

$$dZ_t=σ dB_t.$$

其中 $$B_t$$ 是标准布朗运动。因此，可以很容易看出，在时间 $$t$$ 时资产 $$x$$ 的价格 $$P_t$$ 必须给出：

$$Pt=E[I{Z_T>0}|Z_t]=Φ\left(\frac{Z_t}{σ\sqrt{T-t}}\right)$$，
$$Pt = \mathbb{E}\left[I{{Z_T> 0}} \ \big| \ Z_t \right] = \Phi\left(\frac{Z_t}{\sigma \sqrt{T-t}}\right)，$$

其中 $$Φ(⋅)$$ 是标准正态累积分布函数（CDF）。应用伊藤引理，
$$P_t$$ 必须满足：

$$dP_t=ϕ\left(\frac{Z_t}{σ\sqrt{T-t}}\right)dZ_t\sqrt{T-t}=ϕ\left(Φ^{-1}(P_t)\right)\frac{dB_t}{√{T-t}}.$$

$$dP_t = \phi\left(\frac{Z_t}{\sigma\sqrt{T-t}}\right) \frac{dZ_t}{\sigma\sqrt{T-t}}
= \frac{\phi\left(Φ^{-1}(P_t)\right)}{\sqrt{T-t}} dB_t，$$

其中 $$ϕ(⋅)$$ 是标准正态概率密度函数，而 $$Φ^{-1}(⋅)$$ 是反累积分布函数。请注意，尽管得分动态，以及得分到价格或相反的转换依赖于 $$σ$$，但价格过程 $$P_t$$ 的动态随孤立变化与 $$σ$$ 无关。这些动态的波动性，作为价格和剩余时间的函数，可参见图 3。

均匀 AMMs

损失与再平衡。从上述讨论中，如果我们用 $$V_t$$ 表示在时间 $$t$$ （当价格为 $$P_t$$）的储备值，那么我们必须有 $$V_t=V(P_t)$$。应用伊藤引理，我们得知池值随时间演变如下：

$$dV_t = \frac{1}{2} V''(P_t) (dP_t)^2 + V'(P_t) dP_t= \frac{1}{2}\phi\left(Φ^{-1}(P_t)\right)^2\frac{1}{T-t}V''(P_t)dt+(x^(P_t) - y^(P_t))dP_t.$$
(2)

由于价格 $$P_t$$ 是一个马尔可夫过程，(2) 的第二项也是马尔可夫过程，可能会增加或减少。然而，从 $$V(⋅)$$ 的凹性（参见引理 1）来看，第一项对应于负漂移，因此对应于一个减小的过程。这就是 Milionis 等 的损失与再平衡过程（LVR），并且它捕捉到池相对于在劣质价格进行交易而损失给套利者的价值。我们通过以下公式定义这种损失的瞬时率：

$$LVR_t≜- \frac{1}{2}\phi\left(Φ^{-1}(P_t)\right)^2\frac{1}{T-t}V''(P_t) \geq 0.$$
(3)

均匀 AMM。一种 均匀 AMM 是一种以与其价值成正比的恒定速率亏损池，即

$$LVR_t = \alpha V_t \quad（\text{其中} \alpha > 0） $$
LVR_t​=αVt​(其中α>0)

例如，Milionis 等 确立了对于遵循几何布朗运动的资产，实质上唯一的均匀 AMM 是几何均值市场制造商。在高斯评分动态下的预测市场中，检查 (3) 发现，均匀 LVR 池必须求解常微分方程：

$$-\frac{1}{2} \phi(Φ^{-1}(P))^{2}\frac{1}{T-t}V''(P) = \alpha V(P)$$。
这在这里并不可能，因为左侧依赖于 $$t$$，而右侧不依赖于 $$t$$。这里的核心问题是，与时间均匀的几何布朗运动不同，高斯评分动态高度依赖于时间。

为规避此问题，我们允许 $$α$$ 随时间改变，即我们设定 $$α = \frac{β}{T - t}$$，并现在考虑一个设置，在其中

$$LVR_t = \frac{β V_t}{T - t}$$。
$$LVR_t​=βT−t​Vt​$$

这等价于下面的常微分方程：

$$\phi(Φ^{-1}(P))^{2}V''(P) + 2βV(P) = 0, \quad(P \geq 0)$$
(4)

此外，驻留在 $$V(⋅)$$ 上的额外要求需满足有效池值函数，例如 $$V''(P) \leq 0$$（参见引理 1）。

静态 pm-AMM

池定义。上述 ODE 可以通过变量替换来简化：

$$u = Φ^{-1}(P)$$。

当 $$β=1/2$$ 时，有满足 ODE 及附加凹性条件的解，其由以下公式给出：

$$V(P) = L \phi(Φ^{-1}(P))，$$
$$V(P) = L \phi(Φ^{-1}(P))， $$

其储备由下列公式给出：

$$x^*(P) = L\left{ Φ^{-1}(P) P + \phi(Φ^{-1}(P)) - Φ^{-1}(P) \right}，$$
(5)

$$y^*(P) = L\left{ Φ^{-1}(P) P + \phi(Φ^{-1}(P)) \right}，$$
(6)

在这里，

是一个流动性参数，它决定了池大小的扩展。观察到 
y∗(P)−x∗(P)=LΦ−1(P)y^\*(P) - x^\*(P) = L \\Phi^{-1}(P)y∗(P)−x∗(P)=LΦ−1(P) 
并将其代入 (5)，池储备 
(x,y)(x,y)(x,y) 
必须满足不变性

(y−x)Φ(y−xL)+Lϕ(y−xL)−y=0。 (y - x) \\Phi\\left( \\frac{y - x}{L} \\right) + L \\phi\\left( \\frac{y - x}{L} \\right) - y = 0. (y−x)Φ(Ly−x​)+Lϕ(Ly−x​)−y=0。

这定义了**静态 pm-AMM**。 （这个名称暗示我们将很快讨论的 pm-AMM 的时间变化、动态变动。）通过设计，这个 AMM 满足关系

LVRt=Vt2(T−t)。\\mathsf{LVR}\_t = \\frac{V\_t}{2 (T - t)}. LVRt​=2(T−t)Vt​​。

定义

Vˉt=E\[Vt\]\\bar{V}\_t = \\mathbb{E}\[V\_t\] 
Vˉt​=E\[Vt​\]

作为预期池价值，从 (2) 我们得到

dVˉtdt=−Vˉt2(T−t)。\\frac{d\\bar{V}\_t}{dt} = - \\frac{\\bar{V}\_t}{2(T - t)}. 
dtdVˉt​​=−2(T−t)Vˉt​​。

解这个常微分方程，

Vˉt=V0T−tT。\\bar{V}\_t = V\_0 \\sqrt{\\frac{T-t}{T}}. 
Vˉt​=V0​TT−t​​。

换句话说，按预期，静态 pm-AMM 池的价值根据剩余时间的平方根衰减。

## 动态 pm-AMM

静态 pm-AMM 的一个缺点是，尽管它每一美元价值的 LVR 在所有可能的**价格**中是均匀的，但它随**时间**变化。特别是，每美元价值的损失与到期时间成反比，因此它将在到期前不断增加，直到失去所有价值。

**动态流动性**。现在我们想象一个动态的、时间变化的静态 pm-AMM 设计，在该设计中，AMM LPs 随着时间的推移撤回流动性以减轻他们的损失。特别是，假设池的价值由下列公式给出

V(P,t)=Ltϕ(Φ−1(P))，V(P,t) = L\_t \\phi\\left( \\Phi^{-1}(P) \\right)，V(P,t)=Lt​ϕ(Φ−1(P))， 

其中 

LtL\_tLt​ 

是一个确定性平滑函数，它决定了随着时间的推移移除（或可能添加）多少流动性。应用伊藤引理到池价值过程中 
Vt≜V(Pt,t)V\_t ≜ V(P\_t,t)Vt​≜V(Pt​,t) 
、

dVt=∂tV(Pt,t)+12∂PPV(Pt,t)(dPt)2+∂PV(Pt,t)dPt=(L˙tϕ(Φ−1(P))−Lt2(T−t)ϕ(Φ−1(P)))dt+(x∗(Pt)−y∗(Pt))dPt=(L˙tLt−12(T−t))Vtdt+(x∗(Pt)−y∗(Pt))dPt。（7） \begin{array}{ll} dV_t & = \partial_t V(P_t, t) + \tfrac{1}{2} \partial_{PP} V(P_t, t) \, (dP_t)^2 + \partial_P V(P_t, t) \, dP_t \\ & \displaystyle = \left( \dot{L}_t \phi\left( \Phi^{-1}(P) \right) - \frac{L_t}{2(T-t)} \phi\left( \Phi^{-1}(P) \right) \right) \, dt \\ & \quad + \big(x^{*}(P_t) - y^{*}(P_t) \big) \, dP_t \\ & \displaystyle = \left( \frac{\dot{L}_t}{L_t} - \frac{1}{2(T-t)} \right) V_t \, dt + \big(x^{*}(P_t) - y^{*}(P_t) \big) \, dP_t. \end{array} \quad\quad \tag{7}

记作 

CtC\_tCt​ 

为撤回的流动性累计美元价值。然后，由于池价值在线性与流动性 
LtL\_tLt​ 
，流动性变化的美元价值与 
Vt/LTV\_t/L\_TVt​/LT​ 
成正比。然后，我们有

dCt=−L˙tLtVtdt。dC_t = - \frac{\dot L_t}{L_t} V_t \, dt。 dCt​=−Lt​L˙t​​Vt​dt。

AMM LPs 的总财富 

WtW\_tWt​ 

t 包含池储备的价值加上撤回流动性的累计价值，因此 
Wt=Vt+CtW\_t = V\_t + C\_t 
Wt​=Vt​+Ct​，并满足

dWt=dVt+dCt=−12(T−t)Vtdt+(x∗(Pt)−y∗(Pt))dPt。dW_t = dV_t + dC_t = -\frac{1}{2(T-t)} V_t \, dt + \big(x^{*}(P_t) - y^{*}(P_t) \big) \, dP_t。 dWt​=dVt​+dCt​=−2(T−t)1​Vt​dt+(x∗(Pt​)−y∗(Pt​))dPt​。

这意味着预期 LP 财富

Wˉt≜E\[Wt\]\\bar{W}\_t ≜ \\mathbb{E}\[W\_t\] 
Wˉt​≜E\[Wt​\]

满足 

Wˉt=W0−∫0tVˉs2(T−s)ds,(8)\bar{W}_t = W_0 - \int_0^t \frac{\bar{V}_s}{2(T-s)} \, ds, \quad\quad \tag{8}

其中 

Vˉt≜E\[VT\]。\\bar{V}\_t ≜ {E}\[V\_T\]。Vˉt​≜E\[VT​\]。

**常数 LVR。** 现在，考虑流动性曲线的特定选择给定 

Lt=L0T−t。L\_t = L\_0 \\sqrt{T - t}. Lt​=L0​T−t​。

我们称之为动态 pm-AMM。然后，从 (7) ，预期池价值 

Vˉt=E\[Vt\]\\bar{V}\_t = E\[V\_t\] 
Vˉt​=E\[Vt​\]

满足 

dVˉtdt=(L˙tLt−12(T−t))Vˉt=−VˉtT−t。\frac{d \bar{V}_t}{dt} = \left( \frac{\dot{L}_t}{L_t} - \frac{1}{2(T-t)} \right) \bar{V}_t = - \frac{\bar{V}_t}{T - t}. dtdVˉt​​=(Lt​L˙t​​−2(T−t)1​)Vˉt​=−T−tVˉt​​。

解这个常微分方程，我们有 

Vˉt=V0T−tT。\\bar{V}\_t = V\_0 \\, \\frac{T-t}{T}. 
Vˉt​=V0​TT−t​。

换句话说，净撤回后，预期池价值在动态 pm-AMM 中线性减少。此外，因为它继承了静态 pm-AMM 的价值函数，每单位时间的 LVR 损失率为 

LVRt=12(T−t)Vt。\\mathsf{LVR}\_t = \\frac{1}{2(T-t)} V\_t. 
LVRt​=2(T−t)1​Vt​。

然后，预期损失率为 

E[LVRt]=12(T−t)Vˉt=V02T,\mathbb{E}[\mathsf{LVR}_t] = \frac{1}{2(T-t)} \bar{V}_t = \frac{V_0}{2T}, E[LVRt​]=2(T−t)1​Vˉt​=2TV0​​，

这是在

ttt

上是恒定的。也就是说，动态 pm-AMM 以恒定的费率（按预期）向套利者损失资金。

最后，沿着 (8) ，这导致预期财富过程

WˉT=W0−∫0TV02Tdt=W0−V02=W02，\bar{W}_T = W_0 - \int_0^T \frac{V_0}{2T} \, dt = W_0 - \frac{V_0}{2} = \frac{W_0}{2}, WˉT​=W0​−∫0T​2TV0​​dt=W0​−2V0​​=2W0​​，

因此到期时损失一半的初始财富。

结论

pm-AMM 可能对受动态驱动的预测市场有用，这些动态类似于高斯得分动态模型。

除此之外，我们的工作表明，均匀 AMM 可能为其他类型的资产导出，例如债券、期权和其他衍生品。

致谢

作者感谢 Benedict Brady、Leo Lau、Allan Niemerg、Storm Slivkoff、Shouqiao Wang、Dave White 和 Bill Zhang 的宝贵意见。

• 原文链接： paradigm.xyz/2024/11/pm-...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～