解读强健的重质押网络 - 连锁攻击与验证者安全性

概述

在这篇博客文章中，我们将拆解并回顾论文 Robust Restaking Networks 的关键见解和贡献。我们将探讨 Durvasula 和 Roughgarden 提出的创新模型和条件，旨在确保即使在潜在攻击的情况下，重质押网络仍能保持安全。从超额抵押的重要性到稳健安全的数学特征，我们将分解重质押网络中加密经济安全的复杂概念，并理解这项研究在区块链安全背景下的重要性。

论文引用

Robust Restaking Networks by Naveen Durvasula, and Tim Roughgarden, arXiv:2407.21785 [cs.GT] https://doi.org/10.48550/arXiv.2407.21785

定义与符号 - 关键概念

为了理解“Robust Restaking Networks”这篇论文，我们首先需要打下坚实的基础。这些定义和符号是理解论文的工具包。让我们逐一分解。

验证者与服务：网络的支柱

• 验证者 $V$：验证者是区块链的无名英雄——他们验证交易，维护网络完整性，并确保一切顺利运行。每个验证者 $v$ 质押一定数量的加密货币 $\sigma_v$（如以太坊中的 ETH）作为抵押。如果他们行为不端，他们可能会失去这部分质押，这就是为什么它很重要。

• 服务 $S$：这些是验证者支持的任务或应用。可以将服务视为验证者可以承担的不同工作——从运行核心共识协议到确保数据可用性。每个服务 $s$ 都有一个腐败利润 $\pi_s$，这基本上是攻击者通过破坏它可能获得的赏金。

重质押图：映射网络

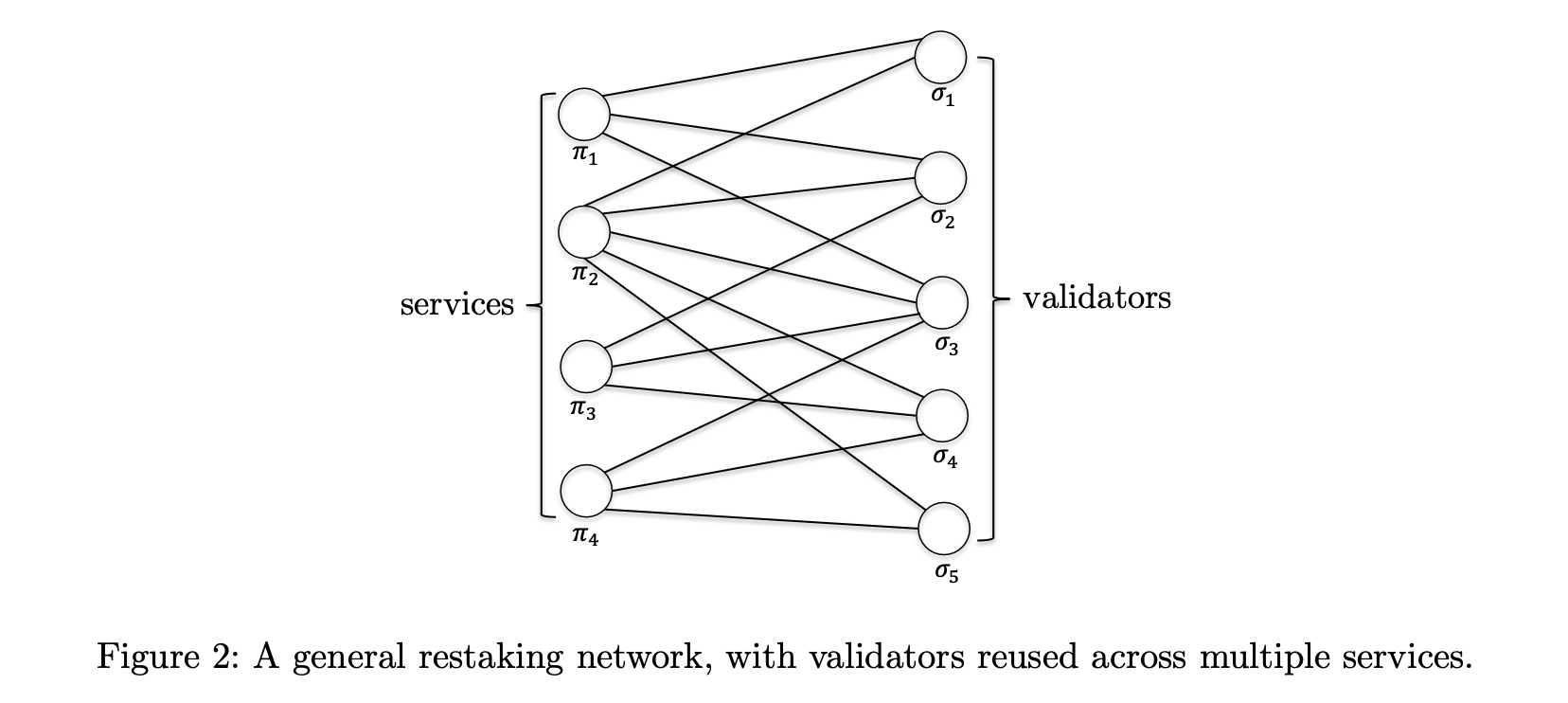
• 重质押图 $G$：想象一下网络的映射图，验证者和服务是地标。重质押图 $G = (S, V, E, \pi, \sigma, \alpha)$ 连接这些地标：

  • $S$：服务。
  • $V$：验证者。
  • $E$：显示哪些验证者支持哪些服务的边。
  • $\pi_s$：破坏服务 $s$ 的潜在利润。
  • $\sigma_v$：每个验证者 $v$ 的质押。
  • $\alpha_s$：破坏服务 $s$ 所需的总质押比例。

• 邻居 $N_G(A)$：在这个图中的邻居是直接连接。如果你在看一个服务 $s$，$N_G(s)$ 告诉你哪些验证者在支持它。如果你关注验证者，$N_G(v)$ 显示他们支持的服务。

攻击动态：验证者与服务的冲突

• 攻击联盟 $(A, B)$：当验证者决定联合起来并变得不诚实，他们形成一个攻击联盟。以下是其含义：

  • $A$：被攻击的服务集合。

  • $B$：执行攻击的验证者。

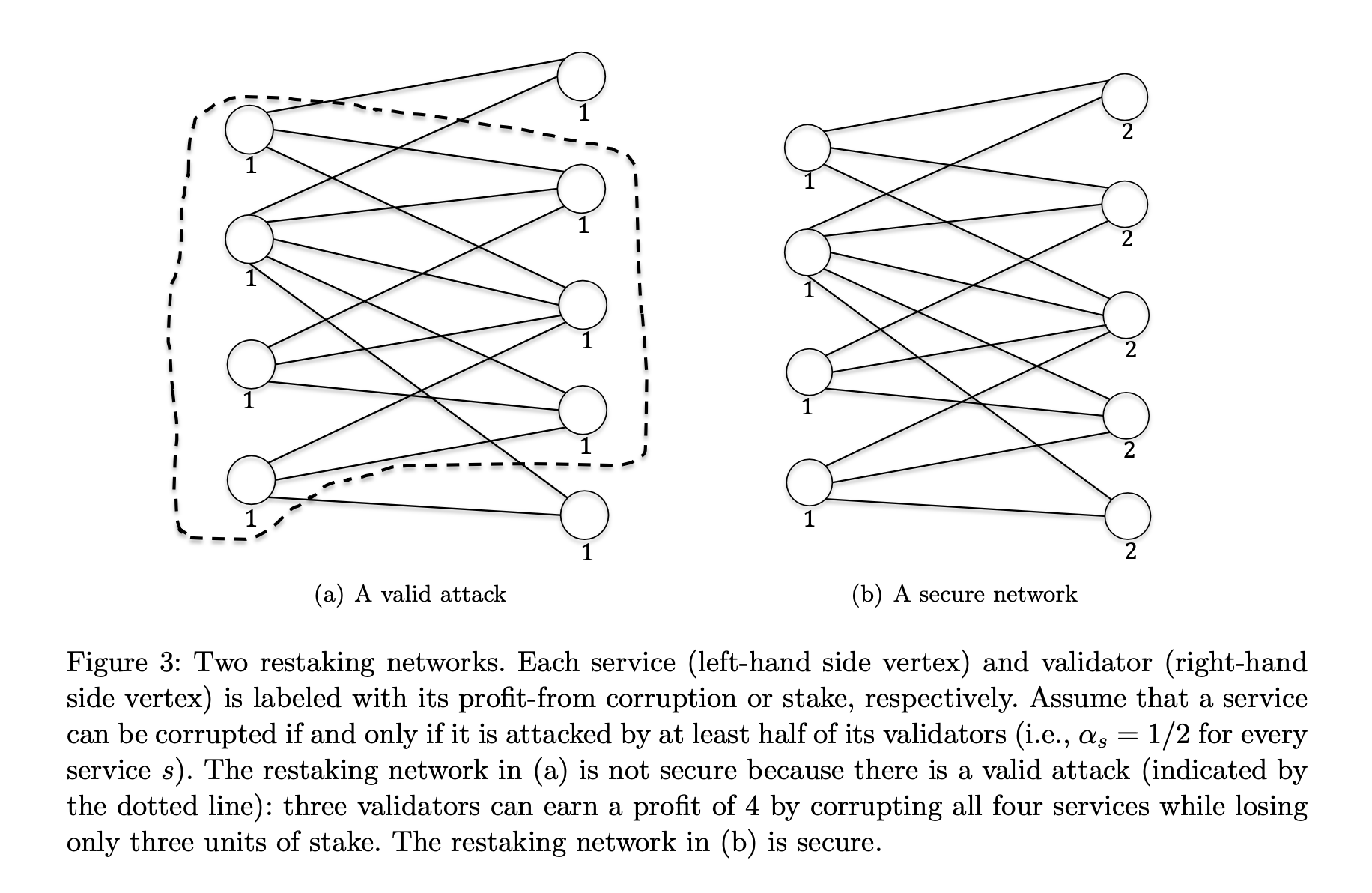
  • 如果满足以下条件，这个联盟是有效的：

  • 验证者 $B$ 控制足够的质押以压倒服务 $A$：

    $\sum_{v \in B \cap N_G(s)} \sigma_v \geq \alphas \sum{v \in N_G(s)} \sigma_v \quad \forall s \in A$

  • 攻击 $A$ 的利润大于 $B$ 可能失去的总质押：

    $\sum_{s \in A} \pis > \sum{v \in B} \sigma_v$

• 有效攻击：这是一个满足两个条件的攻击：验证者有足够的力量，并且攻击在经济上是值得的。

攻击后的重质押图 $G \downarrow B$：后果

• 攻击后的图 $G \downarrow B$：攻击后，网络不再相同。$G \downarrow B$ 表示在验证者 $B$ 被罚没后网络的状态。它就像一张显示战斗后剩余部分的地图——一些验证者消失了，网络必须依靠剩余的验证者继续运行。

稳定攻击：保持稳固

• 稳定攻击：并非所有攻击都是稳定的——有些更像是转瞬即逝的机会。稳定攻击确保联盟 $B$ 中的每个验证者都在做出有意义的贡献。这不仅仅是拥有足够的质押；还要确保没有搭便车的行为。数学上，这通过以下方式强制执行： $\sum_{v \in B \setminus B'} \sigmav < \sum{s \in A \setminus A'} \pi_s$ 对于任何子集 $A' \subseteq A$ 和 $B' \subseteq B$。这保证了联盟 $B$ 中的每个验证者都是攻击成功所必需的，使联盟稳固且稳定。

级联攻击：当一次攻击不够时

• 级联攻击：想象一种情况，网络中的一个小攻击或问题不会仅仅停留在小范围内——它会增长并蔓延，导致更大的问题。这就是作者所说的级联攻击。

以下是它的工作原理：

• 初始火花：这一切都始于一个小攻击或冲击——可能是一些验证者（那些保持网络安全的人）由于某些问题（例如软件错误）失去了他们的质押。
• 连锁反应：这个初始问题削弱了网络，使得另一个更大的问题可能发生。因为网络现在稍微不那么安全，下一次攻击更容易发生。这个新的攻击进一步削弱了网络，为下一次攻击奠定了基础，依此类推。
• 级联攻击：我们称这一系列事件为级联攻击。序列中的每一步都使下一步更有可能发生，导致连锁反应，最终可能导致网络中的重大损失。

在技术术语中，如果你有一个重质押图 $G$，它映射了验证者如何连接到服务，级联攻击序列 $(A_1, B_1), (A_2, B_2), \dots, (A_T, B_T)$ 中的每一步在已经被前几步削弱的网络上是有效的。$(A_t, Bt) \text{ 在 } G \downarrow \bigcup{i=1}^{t-1} B_i \text{ 上是有效的}$

这里，$G \downarrow B$ 表示在一些验证者被罚没和移除后的网络。

最坏情况下的质押损失：为最坏情况做准备

• 最坏情况下的质押损失 $R_\psi(G)$：现在，让我们谈谈最坏情况下的质押损失。这个概念是为了理解如果发生级联攻击，可能发生的最坏情况。

以下是其思路：

• 从一个小冲击开始：假设发生了不好的事情——一小部分验证者失去了他们的质押。这是初始冲击，用 $\psi$ 表示。
• 探索所有可能性：然后我们查看所有可能成为这个初始冲击一部分的验证者群体。我们基本上是在问：最坏的情况下，哪些验证者可能首先被击中？
• 对网络的影响：一旦这些验证者出局，网络就会发生变化——它不再像以前那样强大。我们用符号 $G \downarrow D$ 表示在初始验证者群体 $D$ 被罚没或移除后的网络。
• 最坏情况下的损失：现在，我们计算最坏情况下的质押损失 $R_\psi(G)$。这是一种估计由于初始冲击引发的级联攻击可能导致的质押最大损失的方法。换句话说，我们试图预见如果一个坏事件引发了一系列更坏的事件，情况会变得多糟糕。

这个指标很重要，因为它帮助我们理解网络在面对一系列故障时可能有多脆弱，并且它是设计能够承受最坏情况的系统的关键工具。它的计算方式如下：

$R\psi(G) = \psi + \max{D \in D\psi(G)} \max{(A_1, B_1), \dots, (A_T, BT) \in C(G \downarrow D)} \frac{\sigma{\bigcup_{t=1}^{T} B_t}}{\sigma_V}$

这里，$\psi$ 是系统的初始冲击（一小部分质押损失），$\sigma{\bigcup{t=1}^{T} B_t}$ 是通过所有级联攻击损失的总质押。

EigenLayer 充分条件：安全检查

• EigenLayer 充分条件：为了确保网络安全，EigenLayer 团队开发了一组条件[^1]，作为快速安全检查。如果验证者 $v$ 满足以下条件，则认为它是安全的： $\sum_{s \in N_G(v)} \frac{\sigmav}{\sigma{N_G(s)}} \cdot \frac{\pi_s}{\alpha_s} \leq \sigma_v$ 如果网络中的所有验证者都满足这个条件，这意味着网络是安全的，不会受到任何潜在攻击。

让我们更详细地拆解这一点。这也是论文中的Claim 1。

论文中的 Claim 1 指出，如果对于每个验证者 $v \in V$，以下不等式成立，则重质押图 $G$ 是安全的：

$\sum_{s \in N_G(v)} \frac{\sigmav}{\sigma{N_G(s)}} \cdot \frac{\pi_s}{\alpha_s} \leq \sigma_v$

这个声明很重要，因为它提供了一个充分条件，确保重质押网络是安全的，意味着在给定条件下不存在有效攻击。让我们逐步分解这个声明以理解它。

分解不等式

Claim 1 中的不等式可以解释如下：

• 左侧：$\sum_{s \in N_G(v)} \frac{\sigmav}{\sigma{N_G(s)}} \cdot \frac{\pi_s}{\alpha_s}$

  • $\sigma_{N_G(s)}$ 是所有支持服务 $s$ 的验证者的总质押。
  • $\frac{\sigmav}{\sigma{N_G(s)}}$ 表示验证者 $v$ 对服务 $s$ 的总质押的贡献比例。
  • $\frac{\pi_s}{\alpha_s}$ 是攻击服务 $s$ 的“成本效益比”，表示利润相对于安全阈值的比例。

  这个和考虑了验证者 $v$ 在所有参与服务中的总影响力，加权于攻击每个服务的潜在利润。

• 右侧：$\sigma_v$

  • 这是验证者 $v$ 的总质押。

不等式表明，为了网络安全，潜在攻击利润的加权和（根据验证者在每个服务中的质押调整）不应超过验证者的总质押。

级联攻击的参考深度：兔子洞有多深？

• 参考深度：在级联攻击序列中，参考深度衡量每次攻击受到早期攻击中被罚没的验证者的影响有多深。这是一种理解网络中涟漪效应并衡量这些故障之间相互关联程度的方法。

定义：乘性松弛。
我们说重质押图 $G$ 是 $\gamma$-松弛安全的，如果对于 $G$ 上的所有攻击联盟 $(A, B)$，

$$(1 + \gamma) \cdot \pi_A \leq \sigma_B $$ 其中

破坏 $A$ 的总利润 = $\pi_A$ 且验证者 $B$ 拥有的总质押 = $\sigma_B$ (方程 11)

超额抵押提供稳健安全

引理 1

声明： 设 $G = (S, V, E, \pi, \sigma, \alpha)$ 为任意重质押图，并进一步假设 $(A, B)$ 是 $G \downarrow D$ 上的攻击联盟，其中 $D \subseteq V$。那么，$(A, B \cup D)$ 是 $G$ 上的攻击联盟。

解释：我们想证明，如果一组验证者 $B$ 可以在移除一些验证者 $D$ 的子图中攻击一组服务 $A$，那么组合集 $B \cup D$ 也可以在原始图 $G$ 中攻击 $A$。

理解组件

我们有一个重质押图 $G$，表示验证者与服务之间的交互。

子图 $G \downarrow D$：这是图 $G$，但移除了 $D \subseteq V$ 中的验证者或被罚没的验证者。攻击条件在这个缩减的图中检查。

攻击条件

对于 $(A, B)$ 成为子图 $G \downarrow D$ 上的攻击联盟，验证者 $B$ 必须控制足够的质押以满足每个服务 $A$ 的攻击阈值。数学上，这意味着：

$\sigma_{B \cap N_G(s)} \geq \alphas \cdot \sigma{N_G(s) \setminus D} \quad \forall s \in A$

这里：

• $\sigma_{B \cap N_G(s)}$ 是验证者 $B$ 中连接到服务 $s$ 的总质押。
• $\sigma_{N_G(s) \setminus D}$ 是连接到 $s$ 的验证者的总质押，不包括 $D$ 中的验证者。

证明

已知信息：

我们知道 $(A, B)$ 是子图 $G \downarrow D$ 上的攻击联盟。这意味着对于每个服务 $s \in A$：

$\sigma_{B \cap N_G(s)} \geq \alphas \cdot \sigma{N_G(s) \setminus D}$

这是起始假设。

目标：

我们需要证明联盟 $(A, B \cup D)$ 也是原始图 $G$ 上的攻击联盟。具体来说，我们想证明：

$\sigma_{(B \cup D) \cap N_G(s)} \geq \alphas \cdot \sigma{N_G(s)} \quad \forall s \in A$

这意味着当我们包括 $D$ 中的验证者时，$B \cup D$ 的总质押仍然满足每个服务 $s \in A$ 的攻击阈值。

质押计算：

对于每个服务 $s \in A$，$B \cup D$ 中连接到 $s$ 的验证者的总质押为：

$\sigma_{(B \cup D) \cap NG(s)} = \sigma{B \cap NG(s)} + \sigma{D \cap N_G(s)}$

• $\sigma_{B \cap N_G(s)}$：$B$ 中连接到 $s$ 的验证者的质押。
• $\sigma_{D \cap N_G(s)}$：$D$ 中连接到 $s$ 的验证者的质押。

结合攻击条件：

由于 $\sigma_{B \cap N_G(s)} \geq \alphas \cdot \sigma{N_G(s) \setminus D}$（来自假设），我们可以将其代入方程：

$\sigma_{(B \cup D) \cap NG(s)} = \sigma{B \cap NG(s)} + \sigma{D \cap N_G(s)} \geq \alphas \cdot \sigma{NG(s) \setminus D} + \sigma{D \cap N_G(s)}$

注意 $\sigma_{NG(s)} = \sigma{NG(s) \setminus D} + \sigma{D \cap N_G(s)}$。

简化表达式：

上述不等式可以重写为：

$\sigma_{(B \cup D) \cap N_G(s)} \geq \alphas \cdot (\sigma{NG(s)} - \sigma{D \cap NG(s)}) + \sigma{D \cap N_G(s)}$

由于 $\alphas \cdot \sigma{N_G(s)} \geq \alphas \cdot \sigma{D \cap NG(s)}$，在两边加上 $\sigma{D \cap N_G(s)}$ 确保：

$\sigma_{(B \cup D) \cap N_G(s)} \geq \alphas \cdot \sigma{N_G(s)}$

这证实了 $B \cup D$ 的总质押满足攻击 $s$ 所需的阈值。

结论：

因此，集合 $B \cup D$ 可以在原始图 $G$ 中成功攻击 $A$。

引理因此得证，因为 $(A, B \cup D)$ 确实是 $G$ 上的攻击联盟。

推论 1

声明： 设 $G = (S, V, E, \pi, \sigma, \alpha)$ 为任意重质押图，并进一步假设 $(A_1, B_1), \dots, (A_T, BT) \in \mathcal{C}(G)$ 是 $G$ 上的有效级联攻击序列。那么， $$\left( \bigcup{t=1}^{T} At, \bigcup{t=1}^{T} B_t \right)$$ 也是 $G$ 上的有效攻击。

解释： 这个推论试图证明，如果我们在网络上有一系列成功的攻击，那么我们可以将这些攻击组合成一个更大的攻击，并且它仍然会成功。本质上，它表明一系列较小的攻击可以组合成一个大的攻击，而不会失去攻击条件的有效性。

理解组件

• 重质押图 $G = (S, V, E, \pi, \sigma, \alpha)$。

• 级联攻击：

  • 级联攻击序列 $(A_1, B_1), \dots, (A_T, B_T)$ 指的是一个序列，其中每个 $(A_t, B_t)$ 是第 $t$ 步的攻击，可能由前面的攻击启用。

• 集合的并集：

  • $\bigcup_{t=1}^T A_t$ 表示序列中所有被攻击的服务的并集。
  • $\bigcup_{t=1}^T B_t$ 表示这些攻击中涉及的所有验证者的并集。

需要证明什么？

目标是证明在级联攻击中涉及的所有服务和所有验证者的组合集也形成了对原始图 $G$ 的有效攻击。具体来说，这意味着：

• 质押条件：验证者 $\bigcup_{t=1}^T Bt$ 的组合质押必须足以攻击服务 $\bigcup{t=1}^T A_t$。
• 利润条件：攻击 $\bigcup_{t=1}^T At$ 的总利润必须超过验证者 $\bigcup{t=1}^T B_t$ 的总质押。

证明分解

• 应用引理 1：

  • 通过反复应用引理 1，证明显示序列中的每一步 $(At, \bigcup{i=1}^t Bi)$ 都是 $G$ 上的攻击联盟。这是因为随着我们逐步通过每次攻击 $t$，验证者 $\bigcup{i=1}^t B_i$（那些在包括第 $t$ 步在内的攻击中涉及的验证者）足以攻击服务 $A_t$。

• 检查攻击条件（方程 1）：

  • 由于每个 $(At, \bigcup{i=1}^t B_i)$ 都是攻击联盟，根据方程 1 中的攻击条件，我们可以说这些步骤中验证者的组合质押足以攻击他们各自的服务。

• 集合的不相交性：

  • 服务 $A_t$ 和验证者 $B_t$ 在不同的 $t$ 中被认为是不相交的。这种不相交性是组合攻击集而不重叠的关键。
  • 具体来说，不相交性确保在考虑整个序列时，所有步骤的组合攻击满足有效攻击的必要条件。

• 利润与质押（方程 2）：

  • 对于组合集成为有效攻击，必须满足：

    $$\sum{t=1}^T \pi{At} > \sum{t=1}^T \sigma_{B_t}$$

  • 这意味着攻击序列中所有服务的总利润必须超过涉及攻击的验证者的总质押。

  • 由于每个单独的步骤 $(A_t, B_t)$ 满足这个条件（假设这些是有效攻击），利润的总和必然超过所有步骤的质押总和。

  • 因此，组合攻击 $\left( \bigcup_{t=1}^T At, \bigcup{t=1}^T B_t \right)$ 是原始图 $G$ 上的有效攻击，满足质押和利润条件。这完成了证明。

定理 1

声明：
假设重质押图 $G = (S, V, E, \pi, \sigma, \alpha)$ 对于某个 $\gamma > 0$ 是 $\gamma$-松弛安全的。那么，对于任何 $\psi > 0$，

$$R_\psi(G) < \left(1 + \frac{1}{\gamma}\right) \psi.$$

解释：
该定理旨在证明，如果重质押网络在乘性松弛下是安全的，那么由于初始冲击 $\psi$ 导致的质押最大损失，包括任何级联效应，都受到严格控制。具体来说，最坏情况下的损失 $R_\psi(G)$ 将最多为 $\left(1 + \frac{1}{\gamma}\right)\psi$。这意味着网络的安全性确保即使最初损失了一小部分质押，总损失也不会失控地增长。

理解组件

• 重质押图 $G = (S, V, E, \pi, \sigma, \alpha)$。

需要证明什么？

• 乘性松弛 $\gamma$：如果对于任何潜在攻击联盟 $(A, B)$（其中 $A$ 是目标服务集，$B$ 是试图攻击的验证者集），以下条件成立，则认为图是 $\gamma$-松弛安全的：

  $$(1 + \gamma) \cdot \pi_A \leq \sigma_B$$

  这意味着验证者 $B$ 控制的总质押必须大于攻击服务 $A$ 的利润 $\pi_A$，按因子 $1 + \gamma$ 缩放。$\gamma$ 项充当安全边际，确保验证者的质押显著大于攻击的潜在利润。

证明分解

初始冲击 $\psi$：

• 初始冲击 $\psi$：假设发生了一个事件，导致总质押 $\sigma_V$ 的一小部分 $\psi$ 突然损失。这种冲击可能代表任何情况，从验证者故障到外部攻击。
• 挑战在于评估这种初始损失如何通过网络传播，可能导致进一步的损失——这一过程称为级联故障。

定义子图和级联攻击：

• 为了分析初始冲击的影响，考虑子图 $G \downarrow D$，其中 $D$ 是由于初始冲击而失去质押的验证者集。因此，$G \downarrow D$ 是移除这些验证者后的图。
• 级联攻击：在这个子图中可能发生一系列攻击 $(A_1, B_1), \dots, (A_T, B_T)$。这些攻击代表初始冲击后可能发生的连续故障或攻击。

使用推论 1 聚合攻击：

• 根据推论 1，我们可以将所有级联攻击组合成原始图 $G$ 上的一个更大的攻击。定义：

  $$A := \bigcup_{t=1}^T At \quad \text{和} \quad B := \bigcup{t=1}^T B_t$$

  这个聚合集 $(A, B)$ 表示在考虑所有级联效应后对图的整体攻击。

理解攻击条件：

• 对于 $(A, B)$ 成为子图 $G \downarrow D$ 上的有效攻击，攻击服务 $A$ 的利润必须超过验证者 $B$ 持有的总质押：

  $$\pi_A > \sigma_B$$

  这个不等式表明，$B$ 单独无法覆盖攻击 $A$ 的潜在利润。

应用 $\gamma$-松弛条件：

• 由于原始图 $G$ 是 $\gamma$-松弛安全的，当我们将初始冲击 $D$ 中的验证者重新纳入方程时，松弛条件仍然成立：

  $$(1 + \gamma) \cdot \piA \leq \sigma{B \cup D}$$

  其中 $\sigma_{B \cup D} = \sigma_B + \sigma_D$ 表示攻击验证者和遭受初始冲击的验证者的组合质押。

简化和分析不等式：

• 将已知不等式 $\pi_A > \sigma_B$ 代入松弛条件：

  $$(1 + \gamma) \cdot \sigma_B < (1 + \gamma) \cdot \pi_A \leq \sigma_B + \sigma_D$$

  这告诉我们，参与级联故障的验证者的总质押不足以在考虑初始冲击后满足所需的质押阈值。

推导最坏情况损失的界限：

• 重新排列不等式：

  $$\gamma \cdot \sigma_B \leq \sigma_D$$

  由于 $\sigma_D$ 表示由于初始冲击 $\psi$ 导致的质押损失，将其表示为：

  $$\sigma_D = \psi \cdot \sigma_V \quad \Rightarrow \quad \gamma \cdot \sigma_B \leq \psi \cdot \sigma_V$$

• 通过除以 $\sigma_V$（网络中的总质押）进行归一化：

  $$\frac{\sigma_B}{\sigma_V} \leq \frac{\psi}{\gamma}$$

  这个不等式表明，由于级联故障导致的质押损失比例受初始冲击按 $\frac{1}{\gamma}$ 缩放的限制。

总结损失：

• 最后，将初始冲击 $\psi$ 和级联损失 $\frac{\sigma_B}{\sigma_V}$ 相加：

  $$\psi + \frac{\sigma_B}{\sigma_V} \leq \psi + \frac{\psi}{\gamma} = \left(1 + \frac{1}{\gamma}\right)\psi$$

  这个对总损失 $R_\psi(G)$ 的界限确保无论初始冲击和后续级联有多严重，总损失都保持在这个可预测的范围内。

定理 1 的关键见解

• 乘性松弛 $\gamma$ 提供了一个重要的安全缓冲，限制了级联故障的影响。通过要求验证者持有的质押大于攻击的潜在利润（按 $1 + \gamma$ 缩放），网络可以吸收冲击而不会引发不可控的损失。
• 受控级联：证明表明，即使在最坏的情况下，损失通过网络级联，总损失也是有界且可预测的。这个界限对于网络设计者确保区块链系统的弹性和稳定性非常重要。

推论 2

声明：
设 $G$ 为重质押图，使得对于所有验证者 $v \in V$，

$$\sum_{s \in N_G({v})} \frac{\sigmav}{\sigma{N_G({s})}} \cdot \frac{(1 + \gamma)\pi_s}{\alpha_s} \leq \sigma_v$$

那么，最坏情况下的质押损失 $R_\psi(G)$ 小于 $\left(1 + \frac{1}{\gamma}\right)\psi$。

解释：
这个推论旨在证明，如果网络中的每个验证者都满足特定的风险条件，那么整个网络是安全的。具体来说，这个条件确保即使攻击的潜在损失被松弛因子 $\gamma$ 放大，验证者的质押也始终能够覆盖这些损失。因此，网络中的最坏情况下的质押损失仍然是有界的。

理解组件

解释条件（方程 17）：

• 验证者的质押 $\sigma_v$：这是验证者 $v$ 控制的总质押。
• 服务 $s$：$N_G({v})$ 中的每个服务 $s$ 由验证者 $v$ 直接支持。
• 支持服务 $s$ 的质押比例：项 $\frac{\sigmav}{\sigma{N_G({s})}}$ 表示验证者 $v$ 对服务 $s$ 的总质押的贡献比例。这很重要，因为它根据验证者对服务安全的贡献比例来缩放每个验证者面临的风险。
• 修改后的利润项 $(1 + \gamma)\pi_s$：这个项反映了破坏服务 $s$ 的潜在利润，按乘性松弛 $\gamma$ 放大。按 $1 + \gamma$ 放大意味着即使攻击更有利可图（由于松弛），验证者仍然必须有足够的质押来覆盖这种增加的风险。

需要证明什么？

• 不等式表明，验证者 $v$ 在所有支持服务中的潜在损失总和（按松弛调整的利润项计算）不应超过验证者自己的质押。如果这对每个验证者都成立，那么网络是安全的。

这个条件如何确保安全？

• 每个验证者的风险控制：如果每个验证者的总质押能够覆盖支持所有连接服务的最坏情况（考虑松弛），那么没有单个验证者会过度暴露于风险。这种在验证者层面的控制直接支持了网络的全局安全。
• 防止级联：通过确保没有验证者相对于他们支持的服务过度杠杆化，这个条件有助于防止一个验证者的失败可能引发进一步损失的连锁反应。

证明分解

连接到定理 1 和 Claim 1：

• 定理 1 回顾：定理 1 指出，如果整个网络是 $\gamma$-松弛安全的，那么最坏情况下的损失 $R_\psi(G)$ 以 $\left(1 + \frac{1}{\gamma}\right)\psi$ 为界。
• Claim 1：这个声明（此处未完全详细说明，但在证明中引用）可能提供了一个充分条件，确保在利润按 $1 + \gamma$ 缩放时不存在有效攻击。
• 应用到推论 2：证明显示，如果每个验证者满足方程 17 中的条件，这意味着整个网络在松弛调整条件下是安全的。本质上，方程 17 是定理 1 中全局安全条件的局部版本。通过应用 Claim 1 中的条件，确保在调整利润下没有有效攻击，推论得出结论，网络的最坏情况损失如定理 1 所述保持有界。

推论 2 的关键见解

• 如果每个验证者都满足方程 17 中的局部风险条件，整个网络保证能够抵抗大规模的级联损失。按松弛调整的攻击潜在利润永远无法压倒验证者的质押，从而确保网络保持稳健。
• 在实践中，这意味着网络设计者可以通过验证所有验证者是否满足这个条件来确保安全性，这比直接检查整个网络的安全性要容易得多。

全局安全的下界

定理 2

声明：
对于任何 $0 < \epsilon < 1$，存在一个重质押图 $G$，它是安全的并满足 EigenLayer 条件（如方程 3 中所述），但对于所有 $\psi \geq \epsilon$，$R_\psi(G) = 1$。

解释： 这个定理断言，即使重质押图 $G$ 满足 EigenLayer 提出的安全条件（如方程 3 中定义），网络仍然可能经历灾难性损失，其中最坏情况下的质押损失 $R_\psi(G)$ 等于 $1$，意味着整个质押可能丢失，如果初始冲击 $\psi$ 超过某个阈值 $\epsilon$。简而言之，这个定理突出了一个场景，即满足安全条件不足以在某些情况下防止网络完全失败。

理解组件

• 考虑重质押图 $G = (S, V, E, \pi, \sigma, \alpha)$。

• 服务： $S$ = { $x$ }，只有一个服务 $x$。

• 验证者： $V$ = { $a, b$ }，有两个验证者，$a$ 和 $b$。

• 边： 每个验证者通过边连接到服务 $x$，所以 $E$ = { $(x, a), (x, b)$ }。

• 定义质押和参数：

• $\sigma_a = \epsilon$（验证者 $a$ 的质押）。

• $\sigma_b = 1 - \epsilon$（验证者 $b$ 的质押）。

• $\pi_x = 1$（攻击服务 $x$ 的利润）。

• $\alpha_x = 1$（攻击服务 $x$ 所需的总质押比例）。

• 我们假设 $\psi < 1$，因为对于任何重质押图 $G$，$R_1(G) = 1$。这个假设简化了分析，并专注于小于总质押的冲击。

证明分解

• 将 EigenLayer 条件（Claim 1）应用于验证者 $a$ 和 $b$：

  • EigenLayer 条件指出，如果对于每个验证者 $v \in V$，

  $$\sum_{s \in N_G({v})} \frac{\sigmav}{\sigma{N_G({s})}} \cdot \frac{\pi_s}{\alpha_s} \leq \sigma_v$$

  • 对于验证者 $a$：

  $$\frac{\sigma_a}{\sigma_a + \sigma_b} \cdot \frac{\pi_x}{\alpha_x} = \frac{\epsilon}{\epsilon + (1 - \epsilon)} \cdot 1 = \epsilon$$

  这等于 $\sigma_a$，满足条件。

  • 对于验证者 $b$：

  $$\frac{\sigma_b}{\sigma_a + \sigma_b} \cdot \frac{\pi_x}{\alpha_x} = \frac{1 - \epsilon}{\epsilon + (1 - \epsilon)} \cdot 1 = 1 - \epsilon$$

  这等于 $\sigma_b$，也满足条件。

• 由于两个验证者都满足条件，重质押图 $G$ 根据 Claim 1 是安全的。

• 引入初始冲击 $D = {a}$：

  • 考虑初始冲击 $D = {a}$，意味着验证者 $a$ 失去了其全部质押 $\sigma_a = \epsilon$。
  • 由于 $\sigma_a / \sigma_V = \epsilon / (\epsilon + (1 - \epsilon)) = \epsilon \leq \psi$，这个冲击符合冲击 $\psi$。

• 冲击后的结果图：

  • 移除 $a$ 后，剩余图 $G \downarrow D$ 由服务 $x$ 和仅由验证者 $b$ 支持。

• 确定攻击条件：

  • 对 $({x}, {b})$ 表示 $G \downarrow D$ 上的攻击联盟。
  • 由于 $b$ 是唯一支持 $x$ 的剩余验证者，如果 $\sigma_b < \pi_x$，攻击可以成功。由于 $\sigma_b = 1 - \epsilon$ 且 $\pi_x = 1$，这个条件成立。- 计算最坏情况下的质押损失：
  • 冲击 $D = {a}$ 后的总质押为 $\sigma_b = 1 - \epsilon$。
  • 由于 $b$ 不足以完全保护 $x$，攻击成功，导致总质押损失为 $R_\psi(G) \geq \frac{\sigma_a + \sigma_b}{\sigma_V} = \frac{1}{1} = 1$。

定理 2 的关键见解

• 因此，证明表明，即使图 $G$ 满足 EigenLayer 条件，当初始冲击 $\psi$ 足够大时，它仍然容易遭受总损失。
• 具体来说，对于任何 $\psi \geq \epsilon$，整个网络的质押可能会被完全抹去，验证了定理的陈述，即对于 $\psi \geq \epsilon$，$R_\psi(G) = 1$。

定理 3

陈述：
对于任何 $\psi$，$\gamma$，$\epsilon > 0$，使得

$$0 \leq \left( 1 + \frac{1}{\gamma} \right) \psi - \epsilon \leq 1 $$

存在一个重新质押图 $G$，满足推论 2 中的条件 $(17)$，但 $R_{\psi}(G) \geq \left( 1 + \frac{1}{\gamma} \right) \psi - \epsilon$。

解释：

定理 3 表明，即使重新质押图 $G$ 满足推论 2中的安全条件，它仍然可能遭受重大损失。具体来说，该定理断言，可能存在一个图，其中最坏情况下的损失 $R_\psi(G)$ 至少为 $\left(1 + \frac{1}{\gamma}\right)\psi - \epsilon$，这表明推论 2中的安全条件不足以在存在冲击 $\psi$ 时完全防止重大损失。

理解组件

• 图组件：

  • 图 $G = (S, V, E, \pi, \sigma, \alpha)$ 的构造如下：
  • 服务： $S$ = { $x$ }（一个服务 $x$）。
  • 验证者： $V$ = { $a, b, c$ }（三个验证者：$a$、$b$ 和 $c$）。
  • 边： 每个验证者通过边 $E$ = { $(x, a), (x, b), (x, c)$ } 连接到单一服务 $x$。

• 质押和参数：

  • 质押：
  • $\sigma_a > 0$：假设 $\sigma_a$ 是任意正常数。
  • $\sigma_b = \sigma_a \left( \frac{1}{\gamma} - \frac{\epsilon}{\psi} \right)$：验证者 $b$ 的质押。
  • $\sigma_c = \sigma_a \left( \frac{1 - \psi + \epsilon}{\psi} - \frac{1}{\gamma} \right)$：验证者 $c$ 的质押。
  • 服务利润： $\pi_x = \left(1 + \frac{1}{\gamma}\right)\psi - \epsilon$（攻击服务 $x$ 的利润）。
  • 安全要求： $\alpha_x = 1$（破坏服务 $x$ 所需的总质押比例）。

证明分解

• 验证者 $b$：

  • 通过条件 $\epsilon \leq \frac{\psi}{\gamma}$ 确保质押 $\sigma_b \geq 0$，保证 $b$ 具有非负质押。

• 验证者 $c$：

  • 类似地，通过不等式 $1 \geq \left(1 + \frac{1}{\gamma}\right)\psi - \epsilon$ 确保 $\sigma_c \geq 0$，确认 $c$ 具有非负质押。

• 总质押：

  • 冲击前的网络总质押为 $\sigma_V = \sigma_a + \sigma_b + \sigma_c$。

  $$\sigma_V = \sigma_a + \sigma_b + \sigma_c = \sigma_a \left( \left(1 + \frac{1}{\gamma}\right) - \frac{\epsilon}{\psi} + \frac{1 - \psi + \epsilon}{\psi} - \frac{1}{\gamma} \right) = \frac{\sigma_a}{\psi}$$

• 验证者 $a$：

  • 推论 2 中的条件要求每个验证者 $v$ 满足：

  $$\sum_{s \in N_G({v})} \frac{\sigmav}{\sigma{N_G({s})}} \cdot (1 + \gamma)\pi_s \leq \sigma_v$$

  • 对于验证者 $a$，代入值确认：

  $$\sigma_a = \sigma_a$$

  因此，条件得到满足。

• 验证者 $b$：

  • 对验证者 $b$ 的类似计算表明，推论 2 中的条件也得到满足。

• 初始冲击 $D$ = { $a$ }：

  • 冲击 $D$ = { $a$ } 从网络中移除验证者 $a$ 及其质押 $\sigma_a$。剩余的验证者 $b$ 和 $c$ 现在支持服务 $x$。

• 验证者 $b$ 的攻击激励：

  • 冲击后，我们需要确定验证者 $b$ 是否有动力攻击服务 $x$。如果攻击 $x$ 的预期利润超过其剩余质押，验证者 $b$ 将发起攻击：

  $$\pi_x - \sigma_b > 0$$

  • 代入值后，表达式变为：

  $$\pi_x - \sigma_b = \left[\left(1 + \frac{1}{\gamma}\right)\psi - \epsilon\right] - \left[\frac{\sigma_a}{\gamma} - \frac{\sigma_a \epsilon}{\psi}\right]$$

  进一步简化：

  $$\pi_x - \sigma_b = \gamma \epsilon \cdot \frac{\sigma_a}{(1 + \gamma)\psi} > 0$$

  • 由于表达式为正，验证者 $b$ 确实有动力攻击服务 $x$。

• 计算损失 $R_\psi(G)$：

  • $b$ 攻击后，总损失为：

  $$R_\psi(G) \geq \frac{\sigma_a + \sigma_b}{\sigma_V} = \left(1 + \frac{1}{\gamma}\right)\psi - \epsilon$$

  • 这证明了网络遭受了重大损失，正如定理所述。

定理 3 的关键见解

• 定理 3 表明，可以构造一个满足推论 2中安全条件的重新质押图 $G$，但在受到重大冲击 $\psi$ 时仍然会遭受重大损失。这揭示了该条件的一个关键漏洞，表明在某些情况下，它不足以防止大规模故障。证明强调了开发更强大的安全措施的重要性，这些措施应超越推论 2提供的条件，确保去中心化网络在灾难性事件中的弹性。

本地安全

定理 4

陈述： 对于任何本地安全条件 $f$，任何安全的重新质押图 $G$，以及服务联盟 $C \subseteq S$ 使得 $f(C, G) = 1$，存在一个安全的 $C$-本地变体 $G'$，使得 $R_0(C, G') = 1$。

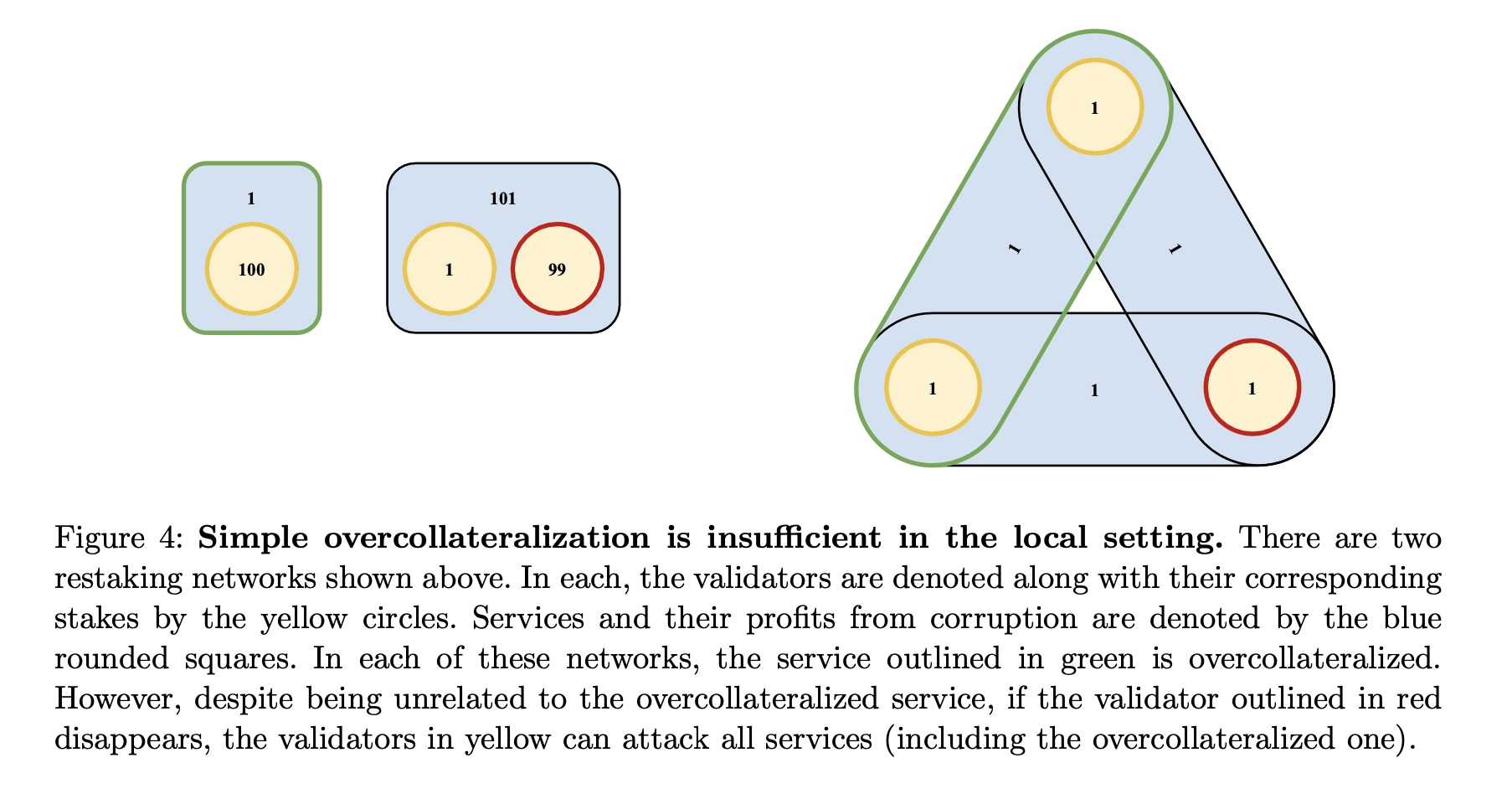
解释： 定理 4 证明，对于任何安全的重新质押网络配置，我们总是可以构造一个网络变体，其中服务联盟 $C$ 可以经历最坏情况下的质押损失场景。这是通过操纵超额质押并引入新的服务和验证者来实现的，以在增强图 $G'$ 上设计有效的攻击。

证明分解

定义总超额质押 $\Delta$：

• $\Delta = \sigma_{N_G C} - \pi_C$：

  • $\sigma_{N_G C}$：来自联盟 $C$ 邻域中验证者的总质押，即直接保护 $C$ 中服务的验证者。
  • $\pi_C$：通过破坏联盟 $C$ 可以获得的利润，本质上是攻击者可以获得的收益。

• $\Delta$ 表示保护联盟 $C$ 的额外质押，这对于理解 $C$ 中的服务是否超额质押（安全）非常重要。

增强图 $G$ 以创建 $G'$：

• 证明通过添加一个新服务 $s^*$ 和两个验证者 $a$ 和 $b$ 来创建一个增强图 $G'$，这两个验证者仅与新服务 $s^*$ 相邻。

• 新验证者质押：

  • $\sigma_a = \Delta + \epsilon$：验证者 $a$ 的质押是 $C$ 的超额质押加上一个小量 $\epsilon$，确保 $a$ 的质押足够大。
  • $\sigma_b = \epsilon$：验证者 $b$ 有一个小质押 $\epsilon$，用于控制新攻击结构的一部分。

• 新服务 $s^*$ 的利润：
  新服务 $s^*$ 的破坏利润为 $\pi_{s^*} = \Delta + 2\epsilon$，确保其利润潜力与 $C$ 的超额质押直接相关。

攻击的有效性：

• 验证者 $a$ 不与联盟 $C$ 路径连接，这意味着没有其他验证者依赖 $a$ 来保护 $C$ 中的服务。

• 这很重要，因为它保证了修改 $a$ 的质押或安全设置不会影响图 $G$ 中 $C$ 的原始安全结构。

• 通过构造，攻击 $(C \cup {s^*}, N_G C \cup {b})$ 在新图 $G'$ 上是有效的，这意味着攻击可能导致最坏情况下的最大损失 $R_0(C, G') = 1$。

• 这证明，对于任何本地安全条件 $f$，总是存在一个修改后的图 $G'$，其中联盟 $C$ 的最坏情况会导致最大质押损失。

定理 4 的关键见解

• 即使服务联盟 $C$ 是安全的，定理 4 表明，总是可以通过稍微修改网络——通过添加一个新服务和一些验证者——使得 $C$ 的最坏可能损失变得尽可能大。在这个修改后的网络中，安全性变得本地化于 $C$，并且联盟 $C$ 可能会遭受最大损失。

稳定攻击的本地安全条件

定理 5

陈述：在重新质押图 $G$ 中，设 $C \subseteq S$ 为服务联盟。如果对于所有攻击头 $(X, Y)$，其中 $X \subseteq C$，不等式 $(1 + \gamma) \pi_X \leq \sigmaY$ 成立，那么联盟 $C$ 的最坏情况损失 $R\psi(C, G)$ 严格小于 $\left(1 + \frac{1}{\gamma} \right)\psi$。此外，检查此不等式是否对所有攻击头成立的函数是一个本地安全条件。

解释：定理 5 保证了一个充分质押的网络可以限制任何攻击的潜在损失，并提供了检查此条件的本地方法，使其在保护区块链网络的实际应用中更加实用。

证明分解

限制最坏情况损失的条件：

• 需要满足的条件是：

  $$(1 + \gamma)\pi_X \leq \sigma_Y$$

  这个不等式表明，保护 $X$ 中服务的验证者的质押必须足够大，以覆盖破坏这些服务的潜在利润，并按安全边际 $\gamma$ 进行缩放。这确保了攻击者无法轻易利用服务联盟 $C$，因为验证者有足够的质押来抵御攻击。

攻击序列和验证者损失：

• 证明考虑了联盟 $C$ 上任意级联攻击序列，表示为 $(A_1, B_1), \dots, (A_T, B_T)$，其中每次攻击都涉及服务子集 $A_t$ 被攻击，验证者 $B_t$ 可能失去其质押。

• 对于每个攻击步骤 $t$，定义集合 $L_t$，表示在该特定攻击中丢失的验证者。这些是专门保护 $C$ 中服务并在攻击中被破坏的验证者。

服务 $A_t'$ 的最大集合：

• 证明引入了集合 $A_t'$，定义为在每个步骤中仍可被视为攻击联盟的服务子集。这些服务由 $B_t$ 和其他剩余验证者的组合保护。

• $A_t'$ 中的服务满足条件：

  $$\sigma_{B_t \setminus L_t} \geq \alphas \cdot \sigma{NG{s} \setminus \left( \bigcup{i=1}^{t-1} B_i \cup D \right)}$$

  这意味着剩余的验证者 $B_t \setminus L_t$ 提供了足够的质押，以满足 $A_t'$ 中服务的攻击抵抗要求。

• 证明通过展示在条件 $(1 + \gamma) \pi_X \leq \sigmaY$ 下，最坏情况损失 $R\psi(C, G)$ 严格小于 $\left( 1 + \frac{1}{\gamma} \right)\psi$ 来得出结论。换句话说，联盟 $C$ 的最大可能质押损失得到了有效控制和限制。

• 此外，检查此条件是否对所有攻击头成立的函数是一个本地安全条件。这意味着它可以通过仅检查 $C$ 的邻域中的服务和验证者来验证，而无需考虑整个网络。

定理 5 的关键见解

定理 5 提供了一个框架，通过确保验证者有足够的质押来覆盖对服务联盟的任何潜在攻击，从而限制重新质押网络中的最坏情况损失。具体来说，它表明：

• 如果验证者的质押大于所有可能攻击场景的攻击利润，联盟的最坏情况损失将不会超过特定的上限。这确保了网络在面对攻击时保持弹性。

• 检查此条件是否成立的过程是本地化的，这意味着它可以通过仅关注相关服务和验证者子集来高效完成，而无需分析整个网络。

本地安全的下界

定理 6

陈述：
对于任何 $\gamma > 0$，存在一个重新质押图 $G = (S, V, E, \pi, \sigma, \alpha)$，满足推论 2 中的条件 (17)，但也存在一个联盟 $C \subseteq S$，使得最坏情况损失 $R_0(C, G) = 1$。

解释：
这意味着，即使图满足某些服务的安全条件，仍然可能存在一个服务子集在最坏情况下的攻击场景中经历最大可能的损失。

证明分解

定义重新质押图：

• 服务和验证者：
  设服务为 $S = {x, y, z}$，验证者为 $V = {a, b, c}$。边 $E$ 定义了哪些验证者保护哪些服务，它们由以下给出：

  $$E = {(x, a), (x, b), (y, b), (y, c), (z, c), (z, a)}$$

  这创建了一个循环模式，其中每个验证者负责保护两个服务。

• 设置质押和利润参数：

  • 将每个服务的利润设置为 $\pi_x = \pi_y = \pi_z = \pi$，其中 $\pi > 0$ 是任意正常数。
  • 将验证者 $a$ 的质押设置为 $\sigma_a$，并选择 $\sigma_a$ 使得：

  $$\sigma_a < 2\pi$$

  • 将验证者 $b$ 和 $c$ 的质押设置为：

  $$\sigma_b = 2(1 + \gamma)\pi, \quad \sigma_c = 2(1 + \gamma)\pi$$

检查推论 2 中的安全条件 (17)：

• 必须满足推论 2 中的安全条件 (17)，以确保验证者的质押足以保护服务。我们需要验证给定质押值是否满足此条件。

• 对于验证者 $a$：

  $$\frac{\sigma_a}{\sigma_a + \sigma_b} \cdot (1 + \gamma)\pi + \frac{\sigma_a}{\sigma_a + \sigma_c} \cdot (1 + \gamma)\pi < (1 + \gamma)\pi$$

  简化此表达式确保验证者 $a$ 的质押满足安全条件。

• 对于验证者 $b$ 和 $c$，检查类似的不等式：

  $$\frac{\sigma_b}{\sigma_a + \sigma_b} \cdot (1 + \gamma)\pi + \frac{\sigma_b}{\sigma_b + \sigma_c} \cdot (1 + \gamma)\pi < \sigma_b$$

  $$\frac{\sigma_c}{\sigma_a + \sigma_c} \cdot (1 + \gamma)\pi + \frac{\sigma_c}{\sigma_b + \sigma_c} \cdot (1 + \gamma)\pi < \sigma_c$$

  这些不等式确认图满足条件 (17)，意味着在正常情况下，验证者的质押足以保护服务。

定义联盟 $C$：

• 设 $C = {x, z}$ 为在潜在攻击中将被针对的服务联盟。

• 考虑冲击 $D = {b, c}$，其中验证者 $b$ 和 $c$ 经历故障或攻击。由于它们的质押较大，它们的故障可能导致级联损失。

建立最大损失：

• 由于 $\sigma_a < 2\pi$ 且 $\pi_x + \pi_z = 2\pi$，验证者 $a$ 的质押不足以覆盖破坏服务 $x$ 和 $z$ 的总利润。

• 因此，集合 ${x, z}$ 和验证者 ${a}$ 形成一个稳定的攻击联盟，导致服务联盟 $C = {x, z}$ 的最大损失。

• 冲击 $D = {b, c}$ 移除验证者 $b$ 和 $c$，仅留下 $a$ 来保护 $C$。由于 $a$ 的质押不足，$C$ 中的服务被破坏，$R_0(C, G) = 1$。

定理 6 的关键见解

定理 6 表明，即使重新质押图满足推论 2 中的安全条件，仍然可能存在一个服务联盟在特定攻击场景中经历最坏情况下的损失。具体来说，这表明：

• 安全条件可以在全局上得到满足，但仍然可能存在局部漏洞，使得服务子集 $C$ 容易遭受灾难性损失。

• 通过仔细构造质押分布和服务-验证者连接，可以创建特定服务子集 $C$ 容易受到攻击的场景，尽管整个网络看起来是安全的。

长级联

定理 7

陈述：假设重新质押图 $G = (S, V, E, \pi, \sigma, \alpha)$ 对于某个 $\gamma > 0$ 是安全的，具有 $\gamma$-松弛。设 $\sigma_V$ 表示任何验证者持有的最小质押。对于任何 $\psi > 0$，设 $B0 \in D\psi(C, G)$ 表示初始扰动或受损验证者集合。那么对于参考深度 $k$，攻击轮数 $T$ 必须满足：

$$T < k \left( 1 + \log_{1 + \gamma} \frac{\psi \cdot \sigma_V}{\epsilon \gamma} \right)$$

其中 $\epsilon$ 表示网络中级联故障的阈值。

解释：定理 7 保证，虽然攻击可以通过重新质押网络传播，但它不能无限传播。系统设计为限制攻击可以持续的轮数，确保网络最终稳定并避免全面崩溃。

证明分解

参考深度和攻击级联：

• 该定理通过关注参考深度 $k$ 来分析攻击如何通过网络传播，参考深度 $k$ 衡量攻击可以深入系统的程度。级联影响被分解为多个阶段或攻击轮。

• 对于每个攻击序列 $(A_1, B_1), \dots, (A_T, B_T)$，攻击从初始扰动 $B_0$ 传播，并在每轮中破坏额外的验证者。

• 攻击必须满足基于验证者质押、松弛因子 $\gamma$ 和攻击可以进展的阶段的某些约束。

攻击传播和验证者损失：

• 在每个阶段 $i$，保护攻击序列 $A_i$ 中服务的验证者丢失，导致级联故障。集合 $A_i'$ 和 $B_i'$ 分别表示每轮中被破坏的最大服务和验证者集合。

• 通过应用推论 1 中的条件，我们可以验证攻击序列的每个阶段都是对重新质押图 $G$ 的有效攻击，并计算每轮中丢失的验证者数量。

• 攻击通过系统中的验证者和服务传播，但基于可用质押和安全条件，攻击可以发生的轮数存在约束。

每个阶段攻击的有效性：

• 证明通过多次应用推论 1 确保攻击序列保持有效。在每个阶段，条件必须成立，意味着被破坏验证者的质押超过未来阶段中保护剩余验证者所需的累积质押。

$$\sigma_{Bt'} > \gamma \sum{j=i+1}^{\lfloor T/k \rfloor} \sigma_{B_j'}$$

• 这确保攻击的每个阶段都有足够的影响以继续传播，但攻击轮数受松弛因子 $\gamma$ 的约束。

归纳论证和攻击轮数的上限：

• 证明通过使用归纳论证得出结论，表明攻击序列导致每个阶段被破坏验证者的质押减少。序列 $X_i$ 定义为测量每个步骤的剩余质押，从初始质押 $X_0$ 开始。

• 攻击总轮数 $T$ 受参考深度 $k$ 和对数因子的限制，对数因子涉及最小验证者质押 $\sigma_V$、扰动大小 $\psi$ 和松弛因子 $\gamma$。

攻击轮数 $T$ 的最终界限：

• 最终结果表明，攻击轮数 $T$ 必须满足不等式：

  $$T < k \left( 1 + \log_{1 + \gamma} \frac{\psi \cdot \sigma_V}{\epsilon \gamma} \right)$$

  这意味着攻击不能无限继续，轮数受网络安全条件的限制。松弛因子 $\gamma$ 和最小验证者质押 $\sigma_V$ 在限制攻击传播中都起着关键作用。

定理 7 的关键见解

定理 7 提供了重新质押网络中攻击轮数的上限。它表明：

• 攻击受验证者质押和松弛的限制

  • 攻击通过网络传播受最小验证者质押和安全缓冲 $\gamma$-松弛的限制。

• 级联故障是有界的

  • 虽然攻击可能通过网络传播，但攻击可以传播的阶段或轮数是有限的。这确保了系统可以在有限轮数后恢复，而不是经历无限制的崩溃。

• 安全条件控制攻击的深度

  • 攻击的深度（传播多远）由参考深度 $k$ 和对数因子控制，对数因子涉及验证者质押和松弛。具有较大松弛或更好质押验证者的网络可以在不经历灾难性故障的情况下抵御更深的攻击。

有界利润-质押比率下的下界

定理 8

陈述： 对于任何 $0 < \epsilon < 1$，存在一个安全的重新质押图 $G = (S, V, E, \pi, \sigma, \alpha)$，满足 EigenLayer 条件（由方程 (3) 表示），且比率 $\max_{(s, v) \in S \times V} \frac{\pi_s}{\sigma_v} = 2$。然而，存在适当的子集 $C \subset S$，使得最坏情况损失 $R0(C, G) = 1$，意味着子集 $C$ 的最大损失。此外，对于任何 $\psi \geq \epsilon$，级联损失 $R\psi(S, G) = 1$，意味着对于足够大的扰动，整个图可能会经历级联故障。

解释：定理 8 表明，虽然网络在整体上可能看起来是安全的，但仍然可能存在某些服务子集容易遭受全面故障的漏洞。此外，大的扰动可能导致这些漏洞传播，导致整个网络的广泛损失。

证明分解

设置图结构：

• 选择验证者 $V$ 和服务 $S$：
  设 $n$ 表示验证者数量，并选择 $n$ 使得 $n$ 可被 6 整除（即 $6 \mid n$）。验证者集合 $V$ 由 $n$ 个验证者组成，每个验证者的质押 $\sigma_v = 1$。

  接下来，定义服务集合 $S$ 由 $3N$ 个服务组成，其中 $N = \frac{n}{6}$。每个服务 $s \in S$ 的破坏利润 $\pi_s = 2$，参数 $\alpha_s = 1$。

划分服务：

• 将服务 $S$ 分为两个不相交的集合：
  • $S_6$ 包含 $N$ 个服务，其中 $S_6$ 中的每个服务保护 6 个验证者。
  • $S_3$ 包含剩余的 $2N$ 个服务，其中 $S_3$ 中的每个服务保护 3 个验证者。

定义图中的边：

• 边 $E$ 被定义为创建单个连通组件：

  • 对于 $S_6$ 中的服务，边的绘制使得邻域 $N_G{s}$ 将验证者集合 $V$ 划分为 6 个组。
  • 对于 $S_3$ 中的服务，边的绘制使得 $N_G{s}$ 将验证者划分为 3 个组。

• 这种配置确保每个验证者 $v \in V$ 与 $S_6$ 中的一个服务和 $S_3$ 中的一个服务相邻。

满足 EigenLayer 条件 (3)：

• 为了检查是否满足 EigenLayer 条件，我们评估任何验证者 $v \in V$ 的安全方程：

  $$\sum_{s \in N_G{v}} \frac{\sigmav}{\sigma{N_G{s}}} \cdot \frac{\pi_s}{\alpha_s} = \frac{1}{6} \cdot 2 + \frac{1}{3} \cdot 2 = \sigma_v$$

  由于每个验证者连接到 $S_6$ 中的一个服务和 $S_3$ 中的一个服务，左侧的总和等于验证者的质押 $\sigma_v = 1$。这确认了图满足 EigenLayer 条件。

展示子集 $C$ 的最大损失：

• 该定理构造了子集 $C \subset S$，其中发生最坏情况损失。具体来说，它识别了服务子集 $C$，其中整个子集被破坏，导致最大损失 $R_0(C, G) = 1$。

• 服务和验证者的配置确保，如果扰动 $\psi$ 影响正确的服务集合，它可能导致保护这些服务的验证者的全部质押损失。

$\psi \geq \epsilon$ 时的级联故障：

• 当扰动 $\psi$ 超过阈值 $\epsilon$ 时，网络会经历级联故障。对服务子集的初始攻击会触发连锁反应，导致整个图 $G$ 崩溃，导致 $R_\psi(S, G) = 1$。

• 这表明，即使图满足 EigenLayer 条件，它仍然容易受到大扰动的影响，这些扰动可能会通过网络传播。

定理 8 的关键见解

定理 8 提供了关于重新质押网络漏洞的重要见解，即使它们满足像 EigenLayer 条件这样的重要安全条件。具体来说，它表明：

• 全局安全并不能防止局部故障
  • 即使网络整体满足 EigenLayer 条件，仍然可以识别出在

• 原文链接： github.com/thogiti/thogi...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～