Solana中的擦除编码是如何工作的 - 对 Reed–Solomon 编码和数据传播的深入探讨

  • thogiti
  • 发布于 2025-02-06 18:28
  • 阅读 55

该文章深入探讨了Solana区块链的高吞吐量和即时最终性，重点介绍了冗余编码（特别是Reed-Solomon编码）在应对数据丢失和网络延迟方面的重要性。文章详细阐述了Solana的账本架构、块传播协议Turbine的工作原理，以及冗余编码的机械原理、代码实现和性能优化策略。

Solana 实现了高吞吐量和近乎即时的确认，但它也必须处理实际网络的现实：数据丢失、延迟和潜在的对抗行为。使用的一项关键策略是纠删编码——具体来说，是 Reed–Solomon 代码——这允许在一些数据包丢失的情况下恢复一个区块（或分片集）。

在这篇博客文章中，我们将探讨：

  • Solana 的高层账本架构。
  • Turbine，它的区块传播协议
  • Reed–Solomon 编码背后的机制和数学。
  • 包含图表的详细代码演练，以说明编码和解码流程。
  • Solana 如何选择不同的纠删批大小，并保持一致的恢复概率。
  • 对性能、挑战和未来方向的展望。

介绍

Solana 每秒处理数千个交易，在不到一秒的时间内完成最终确认——同时容忍数据包丢失和其他网络问题。纠删编码在这种弹性中起到核心作用。通过添加少量的奇偶校验数据，丢失的部分可以在不要求领导者重新发送整个区块的情况下被恢复。

我的上一篇文章，从基本原理理解纠删编码，深入探讨了纠删编码的数学基础。如果你对从基本原理理解纠删编码的工作原理感兴趣，这是一个很好的起点。

可扩展性三难问题与 Solana

去中心化的区块链网络通常面临可扩展性三难问题：平衡速度、安全性和去中心化。Solana 通过以下方式解决这一问题：

  • 历史证明（Proof of History, PoH）：一种轻量级、可验证的时间戳机制，通过时间对交易进行排序，而不依赖于完全的区块间隔。
  • Turbine：一种基于树的广播协议，用于高效分发网络中的数据片。
  • Gulf Stream：一种将交易直接推送给领导者的系统（绕过传统的内存池），减少确认时间。
  • Reed–Solomon 纠删编码：确保即使数据包丢失，数据也可用，这是本文的重点。

Solana 的账本架构

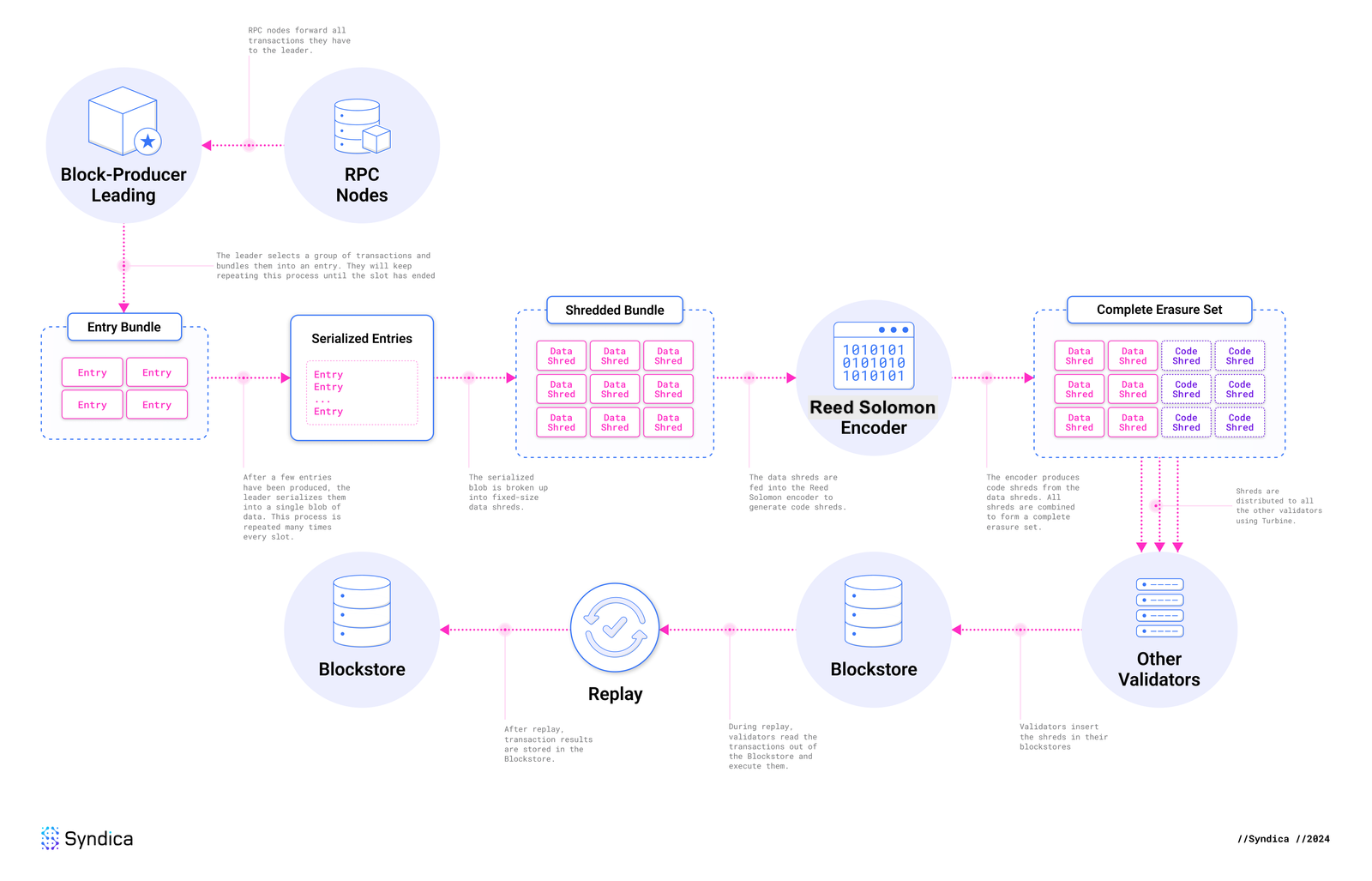Solana 的账本架构 流程 - Solana 的账本架构，来源：syndica.io

Blockstore：Solana 的去中心化数据库

首先，让我们理解 Solana 账本架构的完整流程。

每个验证者在 Solana 中运行一个 Blockstore，它管理：

  • Shreds：原子的数据显示单位（大约 1-2 KB）。
  • Entries：小批量交易。
  • Blocks：每个时隙的条目（或分片）的集合（约 ~400 ms）。
  • Metadata：包括交易状态、区块时间等。

Solana 的 Blockstore 通常使用经过优化以支持大吞吐量的键值或列式数据库实现（例如，RocksDB）。

交易和区块

  • 交易生命周期

    • 用户签署交易并提交给 RPC 节点。
    • 领导者执行交易并将其附加到区块中。
    • 其他验证者重新执行（重播）交易以确认结果，达成共识。

  • 区块创建

    • 时隙（~400 ms）：每个时隙对应于指定领导者生成的一个区块。
    • 纪元（~2 天）：包含约432,000个时隙；领导者通过基于股份加权的过程进行调度。
    • 原子区块：所有包含的交易必须有效；否则，整个区块将失效。

条目和分片

  • 条目

    • 领导者持续生成条目，每个条目包含一批交易。

  • 分片

    • 数据分片：包含大约 1228 字节的原始交易数据。
    • 编码分片：通过 Reed–Solomon 编码从数据分片计算出的奇偶校验数据（用于恢复）。

一个典型的“纠删集合”可能是 32 个数据分片 + 32 个编码分片（32:32），但 Solana 可以变更比率（参见 纠删批大小选择）。

Turbine：Solana 的区块传播协议

Turbine 是分片（数据和编码）广播给所有验证者的机制。其核心思想是将网络组织成一棵树，而不是依赖于“一个对所有”或简单的八卦机制。通过这样做，Solana 减轻了任何单一节点的带宽负担，并改善了可扩展性。

Turbine 树：根节点和层次形成

当领导者完成生成和纠删编码一个分片组后，它将这些分片通过网络数据包发送给一个特殊的根节点。该根节点负责确定哪些验证者将参与第一个数据中继层。整个过程包括：

  • 列表创建：
    根节点收集所有活动验证者的列表。然后根据股权权重对该列表进行排序，优先考虑股权较高的节点。其原则是，高股权的验证者一旦收到分片，可以快速验证并回应自己的投票，从而加快共识速度。

  • 列表洗牌：
    为了避免静态和可能被利用的树结构，排列后的列表以确定性方式洗牌。洗牌过程使用来源于 slot leader 的身份证、当前时隙编号、分片索引 和 分片类型 的因子派生的随机数种子。这样，每个分片组都有自己的 Turbine 树，同时仍足够可预测，诚实参与者可以知道他们的位置。

  • 层次形成：
    最后，根据 DATA_PLANE_FANOUT 参数将节点拆分成多层。Solana 当前的扇出值为 200 通常会导致 2 或 3 层的树：

    • 领导者 → 根节点
    • 根节点 → 第一层
    • 第一层 → （可能）第二层

    由于这一相对较大的扇出，大多数验证者与领导者之间只需两个跳（通常为 2 或 3 跳），有助于分片快速传播到整个网络。

Turbine 树使每个验证者能够准确确定下一个将转发分片的位置。这种方法在速度（高扇出）和弹性（基于股权的优先级、按分片随机化）之间取得了平衡。在实践中，这导致了低延迟的多跳传播，可以在几毫秒内饱和全球网络。

回退：八卦和修复

如果一个节点未能接收到足够的分片以重构区块（例如，网络问题或丢失率超过了 FEC 比率），它可以：

  • 直接请求领导者 retransmission，或
  • 使用确定性的 Turbine 修复：任何完全重构区块的节点都可以根据请求提供缺失的分片。这种按需“修复”过程扩展了数据在需要的 Turbine 树分支下的分布。

Turbine 中的纠删编码

让我们看看纠删编码在 Turbine 中是如何工作的。

  • 领导者将区块的条目拆分成数据分片并计算编码分片（Reed–Solomon 奇偶校验）。
  • 数据分片和编码分片同时在树中传播。即使某些分支丢失了一些数据分片，只要收到足够的奇偶校验分片，通常也能在本地恢复它们。
  • 这种方法意味着网络不需要依赖领导者重新广播缺失的数据。任何拥有足够数据和编码分片的节点都可以重建缺失的部分。

分片传播工作流程

虽然之前的两个部分描述了“为什么”和“如何”，让我们更仔细地看一下逐步流程：

  • 序列化和分片：
    领导者将区块条目拆分为数据分片（每个约 1228 字节，加上头部）。
  • 生成编码分片：
    对于每组（前向纠错集或“FEC 集”）的数据分片，应用 Reed–Solomon 编码以生成奇偶校验。
  • Turbine 传输：
    这些数据和编码分片随后发送给一小组选定的对等节点，它们进一步传播到“树”的下游。
  • 重新组装：
    如果一个验证者接收到足够的总分片（≥ FEC 集中的数据分片数），它就可以重构整个数据。此重新组装过程高度依赖于 try_recovery() 函数。

UDP vs. QUIC

Solana 目前使用 QUIC 作为区块传播协议，但之前使用的是 UDP。

  • UDP（用户数据报协议）：历史上 Solana 选择 UDP，因为它具有最小的开销——没有握手过程，没有内置的拥堵控制，这对于低延迟的区块传播是有利的。
  • QUIC：是一种运行于 UDP 之上的现代传输层协议，具有拥堵控制、改进的安全性（TLS 1.3）和更强大的错误恢复能力。Solana 切换到 QUIC 的目的是为了处理极高的交易吞吐量，并比原始 UDP 更可靠。

纠删编码机制：从理论到实现

如果你想快速刷新你在纠删编码方面的理论基础，你可以参考这篇文章。

替代方案：简单的复制

如果没有纠删编码，可能需要复制整个区块以确保可靠性。对于大型区块或频繁的传输，这迅速变得不可承受，浪费带宽和网络资源。

多项式插值与 Reed–Solomon

Reed–Solomon 纠删编码将每个数据分片视为一个多项式上的点。只需几个额外的奇偶校验点，即使某些点（数据分片）丢失，也可以重构该多项式。这比原始复制要高效得多，适合部分丢失的恢复。

数据分片 vs. 代码分片

  • 数据分片：包含原始交易数据。
  • 编码分片：使用 Reed–Solomon 代码从数据分片生成。通过收集足够的总分片（数据 + 编码），节点可以恢复任何丢失的数据片段。

代码演练：关键函数

data_shreds_to_coding_shreds()

函数 data_shreds_to_coding_shreds() 将数据分片按其“FEC 集索引”进行分组，并计算要生成多少编码分片：

fn data_shreds_to_coding_shreds(
    keypair: &Keypair,
    data_shreds: &[Shred],
    next_code_index: u32,
    reed_solomon_cache: &ReedSolomonCache,
    process_stats: &mut ProcessShredsStats,
) -> Result<Vec<Shred>, Error> {
    if data_shreds.is_empty() {
        return Ok(Vec::default());
    }
    // 1）按 FEC 集索引对数据分片进行分组
    let chunks: Vec<Vec<&Shred>> = data_shreds
        .iter()
        .group_by(|shred| shred.fec_set_index())
        .into_iter()
        .map(|(_, shreds)| shreds.collect())
        .collect();

    // 2) 对于每个组，确定总的纠删批大小
    let next_code_index: Vec<_> = std::iter::once(next_code_index)
        .chain(chunks.iter().scan(next_code_index, |next_code_index, chunk| {
            let num_data_shreds = chunk.len();
            let is_last_in_slot = chunk.last()
                .copied()
                .map(Shred::last_in_slot)
                .unwrap_or(true);
            let erasure_batch_size = get_erasure_batch_size(num_data_shreds, is_last_in_slot);
            *next_code_index += (erasure_batch_size - num_data_shreds) as u32;
            Some(*next_code_index)
        }))
        .collect();

    // 3) 生成编码分片（可能并行）
    let coding_shreds: Vec<_> = if chunks.len() <= 1 {
        chunks.into_iter()
            .zip(next_code_index)
            .flat_map(|(shreds, next_code_index)| {
                Shredder::generate_coding_shreds(&shreds, next_code_index, reed_solomon_cache)
            })
            .collect()
    } else {
        PAR_THREAD_POOL.install(|| {
            chunks.into_par_iter()
                .zip(next_code_index)
                .flat_map(|(shreds, next_code_index)| {
                    Shredder::generate_coding_shreds(&shreds, next_code_index, reed_solomon_cache)
                })
                .collect()
        })
    };
    Ok(coding_shreds)
}

过程中的关键步骤：

  • 按 FEC 索引对数据分片进行分组。
  • 使用 get_erasure_batch_size() 决定需要多少总分片（数据 + 编码）。
  • 如果存在多个 FEC 集，则并行生成编码分片（通过 Reed–Solomon）。

generate_coding_shreds()

函数 generate_coding_shreds() 是 Reed–Solomon 编码的核心：

pub fn generate_coding_shreds<T: Borrow<Shred>>(
    data: &[T],
    next_code_index: u32,
    reed_solomon_cache: &ReedSolomonCache,
) -> Vec<Shred> {
    // 1）将数据分片转换为原始切片
    let data: Vec<_> = data.iter()
        .map(Borrow::borrow)
        .map(Shred::erasure_shard_as_slice)
        .collect::<Result<_, _>>()?;

    // 2）分配奇偶校验分片
    let mut parity = vec![vec![0u8; data[0].len()]; num_coding];

    // 3）执行 Reed–Solomon 编码
    reed_solomon_cache
        .get(num_data, num_coding)?
        .encode_sep(&data, &mut parity[..])?;

    // 4）将奇偶校验切片包装成编码分片
    ...
}

过程中的关键步骤：

  • 将数据分片转换为原始字节数组。
  • 使用缓存的 Reed–Solomon 实例填充奇偶校验缓冲区。
  • 将奇偶校验缓冲区打包到“编码分片”结构中。

try_recovery()

恢复函数 try_recovery() 在某些数据分片未到达时使用：

pub fn try_recovery(
    shreds: Vec<Shred>,
    reed_solomon_cache: &ReedSolomonCache,
) -> Result<Vec<Shred>, Error> {
    // 1）识别缺失分片
    let mut shards = vec![None; fec_set_size];
    for shred in shreds {
        let idx = shred.erasure_shard_index()?;
        shards[idx] = Some(shred.erasure_shard()?);
    }

    // 2）使用 Reed–Solomon 重构数据
    reed_solomon_cache
        .get(num_data_shreds, num_coding_shreds)?
        .reconstruct_data(&mut shards)?;

    // 3）将恢复的字节转换为数据分片
    ...
}

过程中的关键步骤：

  • 收集现有的分片（数据或编码），缺失的则标记为 None。
  • 调用 reconstruct_data() 来填充缺失的部分。
  • 将恢复的原始字节转换回完整的数据分片对象。

ReedSolomonCache

构建 Reed–Solomon 查找表的成本很高。因此，Solana 会通过实现 ReedSolomonCache 对它们进行缓存，缓存按照 (data_shards, parity_shards)：

pub struct ReedSolomonCache(
    Mutex<LruCache<(usize, usize), Arc<ReedSolomon>>>,
);

这个 LRUCache 避免了对重复的 (data, code) 配置重新计算相同的表。

深入实施：流程图

以下是两个流程图，展示了 Solana 如何将数据编码为分片（“编码流程”）以及如何恢复缺失数据（“解码流程”）。

纠删编码生成（编码流程）

sequenceDiagram
    participant Ledger as 账本条目
    participant S as 分片器
    participant FEC as FEC 分组
    participant RSCache as ReedSolomonCache
    participant RS as ReedSolomon 编码器
    participant CS as 编码分片生成器
    participant Out as 客户端（输出分片）

    Ledger->>S: 提供账本条目
    S->>S: 将账本条目划分为数据分片
    S->>FEC: 按 FEC 集索引对数据分片进行分组
    FEC-->>S: 返回分组的数据分片

    loop 对于每个 FEC 组
        S->>S: 计算纠删批大小（通过 get_erasure_batch_size）
        S->>RSCache: 请求 RS 实例（带数据分片、奇偶校验分片）
        RSCache-->>S: 返回 RS 实例（可能来自缓存）
        S->>RS: 调用 encode_sep（数据分片，分配奇偶校验缓冲区）
        RS-->>S: 返回计算出的奇偶校验分片
        S->>CS: 将奇偶校验分片包装成编码分片（设置正确的头部）
        CS-->>S: 返回 FEC 组的编码分片
    end

    S-->>Out: 返回数据分片和编码分片

流程解释：

  • 分片器将账本条目拆分为固定大小的数据分片。
  • 数据分片按 FEC 索引分组形成“纠删集”。
  • 分片器为每个组计算总的纠删批大小（数据 + 编码）。
  • 请求 Reed–Solomon 实例于 ReedSolomonCache。
  • 计算并将奇偶校验分片包装为“编码分片”。
  • 输出为数据分片集加上相应的编码分片。

纠删编码恢复（恢复流程）

sequenceDiagram
    participant R as 恢复过程
    participant RSCache as ReedSolomonCache
    participant RS as ReedSolomon 解码器
    participant Out as 客户端（恢复的分片）

    R->>R: 收集可用的数据和编码分片（部分数据分片缺失）
    R->>R: 构建分片数组并为缺失的数据分片创建掩码
    R->>RSCache: 请求 RS 实例（使用预期的数据分片和奇偶校验分片）
    RSCache-->>R: 返回 RS 实例
    R->>RS: 调用 reconstruct_data（包含缺失分片的分片数组）
    RS-->>R: 返回恢复的原始分片字节切片
    R->>R: 将恢复的字节切片转换为数据分片对象
    R-->>Out: 提供恢复的数据显示分片

流程解释：

  • 恢复过程收集它拥有的所有分片（可以是数据或编码）。
  • 标记缺失的分片位置。
  • 请求匹配的 Reed–Solomon 实例于缓存。
  • 通过调用 reconstruct_data() 重建缺失的分片。
  • 将恢复的字节重新合成标准的数据分片对象。

这两个图展示了 data_shreds_to_coding_shreds()、generate_coding_shreds() 和 try_recovery() 函数在实践中的相互作用。它们显示了从账本条目 → 数据分片 → 编码分片（编码）和从部分数据分片 + 编码 → 完整数据分片（解码/恢复）的端到端流程。

纠删批大小选择

变量批大小的必要性

虽然 Solana 通常使用 32 数据 : 32 码的安排，但实际上网络会遇到在一个时隙内产生更少或更多数据分片的情况。如果只有 8 个数据分片，应该生成多少编码分片以保持与 32:32 一样的 ~99% 成功概率？

ERASURE_BATCH_SIZE 查找表

Solana 定义了一个小数组，用于将数据分片的数量 d 映射到总的纠删批大小 d + c。这在代码库中在 ERASURE_BATCH_SIZE 中定义。例如：

pub(crate) const ERASURE_BATCH_SIZE: [usize; 33] = [
    0, 18, 20, 22, 23, 25, 27, 28, 30, // 直到 8 个数据
    32, 33, 35, 36, 38, 39, 41, 42,    // 直到 16 个数据
    43, 45, 46, 48, 49, 51, 52, 53,    // 直到 24 个数据
    55, 56, 58, 59, 60, 62, 63, 64,    // 直到 32 个数据
];
  • 索引：数据分片的数量。
  • 值：总的（数据 + 编码）所需以匹配 32:32 的可靠性，通常为 ~65–70% 的每分片成功率。

例如：

  • ERASURE_BATCH_SIZE[1] = 18 → 1 数据 + 17 编码。
  • ERASURE_BATCH_SIZE[8] = 30 → 8 数据 + 22 编码。

基础概率分析

Solana 的参考标准是 32:32 纠删集，因为它通常可以提供 ~99%+ 的区块恢复，如果每个分片具有 ~65% 的成功到达率。

概率表

在这张表中，对每一行（纠删集大小）在不同网络条件下（每个分片的成功率从 1% 到 100%）进行了二项式或组合分析。表中显示：

  • 行：不同（数据、编码、总）。
  • 列：每个分片到达的概率（1%、5%、10%、等）。
  • 单元格：整个纠删集可以恢复的总体概率。

这是代码确保较小部分集（如 1 数据分片或 8 数据分片）在成功概率上与 32:32 可比较的方式。一旦每分片的成功概率达到 ~70%，基本上所有这些集都超过 99% 的成功概率。

表格的导出方式

  • 标准（32:32）参考点
    Solana 工程师将 32:32 视为“黄金标准”，因为它在单个分片至少有 65% 的成功到达机率时，能够提供约 99% 的恢复概率。

  • 二项式（或组合）分析
    每个分片的到达概率（大致）独立，概率为 $p$。对于大小为 $N = (\text{data} + \text{code})$ 的纠删集，你最多可以丢失 $\text{code}$ 个分片且仍可恢复。成功完全恢复的概率可以通过二项分布计算：

    $$ \Pr(\text{recover}) \;=\; \sum_{k=0}^{\text{code}} \binom{N}{k} \, p^{(N-k)} \, (1-p)^{k}. $$

    Solana 的表格或脚本测试了数据分片与编码分片的不同排列，直到找到能达到与 32:32 相同目标成功概率的组合。

  • 每个数据计数的查找
    工程团队建立的表格指出：“给定 $d$ 数据分片，需要多少总分片 $N$ 以确保在常见的分片成功率（≥65%）下，成功的机率至少为 99%？”该表中的每一行都存储在 ERASURE_BATCH_SIZE[d] 中。

实际使用

每当分片器看到 d 个数据分片在部分批中时，它就执行：

let erasure_batch_size = ERASURE_BATCH_SIZE[d];
let num_coding_shreds = erasure_batch_size - d;

因此，如果产生的数据分片较少，则会生产更高比例的编码分片——维持整体可靠性。

ERASURE_BATCH_SIZE 数组仅选择最小的 (data+code) 总数，当每分片成功率约为 65–70% 时，确保至少达到或超过 32:32 的可靠性曲线。

对性能与挑战的几点评论

性能

带宽效率

  • 简单的方式：重新发送整个区块对诸如 Solana 这样的区块链来说不可扩展。
  • Reed–Solomon 编码：通常增加约 50% 的开销（例如，32:32），如果每个分片至少具有 ~65% 的到达机会，则实现约 ~99% 的成功，这是相对于原始复用而言显著的带宽节省，因为你仅需每个 FEC 集传输奇偶校验数据一次，而不是多次复制整个数据集。

延迟基准

  • Turbine 传播：通常每个分片需 ~2-3 次跳跃，导致全球簇所需总计 ~100–200 毫秒的区块传播时间。这意味着 Solana 能以低于一秒的速度完成区块的确认，同时将数据分发给所有的验证者。
  • 与以太坊的比较：以太坊基于八卦的方式（DevP2P）简化了泛洪，但需要 ~12 秒的区块时间。Solana 通过短时隙（~400 ms）与基于 Turbine 的树形分发的结合，被量身定制用于快速最终确认。

存储优化

  • Blockstore 压缩和索引分片以实现本地存储。这是必不可少的，因为 Solana 的交易速率很高——原始数据增长极快。
  • 历史数据可以通过外部存档，例如果、Filecoin 或专用归档节点，以减轻款项的链上存储对验证者的负担。

Solana 与以太坊

指标 Solana 以太坊
区块时间 ~400 ms ~12 秒
传播协议 Turbine + Reed–Solomon 纠删编码 八卦（DevP2P）
带宽 ~1 Gbps 峰值（突发性，而非连续） ~25 Mbps
数据恢复 通常使用 32:32 FEC + 如有必要则为部分请求 主要依赖于重新发送

Turbine 与 Celestia 的 DAS

  • Turbine：通过分布式整个区块数据，结合纠删编码，以确保每个验证者都有或可以重构完整数据。
  • Celestia：使用数据可用性抽样（DAS），使轻客户端在不存储全部数据的情况下就可以确认数据可用性。Solana 的方法更为整体，但适合其极高吞吐量和快速确认的设计目标。

未来方向

  • 自适应纠删编码

    • 根据实时网络情况动态调整数据/编码比率（例如，32:48）。这可以进一步优化在高数据包丢失或连接不良的情况下的可靠性。

  • 轻客户端支持

    • 潜在地采用类似于 Celestia 的数据可用性抽样，以允许特定轻客户端在不保存所有交易数据的情况下验证链状态。

  • Firedancer 优化

    • Firedancer 项目的目标是通过进一步的并行化在 Turbine 和 I/O 层实现 10 Gbps 的吞吐量，推动实时区块传播的极限。这可能包括利用先进的 NIC 特性、GPU 加速或更高效的并发处理。

结论

Solana 的 Reed–Solomon 纠删编码是其高性能设计的重要特性，允许：

  • 通过 Turbine 快速数据传播，
  • 即使在数据或数据包丢失时也能进行稳健恢复，
  • 不同的批大小保持 ~99% 成功概率，适应变化的网络条件。

通过将这些编码策略与 Merkle 证明、签名和一个精心设计的 Reed–Solomon 表缓存结合起来，Solana 在不牺牲可靠性的情况下保持极高的吞吐量。无论你是在处理标准的 32:32 还是较小的部分集，纠删编码确保你的区块数据仍然是可恢复的——即使网络并不完美。

参考文献

  • 原文链接： github.com/thogiti/thogi...
  • 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
thogiti
thogiti
https://thogiti.github.io/

thogiti

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！