如何在不被 REKT 的情况下优化你的Gas消耗 第二部分

在这篇文章中（如何在不被 REKT 的情况下优化你的Gas消耗 的续集），我们将关注于 Solidity/Yul 库，这些库实现了 DeFi 世界核心的数学和经济计算，并解释了为什么等价性检查是开发者和审计员在处理这类代码时的一个强大工具。

我们的计划是：

1. 我们讨论算术漏洞及由此导致的对 DeFi 协议的经济攻击，以 常数函数做市商（CFMM） 的分类作为激励示例。

2. 我们详细检查一些最近的案例，并解释 Certora 发现的 PRBMath 库的舍入错误。

3. 我们展示如何使用简单的 3 行“等价规范”来检测该漏洞，并证明其修正是无错误的。

注意： 由于这是本系列的第二部分，我们将自由使用在上一篇博客文章中讨论的等价性检查、形式验证、Certora Prover 和 Certora Verification Language (CVL) 的术语。你可以通过阅读第一部分来刷新你的记忆：第一部分。

自动做市商（AMM）的速成课程

一个 分布式金融（或 DeFi）应用程序 是一个基于规则的金融系统，按照通过一个（或多个）区块链上智能合约实现的协议运行。DeFi 应用程序的一个重要类别是 去中心化交易所（或 DEX）。这些交易所被定义为用户（称为 交易者）可以以非托管的方式（即，无需中介 参与者 来促进资金的转移和托管，但可能需要中介智能合约的帮助）交换加密货币的市场。

与传统（或甚至中心化的加密）交易所不同，这些交易所通常依赖于 订单簿模型 或 指定做市商 提供 流动性，大多数 DEX 依赖于一种称为 自动做市商（ AMM）的协议类别。

每个 AMM 的核心是一个 流动性池 的集合。每个流动性池对应一对可互换的加密资产（或代币），我们在下面的图中将其表示为代币 A 和代币 B。

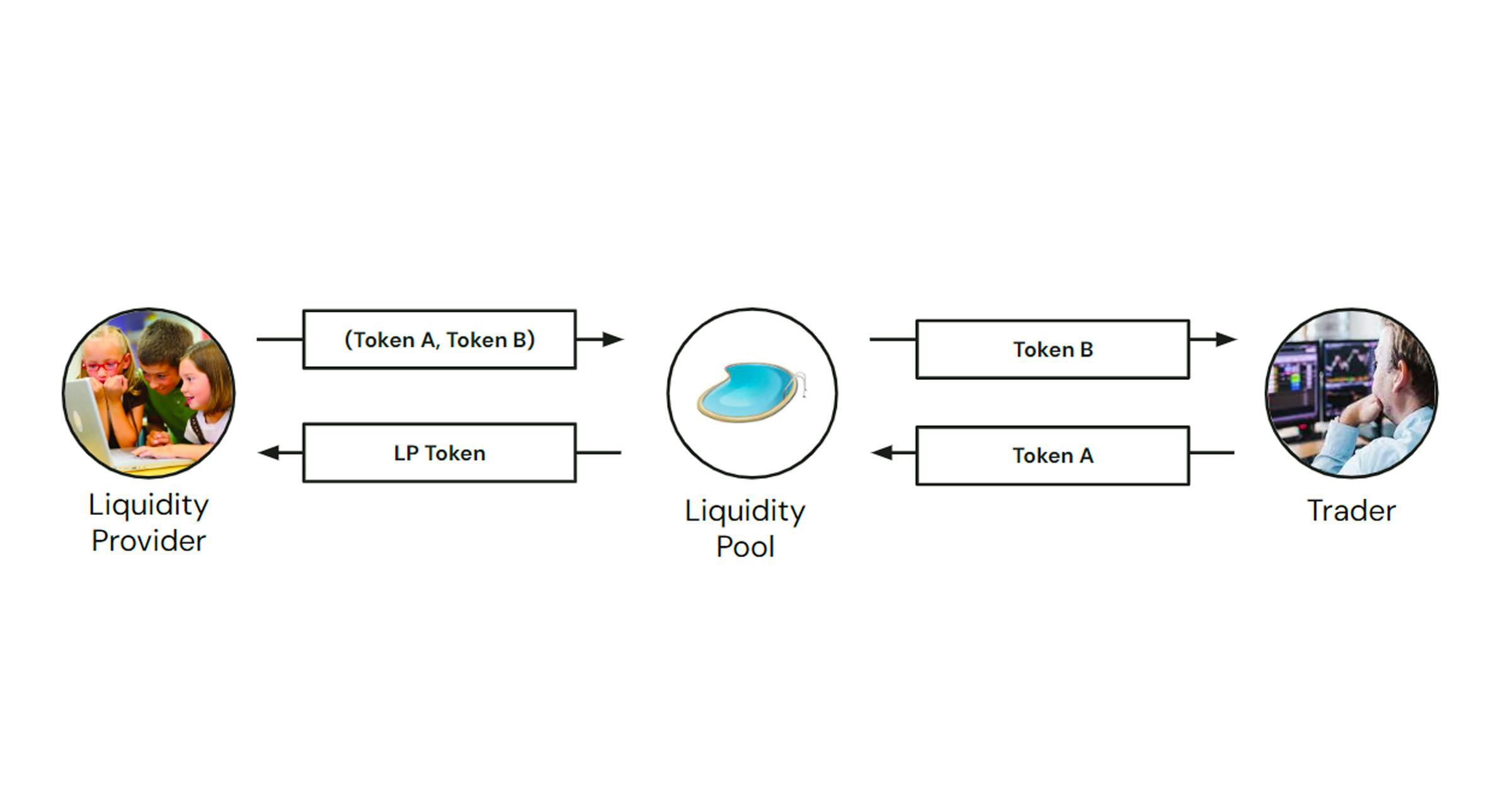
用户将一定数量的每种代币存入池中，称为 流动性提供者（或简称 LP）。作为对其投资的回报，他们获得一个流动性代币，该代币本质上作为 仓库收据，记录其相对于当前池中存入的代币 A 和代币 B 的余额的投资价值。

与订单簿（一个用于匹配买家和卖家的点对点协议）不同，AMM 实施了一种池对用户的方法，其中每个希望用一定数量的代币 A 交换代币 B 的用户都与池本身进行交互。通过这种方式，交易者可以立即获得流动性，而无需等待对手方，同时 LP 由于池积累的交易手续费而获得投资利润。

常数函数做市商（CFMM）和交易不变量

正如你可能注意到的，我们上述描述中有一个非常重要的细节被忽略了。

问题： 假设一个交易者希望 交换 1000 个 A 代币，AMM 如何确切知道要发送多少 B 代币？

关键点是 AMM 不需要访问外部定价信息源（例如，定价预言机），因为每个市场本质上都是一个 价格发现机制。

从数学角度来看，几乎所有现有的 AMM 都属于一个称为常数函数做市商（CFMM）的类别。这意味着它的交易（或“交换”）行为是由一个单一函数所决定的。

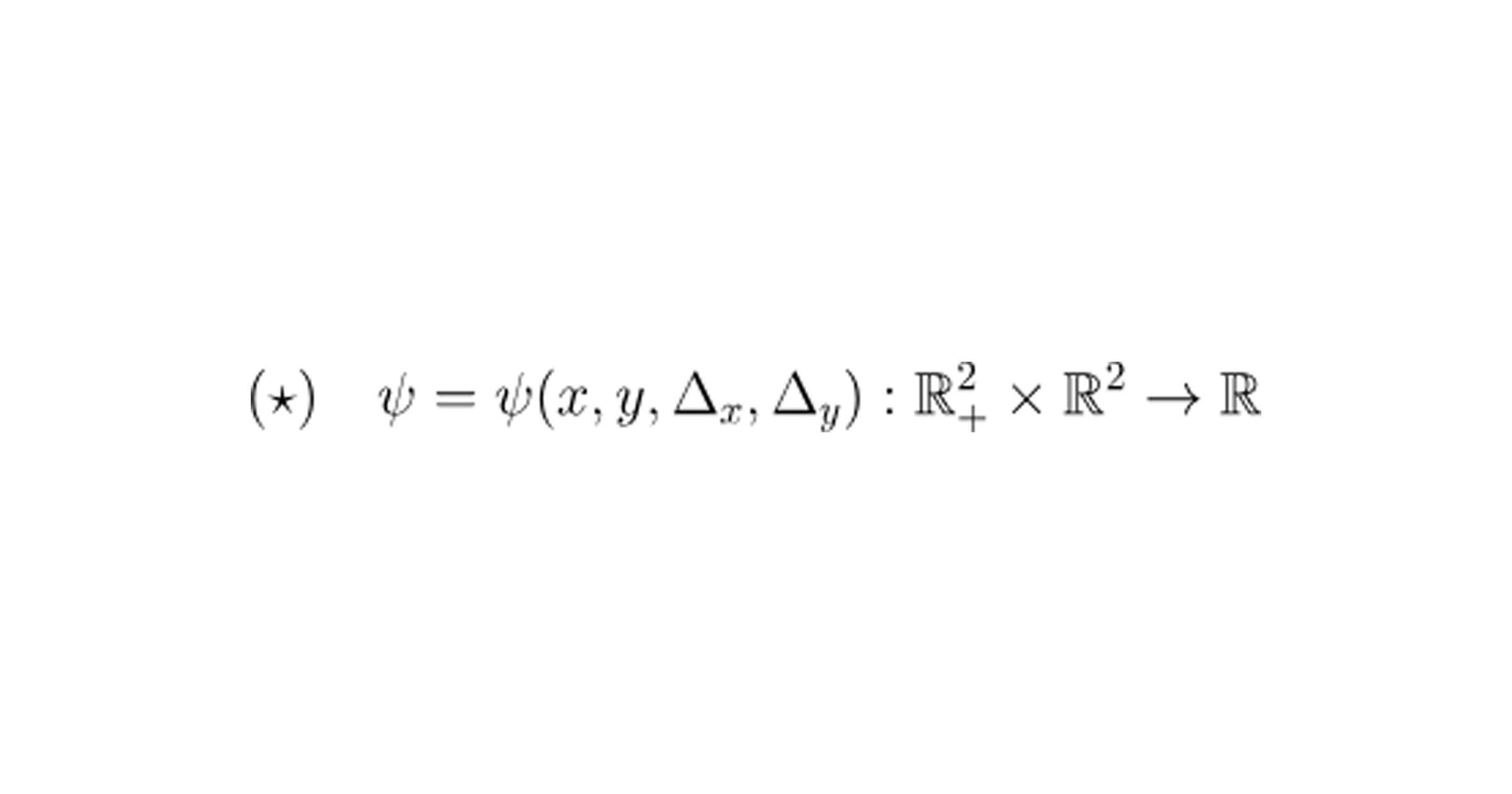
其输入为：

AMM 仅当认为交易报价对其是 有利 的时候才会接受交易。在具体术语上，这意味着 AMM 应该仅当不等式成立时才能接受交易。

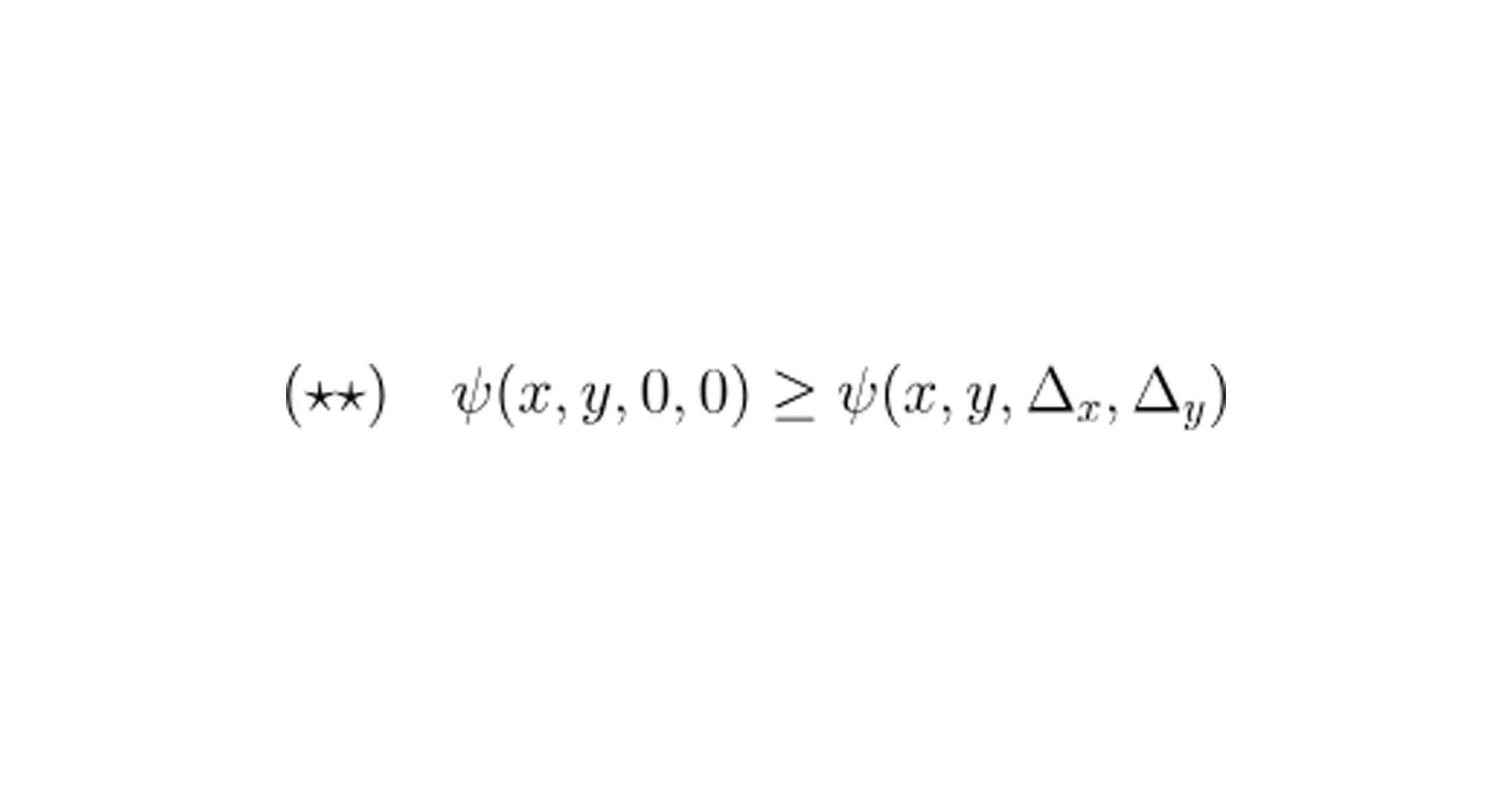
示例：

常数乘积做市商：这是最经典的案例，由马丁·科佩尔曼（Martin Koppelmann）和维塔利克·布特林（Vitalik Buterin）在 2018 年提出，并首次由 Uniswap 在 2018 年实施。该 CFMM 的交易函数（★）为

展开这个公式，我们发现如果我们用常见的符号来表示两个储备的乘积 k := x*y，那么不等式 (★★) 精确地说明 k 必须在每笔交易中保持非递减，这是常数乘积 AMM 的一个众所周知的不变量。

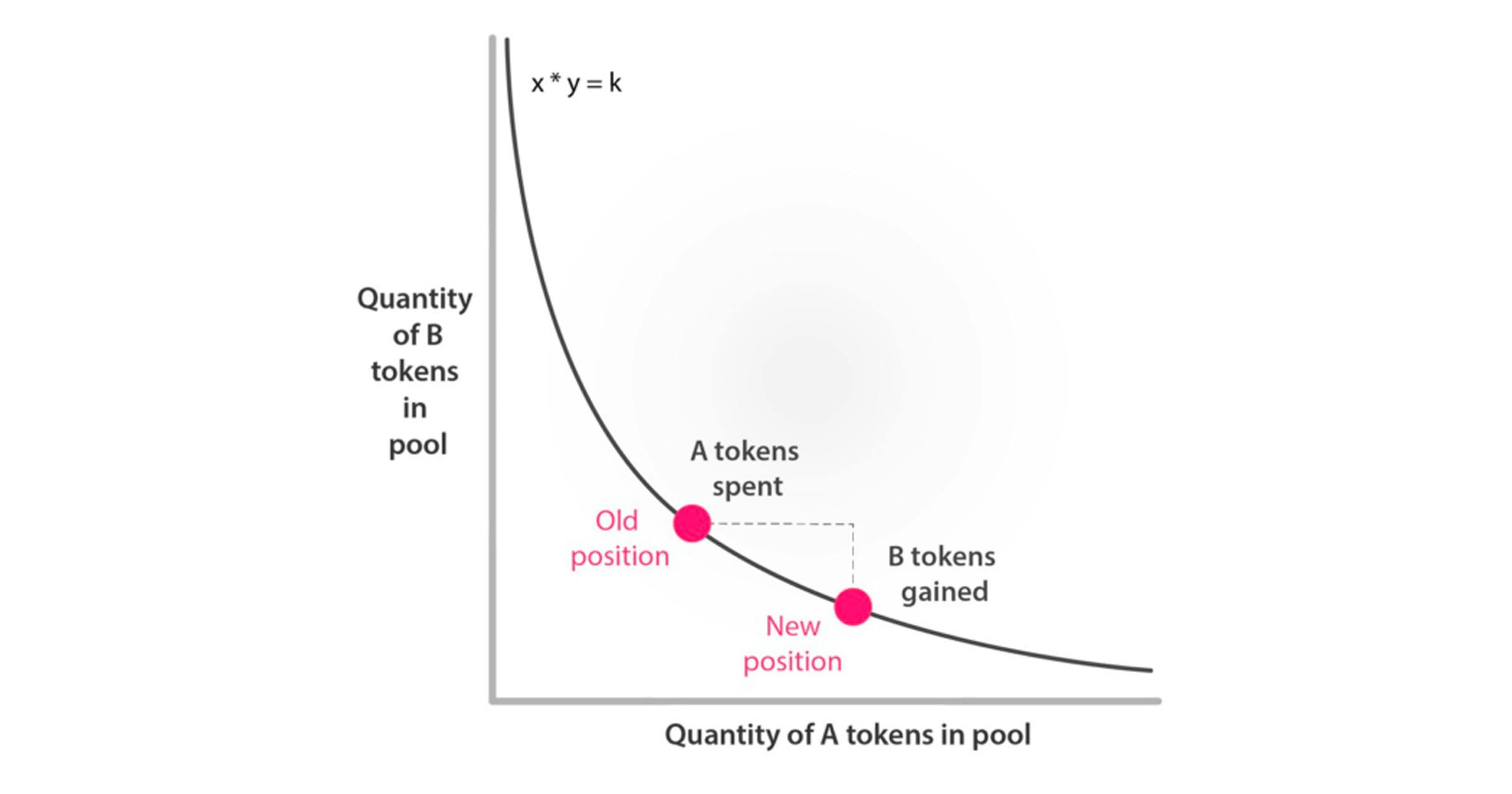
我们想强调的是，没有什么神奇之处在于 x*y = k 的公式！还有许多其他类型的交易函数，其中一些相当复杂的数学。

这并不令人惊讶：当预期的用例不同（例如，稳定币、衍生品、某些类型的合成资产）时，CFMM 不变量的设计应该反映这一点，因为不同的交易函数优化本质代币对的不同属性。

利用交易函数

问题： 如果由于算术错误或实现错误，用户能够以违反不等式 (★★) 的方式与 AMM 的智能合约交互，会发生什么？

在这种情况下，攻击者可以迫使 AMM 持续执行 不利 的交易，从而消耗流动性提供者 (LP) 存入池中的资金。

这种攻击交易非常微妙：每个流动性提供者持有的 LP 代币的数量在每次攻击前后保持不变。然而，利用这种缺陷使攻击者能够 蚕食他们的价值。一个粗略但有用的类比是通货膨胀：流动性提供者仍然持有相同数量的现金（LP-Tokens），但现在相同数量的现金可以买到的商品（A 或 B 代币）少得多。

最近的此类攻击案例包括：

• Alpha Homora 漏洞（2021年2月）
• Solana 程序库中的 spl-token-lending 错误（2021年12月）
• Yieldly HDL 分配池 漏洞（2022年3月）
• Hundred Finance 漏洞（2023年4月）
• Midas Capital 漏洞（2023年6月）

这种算术错误中最常见的类型可能是计算交易函数时的离一错误，即错误地将结果四舍五入了方向¹。

漏洞描述

备注： 如我们在披露中所述，我们发现的舍入错误出现在多个版本的 PRBMath 库中。为了方便起见，在本节中我们将始终提到提交 e2fc29127c（v4.0）。

大致而言，PRBMath 库的 Common.sol 函数

function mulDiv(uint256 x, uint256 y, uint256 denominator) pure returns (uint256 result)
/// @notice 以完全精度计算 floor(x*y÷denominator).
/// 需求：
/// - 分母不能为零。 
/// - 结果必须适合 uint256。

实现了以下算法（致谢：Remco Bloemen）以高效计算_无符号_乘法和除法：

1. 使用中国剩余定理（CRT）获取一个 512 位的分子表示为两个 uint256 变量的有序对 (prod1, prod0)（有关解释，请参阅 Remco 的 中国剩余定理 和 完整乘法 文章）：

uint256 prod0; // 最低有效的 256 位
uint256 prod1; // 最高有效的 256 位
assembly ("memory-safe") {
    let mm := mulmod(x, y, not(0))
    prod0 := mul(x, y)
    prod1 := sub(sub(mm, prod0), lt(mm, prod0))
} // product = prod1 * 2^256 + prod0.

2. 通过从 (prod1, prod0) 中减去余数，使除法精确：

uint256 remainder;
assembly ("memory-safe") {
    // 使用 mulmod Yul 指令计算余数。
    remainder := mulmod(x, y, denominator)
    // 从 512 位数字中减去 256 位数字。
    prod1 := sub(prod1, gt(remainder, prod0))
    prod0 := sub(prod0, remainder)
}

3. 计算分母的最大 2 次幂因子（LPOTD）并进行除法（请参阅 Remco 的文章和 StackExchange 问题 的解释）：

uint256 lpotdod = denominator & (~denominator + 1);
uint256 flippedLpotdod;

assembly ("memory-safe") {
    // 从分母中提取 2 的幂因子。
    denominator := div(denominator, lpotdod)

    // 将 [prod1 prod0] 除以 lpotdod。
    prod0 := div(prod0, lpotdod)
    flippedLpotdod := add(div(sub(0, lpotdod), lpotdod), 1)
}

// 将 bits 从 prod1 移入 prod0。
prod0 |= prod1 * flippedLpotdod;

4. 使用牛顿-拉夫森迭代法对分母进行反转 mod 2²⁵⁶。（详见 帖子和 论文 的初始猜测；注意：由于 亨塞尔的提升引理，这在有限域中有效）：

uint256 inverse = (3 * denominator) ^ 2; // inverse mod 2^4
inverse *= 2 - denominator * inverse; // inverse mod 2^8
inverse *= 2 - denominator * inverse; // inverse mod 2^16
inverse *= 2 - denominator * inverse; // inverse mod 2^32
inverse *= 2 - denominator * inverse; // inverse mod 2^64
inverse *= 2 - denominator * inverse; // inverse mod 2^128
inverse *= 2 - denominator * inverse; // inverse mod 2^256

5. 我们现在可以通过将 prod0 与分母的模反转相乘进行除法：

result = prod0 * inverse;

这将产生我们所需的结果。

了解这一点后，我们现在可以回顾如何实现 有符号 乘法和除法，该过程在 Common.sol 函数中：

function mulDivSigned(int256 x, int256 y, int256 denominator) pure returns (int256 result)
/// @notice 以完全精度计算 floor(x*y÷denominator).
/// 需求：
/// - 请参见 {mulDiv} 中的要求。
/// - 输入不能为 `type(int256).min`。
/// - 结果必须适合 int256。
///
/// @param x 作为 int256 的乘数。
/// @param y 作为 int256 的乘法器。
/// @param denominator 作为 int256 的除数。
/// @return result 作为 int256 的结果。

它是基于先前提到的计算，实施以下算法：

1. 提取输入的绝对值：

uint256 xAbs;
uint256 yAbs;
uint256 dAbs;
unchecked {
    xAbs = x < 0 ? uint256(-x) : uint256(x);
    yAbs = y < 0 ? uint256(-y) : uint256(y);
    dAbs = denominator < 0 ? uint256(-denominator) : uint256(denominator);
}

2. 通过简化为无符号情况（即，在输入的绝对值上调用先前提到的无符号 乘法和除法 函数）来计算结果的绝对值：

uint256 resultAbs = mulDiv(xAbs, yAbs, dAbs);

3. 如果结果的绝对值无法适合 int256-variable，则使用自定义错误回退：

if (resultAbs > uint256(type(int256).max)) {
    revert PRBMath_MulDivSigned_Overflow(x, y);
}

4. 有效地计算每个输入的符号：

uint256 sx;
uint256 sy;
uint256 sd;
assembly ("memory-safe") {
    // "sgt" 是“有符号大于”汇编指令，"sub(0,1)" 是二进制补码中的 -1。
    sx := sgt(x, sub(0, 1))
    sy := sgt(y, sub(0, 1))
    sd := sgt(denominator, sub(0, 1))
}

5. 通过取 XOR 计算整体符号并返回结果：

// 对 sx, sy 和 sd 进行 XOR。这样做是检查输入中是否存在 1 或 3 个负号。如果存在，结果应为负；否则，结果应该为正。
unchecked {
    result = sx ^ sy ^ sd == 0 ? -int256(resultAbs) : int256(resultAbs);
}

问题是 mulDivSigned 算法的步骤 2 是错误的，因为

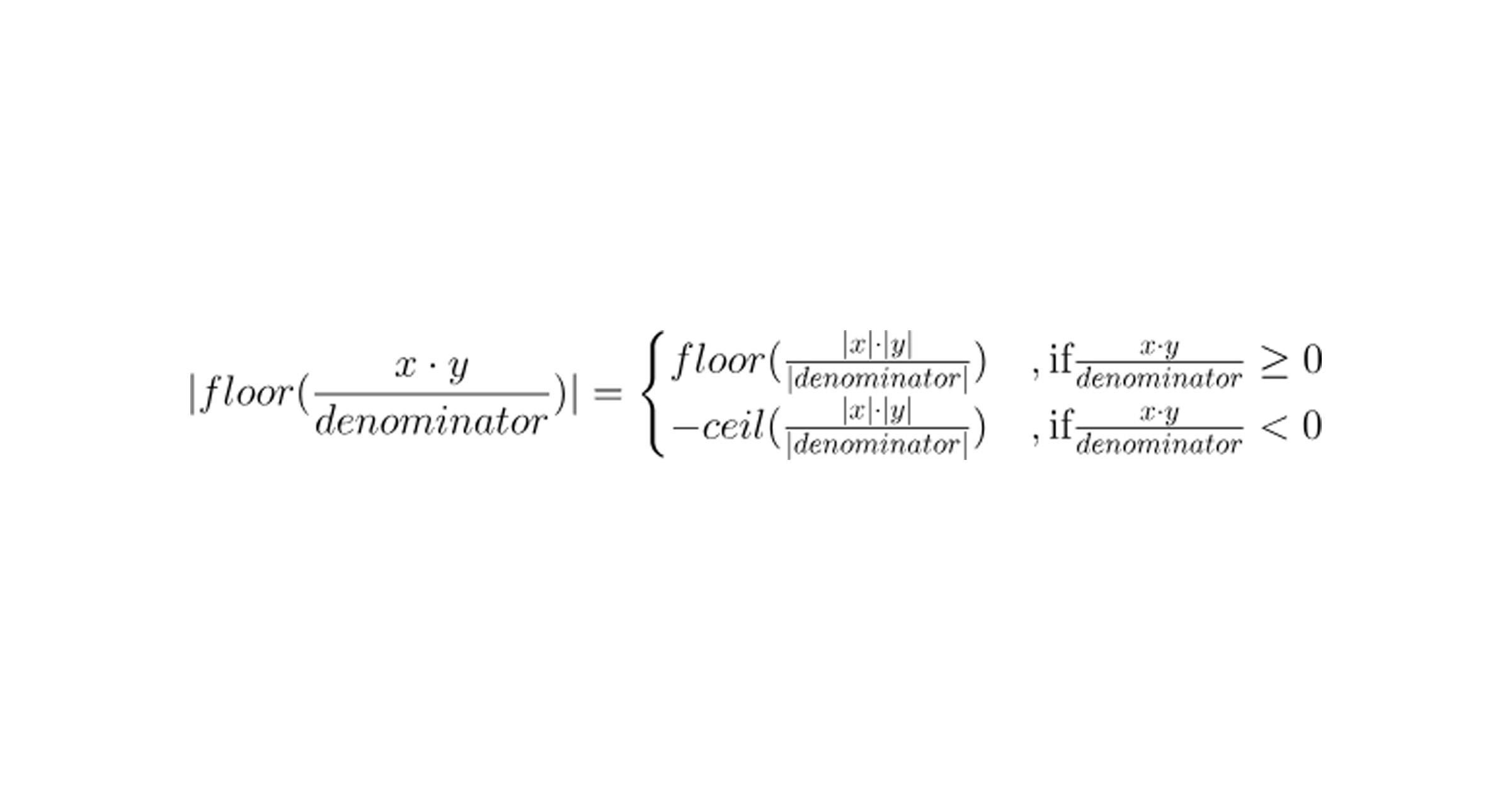
因此，无论何时结果为负，我们实际上是朝零进行舍入，而不是朝负无穷，导致了一个离一错误。

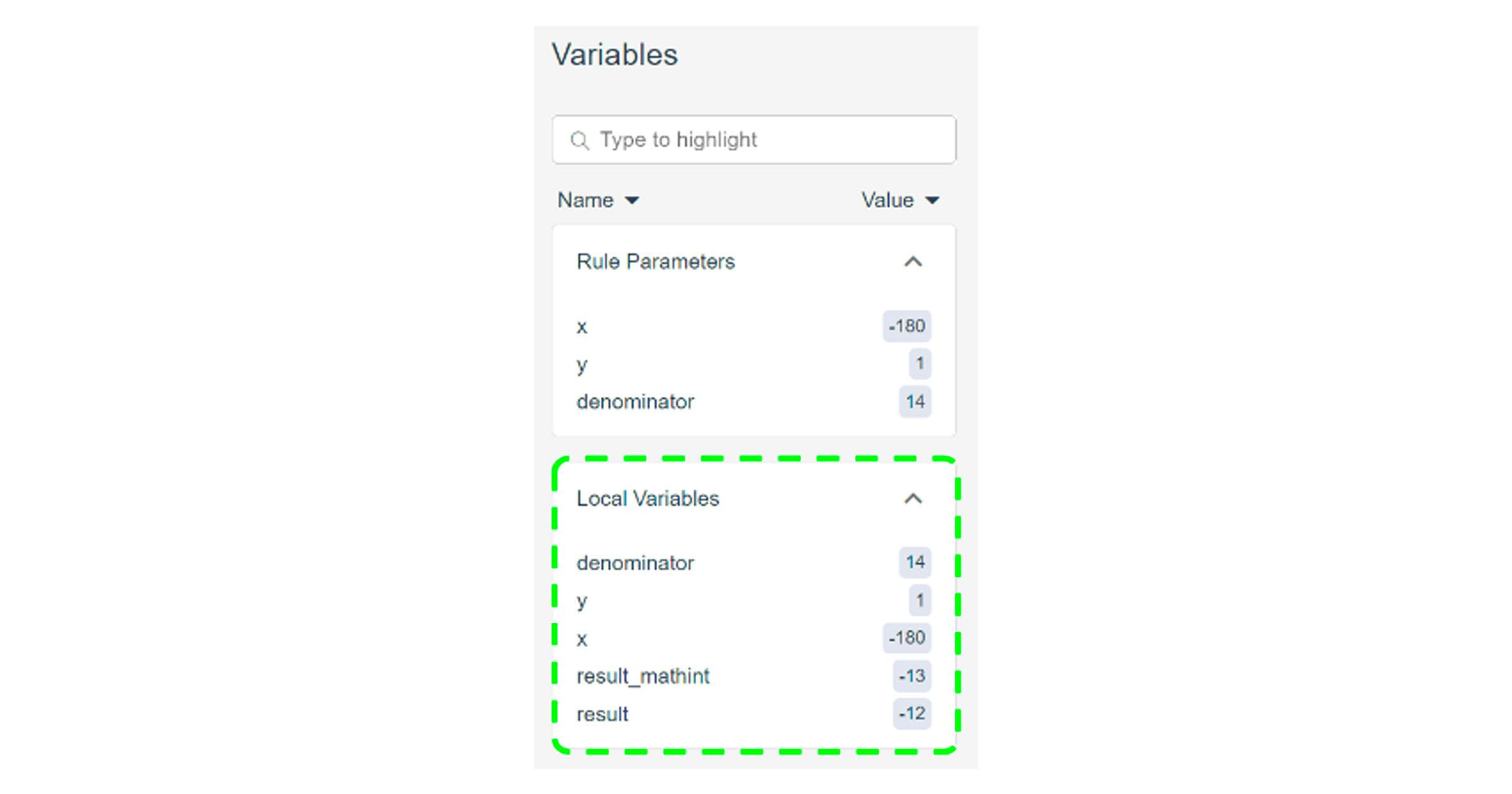
示例： 取

(x,y,denominator) = (-180,1,14)

然后：

(xAbs,yAbs,dAbs) = (180,1,14)
(sx,sy,sd) = (1,0,0)

因此：

resultAbs = mulDiv(180, 1, 14) = floor(12.857…) = 12
result = -12

但：

floor(-12.857) = -13 ≠ result

等价性检查和简单规范

一般来说，编写形式规范是一项艰巨的工作。然而，对于计算库，所需行为很容易通过数学来描述，因为规范几乎可以自我编写。考虑我们在前一节中讨论的两个 PRBMath 函数。

仅通过查看该函数的 NatSpec 注释，我们就可以为 mulDivSigned 生成一个规范：

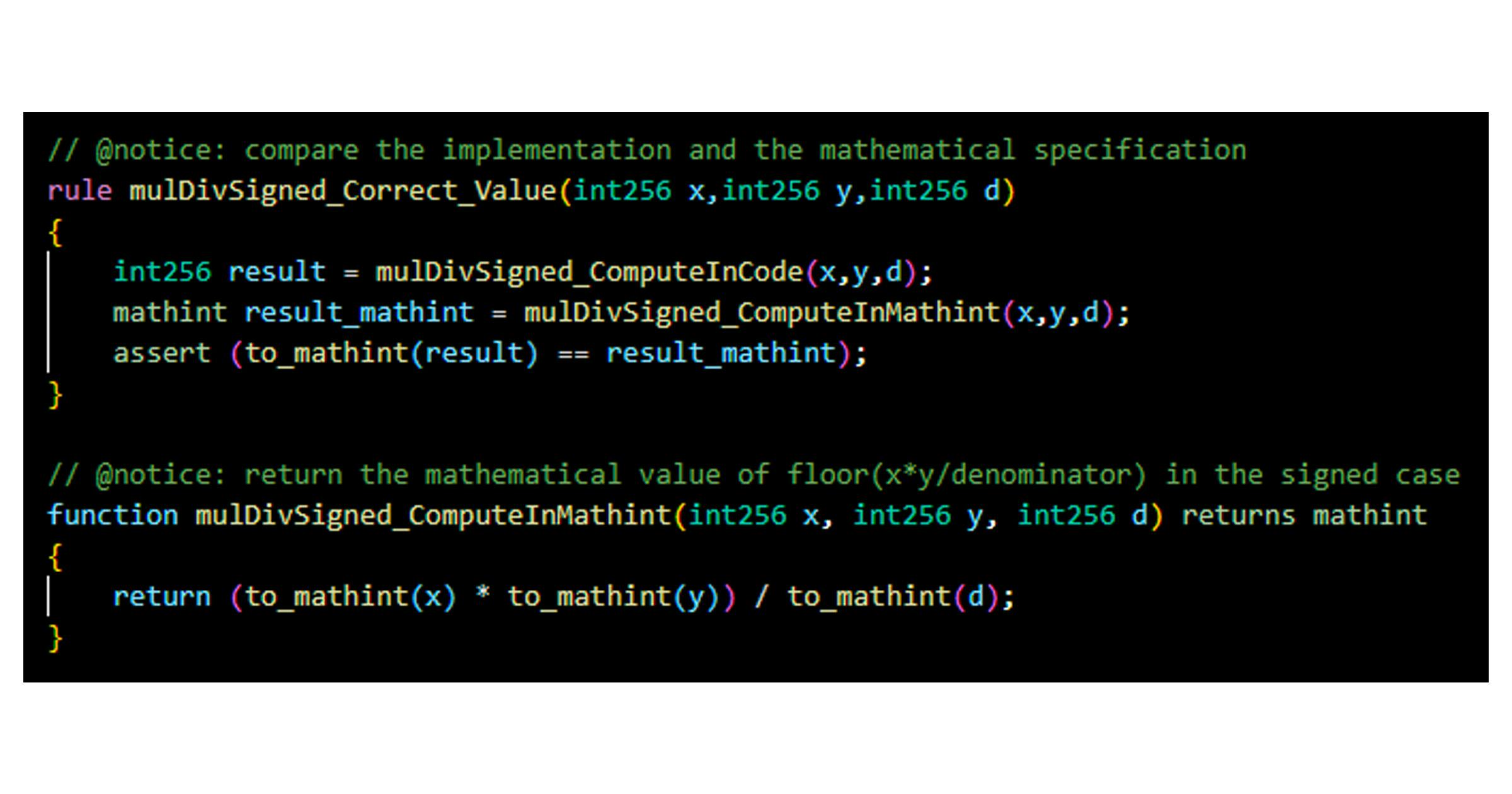
将这个 规范² 通过 Certora Prover 运行，会产生反例，表明 mulDivSigned 存在离一错误：

这就是整个秘密。我们甚至不需要阅读代码或理解 mulDivSigned（或 mulDiv）是如何实现的。

结论

数学库是 DeFi 生态系统的基本组成部分。然而，让它们正确运行惊人地困难（尤其是在激进优化他们的Gas消耗时），并且审计它们可能是乏味而困难的。

上述错误证明了 Certora 的等价性检查器和 CVL 语言的表达能力的重要性：一个基本的 CVL 规范（一个“等价规范”）可以发现数学库的 Solidity 代码中的错误，而这些库涉及大量的 Yul 代码段、众多的位操作技巧，甚至还有一点数论的内容——

所有这些都无需了解实现的任何细节！

¹ 尽管我们到目前为止的所有讨论都在 AMM 基于 DEX 的上下文中进行，但我们至少应该提到这个问题也出现在其他 DeFi 应用中。例如，在借贷平台的情况下，已在 ERC-4626（在“安全考虑”下）中指出：“…… 金库实现者应该意识到， across various view methods …… ”中存在使用特定的 相反舍入方向 的需求。然而，为了简化起见，我们选择了专注于一种 DeFi 应用程序的类别，而不是将这种类型的漏洞进行全面分类。

² 在 第一部分中使用的术语中，生成该规范是等价性检查器的“第二模式”，该模式将 Solidity 或 Yul 代码与用 Certora Verification Language (CVL) 编写的逻辑表达式进行比较。我们这里只生成了半个等价规范，因为我们不需要关心回退条件。

• 原文链接： certora.com/blog/rekt-pa...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～