关于协作式 zk-SNARKs 的简要说明

这是我在2024年入住Antalpha实验室清迈黑客之家期间，针对论文分享会的阅读笔记和准备。特别感谢于国博士、PinHao、Gunit对论文理解的讨论，以及每位在黑客之家的人💛，还有来自TEM的评审们！

zkSNARKs 很有帮助，因为它们是通用的且保护隐私。然而，主要的限制在于只有拥有见证的单方才能编译证明。这一限制使得 zkSNARKs 无法应用于需要多个各自拥有秘密的各方共同生成证明的某些场景。

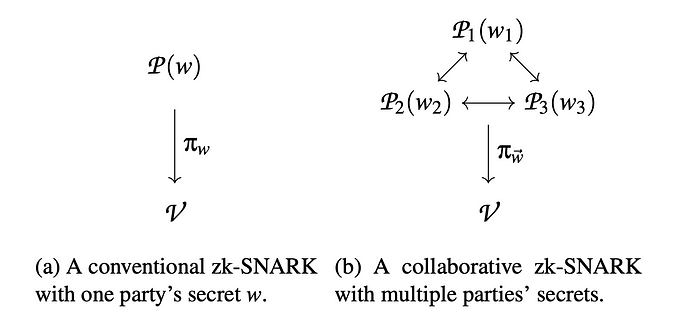
来自论文 Experimenting with Collaborative zk-SNARKs: Zero-Knowledge Proofs for Distributed Secrets 的传统和协作 zk-SNARKs

如果存在一个解决方案，我们可以通过多方计算 zk-SNARK 证明，那会怎么样呢？这将使某些有用的应用成为可能：

1. 外包 ZKP 计算：

想象一下使用你的手机进行计算密集型 ZKP。一个解决方案是共享秘密，让其他服务器为你计算，但我们不希望这样，因为秘密将不再是秘密。相反，我们可以使用 coSNARK，将秘密分成几部分，发送到不同的服务器，让这些服务器为你计算结果，而它们都无法知道整体秘密。

2. 来自协作证明的公共可审计 MPC：

将 MPC 和 ZKP 结合的核心特性之一是 MPC 计算的可验证性。该结合扩展了安全 MPC，生成能够单独检查计算正确性的证明，消除了审计参与的需求。

有关更多用例，我建议查看 Taceo 的文档。

为了使 coSNARK 成为可能，一个简单的想法是“对证明者进行 MPC”。MPC 代表多方计算，它将处理一个函数以计算输出和来自多方的输入，而参与者无法了解到其他方的输入。虽然这可以工作，但在实践中如果我们将 zk-SNARK 计算作为普遍用途 MPC 中的函数进行计算，则效率较低。zkSNARK 证明生成大约比验证慢 1000 倍，MPC 本身也大约比基本计算慢 1000 倍。对证明者进行 MPC 将引入 1,000,000 倍的减速。本文的研究目标是找到一种解决方案，使减速限制在仅 1,000x ~ 2,000x 范围内。

coSNARK

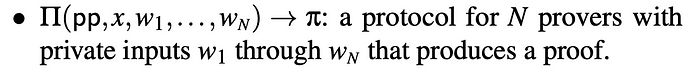
coSNARK 中的证明步骤

coSNARK 的定义类似于我们在传统 zkSNARK 中的定义，证明步骤则分布到多个证明者。

现在我们知道我们的目标是以某种方式结合 MPC 和 zkSNARK，我们该怎么做呢？策略如下：

• 选择合适的 MPC 方案 — SPDZ 和 GSZ
• 针对多个证明者对 zkSNARK 方案进行概括
• 优化

选择合适的 MPC 方案 — SPDZ 和 GSZ

SPDZ 是一个不诚实多数的 MPC 协议，GSZ 是一个诚实多数的 MPC 协议，两者都是线性秘密共享方案。SPDZ 采用加性秘密共享，而 GSZ 使用夏密尔秘密共享。前面的论文表明，SPDZ 可以在椭圆曲线组上运行，GSZ 也是如此，因为它在底层使用夏密尔秘密共享。直接在椭圆曲线组上运行，相比于在基础域上计算，大大降低了通信成本。在我看来，线性秘密共享 + 在椭圆曲线组上运行的能力使这两种 MPC 方案成为 coSNARK 的良好选择。

针对多个证明者的概括 zkSNARKs

zkSNARKs 中有许多构建块，这里我们想解决的是针对多项式评论的 MPC 协议。我们在这里利用来自线性共享方案的线性重构能力，这意味着每方能够单独计算他们的份额并进行证明，然后将它们组合在一起作为有效的承诺或证明。

以 KZG 为例：

由于函数已经被共享，问题出现在承诺和证明阶段，操作在设置和检查时保持不变。论文认为，承诺和证明阶段的线性重构将使多方能够各自计算自己的部分，并且仍然是正确和安全的。

优化

现在我们看一下如何通过查看 zkSNARK 中的各个“部件”来优化计算。论文包含了其他证明方案，在这里我将重点介绍 plonk 以便更容易理解。FFT、MSM、多项式除法和乘积检查是主要的部件，我们将逐一讨论它们。

FFT 和 MSM 是线性操作，在 MPC 风格中，每方可以在本地计算他们的份额而无需通讯，然后再将它们合并，这令人兴奋，因为在 MPC 风格中，传统瓶颈不会带来额外的开销。

多项式除法 是一个非线性且复杂的操作，然而在大多数 snark 例如 KZG 中，我们将使用公共值来构造要被除的多项式，因为这不会因不同的见证输入份额而改变，这在 MPC 方式中不会引入更多的开销。

最后 乘积检查， 要对所有方进行乘积检查，我们需要将每个个体的所有 n 份份额相乘，天真地说，这可能需要 n-1轮通讯，通过使用 Barr-Ilan 和 Beaver 提出的一个技巧，我们可以将乘积检查过程并行化，使通讯成本保持为常数。高层次的想法是，参与方就一组共享的随机数达成一致，参与方用这些随机数及最后一个随机数的逆加密他们的部分，在结合加密后的部分时，随机数会随着第一个随机数和最后一个随机数的逆相抵消。

以 MPC 方式计算乘积检查的步骤

性能

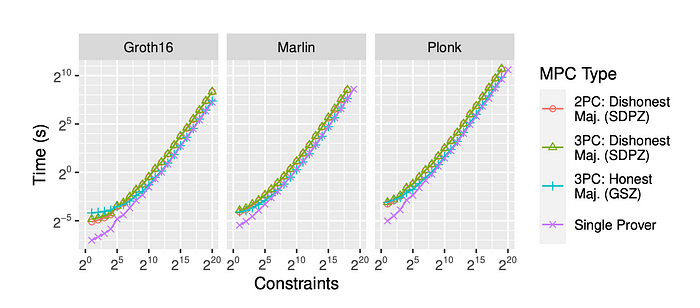
不同方和协议下的证明时间，基于 3 千兆比特的连接。NPC 意味着 N 个证明者之间的合作。一个不诚实多数 (SPDZ) 协议在私密性上是安全的。

实验中的性能令人兴奋，使用 GSZ（诚实多数）的方案几乎能够实现与单一证明者相同的运行时间，而对于 SPDZ（不诚实多数），方案仅引入 2 倍的减缓，从这个意义上说，能够容忍单一证明者运行时间的应用也应该能够使用多个证明者，并且 coSNARKs 是实用的。

当约束大小较小时，多证明者方法较慢，因为网络通信成本占主导地位。由于通讯次数在约束中是次线性的，当约束较大时，多证明者的方法表现得相当好。

诚实多数证明者（GSZ）的运行时间基本上与单一证明者相同，而 SPDZ 导致的 2 倍运行时间增加来自于 SPDZ 在协议中使用消息认证码 (MAC)，从高层看，使用 SPDZ 计算我们需要在消息本身和 MAC 上进行操作，导致了 2 倍的计算开销。

结束语

我第一次在 ZK 播客中听到 coSNARK，对它是如何在底层工作的产生了好奇。这篇论文对于 ZKP 的入门者（比如我）也很不错，因为它广泛覆盖了不同 ZKP 方案、所用的部件以及 MPC 的主题。没有包含太多数学，是一个很好的学习来源，可以使人对整个领域的概念有一个大致的了解。

对于一些最近的突破，Taceo、cursive 和 PSE 合作发布了 coSNARK alphanet，这篇 博客 介绍了高层设计和流程！我认为这是一篇不错的文章，看看 coSNARKs 是如何在现实生活中被使用的。

参考文献

• Experimenting with Collaborative zk-SNARKs: Zero-Knowledge Proofs for Distributed Secrets
• coSNARK 实现 by Alex
• Alex 的演讲
• 来自 TACEO 的 coSNARKs 在 ZeroKnowledge 播客上

• 原文链接： medium.com/taipei-ethere...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～