如何在比特币上验证零知识证明（ZK证明）？

前言：本研究文章首次发布于我们投资组合公司 Polyhedra 的 科技博客，该公司正致力于比特币的可扩展性和互操作性。L2 Iterative 为 Polyhedra 撰写了这篇文章。

Polyhedra 一直在扩大其业务，专注于整个区块链领域中的新兴领域和零知识证明的应用。之前，我们专注于以太坊，并对零知识证明如何为以太坊生态系统贡献进行了 研究，并构建了 zkBridge（ https://zkbridge.com/），它为 LayerZero 跨链消息协议提供了零知识证明的安全保障。

今天，我们将注意力转向比特币。特别是，我们研究如何在比特币上验证 ZK 证明。我们不是第一个探索这个问题的团队。因此，我们以人类如何尝试将零知识证明引入比特币的简短历史开篇。

简短历史

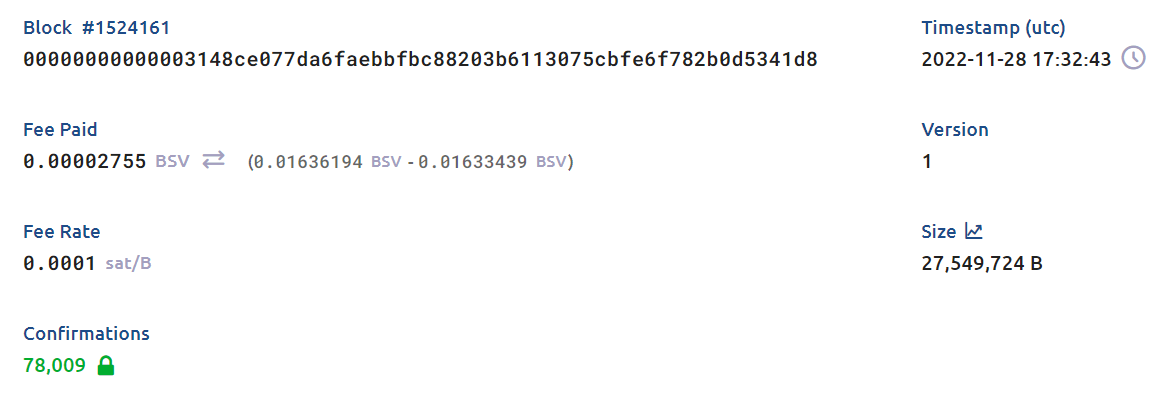
近年来最雄心勃勃的尝试是在比特币 SV 上 验证 BLS12-381 证明，这是由 sCrypt 团队发起的，但该尝试不适用于比特币——比特币 SV (BSV) 是比特币的一个硬分叉，现在是一个完全独立的链，具有许多差异。特别是，BSV 支持比特币不支持的 新操作码，并且具有更高的脚本大小限制。sCrypt 用于验证 BLS12-381 证明的交易可在 这里 找到，奢华地使用了这些新操作码，如 OP_NUM2BIN、OP_SPLIT、OP_CAT。该交易相当大——26MB——这在比特币中是不可能的，因为最大块大小为 4MB，而比特币的块间隔约为 10 分钟——我们需要为其他交易留下空间完成交易。

在这个雄心勃勃的尝试之前，比特币开发者实际上是第一批研究零知识证明的人，甚至在以太坊出现之前。早在 2011 年，前比特币核心开发者和 Blockstream 前首席技术官 Gregory Maxwell 提出了 “零知识条件支付”（Zero Knowledge Contingent Payment）。几年后，当零知识证明变得足够实用时，ZKCP 首次在比特币网络上实现（参见 这一公告）。然而，这并没有在比特币网络上验证 ZK 证明，而是离线进行了验证。这对 ZKCP 应用程序来说已经足够好，但对于一些其他需要链上 ZK 证明验证的应用来说并不适用。

最近关于在比特币上验证 ZK 证明的讨论发生在 Bitcoin StackExchange，QED Protocol 的 Carter Feldman 发现缺乏 OP_MUL 使得验证现代 ZK 证明变得困难。活跃的比特币核心开发者、Blockstream 的前联合创始人和核心工程师 Pieter Wuille 做出了如下回答。

“在我看来，即便存在 OP_MUL，在比特币脚本中实现 SNARK 验证器完全不可行。没有循环、椭圆曲线运算，甚至没有模指数运算，你必须被迫将计算完全展开为单个乘法。我无法想象在不使交易超出大小限制的情况下，能够真实地做到这一点。即便在某种情况下有可能做到，这也将是如此荒谬无效，我无法想象你会愿意将其用于除实验之外的任何事情。”

他继续补充：

“如果你的目标是在比特币脚本中进行实际的 SNARK 验证，也许你应该考虑一个提案，实际上添加 SNARK 验证操作码？”

这是我们讨论的一个良好起点。要知道为什么在比特币网络上验证 ZK 证明会困难，我们需要重新审视比特币脚本是什么——与 Solidity、与 EVM 有很大的不同。

比特币的操作码集合有限

与以太坊的智能合约及其围绕的 Solidity、OpenZeppelin 和 Reth 生态系统不同，比特币的一切要简单得多。比特币有自己的脚本语言和一个简单的堆栈机器。我们不称其为“虚拟机”（VM），因为它缺乏循环和条件跳转等简单控制流原语，它只是逐个执行操作码。

在比特币中验证 ZK 证明的主要挑战在于，比特币脚本仅支持 一小部分操作码，这使得它只能进行非常有限的计算。这并不总是这样。在 2010 年 8 月之前，比特币支持更多的操作码，包括 OP_CAT 和 OP_SUBSTR，而比特币 SV 后来重新引入了这些操作码。然而，由于对这些操作码中可能存在的漏洞的担忧，Satoshi 禁用了这些操作码。

这些操作码尚未被重新启用。因此，开发者一直在尝试使用现有的操作码“模拟”消失的操作码，但几乎没有成功。我们现在用 OP_MUL 和 OP_CAT 举例来展示这种不便。

以前，可以使用 OP_MUL 在堆栈中乘以两个数字（最多 4 字节）并将结果存回堆栈。OP_MUL 被移除后，数字的乘法必须通过 OP_ADD 和 OP_GREATERTHANOREQUAL 来模拟，使用 双加法 算法，这会需要数百条指令。

另一个被禁用且在 Twitter 上成为热点话题的操作码是 OP_CAT。你可能会看到一些比特币爱好者在他们的 Twitter 资料中包含 OP_CAT，以展示对恢复 OP_CAT 的支持。来自 Blockchain Beach 文章 的下图总结了它的历史。

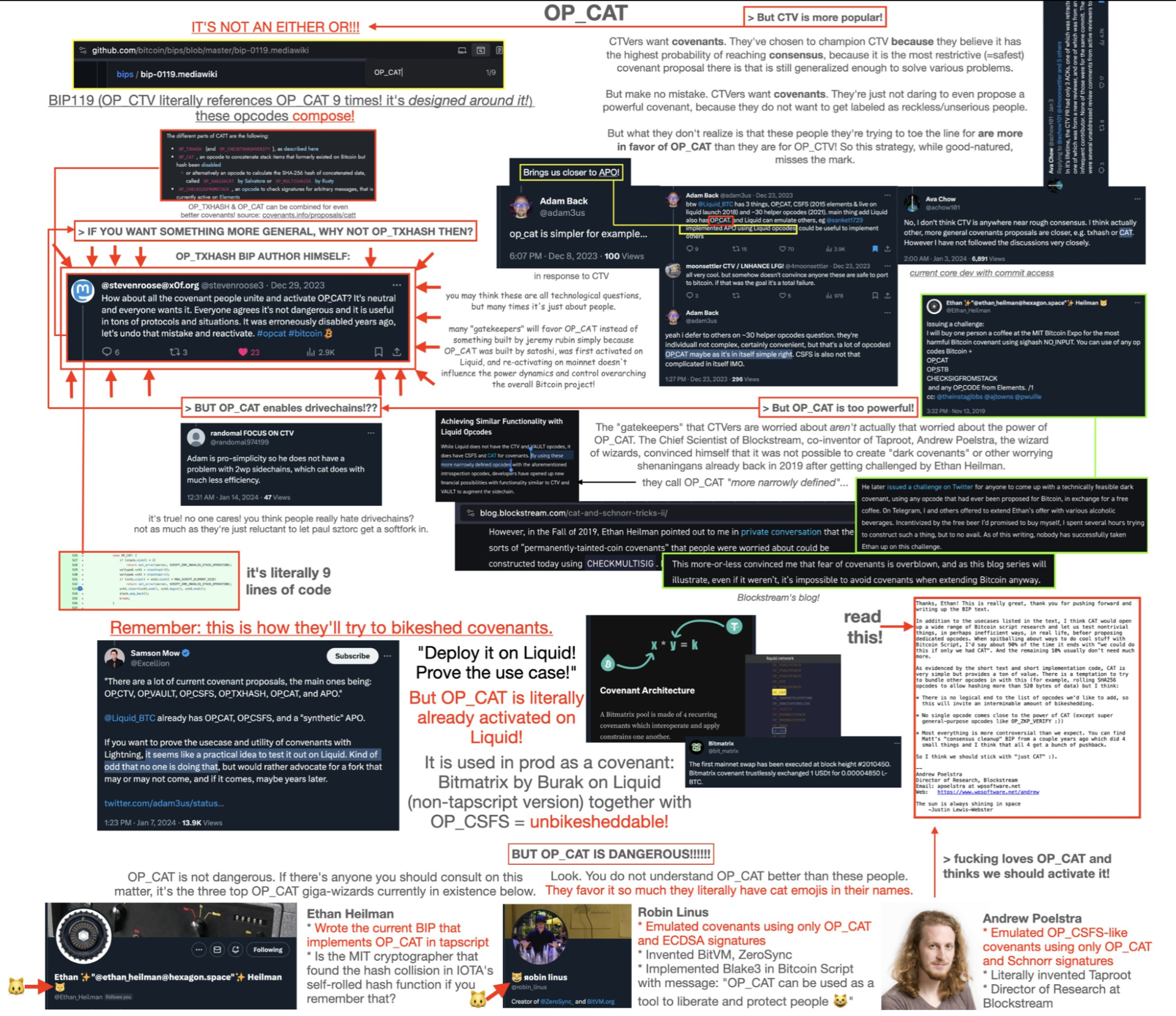
那么，什么是 OP_CAT？网络迷因似乎把一个猫放在每个地方（OP_CAT），但 CAT 意味着“连接”。它从堆栈获取两个字符串，并将它们组合成一个字符串。这是一个非常简单的功能，OP_CAT 仍然被禁用，导致了许多不便。

首先，我们尚未找到解决或模拟 OP_CAT 的方法。Robin Linus 收集了一系列关于比特币脚本的 新奇脚本，其中讨论了所有比特币脚本技巧，但它没有任何神奇的解决方案来模拟 OP_CAT，即使在特殊情况下。现有的操作码在这里无能为力。OP_ADD 仅适用于短输入，甚至无法处理稍微长一些的字符串。因此，在 Robin 的 Merkle 树路径验证 的脚本中，他不得不提出并承认：“该实现只需 OP_CAT。”在 2021 年，Blockstream 的 Andrew Poelstra 分享了他关于实现“契约”的 想法，但要求 OP_CAT，这可以在 Blockstream 的 Liquid Network 找到。他同样没有找到避免在比特币网络上对 OP_CAT 的需求的便利方法。

其次，OP_CAT恰巧对一些关键和基本的加密原语是不可或缺的，包括高效的 Merkle 树。为了使 Merkle 树高效，我们应该利用比特币脚本中的哈希操作码，如 OP_SHA256。现在的问题出现在 Merkle 树的压缩步骤中，该步骤通过对子节点哈希的拼接进行哈希来计算父节点的哈希，如果没有 OP_CAT，这似乎完全不可行——所有算术操作码都无法帮助，因为它们无法处理诸如 SHA256 哈希的较长输入，而其余操作码可以很容易地确认无能为力。不过，通过 OP_CAT，这就变得 微不足道。

恰好的是，大多数基于哈希函数的现代零知识证明都依赖于 Merkle 树。没有 OP_CAT，这将非常痛苦。

OP_CAT 的需求及其进展

与许多其他比特币开发者一样，我们团队一直在努力寻找创造性的方法来使用现有操作码验证 ZK 证明，但未能找到好的解决方案。这使我们感到重新启用 OP_CAT 可能是至关重要的。

对 OP_CAT 重新启用的许多积极意见，包括来自 Blockstream，许多比特币的分叉已然启用了它。人们对 OP_CAT 越来越宽容，原因有四：

• OP_CAT 的 C/C++ 代码相当简单，基本上只是调用 C++ 标准库的向量实现，如下图所示，以及 这里 的比特币代码库。

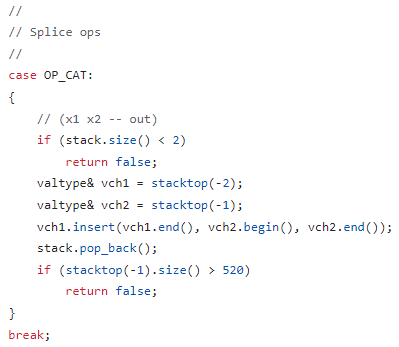
• OP_CAT 与 OP_LSHIFT 崩溃之间并没有直接关系，导致这些操作码在 2010 年被禁用。

• 可以通过限制 OP_CAT 输出长度有效防止攻击者使用 OP_CAT 创建非常长的字符串（通过每次翻倍其长度）。如上图所示，2010 年的 C++ 代码已经强制实施了 520 字节的长度限制。

• 重新启用 OP_CAT 仅需实现一次软分叉。

传统上，人们会倾向于不相信比特币会重新启用 OP_CAT，因为在过去十年中，没有禁用的操作码被复活过。但是，实际上，重新启用 OP_CAT 的进展似乎非常积极。bitcoin-dev 邮件列表中发生了大量比特币核心开发讨论。Ethan Heilman 在 2023 年 10 月启动了一项提案。

对此提案的回复是积极的。比特币关键开发者 Andrew Poelstra 如此表示。

“…在讨论如何以比特币脚本做一些有趣的事情时，大约 90% 的时间都以“如果我们有 CAT 就好了”告终。而剩下的 10% 通常所需也不多。”

“没有任何单个操作码能接近 CAT 的强大（除了像 OP_ZKP_VERIFY 这样的超通用操作码：）”

在 2023 年 12 月，已创建了草案 BIP（ https://github.com/bitcoin/bips/pull/1525）。尽管尚未分配 BIP 编号，但几位比特币开发人员已经对此进行了审查，并对所请求的编辑进行了几次迭代。

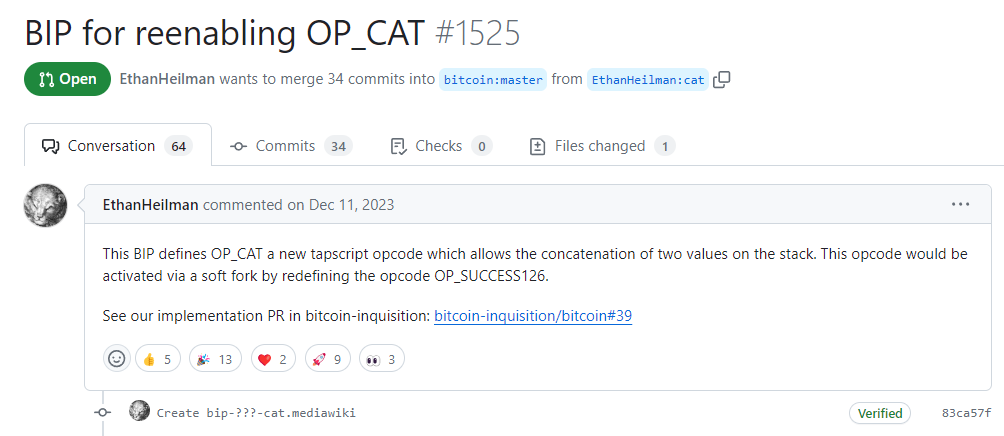
将其实施到比特币核心——比特币客户端实装的引用——的努力已启动。讨论目前在 Bitcoin Core PR Review Club 中进行。重新启用 OP_CAT 的拉取请求（ https://github.com/bitcoin-inquisition/bitcoin/pull/39）在过去几周内被积极更新和讨论。2024 年 3 月 6 日，比特币核心 PR 评审俱乐部举行会议讨论 OP_CAT。

如果拉取请求合并，讨论将转移到比特币核心主存储库（ https://github.com/bitcoin/bitcoin/pull/29247），如下所示。OP_CAT 如果通过所有必要的流程，就会将该 PR 合并，并在新的比特币核心客户端版本中发布，软分叉将开启此功能。

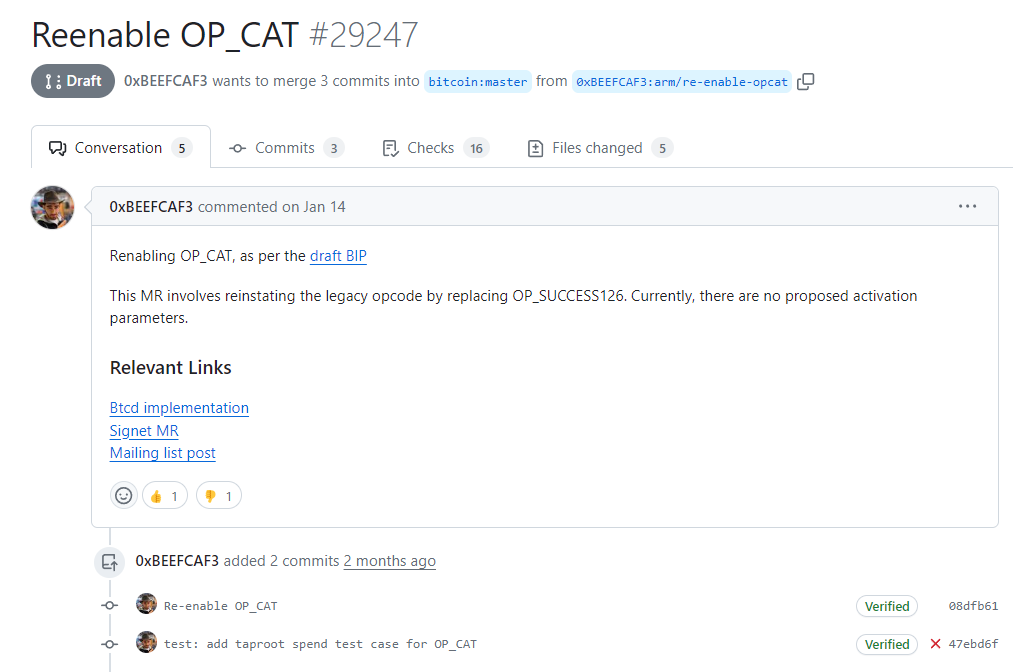
很难预测整个过程会花费多长时间。这是禁用的操作码于 2010 年首次被重新启用，也是第二次将主要操作码添加到比特币（上一次是 OP_CHECKSIGADD 以支持 Tapscript）。

然而，我们相信比特币社区将很快恢复 OP_CAT。

首先，此刻比特币的路线图中没有其他重大变化，OP_CAT 已成为当前关注的焦点。

其次，OP_CAT 已被讨论多年，并在比特币网络的变种中实现，并且已被充分研究。这可以从比特币核心开发者之间的对话中看出，大家似乎形成了共识。

总之，我们对 OP_CAT 将被带回比特币网络抱有乐观态度，我们相信这将是比特币生态系统的重要时刻。

在文章的其余部分，我们将分享我们如何在比特币网络中验证零知识证明的思路，假设 OP_CAT 已启用。

定义比特币友好的证明系统

sCrypt 对比特币 SV 的上一尝试，在比特币网络上验证 BLS12-381 Groth16 证明，仍然不适用于比特币网络——sCrypt 的实现已经假定 OP_CAT 的存在。sCrypt 实现不起作用的主要原因是脚本太长，相应的交易如下面所示，无法容纳在一个比特币块中。脚本大小必须小于 4MB，否则矿工无法将其包含在任何区块中。

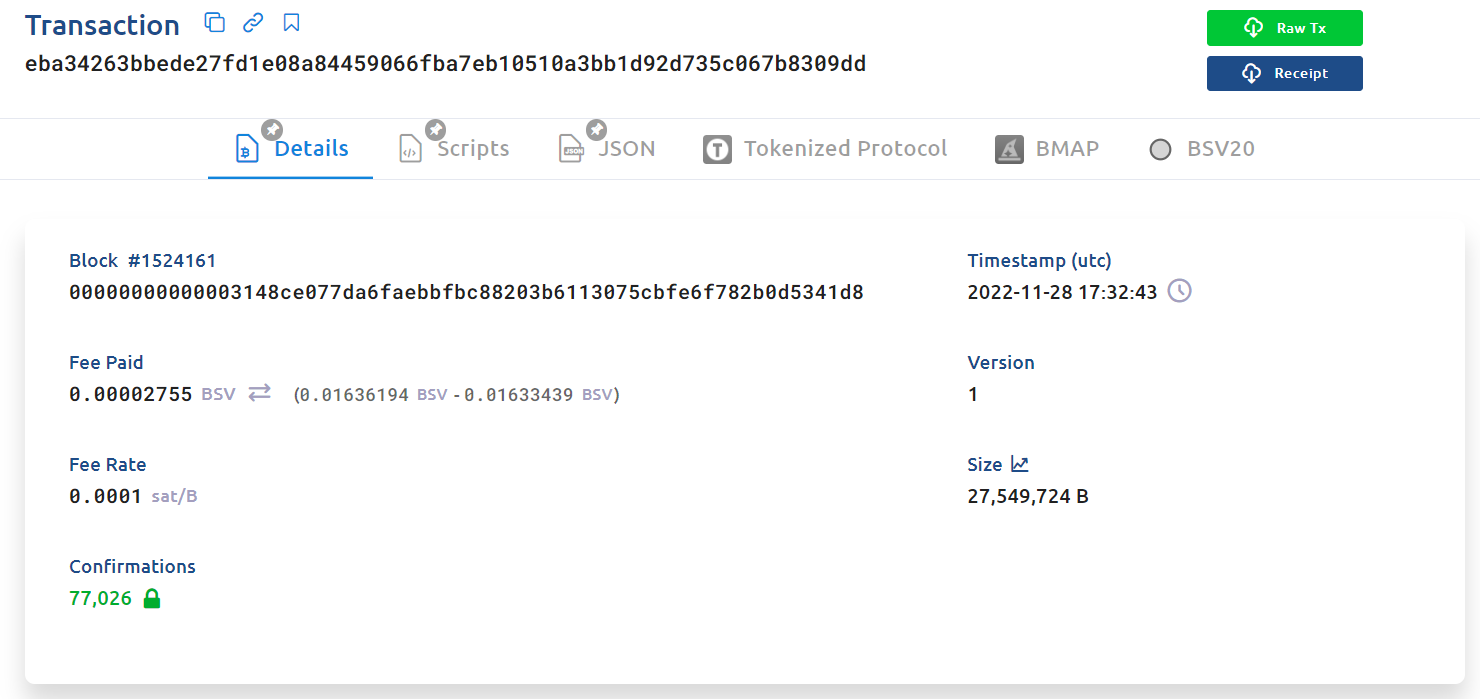
这使我们能够精准地定义一个零知识证明系统“比特币友好”的含义。自 2017 年 SegWit 升级以来，比特币网络通过 “权重单位”（weight units） 来测量一个块的大小，且块的限制为 400 万权重单位。我们从比特币区块探测器的观察表明，许多区块已消耗其装机的 400 万权重单位配额，每个区块的大小在 1MB 到 2MB 之间。

在我们将使用的 pay-to-taproot (P2TR) 交易中，交易所消耗的权重单位数量是通过一组 规则 计算的，因此交易中的某些字节费用为 4 权重单位，而另一些字节仅费用为 1 权重单位。将某些字节赋予较低权重单位费用（即“折扣”）的原理在于，这些字节用于确定交易是否有效，交易一旦被验证，这些字节就不需要由所有完整节点永久存储，因此它们对比特币网络的存储开销贡献较少。令我们欣慰的是，比特币脚本，其将是 P2TR 交易中的见证脚本，享有这一折扣。

P2TR 为比特币脚本带来的另一重要意义是它提升了比特币脚本的多数大小限制。只要它能适应一个区块，任何矿工都不妨将其包含在内。然而，这并不意味着普通用户可以进行 400 万字节的比特币脚本。根据 默认政策，许多节点只会中继那些消耗不到 400k 权重单位（区块限制的 1/10）的交易，如果有人真诚地希望提交更大的交易，则需要与矿工合作，正如比特币 StackExchange 上的一些帖子所指出的（ [1]， [2]）。

P2TR 在比特币中实现 ZK 证明验证的可能性中起到了重要作用。来自 @therationalroot 的下图总结了其优点。

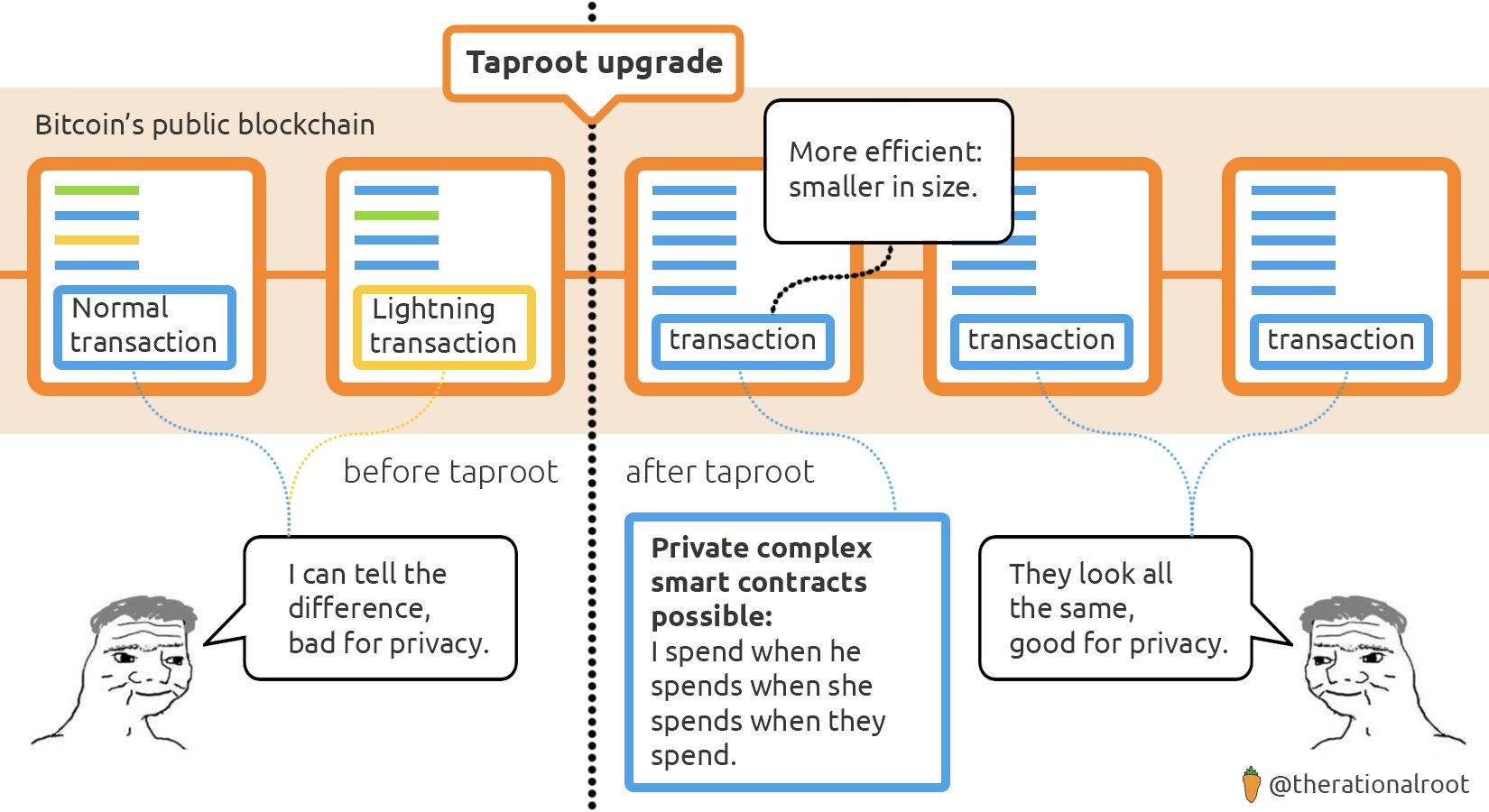
我们还应注意的另一限制是堆栈大小。比特币脚本目前将堆栈大小限制为 1000。一个程序不能创建超过 1000 个堆栈元素。这大致意味着一个比特币脚本理论上可访问的“工作内存”为 0.5MB。我们应该确保程序在内存限制内正常运行。然而，无需进一步优化，因为交易费用不依赖于峰值堆栈大小。

现在，我们拥有定义比特币友好的所有信息。基本上，我们想要一个证明系统，其验证算法可以在比特币脚本中用尽可能少的权重单位表示，并且可以在堆栈限制和其他规则内可执行。这转化为对证明系统一个期望，表示其验证算法所需的字节数尽可能少。

衡量比特币友好的另一个次要指标是，如果我们拥有两个具有相似权重单位的证明系统，验证算法是否能够方便地拆分为几笔交易，以便每笔交易完成几步的证明验证。如果独立的比特币脚本在单次提取得证明验证中仍超出限制，在这种情况下，我们可能需要某种 契约 来强制这些交易之间的关系，这会从 OP_CAT 中受惠，但这需要更多的研究。

在比特币脚本中简洁表达计算的诀窍——即，不使用过多的权重单位——是尽可能利用操作码。例如，比特币脚本本身通过五个操作码（十六进制表示分别为 0xa6-0xaa）原生支持哈希函数：

• OP_RIPEMD160
• OP_SHA1
• OP_SHA256
• OP_HASH160
• OP_HASH256

哈希操作无论长度如何，仅花费一个权重单位。如果必须使用其余操作码模拟哈希操作，如果假设 OP_CAT 可用，仍可能需要至少 60k 权重单位（以布尔电路的形式运行 SHA256），还有其他成本，如访问堆栈。目前的堆栈可能不足以运行这个程序。我们可以看到尽可能使用现有操作码的重要性。

我们特别关注“哈希”，因为许多现代零知识证明协议恰好依赖于哈希函数。

寻找比特币友好的证明系统

现代零知识证明的生产级可以大致分为两大类：

• 基于椭圆曲线的配对证明（如 BN254）
  • 示例包括 Groth16、Plonk 和 Marlin
• 基于哈希函数的证明
  • 示例包括 STARK 及其多种变体和实现

我们首先的想法是，基于配对的证明系统不太可能在比特币上工作，原因有几点。

• 在更大且结构不太规整的质数上的计算。 基于配对的证明系统依靠椭圆曲线。要确保椭圆曲线安全，其质数域模数必须至少约为 256 位。通常，我们通过显式公式构建配对友好的曲线，如 BN 曲线的情况。这种构造方法的缺点是我们无法选择小质数，并且可能需要实现诸如 Montgomery reduction 的东西来处理这些结构不规则的大质数，从而增加复杂度。
• 模拟的困难性。 为了验证基于配对的证明，验证者需要对曲线上的几个点执行标量乘法及所谓的“配对”步骤。这可能非常繁重。在这里回想一下， sCrypt 的例子远远超出了标准块限制，尽管它利用了如在比特币 SV 上可用的新操作码如 OP_MUL。

因此，我们的重点转向基于哈希的证明系统。Robin Linus 最近在 Twitter 上发了一个 推文，询问是否有人采取过这样的措施。

核心思想是，在有了 OP_CAT 之后，与 Merkle 树相关联的计算部分，可以像我们提到的那样，使用现有的哈希操作码，它们仅消耗非常小的权重单位。其余计算相对于基于配对的证明系统而言要简单得多，因为它可以涉及小质数。这种灵活性是性能的关键。

我们发现某些已经在 STARK 中使用的质数是比特币友好的。要使质数成为比特币友好，它需要满足一个要求：质数小于 2^31。这确保了两数相加不会超过 2^32。

一组质数满足这一要求。

• M31 (2^31 - 1)，已用于 Circle STARK。
• BabyBear (15 * 2^27 + 1)，已在 RISC Zero 中使用。

对比特币而言，M31 和 BabyBear 彼此间并无太大差异，因为它们的算术运算将几乎以相同的方式被模拟。

其好处在于，这使我们能够使用 OP_ADD 和 OP_SUB 进行所有加法和减法。我们可以通过“0 OP_LESSTHAN”来检测溢出，并可以通过 OP_ADD 和其他操作码迅速纠正溢出。

为了乘以两个数字，由于 OP_MUL 仍然被禁用，我们需要通过双加法实现。BitVM 已经 实现 了这一技术。

读者可能想知道另一个质数 Goldilocks64 (2^64 - 2^32 + 1) 是否比特币友好。由于这个质数是 64 位的，我们无法轻松利用现有比特币操作码对其进行仿真，因此我们认为可以排除 Goldilocks64。

现在，一个悬而未决的问题是，既然 STARK 有如此多的变体，我们应该选择哪一个？这实际上是在询问我们应该选择什么样的算术化在证明系统中。

一个候选的解决方案是 R1CS，它已在 Groth16 中使用。《Fractal》（https://eprint.iacr.org/2019/1076.pdf）论文（EUROCRYPT 19）展示了如何在基于哈希的证明系统中实现 R1CS，并使其验证者尽可能高效。

另一个候选解决方案是教科书式的 Plonk，在其中每个门有三根线，两个用于输入，一根用于输出，每个门仅执行一次简单的两个输入的线性组合。我们认为，这可能在最终验证成本方面比 R1CS 更简单。

仍然需要进行一些工作来实验我们以上提供的提案，但基于我们对 ZKP 领域的理解，我们的讨论应该足够全面。

一个可能对从业者有帮助的附加备注是，为了在基于哈希的证明系统中获得足够的安全级别，有几个参数可供调整。Starkware 使用一种被称为 grinding 的技术，增加工作量证明组件以增强安全性，借此可以减少查询或使用更通过验证的编码率，同时仍保持相同的安全级别。由于在比特币中验证 grinding 对验证者而言很简单，因此我们特别喜欢这个想法。最近的研究，名为 STIR，与此非常相关，因为它提供了一种进一步降低验证成本的技术。

最后但同样重要的是，STARK 相比于基于配对的证明系统的一个好处是，STARK 被认为具备后量子安全性，而基于配对的证明系统则被认为不具备后量子性。换句话说，STARK 可能是一个更合适的长期选择。

我们还有很多工作要做，以了解验证者的具体成本，我们相信实际上需要通过实现来学习。但是，我认为整体路线图是明确的，仅需时间问题。请注意，我们仍然担心，最终即使更适合比特币的证明系统也无法适应交易，在这种情况下我们需要进行更多优化。本文将讨论其中的一些。

现在，人们可能会想，专注于“验证者”的比特币友好性，是否会对“证明者”造成沉重的代价。这是我们之前提到的教科书式 Plonk 证明系统的一个潜在问题——由于其简化的结构，相同的计算可能在呈现程序的方式上产生更多冗余，并且执行速度较慢（考虑一台具有更简单指令集的 CPU，可能需要使用更多指令以达到相同的功能）。教科书证明者与高度优化证明者（如 Scroll、Polygon Miden、RISC Zero 中使用的 Halo2）之间的证明效率差距可能会很显著。

这可以通过一种设计哲学“ SHARP”，在 2019 年由 Mariana Raykova、Eran Tromer 和 Madars Virza 提出的来解决。其理念是可以通过使用两个（或更多）证明系统来平衡证明者效率和验证者效率之间的最佳折衷：

• 一些证明系统，证明者效率较好，但验证者效率可能不理想（通常是由于算术化复杂但因此更具表现力）。
• 一个最终证明系统，证明者效率可能中等，但验证者效率好。

将这些不同的证明系统结合在一起的方式是通过 递归验证。要证明某事是真的，证明系统可以验证其计算，或者，执行对一个现有证明进行验证，以确认该计算为真。对于足够大的计算，后者通常更有效，因为一般而言，验证一个证明的复杂性比验证相应的计算要小。

这一技术已在生产中得到应用。下图展示了 Polygon zkEVM 如何使用不同的证明系统生成一个验证大量计算单一证明的证明。这张图中展示的多个递归证明者并不相同。例如，最后阶段使用的递归证明者切换到不同的有限域，以使最后的 SNARK 阶段的证明验证者高效。

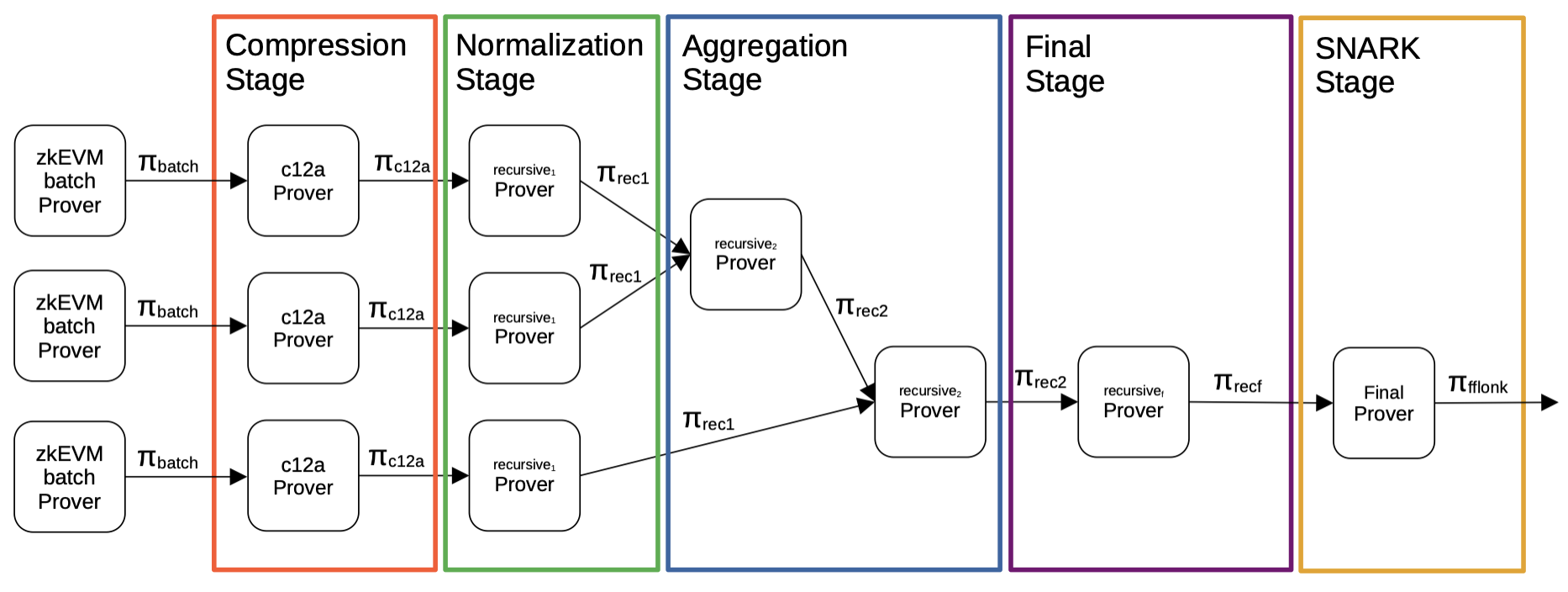
因此，我们将做的是用证明者高效的证明系统来运行实际的证明验证，同时也使用证明者高效的证明系统将这些证明汇总成一个单一的证明，最后我们将使用验证者高效（更具体地说，比特币友好的）证明系统将其转换成比特币友好的证明。

这使我们能够避免因比特币友好性而对证明者效率造成的惩罚。

使用 OP_CHECKSIG 进行交易自省

如果解决方案成功，使用 ZK 证明可能能够实施非常复杂的契约，因为它实现了通用的交易自省。

比特币中的 契约（Covenants） 是指脚本公钥强制执行某些规则，使得需要在该脚本公钥底下支出 UTXO 的交易。这在很大程度上依赖于 OP_CAT。其理念是，脚本公钥可以使用 OP_CHECKSIG 来验证当前交易的签名，签名中包含诸如输出列表等信息，脚本公钥可以决定是否使该交易失效，若脚本不希望允许这样的输出。

一个简单的例子，展示了 OP_CAT 和 OP_CHECKSIG 功能强大的由 Rijndael（@rot13maxi）发出的 推文。

@rot13maxi 基本创建了一个需要支出交易遵循特定格式的 UTXO。这个例子很棒，因为它只依赖现有操作码和 OP_CAT，并且脚本足够简短。限制是，它可能无法支持更多复杂的规则或具有更多灵活性的交易。

sCrypt 在比特币 SV 上尝试使用契约在交易之间传递状态，从而使得脚本变得有状态。这里的理念相似，运用 OP_CAT 和 OP_CHECKSIG，以及 Andrew Poelstra 讨论的 Schnorr 技巧。

如果我们能够在比特币中实际验证 ZK 证明，并且这种验证变得足够高效，我们可以实现通用交易自省，如下所示。

• 计算交易的哈希。
• 使用 OP_CHECKSIG 根据 Schnorr 技巧验证该哈希。
• 在哈希的基础上生成零知识证明，断言：
  • 让 b 为此签名下的交易主体。
  • 验证签名是否为消息 b 的有效签名。
  • 检查 b 是否满足特定规则。

ZK 带来的好处在于“满足特定规则”这几个字。因为今天的零知识证明极为通用，基本上可以施行任何常规计算机能够完成的规则。例如， RISC Zero 为一通用虚拟机，可以运行 RISC-V 指令。只需将一个程序编译成 RISC-V，即可计算其执行的证明。现如今，人们可以轻松将 Rust 和 C++ 代码跨编译到 RISC-V（请参见如何通过 ZK 验证游戏 Doom）。下表展示了 RISC Zero 的证明生成性能。一台 M2 MacBook 可以以 100kHz 的速度证明 RISC-V CPU 执行。借助集群计算，可以线性扩展。这使我们能够处理很多比特币生态系统以前未想到的复杂程序。

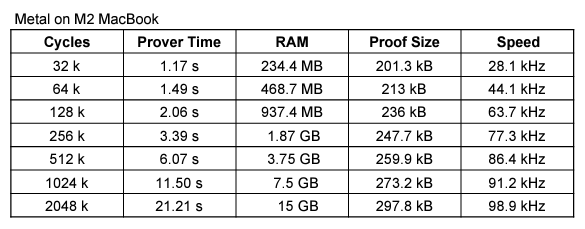
通用零知识可以做得更多。例如，通过交易自省，ZK 证明可以知道输入的 txid，并且因为 txid 是前一个交易信息的哈希，这允许 ZK 读取前一个交易。

• 让 prev[0] 为创建第 1 个输入的前一个交易。
• 验证 prev[0] 是否对应于新交易主体中出现的 txid h[0]。
• 将 prev[0] 中的数据作为对前一个交易的可靠参考。

由于每笔交易可以有多个输入来自不同的交易，因此可以存在 prev[1]、prev[2]、prev[3] 等等，代表其他输入的交易。

这还并未结束。现在我们能够访问前一个交易，也可以访问前一个交易的前一个交易。这能够追溯到创世交易。这使我们能够探索比特币历史数据的一部分，这些数据为当前交易的祖先。

这一设计可以启用多个应用场景。如果我们仔细想想，游戏规则的推动者是零知识证明，它提供了几个有用的功能。

• 通用计算。 如果验证零知识证明变得可行，交易自省将不再受到比特币脚本的限制。如今在生产中使用的现代零知识证明，能够实际验证从高级语言例如 Rust 和 C++ 编译的程序，并且这些程序拥有程序计数器，能够拥有动态控制流，且具备大量可访问的随机访问内存。这从根源上消除了将比特币脚本推向图灵完备或通用的必要性，因为这样的计算可以委派给 ZK，从而进一步减少网络开销。

• 增量计算。 今天的零知识证明可以以非常可组合的方式生成，因为我们可以实际在另一个零知识证明内验证一个零知识证明。这意味着，在考虑状态机的时候，从 A 状态证明到 Z 状态，能够通过验证一个已经验证从 A 过渡到 Y 状态的证明并从 Y 状态持续进行到 Z 状态。在这里，验证从 A 到 Y 的证明会比从 A 到 Y 重新进行计算快得多。比特币区块链的轻客户端可以视为一个状态机，这意味着可以生成比特币历史的 ZK 证明，并通过增量更新进行新的区块刷新。

• 简洁验证。 通过递归组成，零知识证明的一个关键属性是我们可以使验证者的开销保持常数，无论在证明中所验证的实际计算量。因此，即便一个证明可能探查多年的比特币历史，其证明验证成本仍然可以与另一个完成非常简单操作的证明几乎相同。这也是零知识证明在以太坊生态系统中被广泛用于构建 ZK-Rollups 的原因。

交易自省的能力还可以超越比特币网络，通过使用 ZK 桥。ZK 桥的理念是可以有效运行另一条链的轻客户端，查询状态并以 ZK 验证所有执行过程。许多 L1 区块链基于 PoW 或 PoS，因此 ZK 桥能够验证 PoW 和 PoS，以检测并拒绝错误的分叉，正确链被选择后，它可以使用 ZK 以可验证的方式读取区块链，就像比特币的 简化支付验证（SPV）一样。

尽管如此，正如前面提到的，这仅在零知识证明足够高效，以至于我们能够将其适应所有比特币脚本限制（堆栈大小、权重单位）的情况下才能实现。而这又取决于比特币网络上 ZK 证明验证的成本是否合理。我们无法得出一个明确的答案来判断其是否可行。Robin Linus 建议 400 万重量单位足以进行大量计算。但是，我们认为我们需要首先投入实际的工程努力。如果成本过高，我们可能需要进行更多优化，接下来我们将讨论一些我们的想法。

将证明验证拆分为多个交易

假设 ZK 证明验证不能在单个交易中完成，我们需要找到创造性的方式将一批交易链接在一起，让它们各自执行部分 ZK 证明验证。

sCrypt 上的几篇文章（1，2，3），虽然依赖于 Bitcoin SV，但提供了如何实现这一点的一般思路。通过使用 OP_CHECKSIG 和——自然，OP_CAT——一个输入的公钥是一个脚本，可以对当该输入被花费时，强制其他输入和输出的行为。

想法如下。假设我们自己是一个证明者。证明者的目标是让验证者相信所做的计算。

首先，证明者可以将计算拆分为 N 个脚本。每个脚本执行部分验证。然后，证明者创建其第一个交易，如下所示。

[input] => out[1], out[2], …, out[N], out[N+1]

这里，out[1] 到 out[N] 将是进行计算的 pay-to-taproot (P2TR)。out[N+1] 是一个输出，用于记录当前证明者的公钥。因此，它可以是一个简单的脚本，如下所示：

OP_RETURN {prover public key}

这个交易不会很昂贵，因为在这个交易中，无论 out[1] 到 out[N] 中的脚本多么复杂，这个交易包含的只有脚本的哈希。因此，这个交易的大小较小。

现在，对于每个 out[1] 到 out[N]，它们将按要求执行计算，并使用 OP_CHECKSIG 和 OP_CAT 强制执行以下条件。

• 该交易只有一个输入和一个输出。
• 输入的 txid 通过给定第一个交易重新计算：[input] => out[1]，out[2]，…，out[N]，out[N+1]。
• 需要验证者关于此交易的证明者公钥的签名，如 out[N+1] 中所给。这是为了防止 Bitcoin 网络上的其他人花费 out[1] 到 out[N]。
• 输出将是一个非常简单的，只有在提供有效签名的情况下，才能在证明者的公钥下花费——这将使用 OP_CHECKSIG 避免可塑性——而且脚本包含两个额外的数据元素：一个表示共享数据的哈希，应该在所有 out[1]、out[2]、……、out[N] 中相同，另一个未使用的随机堆栈元素，以促进 Andrew Poelstra 讨论的 Schnorr trick，因为我们需要确保 OP_CHECKSIG 验证的前像的哈希以 0x01 结尾。

因此，我们将创建 N 个交易，每个交易解决一个 out[i] 并产生一个输出，我们称其为 cert[i]。注意 cert[i] 包含共享数据的哈希，这个哈希应该在所有这些交易中是相同的，即使它们可能位于不同的块中。这些 N 个交易看起来如下。

out[1] => cert[1]
out[2] => cert[2]
…
out[N] => cert[N]

现在，假设证明者需要说服一个验证者（这是一种 pay-to-taproot UTXO，而证明者无法控制它），证明者向验证者展示所有 cert[i]，通过创建以下交易。

verifier-in, cert[1], cert[2], …, cert[N] => verifier-out

需要做一些小的调整以启用 Schnorr trick 来帮助自省。整体交易流程如下所示。

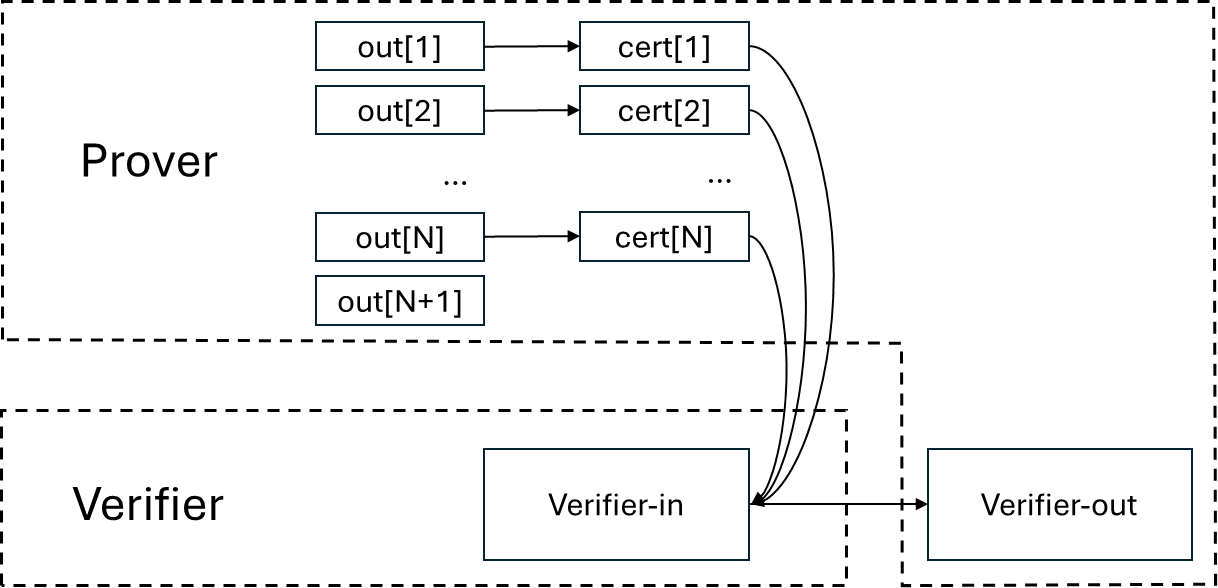
verifier-in 将执行以下操作：

• 通过 OP_CHECKSIG 和 OP_CAT 优化 cert[1] 到 cert[N] 的 txid，获取两个输出。
• 检查 verifier-out 是否如预期。
• 使用 cert[1]、cert[2]、…、cert[N] 的 txid，恢复交易 out[1] => cert[1]、out[2] => cert[2]、…、out[N] => cert[N]，从而获得 out[1]、out[2]、…、out[N] 的 txid。
• 检查 out[1]、out[2]、…、out[N] 是否有相同的 txid。
• 使用 out[1] 到 out[N] 的 txid，恢复交易 [input] => out[1]，out[2]，…，out[N]，out[N+1]。
• 检查对应于被接受的 ZK 证明验证过程的正确 pay-to-taproot 哈希是否在 out[1]、out[2]、…、out[N] 中使用。
• 检查 cert[1]、cert[2]、…、cert[N] 是否包含正确的共享数据。注意，共享数据是必要的，因为如果 verifier-in 不检查共享数据，则证明者可以提供任何证明，而被证明的事项可能与验证者正在寻找的内容无关。

重要的是我们使用 Taproot，因为 OP_CHECKSIG 在 Taproot 和非 Taproot 交易中表现非常不同——例如，它现在使用 Schnorr 签名，对于使交易自省能够实现的 Schnorr trick 至关重要，并且计算交易哈希的方式也不同，因为它不再包括脚本代码。

我们需要声明的是，我们实际上还没有实现上述想法，全面的实施是需要查看所有脚本是否可以在各自限制内完成（这当然需要 STARK 证明者的全面实现）。特别是，我们想要看看我们是否可以确保所有交易都是“标准”的（遵循 Bitcoin Core 的 policy.h 中设定的软限制），这样我们就不需要与矿工协调来提交交易。与矿工协同并非不可能。这样的服务是由 Marathon Digital 提供的 Slipstream：“Slipstream 是一个直接提交大型或非标准 Bitcoin 交易给 Marathon 的服务……如果你的交易满足 Marathon 的最低费用标准并符合 Bitcoin 的共识规则，Marathon 会将其加入他们的内存池以进行矿工处理。”

另一个考虑是我们希望降低证明解决的等待时间。如上面的设计确实试图促进这一点，允许所有证明生成交易同时提交到 P2P 网络。

读者可能会想一次提交所有交易是否可行，因为某些交易依赖于其他交易，并且如果前一个交易未被确认，这些交易将失败。读者可能会想矿工是否能够将这些交易放入同一个区块，或者 Bitcoin 网络中的交易必须只使用前一个区块中的前一个交易。

然而，这对于 Bitcoin 网络来说并不是什么重大问题，因为 Bitcoin 允许这种灵活性。事实上，Bitcoin 有一种名为 Child Pays for Parent (CPFP) 的技术，已经利用了可以将具有依赖关系的交易一起提交到内存池的事实。交易可以使用先前交易的输出，只要满足共识规则：

Bitcoin 共识规则要求创建一个输出的交易必须出现在其区块链上比花费该输出的交易早——包括如果这些交易都包含在相同的区块中，父交易必须早于子交易出现。

因此，可以同时提交所有这些交易，并等待 P2P 网络对其进行解决。请注意，这些交易的设计旨在使网络易于解决。

• 第一个交易 [input] => out[1]，out[2]，…，out[N]，out[N+1]，仅依赖于证明系统以及证明者的公钥，因此证明者确实可以提前制作此交易。如果不是，证明者也可以与其他交易一起提交此交易。
• 接下来的 N 个交易 out[i] => cert[i]，仅依赖于第一个交易，并且不会相互干扰。Bitcoin 网络中的矿工可以以任意顺序接受这些交易，但我们设想，以合理的费用，矿工被鼓励尽快包含这些交易。
• 最后一个交易 verifier-in，cert[1]，cert[2]，…，cert[N] => verifier-out，可以与其他交易一起提交到 P2P 网络，预计将在所有 N 个交易确认后执行。

然而，总有选择与矿工合作来让交易被接受，我们设想最终可能会有一个区块空间保留系统，以便更可预测的延迟和结果，这可能使我们免于进行更多的黑客操作。

关于分割验证的欺诈证明

另一个想法是借用乐观 Rollup 的思路，并将其打造为欺诈证明，类似于 BitVM 所做的，它可以从我们刚刚展示的分割验证实现开始。欺诈证明避免了实际执行计算的需要，并依赖于第三方——公众中的挑战者——在 Bitcoin 网络上使任何欺诈证明的声明无效。

一个重要的细微差别是，欺诈证明引入了另一个要求——数据发布。为了说服验证者某个声明是真实的，因为没有公众生成的欺诈证明，验证者需要确信用于让公众质疑声明所需的任何数据已经提供——具体来说，是发布在 Bitcoin 网络上的。

我们提出了这个高层的想法，我们承认需要详细的实现来验证这一想法是否能成功。证明者在第一步中创建一个交易，如下所示。

[input] => out[1], out[2], …, out[N], out[N+1], da[1], da[2], …, da[N]

其中出自 out[1] 到 out[N] 是可以通过两种方式花费的 pay-to-taproot：

• 对于 out[i]，提供在 da[i] 中描述的见证和 ZK 证明的公开输入，并展示这个见证不起作用，或者 da[i] 中的数据与 out[N+1] 中指定的哈希不一致。如果这是满足的，将使用 OP_CHECKSIG 和 OP_CAT，加上 Schnorr 的技巧，确保输出是对挑战者的简单支付。它使用相同的交易自省技术来读取父交易中的 out[N+1]。这将花费输出，因此防止再次花费相同的输出。
• 或者，要求在证明者公钥下的签名（可以编码在 out[i] 的此 tapleaf 中）。这个 tapleaf 是愉快路径，它对花费该输出的交易不会有额外要求。

特殊输出 out[N+1] 将编码信息，例如：

OP_RETURN {public input} {hash of da[1]} {hash of da[2]} … {hash of da[N]}

每个 da[1] 到 da[N] 都是只能通过提供在 out[N+1] 中给定的哈希的前像来花费的 pay-to-taproot。

• 此方法使用交易自省技术回到父交易并读取 out[N+1] 中的哈希。
• 它检查初始堆栈（在适当连接 OP_CAT 后）是否包含可以哈希成 out[N+1] 中概述的哈希的数据。注意，由于堆栈大小限制，计算这个哈希需要定制，以适应 OP_SHA256 只能哈希至多 520 字节的数据的事实，例如将数据拆分为多个块，单独哈希它们，然后以 Merkle 树风格迭代地哈希结果。
• 它产生一个非常简单的输出，仅在提供在证明者公钥下的有效签名时才能花费——这将使用 OP_CHECKSIG来避免可塑性。我们称这个输出为 timelock[i]。这个输出将有时间锁，例如只能在交易被确认很长时间后才能被花费。时间锁会允许某种随机性来促进 Schnorr 技术。
• 因此，花费 da[i] 将在 Bitcoin 区块链上公开必要的数据。

因此可以执行如下形式的交易：

da[i] => timelock[i]

现在，证明者被要求将以下交易提交到 Bitcoin 区块链：

[input] => out[1], out[2], …, out[N], out[N+1], da[1], da[2], …, da[N]
da[1] => timelock[1]
da[2] => timelock[2]
......
da[N] => timelock[N]

可以有一种替代设计，试图通过将 da[i] 的交易自省推迟到验证者，从而避免需要的操作，这可能有助于降低成本，因为 da[1]、……、da[N] 都具有相同的 txid。我们会将其留作未来研究。

这将现在允许一个挑战者提交欺诈证明，如果任何事情看起来不正确。例如，如果挑战者在从 Bitcoin 网络获得数据后，相信 out[i] 不会匹配，那么根据 out[i] 的定义，挑战者可以使用第一个 tapleaf 花费 out[i]，这样就会阻止证明者稍后使用第二个 tapleaf 花费 out[i]。例如，如果挑战者发现 out[j] 可被挑战，可以提交如下交易。

out[j] => $

这里 $ 代表挑战者可以作为奖励获得的存款。总结一下，挑战的工作原理如下。

如果足够的时间过去，但没有人能够挑战 out[1] 到 out[N] 中的任何输出，那么证明者现在可以向验证者提交证明。

verifier-in, out[1], …, out[N] timelock[1], timelock[2], …, timelock[N] => verifier-out

工作流的愉快路径将看起来像这样。

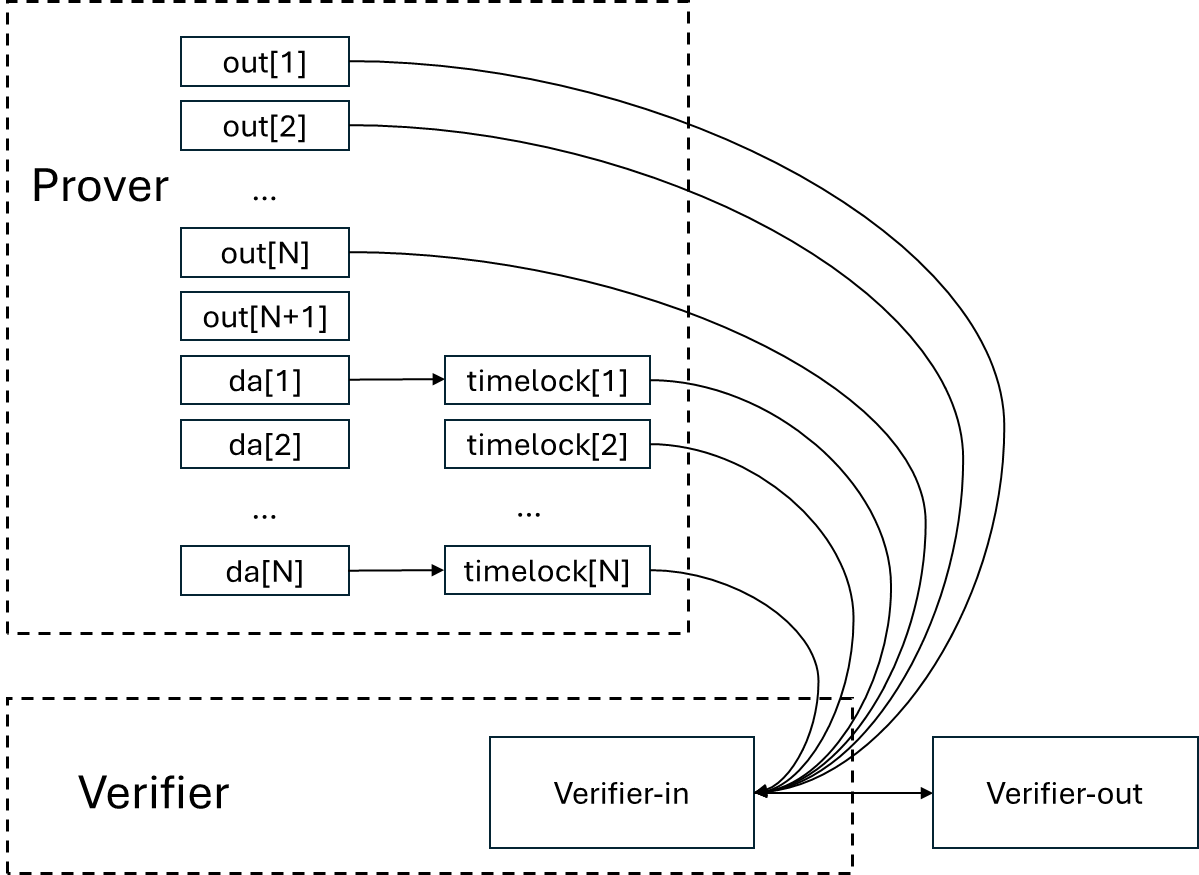
verifier-in 将执行类似的检查：

• 通过 OP_CHECKSIG 和 OP_CAT 获取 timelock[1] 到 timelock[N] 的 txid，并获取两个输出。
• 检查 verifier-out 是否如预期。
• 使用 timelock[1]、timelock[2]、…、timelock[N] 的 txid，恢复交易 da[1] => timelock[1]、da[2] => timelock[2]、…、da[N] => timelock[N]，从而获得 da[1]、da[2]、…、da[N] 的 txid。
• 使用 out[1] 到 out[N] 的 txid，恢复交易 [input] => out[1]，out[2]，…，out[N]，out[N+1]，da[1]，da[2]，…，da[N]。
• 检查 out[1]、out[2]、…、out[N]、da[1]、da[2]、…、da[N] 是否具有相同的 txid。
• 检查 out[1]、out[2]、…、out[N] 中是否使用了与被接受的 ZK 证明验证过程相对应的正确 pay-to-taproot 哈希，da[1]、da[2]、…、da[N] 中是否使用了被接受的数据发布过程。
• 检查 out[N+1] 中的公共输入数据是否与验证者相关。
• 检查 da[1]、…、da[N] 是否具有正确的相对时间锁，这意味着 out[1]、…、out[N] 是可用的，并且 da[1]、…、da[N] 已被发布。额外的规则可能会治理相对时间锁需要多长，具体取决于用例，并考虑到 Bitcoin 网络可能的拥堵。

使用 BitVM 的欺诈证明

另一个解决方案，可能更为通用，可以用更高级的语言进行编程，是使用 BitVM。

我们想强调的是，基于我们与 Robin Linus 的对话，目前仓库中的 BitVM 设计与许多人所熟悉的白皮书版本非常不同。鼓励读者从 GitHub 仓库中查看最新的 BitVM 设计。这个 图 概述了 BitVM 的新设计，应该不言自明。

如果你访问 BitVM 仓库，你会发现今天的 BitVM 类似于 一种 RISC-V VM，试图模拟 riscv32i 标准。BitVM 支持 20 条指令：ADD、SUB、MUL、AND、OR、XOR、ADDI、SUBI、ANDI、ORI、XORI、JMP、BEQ、BNE、RSHIFT1、SLTU、SLT、SYSCALL、LOAD 和 STORE。指令集确实充足以运行，例如 Turing 完全机器。

• 这包括逻辑和流控制，如 JMP、BEQ、BNE。特别是，记住 Bitcoin 脚本运行的是一个栈式机器。可以利用这一点来进行函数调用。
• 基本的算术操作在 u32 上已经在 Bitcoin 脚本中被模拟。注意，使用 SLTU 时，可以模拟 u64 整数操作，如 RISC Zero 的 VM。
• 还有可寻址内存。

每个 RISC-V CPU 循环都可以在 Bitcoin 脚本中重新运行/挑战。

挑战者可以通过展示在执行的特定 RISC-V CPU 循环中发生以下六个事件之一（即“欺诈”）来挑战 BitVM 中的执行。

• 故障的当前程序计数器
• 故障的下一程序计数器
• 故障的指令
• 故障的操作数 1 的读取
• 故障的操作数 2 的读取
• 故障的写入

如果没有挑战者能够挑战任何循环，那么根据欺诈证明的定义，执行必须正确。挑战者可以通过本地运行相同的 BitVM 程序以及一些输入数据，并参与挑战-响应游戏，指出 Bitcoin 网络上的差异。

这因此提供了一个非常简单的策略，如下所示。

• 将验证者编译为 BitVM 的 RISC-V 方言，这可能重用定制 RISC-V 的现有工作，Valida LLVM compiler。
• 创建 BitVM 执行声明作为一个 taproot 并将其发布到链上。
• 该 taproot 现在准备好被挑战。

注意，在 BitVM 的情况下，比特币友好的定义现在完全不同。以前，我们想确保验证者足够小且在 Bitcoin 脚本中效率足以进行验证，特别是它需要适应所有栈限制和重量单位限制。

这些对 BitVM 现在而言不再重要。实际上，由于跟踪的证明生成可以相当高效并能够并行化，因此证明生成的成本不再是关注点。然而，提交挑战的成本几乎是恒定的。BitVM 不必使用 OP_CAT，但在没有 OP_CAT 的情况下，开销将非常高，因为与哈希函数相关的开销将大大增加。

然而，BitVM 并非没有开销。像乐观 Rollup 一样，证明需要一个撤回期，以允许挑战者介入。请注意，完全链上的挑战-响应可能需要在证明者（称为 Paul）和挑战者（称为 Vicky）之间进行数十次往返，并且由于比特币的块时间为 10 分钟，这可能会需要相当长的时间。如果许多挑战者希望同时挑战，以及是否会影响延迟和最终性，这一点也不太明确。

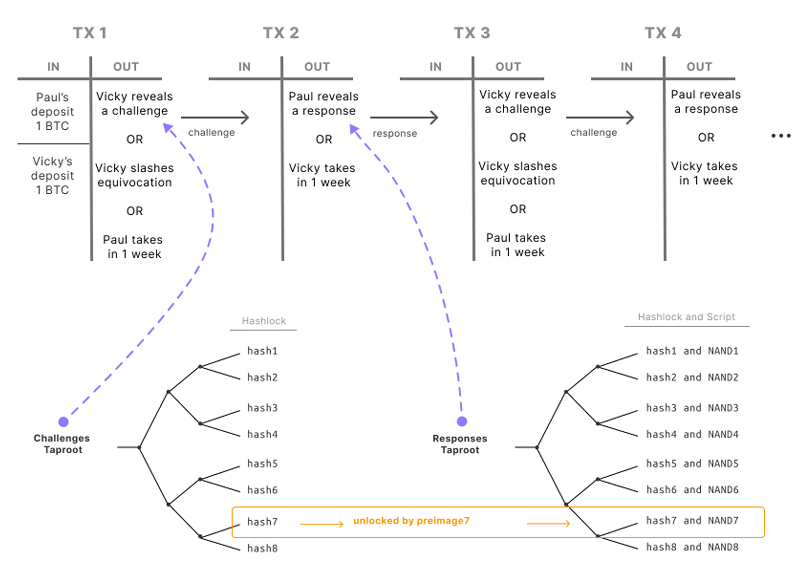
然而，以太坊中的许多乐观 Rollup 的撤回期为 7 天，因此仍有足够的时间进行挑战-响应，但这不适用于需要短撤回期的用例。我们还需要确保多个挑战者能够独立并行地工作。这可以防止某个拖延的挑战者阻碍其他认真的挑战者，并避免证明者在处理多个挑战者时需要额外的安全存款。

最近降低撤回期影响的解决方案是使用 EigenLayer 和 Babylon 等重新抵押协议，以招募验证者预先验证证明并宣布结果。AltLayer 一直在努力提供一揽子解决方案。这在实践中有效，但确实带来了额外假设。

我们密切关注 BitVM 的发展。作为一种通用的 RISC-V VM，BitVM 可能有助于促进比特币网络中可编程性的开发。BitVM 仍在开发中，但我们认为整体思路是有意义的——它的非交互式和近似对手，RISC Zero 或 Valida 已被实践投入使用。

证明聚合层

人们特别是比特币核心用户担心，一个日益增长的比特币应用数量将超负荷比特币的资源——尤其是在 Taproot 升级后，显著放宽了脚本大小限制。

在比特币社区中，有努力和活动旨在限制对比特币网络资源的不良使用。一个名为 “在 2023 年 2 月发生了什么？” 的网站代表了一个社区提案，建议节点自愿过滤某些交易，特别是由于铭文和 BRC-20 产生的交易，视为垃圾邮件。

尽管在比特币上验证 ZK 证明不太可能被归类为垃圾邮件，因为它确实是有用的，但如果有十几个应用程序频繁提交 ZK 证明进行验证，这可能会导致网络拥堵。去年报道称，比特币内存池在高峰时包含 194,374 笔交易。这是令人不快的，因为当交易处于内存池中时，这意味着该交易未能结算到比特币区块链。要么该交易必须支付更高的费用，要么则只能继续等待。

因此，在我们规划比特币上的 ZK 证明验证时，试图控制可能会带入比特币网络的开销是一个重要的设计考虑。

我们提出添加一个证明聚合层的想法。通过这个聚合层，不同的应用程序可以将它们的证明“组合”在一起，向比特币网络提交一个单一证明。这有很多好处。

• 它降低了比特币网络验证 ZK 证明的整体成本，这个成本可以低至只有一个应用程序出现时的成本。
• 它降低了不同应用使用比特币网络的成本，允许它们在成本和发布频率之间更好地进行权衡，通过能够在应用之间分摊成本。
• 如果使用了欺诈证明，它帮助挑战者，因为所有挑战者只需挑战一个欺诈证明即可涵盖所有应用。

在以太坊生态系统中，有几个项目正在研究证明聚合——在以太坊上，解决 ZK 证明的成本同样较高。这包括 Nebra 和 Aligned Layer。

当 ZK 准备好时，它可能通过提供一个可验证的去中心化存储层来帮助缓解比特币的网络压力，就像 Celestia 和 Nubit 希望做的那样。Nubit 使用以下架构，利用比特币进行抵押，以使存储层去中心化，而不是将数据上传到比特币网络。ZK 证明在这里可能会很有帮助，因为它们可以确保存储节点诚实地存储数据，并可以强制执行利益和惩罚机制，以便使存储层去中心化和可靠。

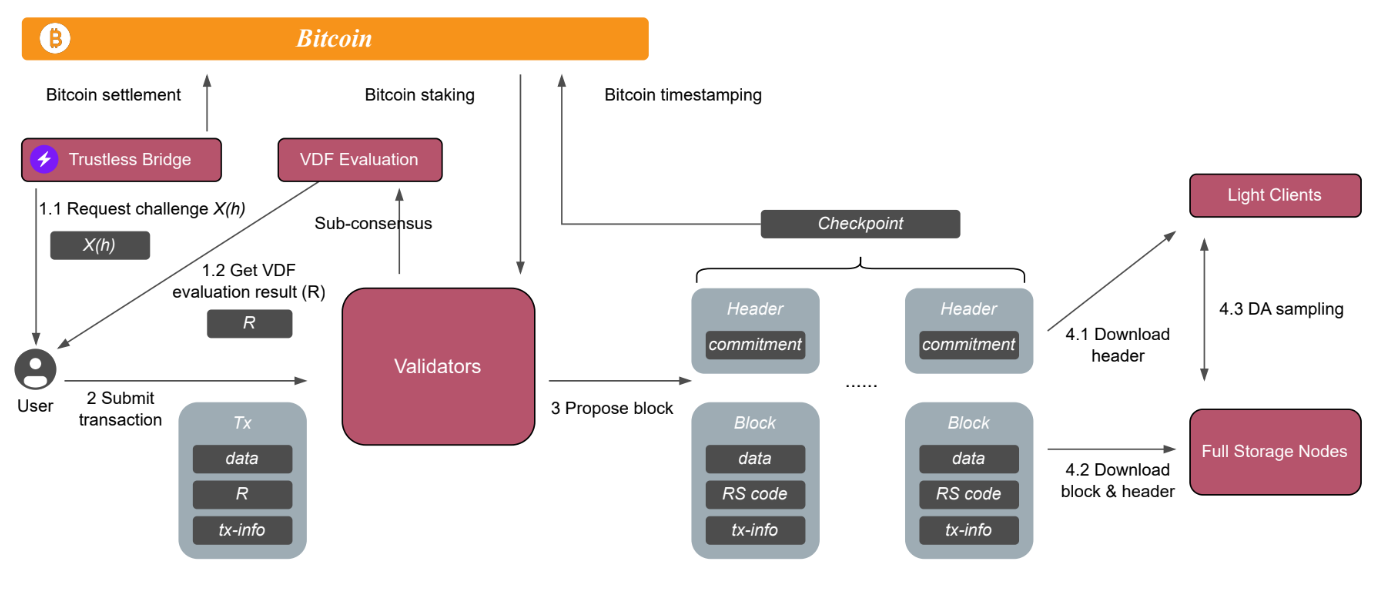
这可以用于欺诈证明和乐观 Rollup 的数据可用性，对于这种情况下，数据可用性仅需要是临时的而非永久性，并且它不应在比特币上用于存储。这也可以帮助 BRC20 和其他铭文协议，使其不必在比特币网络上发布数据，从而解决比特币社区的重大顾虑。

拥有一个由比特币共识通过 ZK 保护的数据可用性层，可以降低生成 BRC20 的成本，使 BRC-20 更加去中心化，并避免不必要的对比特币的开销。

工具和资源

比特币的未来依赖于开发者在其上进行构建，我们真诚地相信还有很多事情需要做，许多主题可以探索，很多应用可以构建。

对在比特币上构建可编程性感兴趣的人可以参考 BitVM 代码库。

• https://github.com/BitVM/BitVM

BitVM 团队也在工作一个 Rust 编程环境和工具包，用于处理比特币脚本。

使用 OP_CAT 来实现比特币中复杂功能的技术已经被 Blockstream 和其他公司所讨论。

• https://medium.com/blockstream/cat-and-schnorr-tricks-i-faf1b59bd298
• https://rusty.ozlabs.org/2023/10/20/examining-scriptpubkey-in-script.html

sCrypt，虽然依赖于 Bitcoin SV 但不依赖于比特币，能够提供有关如何使用 OP_CAT 和其他潜在操作码实现非常复杂特性的见解。

• https://scrypt.io/

许多项目与 Polyhedra 一起工作，以扩展比特币的模块化基础设施。

• Babylon: https://babylonchain.io/
• Syscoin: https://syscoin.org/
• Merlin Chain: https://merlinchain.io/
• Bitlayer: https://www.bitlayer.org/
• B² Network: https://www.bsquared.network/
• BEVM: https://www.bevm.io/
• LumiBit: https://lumibit.xyz/
• bitSmiley: https://www.bitsmiley.io/
• Particle Network: https://particle.network/

致谢

特别感谢来自 L2 Iterative 的 Weikeng Chen (https://www.l2iterative.com/)，作为 Polyhedra 网络的投资者和技术合作伙伴，以及来自伊利诺伊大学香槟分校的 Yupeng Zhang 在比特币生态系统和零知识证明领域的研究合作。

• 原文链接： hackmd.io/@l2iterative/b...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～