功能加密简介

原文：https://www.leku.blog/fe/ 作者：Enrico 译者：Kurt Pan

功能加密 (FE) 可以看作是对公钥加密 (PKE) 的推广, 允许对第三方的解密能力进行更细粒度的控制。

在公钥加密中，使用公钥$p_k$隐藏值$x$于密文（加密算法）而私钥$s_k$用于从$ct$中恢复（解密算法）。公钥加密实现的是"全有或全无"的访问规则——要么解密并读取整个明文，要么对明文一无所知。在功能加密中，密钥$sk_f$与特定函数$f$相关联，使得解密函数返回$f(x)$。将设置为恒等函数，就可以从功能加密导出公钥加密。

在这里你可以看到两种加密协议之间不同的"API"。功能加密的设置阶段生成主私钥$msk$，可以在密钥生成阶段使用它来导出对于特定$f$的私钥$sk_f$。加密算法遵循相同的逻辑, 而解密需要函数私钥$sk_f$以得到$f(x)$。

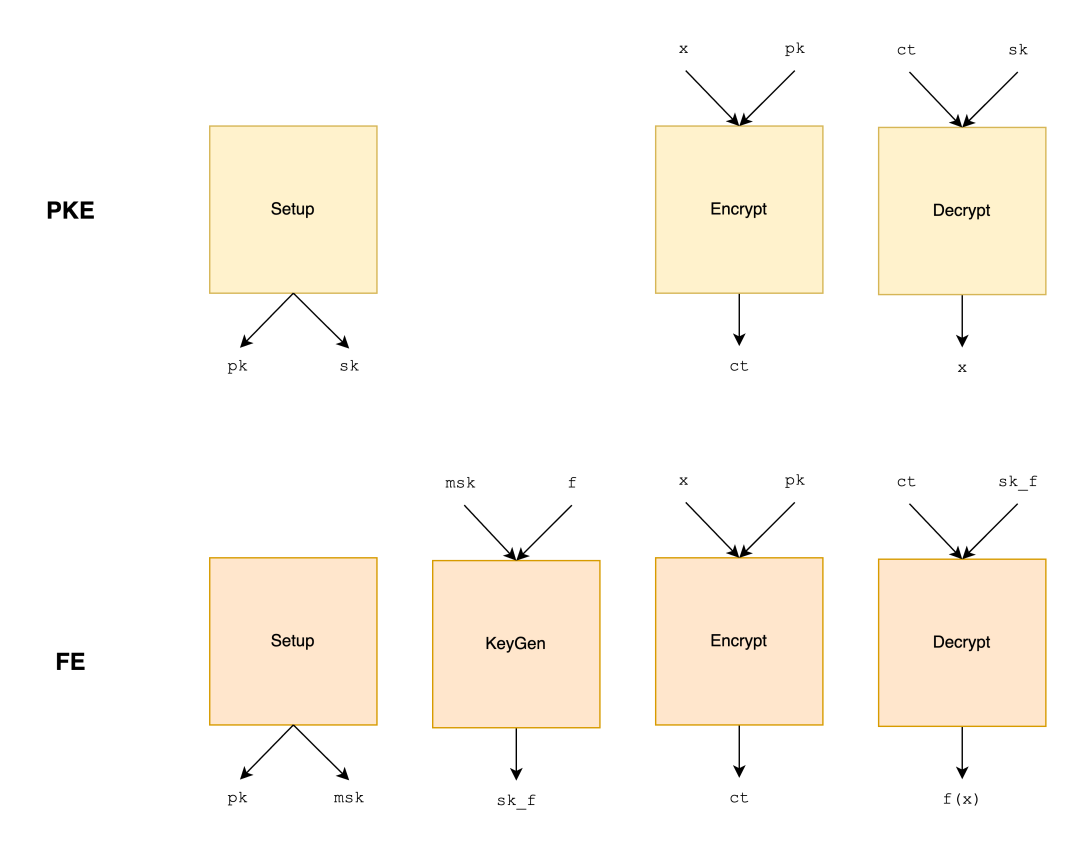
非形式化地，功能加密方案的安全性要求敌手相比$f(x)$所揭示的不获得更多关于的信息。[BSW10]提供了此类方案的更形式化的安全定义。稍后我也会尝试详细解释。现在，让我们通过考虑一个示例应用来巩固对这种加密方案的理解。

应用实例

考虑一家存有大量患者记录的医院, 且有$n$类对这些数据具有不同访问级别的专家类别。在这种情况下，医院管理部门将运行设置阶段，然后创建不同的函数密钥$sk_f1,...,sk_fi,...,sk_fn$，每个函数$f_i$对患者记录的特定访问策略进行编码。管理部门随后将密钥分发给相应的类别。患者记录被$pk$加密，每个专家都可以执行解密函数, 但仅披露他们被允许访问的信息, 而不会披露其他信息。

在这样的设置中, 管理部门生成可以服务于多个访问级别的单个加密记录。这比传统的对称/非对称加密更有效，传统的对称/非对称加密需要管理部门执行$n$次加密。

与全同态加密的差异

如果你熟悉全同态加密 (FHE)，那么分析这两个原语之间的差异和相似点可能会很有趣。两者都允许对加密数据执行函数，但它们所服务的场景和用例截然不同。通常，全同态加密的应用专为外包计算而设计，使得：

• Alice 执行设置并加密她的数据$x$并发送生成的密文 给Bob。
• Bob 在密文上$ct$求值函数 ，获得$ct'$并将结果发送给Alice。
• Alice 解密密文并得到$f(x)$。

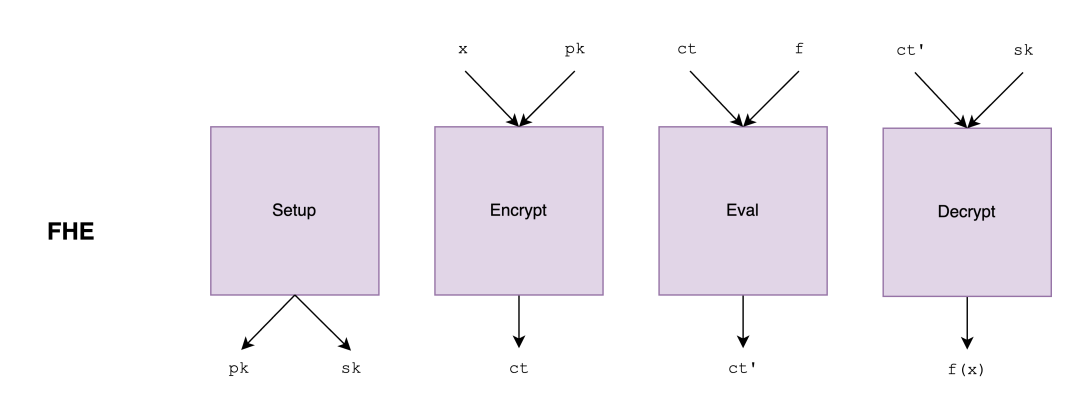
在全同态加密中，对加密数据执行的函数$f$（求值阶段）是任意的：Bob 可以在密文$ct$上应用任意算术函数，甚至可以是对 Alice 私有的。相反，在功能加密中，可以对密文执行的函数集受到由主参与方生成的函数密钥的限制。另一方面，全同态加密求值函数返回另一个密文，需要Alice的干预才能解密。在功能加密中，无需进一步交互即可访问$f(x)$，因为求值和解密功能是同时执行的。

简言之, 全同态加密始终需要与密钥所有者进行交互才能获得$f(x)$，但函数$f$可以是任意的（并且可选地可以是秘密的)。在功能加密中, 无需与密钥所有者交互即可获得$f(x)$，但可以执行的函数集是有限的。

功能加密的安全定义

功能加密的安全性是根据选择明文攻击（IND-CPA）下的不可区分性的概念来定义的。安全性通过敌手和挑战者之间的博弈来证明。博弈的逻辑类似于用于证明公钥加密方案的语义安全性的逻辑，如下所示。 

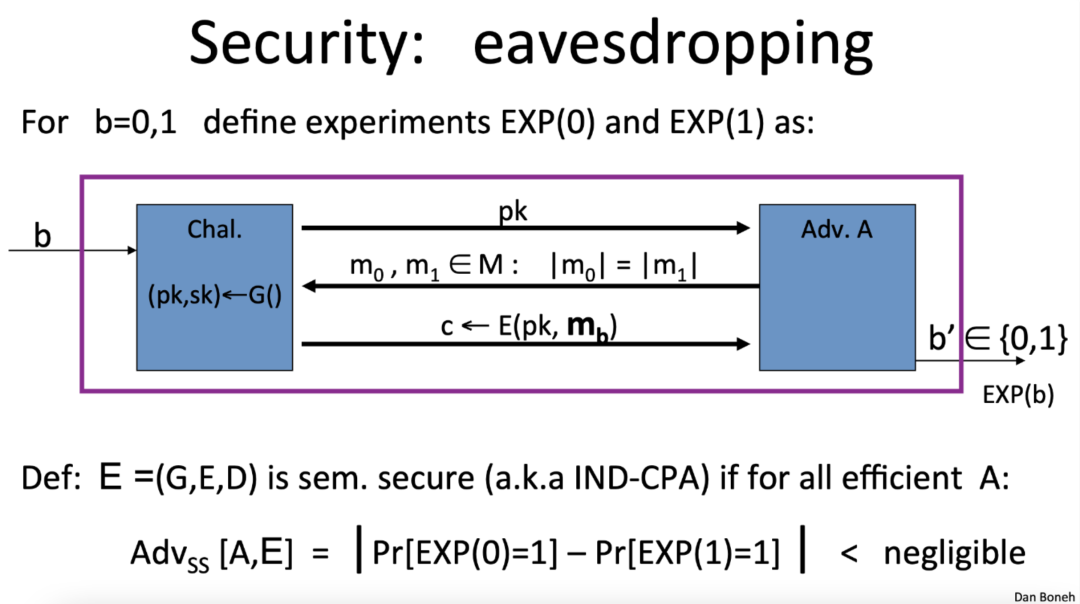
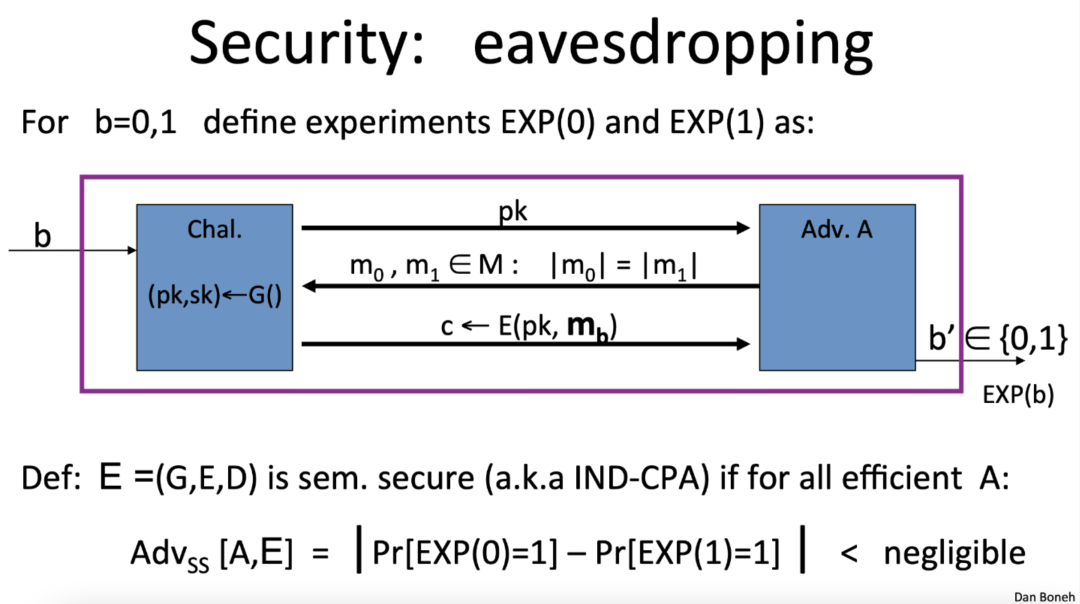我们先来分析公钥加密的情况。对 , 实验 的过程如下:

• 挑战者使用函数$G()$生成密钥对 , 并将$(pk,sk)$给$A$。
• $A$接收公钥$pk$。
• $A$选择两条长度相同的消息$m_0$和$m_1$, 并与挑战者共享。
• 挑战者使用公钥$pk$加密消息$m_b:c \leftarrow E(pk,m_b)$，其中$B$为 0 或 1 ，但$A$不知道其值。
• $A$收到密文$c$并输出一个猜测$b'\in {0,1}$

由函数$(G,E,D)$定义的方案$E$在是语义安全的，如果不存在高效的（多项式时间）敌手$A$能够区分对$m_0$和$m_1$的加密。使用数学, 这表示为: $|Pr[EXP(0) = 1] - Pr[EXP(1) = 1]| < negligible$ 其中，$Pr[EXP(0) = 1]$表示敌手在实验 0 中错误地输出 1 的概率，$Pr[EXP(1) = 1]$表示敌手在实验 1 中正确地输出 1 的概率。换句话说，敌手正确猜测哪条消息被加密的概率应该非常接近随机猜测的概率。实际上，这确保了敌手无法通过查看密文来了解明文的任何信息，即使他可以选择要加密的消息。正如 Morrolan 所指出的，当且仅当加密方案是非确定性的，即同一公钥下对同一明文的两次加密必须以极大概率产生不同的密文时，此安全性质才成立。

• https://crypto.stackexchange.com/questions/100361/security-definition-for-ind-cpa-of-public-key-encryption

在功能加密 (FE) 中, 博弈略有不同。对$b = 0,1$, 实验 的过程如下:

• 挑战者生成密钥对$(pk,msk)$。
• $A$自适应地向挑战者提交不同函数$f_1,f_2,...,f_i$的查询，并接收相应的函数私钥$sk_f1,sk_f2,...,sk_fi$
• $A$选择两条消息$m_1$和$m_2$, 使得$f_i(m_1) = f_i(m_2)$, 并与挑战者共享。
• 挑战者使用公钥$pk$加密消息$m_b:c \leftarrow E(pk,m_b)$，其中$b$为 0 或 1，但$A$不知道其值。
• $A$收到密文$c$并输出一个猜测$b' \in {0,1}$。

敌手能够解密密文$c$并获得$f(m_b)$，但是，与之前类似，无法区分密文$c$是$m_1$还是$m_2$的加密。这证明了引言中给出的安全性定义。更精确地说， [BSW10] 表明此安全性定义对于特定的函数$f$来说是不充分的, 并在论文中提供了一个更严格的安全定义。

结论

正如本文所述，除了与加密数据计算的实际应用相关之外，功能加密已被证明是理论密码学中的强大工具，可用于构造高级原语，例如不可区分混淆 (iO) ：由于它能够实例化几乎所有已知的密码学原语，因此被认为本质上是“密码学完备的”。特别地，根据Sora的演示，iO可以使用递归功能加密构造。功能加密的实际构造，请见后续博文。

• https://speakerdeck.com/sorasuegami/ideal-obfuscation-io

参考

• [BSW10]：https://eprint.iacr.org/2010/543.pdf