备战后量子:格密码学初学者指南
- XPTY
- 发布于 2025-05-10 17:41
- 阅读 3011
保护网路安全的密码学技术正不断发展,是时候赶上进度了。这篇文章是关于格密码学的教程,格密码学是后量子(PQ)转变的核心范式。
<!--StartFragment-->
原文:https\://blog.cloudflare.com/lattice-crypto-primer/
作者:Christopher Patton,Peter Schwabe
译者:Kurt Pan
 保护网路安全的密码学技术正不断发展,是时候赶上进度了。这篇文章是关于格密码学的教程,格密码学是后量子(PQ)转变的核心范式。
保护网路安全的密码学技术正不断发展,是时候赶上进度了。这篇文章是关于格密码学的教程,格密码学是后量子(PQ)转变的核心范式。
十二年前(2013 年),美国大规模监控事件的曝光引发了 TLS 在网路加密和认证方面的广泛应用。这一转变得益于基于椭圆曲线的新型、更高效的公钥密码学的标准化和实现。椭圆曲线密码学比其前身(包括有限域上的 RSA 和 Diffie-Hellman)更快,且需要的通讯更少。
如今向 PQ 密码学技术的转变可以解决 TLS 及其他领域面临的一个迫在眉睫的威胁:一旦建成,足够大的量子电脑就可以用来破解目前使用的所有公钥密码学。我们不断看到量子电脑工程的进步,这个威胁距离成为现实越来越近。
幸运的是,这一转变正在顺利进行中。学界和标准界花了数年时间开发抵抗量子密码分析的替代方案。就其本身而言,Cloudflare 也为这一进程做出了贡献,且是新开发方案的早期採用者。事实上,PQ 加密自 2022 年起就已在我们的边缘装置上使用,目前(2025 年)已有超过 35% 的非自动化 HTTPS 流量採用该加密。今年,我们开始大力推动 TLS 生态系统的 PQ 认证。
- https\://blog.cloudflare.com/post-quantum-for-all/
- https\://radar.cloudflare.com/adoption-and-usage#post-quantum-encryption-adoption
基于格的密码学是第一个取代椭圆曲线的范式。除了 PQ 安全性之外,就 CPU 时间而言,格通常会同样快,有时甚至更快。然而,这种公钥加密的新范式有一个主要代价:格比椭圆曲线需要更多的通讯。例如,使用格建立加密密钥需要客户端和伺服器之间进行 2272 位元组的通讯(ML-KEM-768),而使用基于现代椭圆曲线的方案(X25519)进行密钥交换仅需 64 位元组。承担这样的成本需要大量的工程,从处理 TCP 封包碎片到重新设计 TLS 及其公钥基础架构。因此,PQ 转换将需要大量具有不同背景的人员的参与,而不仅仅是密码学家。
- https\://csrc.nist.gov/pubs/fips/203/final
- https\://datatracker.ietf.org/doc/html/rfc7748
- https\://blog.cloudflare.com/sizing-up-post-quantum-signatures/
- https\://blog.cloudflare.com/pq-2024/#two-migrations
这篇文章的主要读者是那些参与 PQ 转型并希望更好地了解幕后情况的人。然而,更根本的是,我们认为每个人在某种程度上理解格密码学是很重要的,特别是如果我们相信它能保证我们的安全和隐私。
我们假设你具有软体工程背景,且熟悉 TLS、加密和认证等概念。我们将看到,格密码学背后的数学至少在最高层次上并不难掌握。具有加密工程背景并希望深入了解的读者可能希望从 Vadim Lyubashevsky 的优秀教程开始,本博文就是基于该教程撰写的。我们也推荐 Sophie Schmieg 关于这个主题的部落格。
- https\://eprint.iacr.org/2024/1287
- https\://keymaterial.net/2023/09/01/learning-but-with-errors/
虽然向格密码学的转变会产生成本,但也创造了机会。我们可以用椭圆曲线构建的许多东西也可以用格构建,儘管效率并不总是那麽高;但是我们也可以用格来做一些我们不知道如何用其他东西来有效地做的事情。我们将在最后讨论其中的一些应用程式。
我们将在这篇文章中讨论很多内容。如果你坚持下去,我们希望你能够感受到些许力量,不仅对能够应对 PQ 转型所带来的工程挑战,也关于能够解决你以前不知道如何解决的问题。
请繫好安全带--让我们玩得开心!
加密
PQ 转型最迫切的问题是确保未来的量子电脑不会破解今天的加密。如今,攻击者可以储存你的笔记型电脑和你造访的网站之间交换的资料包,然后在未来的某个时间使用量子电脑解密这些资料包。这意味着当今互联网上传输的大部分敏感资讯——从 API 令牌和口令到资料库加密密钥——有一天都可能会被量子电脑解锁。
- https\://blog.cloudflare.com/https-only-for-cloudflare-apis-shutting-the-door-on-cleartext-traffic/
事实上,现今 TLS 中的加密大多是 PQ 安全的:存在风险的是浏览器和伺服器建立加密密钥的过程。 目前,这通常是採用基于椭圆曲线的方案来实现的,但这些方案并不具备 PQ 安全性;本节的目标是了解如何使用基于格的方案进行密钥交换。
我们将研究并实现 ML-KEM(又称 Kyber)的简化版本,这是当今使用最广泛的 PQ 密钥交换。我们的程式码效率和安全性当然不如一个符合规范、生产品质的实现,但会足以掌握主要思想。
- https\://pkg.go.dev/github.com/cloudflare/circl\@v1.6.0/kem/mlkem
密钥交换的协议。对于那些不熟悉 DH 的读者来说,目标是让 Alice 和 Bob 透过不安全的网路建立共享秘密。为此,双方各自选择一个随机秘密数字,计算相应的“密钥份额”,并将该密钥份额发送给对方:
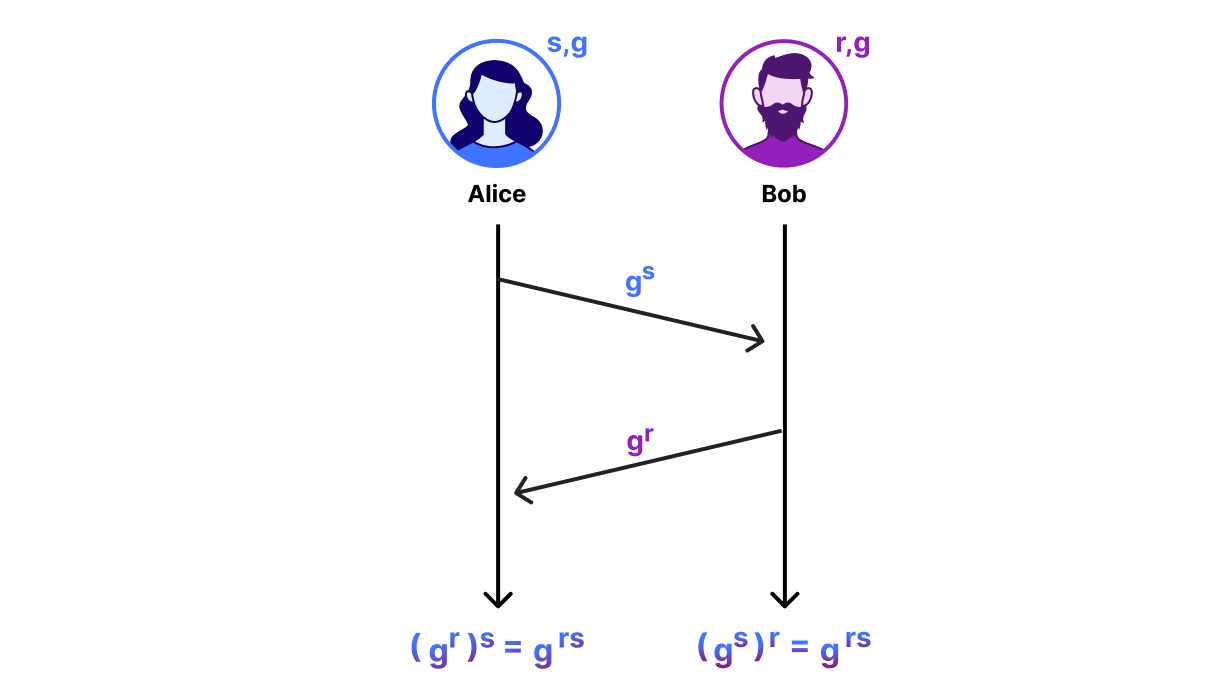
Alice 的秘密数字是 ,她的密钥份额是 ; Bob 的秘密数字是 ,他的密钥份额是 。然后,给定他们的秘密和对方的密钥份额,每个人都可以计算 。这个协议的安全性来自于我们如何选择 、 和 以及如何进行算术运算。 DH 最高效的实例化会使用椭圆曲线。
在 ML-KEM 中,我们用矩阵运算取代椭圆曲线上的运算。它不是简单的替换,所以我们需要一点线性代数来理解它。但别担心:我们将使用 Python,因此我们有可运行程式码供使用,我们将使用 NumPy 来保持高抽象层级。
我们需要的所有数学知识
矩阵只是一个二维数组。在 NumPy 中,我们可以如下建立矩阵(将 numpy 引入为 np ):
A = np.matrix([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])这将 A 定义为 3 × 3 矩阵,其项为 A[0,0]==1, A[0,1]==2, A[0,2]==3, A[1,0]==4 ,依此类推。
就本文目的而言,我们的矩阵的项将始终是整数。此外,每当我们对两个整数进行加、减或乘运算时,我们都会约减结果,就像我们对时钟上的小时数进行的一样,这样我们最终会得到某个正数 Q 的 range(Q) 中的数字,这个数字称为模数。现在确切的值并不重要,但对于 ML-KEM 来说它是 Q=3329 ,所以我们现在就使用这个值。 (时钟的模数为 Q=12 。)
在 Python 中,我们将整数 a 和 b 模 Q 的乘法写成 c = a*b % Q 。这里我们计算 a*b ,将结果除以 Q ,然后将馀数赋值给 c 。例如, 42*1337 % Q 等于 2890 而不是 56154 。模加法和模减法以类似的方式进行。对于本部落格的其馀部分,当上下文清楚地表明我们指的是模运算时,我们有时会省略「 % Q 」。
接下来,我们需要对矩阵进行三种运算。
第一个是矩阵转置,在 NumPy 写作 A.T 。此运算沿着矩阵的对角线翻转,使得所有行 i 和列 j 均为 A.T[j,i] == A[i,j] :
print(A.T)
# [[1 4 7]
# [2 5 8]
# [3 6 9]]为了形象化地展示这一点,想像在一张半透明的纸上写下一个矩阵。从纸张的左上角到右下角画一条线,然后围绕该线将纸张旋转 180°:
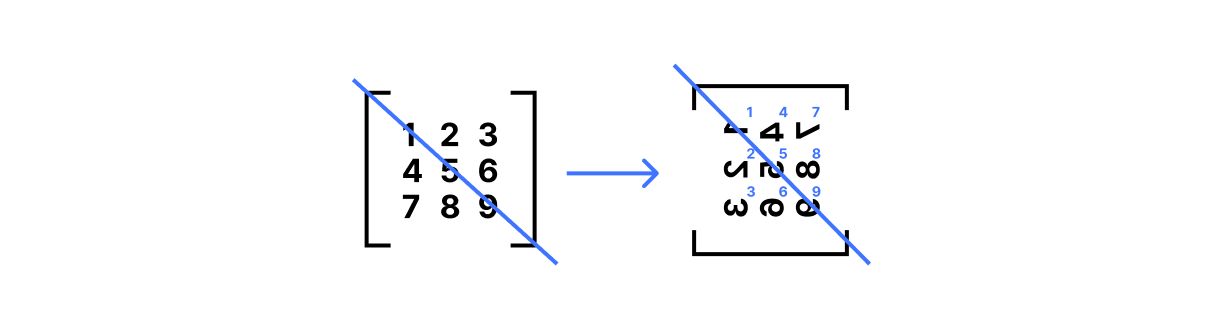
我们需要的第二个运算是矩阵乘法。通常,我们会将一个矩阵乘以一个列向量,这只是一个只有一列的矩阵。例如,以下 3 × 1 矩阵是一个列向量:
s = np.matrix([[0],
[1],
[0]])我们也可以将 s 更简洁地写成 np.matrix([[0,1,0]]).T 。为了将方阵 A 与列向量 s 相乘,我们计算 A 的每一行与 s 的点积。也就是说,如果是 t = A*s % Q ,那麽对于每一行 i ,则为 t[i] == (A[i,0]*s[0,0] + A[i,1]*s[1,0] + A[i,2]*s[2,0]) % Q 。输出始终是一个列向量:
print(A*s % Q)
# [[2]
# [5]
# [8]]此列向量的行数等于左侧矩阵的行数。具体来说,如果我们取列向量 s ,将其转置为 1 × 3 的矩阵,并将其乘以 3 × 1 的矩阵 r ,那麽我们最终会得到 1×1 的矩阵:
r = np.matrix([[1,2,3]]).T
print(s.T*r % Q)
# [[2]]我们需要的最后一个矩阵运算是矩阵加法。如果 A 和 B 都是 N × M 矩阵,则 C = (A+B) % Q 就是 N × M 矩阵,且 C[i,j] == (A[i,j]+B[i,j]) % Q 成立。当然,只有当我们相加的矩阵具有相同的维度时,这才有效。
预热
数学讲得够多了——让我们开始交换一些密钥。我们从先前的 DH 图开始,用矩阵运算取代之前的计算。请注意,该协议并不安全,但将成为我们在下一节中开发的安全密钥交换机制的基础:
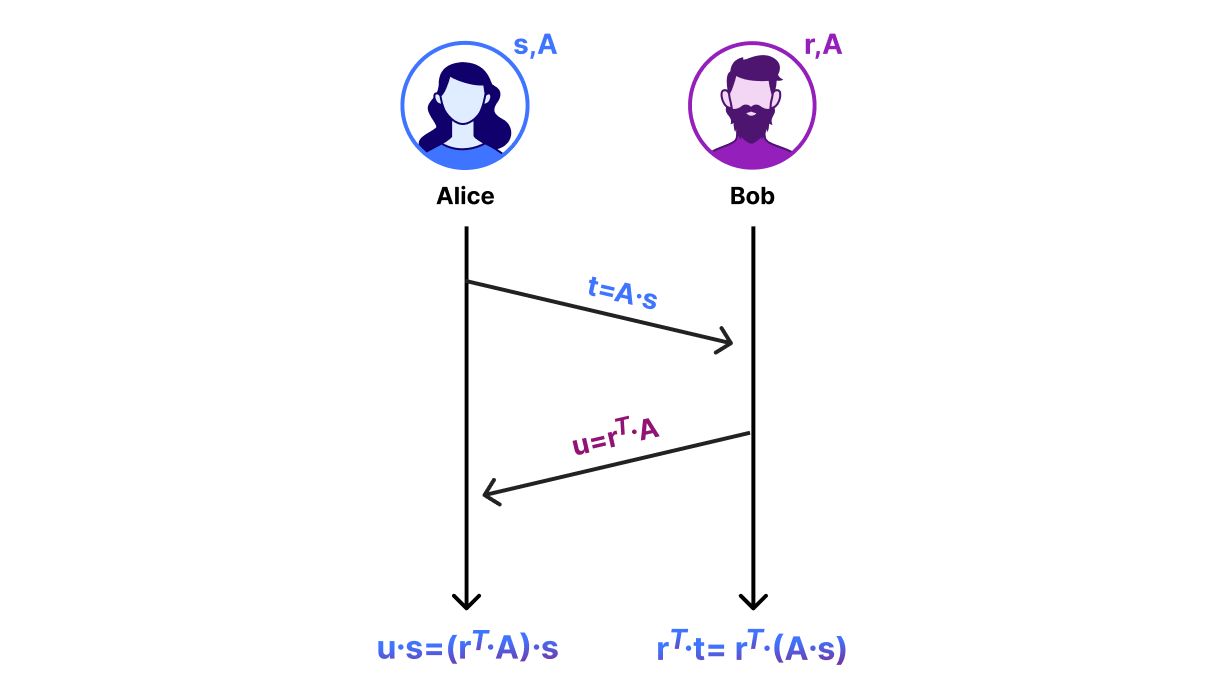
- Alice 和 Bob 就一个公开的
N×N矩阵A达成一致。这类似于 Alice 和 Bob 在 DH 图中同意的数字 g 。 - Alice 选择一个随机长度
N的向量s并将t = A*s % Q传送给 Bob。 - Bob 选择一个随机长度
N的向量r并将u = r.T*A % Q传送给 Alice。你也可以将其计算为(A.T*r).T % Q.
向量 t 和 u 类似于 DH 密钥份额。交换这些密钥份额之后,Alice 和 Bob 可以计算出一个共享秘密。 Alice 将共享秘密计算为 u*s % Q ,Bob 将共享秘密计算为 r.T*t % Q 。要了解为什麽它们计算出相同的密钥,注意到 u*s == (r.T*A)*s == r.T*(A*s) == r.T*t.
事实上,这种密钥交换本质上就是 ML-KEM 中发生的事情。但是,我们不是直接使用它,而是将其作为公钥加密方案的一部分。公钥加密包括三种演算法:
key_gen():输出公钥加密密钥pk和对应的秘密解密私钥sk的密钥产生演算法。encrypt():输入公钥和明文并输出密文的加密演算法。decrypt():输入密钥和密文并输出底层明文的解密演算法。也就是说,对任何明文ptxt,都有decrypt(sk, encrypt(pk, ptxt)) == ptxt。
如果给定密文和用于加密它的公钥,攻击者在不知道私钥的情况下无法辨别有关底层明文的任何信息,则我们可以说该方案是安全的。一旦我们有了这个加密方案,我们就可以在最后一步将其转换为密钥封装机制(「ML-KEM」中的「KEM」)。 KEM 与加密非常相似,只是明文始终是随机产生的密钥。
我们的加密方案如下:
key_gen():为了产生密钥对,我们选择一个随机方阵A和一个随机列向量s。我们将公钥设定为(A,t=A*s % Q),将私钥设定为s。请注意,t是上述密钥交换协议中 Alice 的密钥份额。encrypt():假设我们的明文ptxt是range(Q)中的一个整数。为了加密ptxt,Bob 产生了他的密钥份额u。然后,他导出共享秘密并将其添加到ptxt中。密文有两个组成部分:
u = r.T*A % Q
v = (r.T*t + m) % Q
这里 m 是一个包含明文的 1 × 1 矩阵,即 m = np.matrix([[ptxt]]) ,而 r 是一个随机列向量。
decrypt():为了解密,Alice 计算共享密钥并将其从v中减去:
m = (v - u*s) % Q
有些读者会注意到,这看起来很像 El Gamal 加密。这并非巧合。优秀的密码学家会制定自己的密码;伟大的密码学家从优秀的密码学家那里窃取密码。
现在让我们将其整合成程式码。我们最后需要的是一种产生随机矩阵和列向量的方法。下面我们将此函数称为 gen_mat() 。尝试自己实现这一点。我们的方案有两个参数:模数 Q ;以及矩阵和列向量的维数 N 。 N 的选择对于安全性很重要,但现在你可以随意选择你想要的值。
def key_gen():
# 这里 `gen_mat()` 返回一个N×N的矩阵
# 其项随机从`range(0, Q)`中选取
A = gen_mat(N, N, 0, Q)
# 除了矩阵是 N×1,同上
s = gen_mat(N, 1, 0, Q)
t = A*s % Q
return ((A, t), s)
def encrypt(pk, ptxt):
(A, t) = pk
m = np.matrix([[ptxt]])
r = gen_mat(N, 1, 0, Q)
u = r.T*A % Q
v = (r.T*t + m) % Q
return (u, v)
def decrypt(sk, ctxt):
s = sk
(u, v) = ctxt
m = (v - u*s) % Q
return m[0,0]
# 测试
assert decrypt(sk, encrypt(pk, 1)) == 1让方案安全(或「什麽是格?」)
现在,你可能想知道格到底是什麽。我们保证会对其进行定义,但在此之前,先了解为什麽我们的预热方案不安全以及如何修復之,会有所帮助。
熟悉线性代数的读者可能已经看到了这个问题:为了确保方案的安全,攻击者应该不可能恢復密钥 s ;但给定公开的 (A,t) ,我们可以立即使用高斯消元法来求解 s 。
更具体地说,如果 A 可逆,我们可以将私钥写成 A^{-1}*t == A^{-1}*(A*s) == (A^{-1}*A)*s == s, ,其中 A^{-1} 是 A 的逆。 (当将一个矩阵乘以其逆时,会得到单位矩阵 I ,它只是将列向量乘以自身,即 I*s == s. )我们可以用高斯消元法来计算这个矩阵。直观地说,我们所做的就是求解一组线性方程,其中 s 的项是未知变数。 (请注意,即使 A 不可逆,这也可能。)
为了确保这个加密方案的安全,我们需要让它变得有点…「混乱」。
让我们变得混乱
首先,我们需要让从公钥恢復私钥变得困难。让我们尝试以下操作:产生另一个随机向量 e 并将其加到 A*s 中。我们的密钥产生演算法变成:
def key_gen():
A = gen_mat(N, N, 0, Q)
s = gen_mat(N, 1, 0, Q)
e = gen_mat(N, 1, 0, Q)
t = (A*s + e) % Q
return ((A, t), s)我们的公钥列向量分量公式 t 现在包含一个加法项 e ,我们称之为错误。与密钥一样,错误只是一个随机向量。
注意,先前的攻击不再有效:因为 A^{-1}*t == A ^{-1} *(A*s + e) == A ^{-1} *(A*s) + A ^{-1} *e == s + A ^{-1} *e ,我们需要知道 e 才能计算 s 。
很好,但是这个补丁又产生了另一个问题。花一点时间将这个新的密钥产生演算法插入到你的实作中并进行测试。会发生什麽事?
你应该会看到 decrypt() 现在输出的是垃圾讯息。我们可以用一些代数来解释下原因:
(v - u*s) == (r.T*t + m) - (r.T*A)*s
== r.T*(A*s + e) + m - (r.T*A)*s
== r.T*(A*s) + r.T*e + m - r.T*(A*s)
== r.T*e + m
r 和 e 的项是随机取样的,因此 r.T*e 也是均匀随机的。就好像我们用一次一密加密了 m ,然后又把一次性密码本丢掉了!
处理解密错误
我们能做些什麽呢?首先,如果 r.T*e 很小,解密就会产生接近明文的结果,这会很有帮助。想像一下,我们可以产生 r 和 e ,使得对于某个小的 epsilon , r.T*e 位于 range(-epsilon, epsilon+1) 中。然后 decrypt 会在 range(ptxt-epsilon, ptxt+epsilon+1) 中输出一个数字,该数字与实际的明文非常接近。
然而,我们需要做的不仅仅是接近。想像一下,由于解密错误,你的浏览器有三分之一的时间无法载入你最喜欢的网站。没人有时间做那事。
ML-KEM 透过巧妙地对明文进行编码来降低解密错误的机率。假设我们要做的只是加密一位,即 ptxt 是 0 或 1 。考虑 range(Q) 中的数字,并将数字线分成四个大致相等长度的区块:
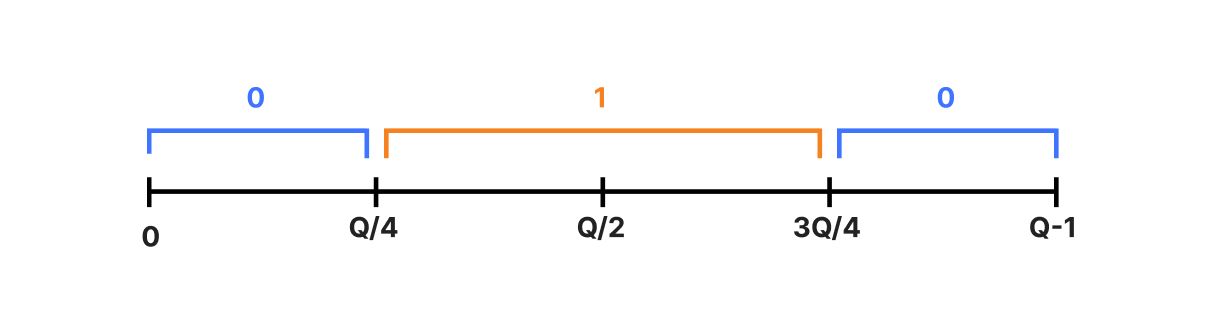
这里我们用 ptxt=0 标记了零附近的区域( -Q/4 到 Q/4 模 Q ),用 ptxt=1 标记了远离零的区域。为了对位元进行编码,我们将其设定为与其范围中间对应的整数,即 m = np.matrix([[ptxt * Q//2]]) 。 (注意双精确度「 // 」—这表示 Python 中的整数除法。)为了解码,我们选择与 m[0,0] 所在范围相对应的 ptxt 。这样,如果解密错误很小,那麽我们很有可能最终处于正确的范围内。
现在剩下的就是确保解密错误 r.T*e 很小。我们透过对短向量 r 和 e 进行取样来实现这一点。我们所说的「短」是指这些向量的项是从比 range(Q) 小得多的范围内採样的。具体来说,我们将选择一些小的正整数 beta 和样本项 range(-beta,beta+1) 。
我们如何选择 beta ?嗯,它应该足够小,以便解密以压倒性概率成功,但又不能太小,以至于 r 和 e 很容易被猜到,从而导致我们的方案被破解。花一两分钟来玩一下这个。我们可以改变的参数是:
- 模数
Q - 列向量的维数
N - 短性参数
beta
这些参数的哪些范围会导致解密错误率低但秘密向量难以猜测?就运行时间和通讯成本(公钥加上密文的大小)而言,我们的方案在哪些范围内最有效?我们将在本节末给出具体的答案,但同时,我们鼓励你稍微尝试一下。
高斯的反击
此时,我们有一个可行的加密方案,可以缓解至少一次密钥復原攻击。我们已经取得了很大进展,但至少还有一个问题。
再看密文 ctxt = (u,v) 的公式。如果我们设法恢復随机向量 r 会发生什麽?这将是灾难性的,因为 v == r.T*t + m ,而我们已经知道 t (公钥的一部分)和 v (密文的一部分)。
正如我们能够在初始方案中根据公钥计算出私钥一样,我们可以使用高斯消元法从密文分量 u 中恢復加密随机性 r 。再说一次,这只是因为 r 是线性方程组的解。
我们可以像以前一样透过添加一些噪音来缓解这种明文恢復攻击。具体来说,我们将根据 gen_mat(N,1,-beta,beta+1) 产生一个短向量并将其添加到 u 中。我们还需要以相同的方式向 v 添加噪声,原因我们将在下一节讨论。
再一次,新增噪声会增加解密错误的机率,但这次错误的大小也取决于私钥 s 。为了理解这一点,回想一下在解密过程中,我们将 u 乘以 s (以计算共享秘密),并且误差向量是一个加法项。因此,我们也需要 s 作为一个短向量。
现在让我们将所学到的一切整合成一个更新的加密方案。我们的方案现在有三个参数, Q , N 和 beta ,可以用来加密单一位元:
def key_gen():
A = gen_mat(N, N, 0, Q)
s = gen_mat(N, 1, -beta, beta+1)
e1 = gen_mat(N, 1, -beta, beta+1)
t = (A*s + e1) % Q
return ((A, t), s)
def encrypt(pk, ptxt):
(A, t) = pk
m = np.matrix([[ptxt*(Q//2) % Q]])
r = gen_mat(N, 1, -beta, beta+1)
e2 = gen_mat(N, 1, -beta, beta+1)
e3 = gen_mat(1, 1, -beta, beta+1)
u = (r.T*A + e2) % Q
v = (r.T*t + e3 + m) % Q
return (u, v)
def decrypt(sk, ctxt):
s = sk
(u, v) = ctxt
m = (v - u*s) % Q
if m[0,0] in range(Q//4, 3*Q//4):
return1
return0
# 测试
assert decrypt(sk, encrypt(pk, 0)) == 0
assert decrypt(sk, encrypt(pk, 1)) == 1在继续之前,请尝试找到该方案适用的参数以及秘密和错误向量难以猜测的参数。
带错误学习
到目前为止,我们已经有一个有效的加密方案,并缓解了两种攻击,一种是密钥恢復攻击,另一种是明文恢復攻击。似乎没有其他明显的方法可以破解我们的方案,除非我们选择的参数非常弱,以至于攻击者可以轻松猜出密钥 或密文随机性 。再次强调,这些向量需要足够短以防止解密错误,但也不能太短到容易被猜到。 (对于误差项也是如此。)
儘管如此,可能还存在需要更複杂一些才能实施的其他攻击。例如,我们可以进行一些数学分析来恢復部分密文随机性,或至少对其进行很好的猜测。这就引出了一个更基本的问题:一般来说,我们要如何确定这样的密码系统其实是安全的?
作为第一步,密码学家喜欢尝试减少攻击面。现代密码系统的设计使得攻击方案的问题可以归约为解决其他更容易推理的问题。
我们的公钥加密方案很好地说明了这个想法。回想一下上一节中的密钥和明文恢復攻击。这些攻击有何共同点?
在这两种情况下,攻击者都知道一些公共向量,从而可以恢復秘密向量:
- 在密钥復原攻击中,攻击者知道
t对应A*s == t. - 在明文恢復攻击中,攻击者知道
u对应r.T*A == u(或者,等效地,A.T*r == u.T)。
两种情况下的解决方法都是以难以解出秘密的方式建构公共向量,即添加错误项。然而,理想情况下,公共向量不会透露任何有关秘密的资讯。这由 「带错误学习」(LWE) 问题形式化。
LWE 问题要求攻击者区分两个分佈。具体来说,假设我们抛一枚硬币,如果出现正面,我们就从第一个分佈中抽取样本,并将样本交给攻击者;如果硬币正面朝上,我们就从第二个分佈中抽样,并将样本交给攻击者。分佈如下:
(A,t=A*s + e) 其中A是用gen_mat(N,N,0,Q)产生的随机矩阵,s和e是用gen_mat(N,1,-beta,beta+1)产生的短向量。(A,t)其中A是用gen_mat(N,N,0,Q)产生的随机矩阵,t是用gen_mat(N,1,0,Q)产生的随机向量。
第一个分佈对应到我们在加密方案中实际所做的操作;在第二个中, t 只是一个随机向量,而不再是一个秘密向量。如果没有攻击者能够以明显高于一半的机率猜出抛硬币的结果,我们就说 LWE 问题是「困难的」。
如果 LWE 问题对于我们选择的参数来说很难,那麽我们的加密是被动安全的 - 这意味着密文不会洩露有关明文的任何资讯。要了解原因,请注意公钥和密文看起来都像 LWE 实例;如果我们可以用随机分佈的实例替换每个实例,那麽密文将完全独立于明文,因此不会洩露任何有关它的资讯。请注意,为了让这个论点成立,我们也必须将错误项 e3 加入密文元件 v 中。
选择参数
我们已经确定,如果解决 LWE 问题对于参数 N 、 Q 和 beta 来说都很困难,那麽破解我们的公钥加密方案也很困难。我们剩下要做的就是调整参数,以便我们能想到的任何攻击者都无法解决 LWE。这就是格发挥作用的地方。
格
格是高维空间中无限的点网格。二维格可能看起来像这样:
这些点总是遵循一个清晰的模式,类似于你在花园里看到的「格结构」:

对于密码学,我们关心一类特殊的格,它们由矩阵 P 定义,可以「辨识」格中的点。也就是说, P 所辨识的格是向量集 v ,其中 P*v == 0 ,其中「 0 」表示全零向量。在 NumPy 中,全零向量为 np.zeros((N,1), dtype=int) 。
熟悉线性代数的读者可能对格有不同的定义:一般来说,格是透过对某些基底进行线性组合而得到的点集。我们的格也可以用这种方式来表示,也就是对于辨识格的矩阵 P ,我们可以计算生成格的基底向量。然而,我们在这里并不太关心这种表现。
LWE 问题归结为区分「接近」格的一组点和「远离」格的一组点。我们分别从 LWE 实例和随机 (A,t) 建构这些点。这里我们有一个 LWE 样本(左)和一个来自随机分佈的样本(右):
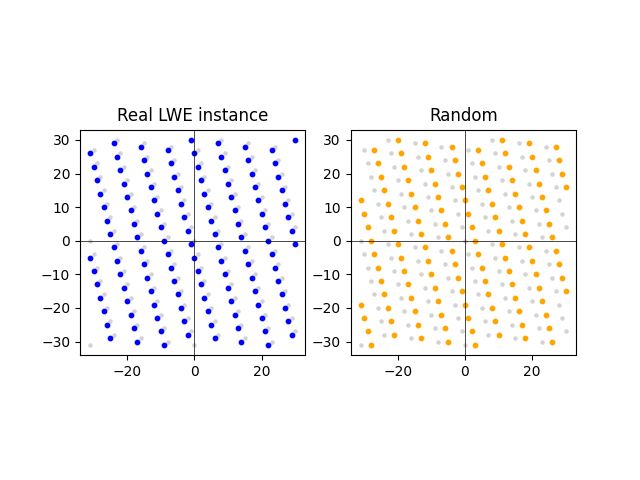
这表示 LWE 实例的点比随机实例的点更接近格。平均而言,情况确实如此。然而,虽然在二维中区分 LWE 实例和随机实例很容易,但在高维度中却变得更加困难。
让我们看看如何建立这些点。首先,让我们以 LWE 实例 (A,t=(A*s + e) % Q 为例,并考虑将 A 与单位矩阵 I 连接起来而得到的矩阵 P 来识别的格。这可能看起来像这样( N=3 ):
A = gen_mat(N, N, 0, Q)
P = np.concatenate((A, np.identity(N, dtype=int)), axis=1)
print(P)
# [[1570 634 161 1 0 0]
# [1522 1215 861 0 1 0]
# [ 344 2651 1889 0 0 1]]请注意,我们可以将 P 乘以透过连接 s 和 e ( beta=2 ) 得到的向量来计算 t :
s = gen_mat(N, 1, -beta, beta+1)
e = gen_mat(N, 1, -beta, beta+1)
t = (A*s + e) % Q
z = np.concatenate((s, e))
print(z)
# [[-2]
# [ 0]
# [-2]
# [ 0]
# [-1]
# [ 2]]
assert np.array_equal(t, P*z % Q)令 z 表示向量,并考虑点集 v ,其中 P*v == t 。根据定义,我们说这组点「接近」格,因为 z 是一个短向量。 (请记住:我们所谓的「短」是指其项以 0 和 beta 为界。)
现在考虑一个随机的 (A,t) 并考虑点集 v ,其中 P*v == t 。我们不会证明这一点,但事实是,这组点很可能「远离」格,因为不存在短向量 z 使得 P*z == t.
直观地看,随着 z 变长,解决 LWE 变得越来越难。事实上,增加 z 的平均长度(透过使 beta 更大)会增加到格的平均距离,使其看起来更像一个随机实例:
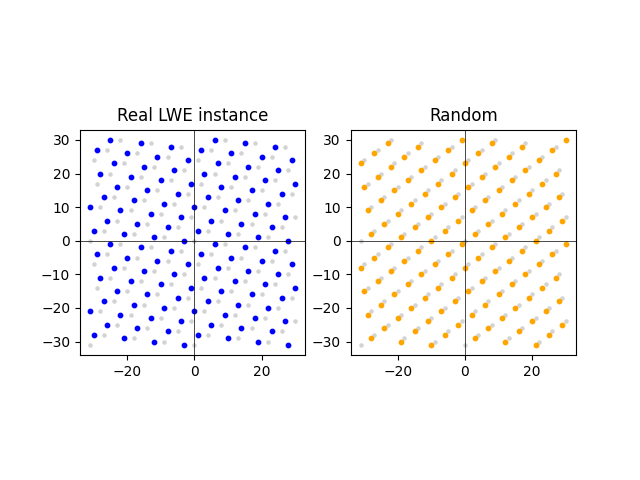
另一方面,如果 z 太长,则会产生另一个问题。
透过寻找短向量破解格密码学
给定一个随机矩阵 A ,短整数解 (SIS) 问题是找出短向量(即,其项受 beta 的限制) z1 和 z2 ,其中 (A*z1 + z2) % Q 为零。请注意,这相当于在 P 识别的格中找到一个短向量 z :
z = np.concatenate((z1, z2))
assert np.array_equal((A*z1 + z2) % Q, P*z % Q)如果我们有一个用于解决 SIS 的(量子)计算机程序,那麽我们也可以使用这个程序来解决 LWE:如果 (A,t) 是一个 LWE 实例,那麽 z1.T*t 就会很小;否则,如果 (A,t) 是随机的,则 z1.T*t 将是均匀随机的。 (你可以使用一些代数知识来说服自己这一点。)因此,为了使我们的加密方案安全,必须很难在由这些参数定义的格中找到短向量。
直观地讲,在格中找到长向量比找到短向量更容易,这意味着随着 beta 越来越接近 Q ,解决 SIS 问题变得越来越容易。另一方面,随着 beta 越来越接近 0 ,区分 LWE 实例和随机实例变得越来越容易!
这表明基于 LWE 的加密存在一种适宜性区域:如果秘密和噪音向量太短,那麽 LWE 就很容易;但如果秘密和噪音向量太长,那麽 SIS 就很容易。最佳选择是介于两者之间的某个位置。
数学够多了,给我参数吧!
为了调整我们的加密方案,我们希望选择一些参数,使得用于解决 LWE 的最有效的已知演算法(量子或经典)对于任何拥有我们能想像到的尽可能多的资源的攻击者来说都是无法触及的(如果发现新的演算法,则还需要更多的资源)。但是我们如何知道需要警惕哪些攻击呢?
幸运的是,专业格密码学家和密码分析员社群维护着一个名为格估计器的工具,它可以估计与密码学相关的格问题的最佳已知(量子)演算法的複杂性。这是我们为 ML-KEM 运行此工具时得到的结果(这需要 Sage 才能运行):
- https\://github.com/malb/lattice-estimator
sage: from estimator import *
sage: res = LWE.estimate.rough(schemes.Kyber768)
usvp :: rop: ≈2^182.2, red: ≈2^182.2, δ: 1.002902, β: 624, d: 1427, tag: usvp
dual_hybrid :: rop: ≈2^174.3, red: ≈2^174.3, guess: ≈2^162.5, β: 597, p: 4, ζ: 10, t: 60, β': 597, N: ≈2^122.7, m: 768我们最感兴趣的数字是“ rop ”,它估计了攻击将消耗的计算量。稍微使用一下这个工具,我们最终找到了一些方案参数,其中「 usvp 」和「 dual_hybrid 」攻击具有可比较的複杂性。然而,lattice-estimator 辨识出一种称为「 arora-gb 」的攻击,这种攻击适用于我们的方案,但不适用于複杂度低得多的 ML-KEM。 ( N=600 、 Q=3329 和 beta=4 ):
sage: res = LWE.estimate.rough(LWE.Parameters(n=600, q=3329, Xs=ND.Uniform(-4,4), Xe=ND.Uniform(-4,4)))
usvp :: rop: ≈2^180.2, red: ≈2^180.2, δ: 1.002926, β: 617, d: 1246, tag: usvp
dual_hybrid :: rop: ≈2^226.2, red: ≈2^225.4, guess: ≈2^224.9, β: 599, p: 3, ζ: 10, t: 0, β': 599, N: ≈2^174.8, m: 600
arora-gb :: rop: ≈2^129.4, dreg: 9, mem: ≈2^129.4, t: 4, m: ≈2^64.7我们必须进一步提高此方案的参数,使其具有与 ML-KEM 相当的安全性。
最后,需要提醒的是:在设计格密码学时,确定我们的方案是否安全需要的不仅仅是估计对我们的 LWE 参数的一般攻击的成本。由于缺乏现实对抗模型中安全性的数学证明,我们不能排除其他攻破我们方案的方法。轻轻地走,亲爱的旅行者,请带上朋友一起旅行。
提高方案效率
现在我们了解如何使用 LWE 进行加密,让我们快速了解如何使我们的方案更高效。
我们的方案的主要问题是我们一次只能加密一位。这是因为我们必须将 range(Q) 拆分成两个区块,一个区块编码 1 ,另一个区块编码 0 。我们可以透过将范围分成更多区块来提高位元率,但这会使解密错误的可能性更大。
我们的方案的另一个问题是运行时间严重依赖我们的安全参数。加密需要 次乘法(乘法是模算术安全实作中最昂贵的部分),而为了确保方案的安全,我们需要让 N 相当大。
ML-KEM 透过用多项式环上的算术代替模算术来解决这两个问题。这意味着我们的矩阵的元素将是多项式而不是整数。我们需要定义多项式的加、减、乘的含义,但是一旦我们完成了这些,加密方案的其他一切都是一样的。
事实上,你可能在小学就学过多项式算术。你可能不熟悉的唯一内容是多项式模数约简。要将两个多项式 和 相乘,我们先像往常一样将 相乘。然后我们将 除以某个特殊多项式 — — ML-KEM 使用 — — 并取馀数。我们不会尝试解释这个演算法,但重点是结果是一个具有 256 个係数的多项式,每个係数都是 range(Q) 中的整数。
使用多项式环进行算术运算的主要优点是我们可以将更多的位元打包到密文中。我们的密文公式完全相同( u=r.T*A + e2, v=r.T*t + e3 + m ),但这次明文 m 编码了一个多项式。多项式的每个係数都编码一位,我们将像以前一样处理解密错误,将 range(Q) 分成两块,一块编码 1 ,另一块编码 0 。这使我们能够可靠地加密每个密文的 256 位元(32 位元组)。
使用多项式的另一个优点是它可以显着降低矩阵的维数,而不会影响安全性。具体来说,ML-KEM 最广泛使用的变体 ML-KEM-768 使用 3 × 3 矩阵 A ,因此总共只有 9 个多项式。 (请注意256*3=768 ,因此得名“ML-KEM-768”。)但是,请注意,我们必须小心选择模数: 很特殊,因为它没有表现出任何已知允许攻击的代数结构。
係数模数选择 Q=3329 、多项式模数选择 还有一个好处。允许使用 NTT 演算法进行多项式乘法,从而大大减少了我们必须执行的乘法和加法的次数。事实上,这种最佳化是 ML-KEM 在 CPU 时间方面有时比使用椭圆曲线的密钥交换更快的主要原因。
我们不会在这里讨论 NTT 的工作原理,只是说如果你曾经实现过 RSA,那麽演算法对你来说会看起来很熟悉。在这两种情况下,我们都使用中国剩馀定理将乘法分解为多个更便宜、模数更小的乘法。
从公钥加密到 ML-KEM
建构 ML-KEM 的最后一步是确保该方案能够抵禦**选择密文攻击 (CCA)**。目前,它仅对选择明文攻击(CPA)是安全的,这基本上意味着无论明文如何分佈,密文都不会洩露有关明文的资讯。 CCA 安全性更强,因为它允许攻击者存取其选择的密文的解密。 (当然,不允许解密目标密文本身。)ML-KEM 中使用的特定变换产生了 CCA 安全的 KEM(「密钥封装机制」)。
选择密文攻击可能看起来有点抽象,但实际上它们为 KEM(以及公钥加密)的许多应用形式形式化了一个现实的威胁模型。例如,假设我们在协议中使用该方案,其中伺服器透过证明其能够解密客户端产生的密文来向客户端验证其身分。在这种协议中,伺服器充当一种“解密预言机”,其对客户端的回应取决于密钥。除非该方案是 CCA 安全的,否则攻击者可能会滥用此预言机,随着时间的推移洩露有关密钥的信息,最终使其能够冒充伺服器。
ML-KEM 融入了更多优化,使其尽可能快速且紧凑。例如,我们不是产生随机矩阵 A ,而是可以使用基于杂凑的原语(称为 XOF(「可扩展输出函数」),从一个随机的 32 个位元组字串(称为「种子」)中派生出它,在 ML-KEM 的情况下,这个 XOF 是 SHAKE128。这大大减少了公钥的大小。
另一个有趣的最佳化是,透过对每个係数的最低有效位元进行四捨五入来压缩密文中的多项式係数( range(Q) 中的整数),从而减少密文的整体大小。
总而言之,对于最广泛部署的参数(ML-KEM-768),公钥为 1184 位元组,密文为 1088 位元组。除了减少封装密钥的大小或公共矩阵 A 的大小之外,没有明显的方法可以减少这种情况。前者会使 ML-KEM 适用于较少的应用程序,而后者会降低安全边际。
还有其他较小的格方案,但它们基于不同的困难假设且仍在进行分析。
- https\://eprint.iacr.org/2022/031
认证
在上一节中,我们了解了 ML-KEM,该演算法已用于实现 PQ 安全的加密。然而,加密只是难题的一个面向:建立安全连线还需要对伺服器进行认证——有时还需要对客户端进行认证,具体取决于应用程式。
认证通常由数位签名方案提供,该方案使用密钥对讯息进行签名,并使用公钥来验证签名。目前使用的签名方案不是 PQ 安全的:可以使用量子电脑计算与伺服器公钥相对应的密钥,然后使用该密钥冒充伺服器。
虽然这种威胁不如加密威胁那麽紧迫,但缓解这种威胁将会更加複杂。多年来,我们在 TLS 握手中加入了许多签名,以满足 Web PKI 不断变化的需求。我们有这些签名的 PQ 替代方案,其中一种我们将在本节中进行研究,但到目前为止,这些签名及其公钥太大(即佔用太多位元组),无法轻松取代当今的方案。除非 NIST 正在进行的标准化工作取得突破,否则我们将不得不重新设计 TLS 和 Web PKI 以使用更少的签名。
- https\://blog.cloudflare.com/another-look-at-pq-signatures/
现在,让我们深入研究我们可能首先看到的部署的 PQ 签名方案:ML-DSA,又称为 Dillithium。 ML-DSA 的设计遵循与 ML-KEM 类似的模板。我们首先建构一些中间原语,然后将该原语转换为我们想要的原语,在本例中为签名方案。
- https\://csrc.nist.gov/pubs/fips/204/final ML-DSA 比 ML-KEM 複杂得多,因此我们将尝试进一步简化它并尝试传达其主要思想。
预热
ML-KEM 基本上是用格代替椭圆曲线的 El Gamal 加密,而 ML-DSA 基本上是用格代替椭圆曲线的 Schnorr 身分识别协议。证明者使用 Schnorr 协议来说服验证者,使其知道与其公钥相关联的密钥,而无需洩露密钥本身。该协议有三个步骤,并使用四种演算法执行:
- https\://www.zkdocs.com/docs/zkdocs/zero-knowledge-protocols/schnorr/
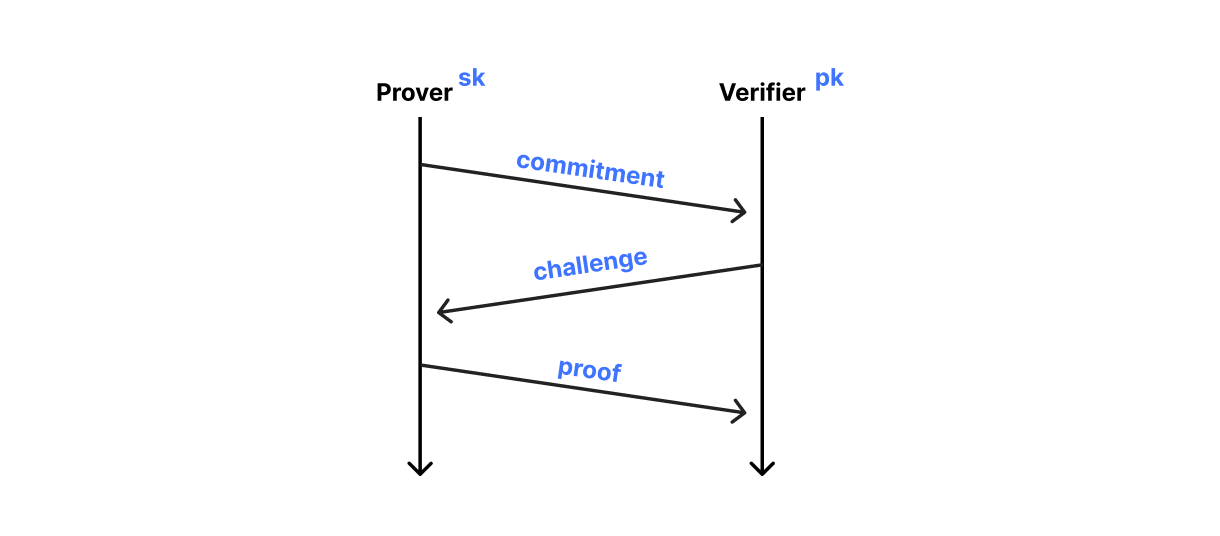
initialize():证明者初始化协议并向验证者发送承诺challenge():验证者收到承诺并向证明者发送挑战finish():证明者接收挑战并向验证者发送证明verify():最后,验证者使用证明来判断证明者是否知道密钥
透过使该协议非互动式,我们就得到了 ML-DSA 的高级结构。具体来说,证明者透过将承诺与要签署的讯息一起进行杂凑来得出挑战本身。签名由承诺和证明组成:为了验证签名,验证者根据承诺和讯息重新计算挑战,并照常执行 verify() 。
让我们直接开始从格建造 Schnorr 的识别协议。如果你以前从未见过该协议,那麽它乍一看会有点像黑魔法。我们将慢慢地进行研究,以了解其工作原理和原因。
与 ML-KEM 一样,我们的公钥是一个 LWE 实例 (A,t=A*s1 + s2) 。不过,这次我们的密钥是一对短向量 (s1,s2) ,也就是它包含了误差项。除此,密钥产生完全相同:
def key_gen():
A = gen_mat(N, N, 0, Q)
s1 = gen_mat(N, 1, -beta, beta+1)
s2 = gen_mat(N, 1, -beta, beta+1)
t = (A*s1 + s2) % Q
return ((A, t), (s1, s2))为了初始化协议,证明者产生另一个 LWE 实例 (A,w=A*y1 + y2) 。你马上就会明白为什麽。证明者发送 w 的杂凑值作为其承诺:
def initialize(A):
y1 = gen_mat(N, 1, -beta, beta+1)
y2 = gen_mat(N, 1, -beta, beta+1)
w = (A*y1 + y2) % Q
return (H(w), (y1, y2))这里 H 是一些加密杂凑函数,例如 SHA-3。证明者储存秘密向量 (y1,y2) 以供下一步使用。
现在到了验证者挑战的时间了。挑战只是一个整数,但我们需要谨慎选择它。现在让我们随机挑选一下:
def challenge():
return random.randrange(0, Q)请记住:当我们将此协议转换为数位签名时,挑战源自于承诺、 H(w) 和讯息。此杂凑函数的范围必须与 challenge() 的输出集相同。
现在到了有趣的部分。证明是一对满足 A*z1 + z2 == c*t + w 的向量 (z1,z2) 。如果我们知道密钥,我们可以轻松地提供这个证明:
z1 = (c*s1 + y1) % Q
z2 = (c*s2 + y2) % Q
则 A*z1 + z2 == A*(c*s1 + y1) + (c*s2 + y2) == c*(A*s1 + s2) + (A*y1 + y2) == c*t + w 。我们的目标是设计这样的协议:即使在观察了该协议的多次执行之后,也很难在不知道 (s1,s2) 的情况下提出 (z1,z2) 。
以下是完整的 finish() 和 verify() 演算法:
def finish(s1, s2, y1, y2, c):
z1 = (c*s1 + y1) % Q
z2 = (c*s2 + y2) % Q
return (z1, z2)
def verify(A, t, hw, c, z1, z2):
return H((A*z1 + z2 - c*t) % Q) == hw
# 测试
((A, t), (s1, s2)) = key_gen()
(hw, (y1, y2)) = initialize(A) # hw: prover -> verifier
c = challenge() # c: verifier -> prover
(z1, z2) = finish(s1, s2, y1, y2, c) # (z1, z2): prover -> verifier
assert verify(A, t, hw, c, z1, z2) # verifier请注意,验证程式实际上并不会直接检查 A*z1 + z2 == c*t + w ;我们必须重新排列等式,以便将承诺设为 H(w) 而不是 w 。我们将在下一节解释杂凑的必要性。
让这个方案安全
该协议是否安全的问题归结为是否有可能在不知道密钥的情况下冒充证明者。让我们戴上攻击者的帽子,四处探索。
也许有一种方法可以计算出密钥,要么直接从公钥计算,要么透过窃听诚实证明者对协议的执行。如果 LWE 很难,那麽显然我们无法从公钥 t 中提取私钥。同样,承诺 H(w) 不会洩露任何有助于我们从证明 (z1,z2) 中提取密钥的资讯。
让我们仔细看看证据。请注意,向量 (y1,y2) 「掩盖」了密钥向量,就像 ML-KEM 中的共享密钥掩盖了明文一样。然而,有一个很大的例外:我们也透过挑战 c 来缩放密钥向量。
缩放这些向量会产生什麽效果?如果我们仔细观察一些证据,我们就会开始看到一种模式出现。我们先来看看 z1 ( N=3, Q=3329, beta=4 ):
((A, t), (s1, s2)) = key_gen()
print('s1={}'.format(s1.T % Q))
for _ in range(10):
(w, (y1, y2)) = initialize(A)
c = challenge()
(z1, z2) = finish(s1, s2, y1, y2, c)
print('c={}, z1={}'.format(c, z1.T))
# s1=[[ 1 0 3326]]
# c=1123, z1=[[1121 3327 3287]]
# c=1064, z1=[[1060 4 137]]
# c=1885, z1=[[1884 3327 999]]
# c=269, z1=[[ 270 3325 2524]]
# c=1506, z1=[[1510 3325 2141]]
# c=3147, z1=[[3149 4 547]]
# c=703, z1=[[ 700 4 1219]]
# c=1518, z1=[[1518 3327 2104]]
# c=1726, z1=[[1726 0 1478]]
# c=2591, z1=[[2589 4 2217]]事实上,有了足够的证明样本,我们应该能够对 s1 的值做出相当好的猜测。事实上,对于这些参数,我们可以进行一个简单的统计分析来准确计算 s1 。 (提示: Q 是质数,这表示每当 c>0 时就有 c*pow(c,-1,Q)==1 。)我们也可以将此分析应用于 s2 ,或直接从 t 、 s1 和 A 计算出来。
我们的协议的主要缺陷是,儘管我们的秘密向量很短,但缩放它们会使它们变得太长,以至于不能完全被 (y1,y2) 掩盖。由于 c 跨越整个 range(Q) ,因此 c*s1. 和 c*s2, 的项也跨越整个 range(Q) ,这意味着为了屏蔽这些项,我们需要 (y1,y2) 的项也跨越 range(Q) 。然而,透过解决 SIS,这样做可以使解决 (A,w) 的 LWE 变得容易。我们需要在 LWE 实例的向量长度和挑战造成的洩漏之间取得平衡。
这就是事情变得棘手的地方。我们将 challenge() 的可能输出集合称为挑战空间。我们需要挑战空间够大,大到两次输出相同挑战的机率可以忽略不计。
为什麽这样的碰撞会成为一个问题?在数位签名的背景下,这更容易看出来。假设攻击者知道讯息 m 的有效签名。签名包含承诺 H(m) ,因此攻击者也知道挑战是 c == H(H(w),m) 。假设它设法找到不同的讯息 m * ,其中 c == H(H(w),m * ) 。那麽该签名对于 m 来说也是有效的!如果挑战空间(即 H 的可能输出集)太小,这种攻击很容易发生。
不幸的是,我们不能仅仅透过增加模数 Q 的大小来扩大挑战空间:挑战越大,我们洩漏的有关密钥的资讯就越多。我们需要一个新的想法。
两全其美
请记住,LWE 的难度取决于 beta 和 Q 之间的比率。这意味着 y1 和 y2 不需要绝对短,但相对于随机向量来说要短。
考虑到这一点,请考虑以下想法。让我们取一个更大的模数,例如 Q=2**31 - 1 ,我们将继续从相同的挑战空间 range(2**16) 中取样。
首先,请注意 z1 现在「相对」较短,因为它的项现在位于 range(-gamma, gamma+1) 中,其中 gamma = beta*(2**16-1), 而不是均匀分佈在 range(Q) 上。我们也修改 initialize() 以从同一范围中对 (y1,y2) 的项进行取样,看看会发生什麽:
def initialize(A):
y1 = gen_mat(N, 1, -gamma, gamma+1)
y2 = gen_mat(N, 1, -gamma, gamma+1)
w = (A*y1 + y2) % Q
return (H(w), (y1, y2))
((A, t), (s1, s2)) = key_gen()
print('s1={}'.format(s1.T % Q))
for _ in range(10):
(w, (y1, y2)) = initialize(A)
c = challenge()
(z1, z2) = finish(s1, s2, y1, y2, c)
print('c={}, z1={}'.format(c, z1.T))
# s1=[[3 0 1]]
# c=31476, z1=[[175933 141954 93186]]
# c=27360, z1=[[ 136404 2147438807 283758]]
# c=33536, z1=[[2147430945 2147377022 190671]]
# c=23283, z1=[[186516 73400 4955]]
# c=24756, z1=[[ 328377 2147438906 2147388768]]
# c=12428, z1=[[2147340715 188675 90282]]
# c=24266, z1=[[ 175498 2147261581 2147301553]]
# c=45331, z1=[[357595 185269 177155]]
# c=45641, z1=[[ 21592 2147249191 2147446200]]
# c=57893, z1=[[297750 113335 144894]]这肯定是朝着正确的方向发展的,因为 z1 和 s1 之间没有明显的相关性。 ( z2 和 s2 也是如此。)然而,我们还没有到达那里。
一个问题是挑战空间仍然相当小。由于只有 2**16 个挑战可供选择,即使只执行了几次协议,我们也可能会看到冲突。我们需要的挑战空间大得多,比如说在 2**256 左右。但为了确保 beta 和 Q 之间的比例安全, Q 必须是一个非常大的数字。
由于 ML-DSA 使用多项式环上的算术,因此能够避开这个问题。它使用与 ML-KEM 相同的模多项式,因此挑战是具有 256 个係数的多项式。係数经过精心选择,使得挑战空间很大,但乘以挑战会使秘密向量小幅变化。请注意,我们最终对 ML-DSA 使用的模量( Q=8380417 )仍然比 ML-KEM 稍大,但仅大约 12 位元。
然而,这里有一个更根本的问题,那就是我们还没有完全排除签名可能洩露有关密钥的资讯。
因和果
假设我们运行该协议多次,并且在每次运行中,我们碰巧为 y1 的某些项选择一个相对较小的值。经过足够多次运行后,我们最终可以重建 s1 的相应项。为了排除这个可能性,我们需要让 y1 变得更长。 (对于 y2 也同样如此。)但是要多久呢?
假设我们知道对于某些 beta_loose > beta , z1 和 z2 的项总是在 range(-beta_loose,beta_loose+1) 中。然后我们可以模拟协议的诚实运行,如下所示:
def simulate(A, t):
z1 = gen_mat(N, 1, -beta_loose, beta_loose+1)
z2 = gen_mat(N, 1, -beta_loose, beta_loose+1)
c = challenge()
w = (A*z1 + z2 - c*t) % Q
return (H(w), c, (z1, z2))
# 测试
((A, t), (s1, s2)) = key_gen()
(hw, c, (z1, z2)) = simulate(A, t)
assert verify(A, t, hw, c, z1, z2)这个过程完美地模拟了协议的诚实运行,因为 simulate() 的输出与诚实证明者实际运行的协议的记录没有区别。为了理解这一点,请注意 w 、 c 、 z1 和 z2 都具有相同的数学关係(验证方程式仍然成立)并且具有相同的分佈。
这就是关键所在:由于这个过程不使用密钥,因此攻击者透过窃听诚实的证明者却无法获得任何讯息,因为诚实的证明者无法透过公钥本身计算出任何资讯。非常漂亮!
剩下要做的就是安排 z1 和 z2 落入该范围内。首先,我们将 y1 和 y2 的范围增加 beta_loose 来修改 initialize() :
def initialize(A):
y1 = gen_mat(N, 1, -gamma+beta_loose, gamma+beta_loose+1)
y2 = gen_mat(N, 1, -gamma+beta_loose, gamma+beta_loose+1)
w = (A*y1 + y2) % Q
return (H(w), (y1, y2))这确保了证明向量 z1 和 z2 在 range(-beta_loose, beta_loose+1) 上大致均匀。然而,它们可能稍微超出这个范围,所以如果不是,则需要修改 finalize() 以中止。相应地, verify() 应该拒绝超出范围的证明向量:
def finish(s1, s2, y1, y2, c):
z1 = (c*s1 + y1) % Q
z2 = (c*s2 + y2) % Q
ifnot in_range(z1, beta_loose) ornot in_range(z2, beta_loose):
return (None, None)
return (z1, z2)
def verify(A, t, hw, c, z1, z2):
ifnot in_range(z1, beta_loose) ornot in_range(z2, beta_loose):
returnFalse
return H((A*z1 + z2 - c*t) % Q) == hw如果 finish() 传回 (None,None) ,则证明者和验证者应中止协议并重试,直到协议成功:
((A, t), (s1, s2)) = key_gen()
while True:
(hw, (y1, y2)) = initialize(A) # hw: prover -> verifier
c = challenge() # c: verifier -> prover
(z1, z2) = finish(s1, s2, y1, y2, c) # (z1, z2): prover -> verifier
if z1 is not None and z2 is not None:
break
assert verify(A, t, hw, c, z1, z2)有趣的是,我们预计中止将会相当常见。 ML-DSA 的参数经过调整,使得协议平均运行五次才能成功。
另一个有趣的点是,安全性证明要求我们不仅模拟成功的协议运行,还模拟中止的协议运行。更具体地说,协议模拟器必须以与真实协议相同的机率中止,这意味着拒绝机率与密钥独立。
模拟器还需要能够为中止的脚本产生看起来逼真的承诺。这正是证明者承诺 w 的杂凑值而不是 w 本身的原因:在安全证明中,我们可以轻松模拟随机输入的杂凑值。
提高方案效率
ML-DSA 受益于与 ML-KEM 相同的许多最佳化,包括使用多项式环、NTT 进行多项式乘法以及使用固定位数对多项式进行编码。然而,ML-DSA 还有一些技巧可以变得更小。
首先,在 ML-DSA 中,证明不是由一对短向量 z1 和 z2 组成,而是由单一向量 z=c*s1 + y, 组成,其中 y 是在上一个步骤中提交的。反过来,我们最终只得到一个证明向量 z ,而不是像以前那样得到两个。要使其发挥作用,需要对承诺进行特殊编码,以便我们无法从中计算出 y 。 ML-DSA 使用相关技巧来减少公钥的 t 向量的大小,但细节更为複杂。
对于我们预计首先部署的参数(ML-DSA-44),公钥长度为 1312 字节,签名则长达 2420 位元组。与 ML-KEM 相比,可以减少更多位元组。这并不是免费的,需要让方案複杂化。一个例子是 HAETAE,它改变了所使用的分佈。 Falcon 更进一步,採用了更小的签名,採用了完全不同的方法,虽然很优雅,但实现起来也更複杂。
- https\://eprint.iacr.org/2023/624.pdf
- https\://github.com/pornin/rust-fn-dsa
总结
格密码学是第一代在网路上广泛部署的 PQ 演算法的基础。 ML-KEM 目前已被广泛用于保护量子电脑的加密,并且在未来几年中,我们期望看到 ML-DSA 得到部署,以应对量子电脑对认证的威胁。
格也是密码学新领域的基础:对加密资料进行计算。
假设你想要总结客户提交的一些指标,而不想了解这些指标本身。使用基于 LWE 的加密,你可以安排每个用户端在提交之前加密其指标,聚合密文,然后解密以获得聚合。
- https\://eprint.iacr.org/2024/936
假设伺服器有一个资料库,它希望向客户端提供对该资料库的存取权限,但又不向伺服器透露客户端想要查询资料库的哪些行。基于 LWE 的加密允许以加密查询的方式对资料库进行编码。
- https\://eprint.iacr.org/2022/949
这些应用是称为 FHE(「全同态加密」) 的范例的特殊情况,它允许对加密资料进行任意计算。 FHE 是一种极其强大的原语,而我们今天所知的建造它的唯一方法是使用格。然而,对于大多数应用而言,FHE 的实用性远不如专用协议(无论是否基于格)。儘管如此,多年来我们已经看到 FHE 变得越来越好,对于许多应用来说它已经是一个不错的选择。也许我们会在未来的部落格文章中深入探讨这个和其他格方案。
我们希望你喜欢这次旋风式的格之旅。感谢阅读!
<!--EndFragment-->
- 各后量子密码学算法安全性评估 1206 浏览
- 通过 ℓ₂-范数检查实现更高效的格折叠 1387 浏览
- 666 - PQC 野兽的密文大小? 782 浏览
- 格密码学基础(五)(完结篇):基于Σ-协议构造数字签名 805 浏览
- 基于格的哈希函数 1546 浏览
- QIP: 2 适用于格密码的确定性分层钱包方案 1266 浏览
- Labrador:后量子 ZK 证明的新纪元 1479 浏览
- 全同态加密与真正隐私互联网的曙光 2698 浏览
- 通过ℓ₂-范数检查实现更高效的格折叠 838 浏览
- 我们来了解一下拉布拉多协议 1357 浏览
- 准备好迎接FN-DSA:比Dilithium慢,但密钥/密文更小 2465 浏览

