a/(b+c) + b/(c+a) + c/(a+b) = 4 的一个简单解释

a/(b+c) + b/(c+a) + c/(a+b) = 4 的简单解释

a/(b+c) + b/(c+a) + c/(a+b) = 4 的简单解释

你可能在某个时候看过这个数学难题：

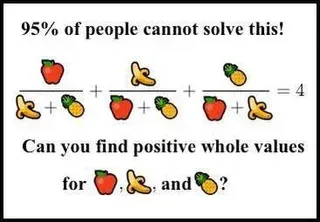
这个难题在互联网上获得了一定的知名度，因为它看起来要么很简单，要么不可能，要么是个脑筋急转弯（解决 P = NP？哈哈哈，答案是 N = 1，捉到你了吧！），但实际上这三者都不是。这个问题完全就是它看起来的样子。这个问题是可以解决的。然而，最小的解是：

a = 154476802108746166441951315019919837485664325669565431700026634898253202035277999
b = 36875131794129999827197811565225474825492979968971970996283137471637224634055579
c = 4373612677928697257861252602371390152816537558161613618621437993378423467772036

这到底是怎么回事？？！如果你在互联网上搜索，你会看到关于这个问题实际上是如何与 椭圆曲线 联系起来的，以及来自你从未听说过的代数几何的其他花哨术语的冗长解释，即使你认为自己对椭圆曲线无所不知，因为你是个 密码学家 加密爱好者。

这篇文章的目标是尽可能地以最基本的方式解释这个难题，而不依赖于对这些概念的任何先有知识。

首先，让我们从一个宽松的问题版本开始。具体来说，让我们删除这三个值必须为正的要求。事实证明，你可以尝试一堆可能性，并通过纯粹的人工暴力破解得到两个答案：（−11,−4,1) 和 (11,−5,9)。你可以通过重新排列数字、翻转符号和乘以常数因子从这两个答案中获得更多解（例如，(−2,8,22) 也是一个有效的解），但我们将把这些视为相同的解。

现在，我们进入有趣的部分。如果我们能想出一种组合两个解并得到一个全新的第三个解的方法呢？通常，这在数学中是可能的：如果你有两个 5 的倍数，那么它们的和也是 5 的倍数。更重要的是，如果你在一个圆上有两个有理点（即，(p1q1,r2s2) 和 (p2q2,r2s2) 满足 (piqi)2+(risi)2=1)，你可以使用点加法法则在圆上生成第三个有理点：(p1p2q1q2−r1r2s1s2,p1r2q1s2−r1p2s1q2)。

如果我们能为我们的问题提出这样一个算法，那么我们就可以一遍又一遍地使用它，直到最终我们通过纯粹的运气得到一个碰巧全部为正的点。这将是我们的解决方案路径。

让我们通过使其成为二维问题来简化问题。请注意，该方程式是齐次的：它具有将所有输入按相同数字缩放不会改变答案的属性。让我们用它来删除 c 变量：

ab+1+ba+1+1a+b−4=0

我们还将 4 移到了左边，这将使我们稍后更加方便。对于任何具有有理 a=pq 和 b=rs 的解，都对应于原始方程式的整数解：(a∗qs,b∗qs,qs)。

现在，让我们乘以分母，使整个方程式成为一个纯粹的多项式：

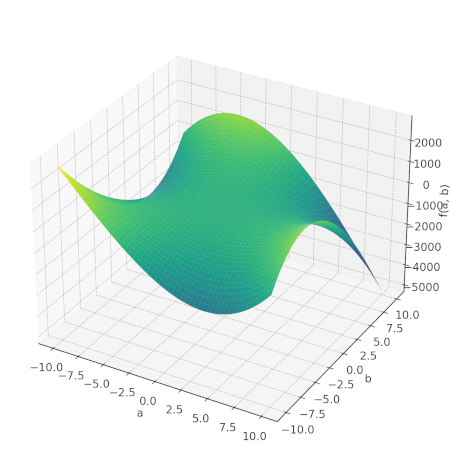
a(a+1)(a+b)+b(b+1)(a+b)+(a+1)(b+1)−4(a+1)(b+1)(a+b)=0

这引入了一些无关的解，例如 (a=1,b=−1)。但我们只是忽略它们。我们可以将上面的表达式绘制成函数；它看起来像这样：

现在，让我们画一条穿过我们知道这条曲线与 z=0 平面相交的两个点的线：（−11,−4) 和 (119,−59)。我们通过从三值方程式的两个解开始，并将 (a,b,c)→(ac,bc) 进行转换来推导出这些解。

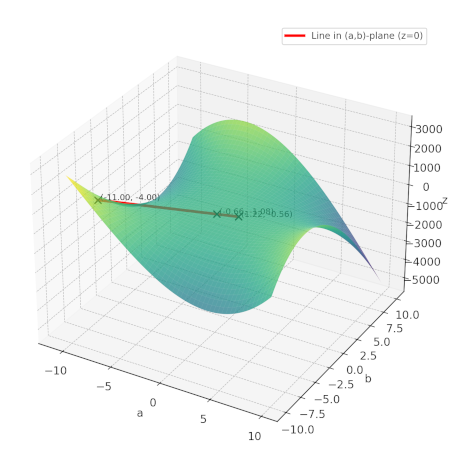
正如我们所看到的，这条线有第三个交点。并且因为这条线沿着 z=0 平面，所以第三个点也必须沿着 z=0 平面，因此它也必须是一个解。现在，让我们证明这个点是有理的，所以它仍然对应于原始问题的有效解。

我们可以将这条线参数化为 (a=−11+(119+11)∗t,b=−4+(−59+4)∗t)。t=0 给出第一个点，t=1 给出第二个点。然后，我们可以通过用基于 t 的表达式替换 a 和 b 来查看 a(a+1)(a+b)+b(b+1)(a+b)+(a+1)(b+1)−4(a+1)(b+1)(a+b) 沿着这条线 的表现。

这给了我们曲线：y=907181∗t3+1674881∗t2+767781∗t。这是该曲线的图，显示了所有三个交点：

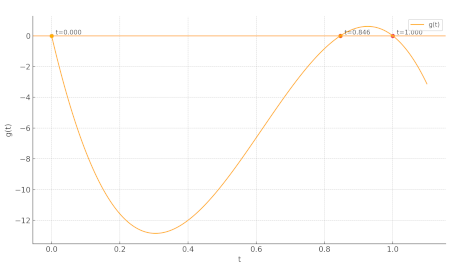
然后，你可以获取新的 t 并将其插入到该行中，并得到你的新点：(−59519071,−98419071)。

新 t（以及因此的新点）是有理数的根本原因是：曲线是 t 中的一个 3 次多项式，如果一个 3 次多项式有三个解，那么它可以完全分解为 k(x−a)(x−b)(x−c)。它的 2 次项等于 −k(a+b+c)。因此，如果 2 次项和 3 次项是有理数（它们是有理数，因为我们通过一个具有有理系数的方程式构造了该多项式），并且其中两个解是有理数，则第三个解也必须是有理数。

从这里，我们可以强行得到更多的解。不幸的是，我们不能直接使用我们拥有的三个点继续前进：如果你要重复上述过程以从我们现在拥有的三个点中的任意两个点开始生成一个新点，你只会得到第三个点。为了解决这个问题，我们将使用一个巧妙的技巧来生成更多的解：将 (x,y) 转换为 (y,x)。

现在，考虑到这一点，我们只需暴力破解，反复使用“找到线上第三个点”算法和坐标翻转来获得尽可能多的新解。这是 python 代码：

from sympy import symbols, Poly, solve, simplify, Rational, expand
from math import lcm

def find_third_point(a1, b1, a2, b2):
    """
    找到三次曲线 a(a+1)(a+b) + b(b+1)(a+b) + (a+1)(b+1) = 4(a+1)(b+1)(a+b) 上通过点 (a1, b1) 和 (a2, b2) 的线的第三个交点。

    Args:
        a1, b1: 第一个点的坐标（有理数）
        a2, b2: 第二个点的坐标（有理数）

    Returns:
        Tuple (a3, b3): 第三个交点的坐标
    """
    # 定义符号变量
    t, a, b = symbols('t a b')

    # 参数化直线：a = a1 + t*(a2 - a1), b = b1 + t*(b2 - b1)
    a_expr = a1 + t * (a2 - a1)
    b_expr = b1 + t * (b2 - b1)

    # 定义三次曲线方程：
    # a(a+1)(a+b) + b(b+1)(a+b) + (a+1)(b+1) = 4(a+1)(b+1)(a+b)
    left_side = a * (a + 1) * (a + b) + b * (b + 1) * (a + b) + (a + 1) * (b + 1)
    right_side = 4 * (a + 1) * (b + 1) * (a + b)
    equation = left_side - right_side

    # 将直线参数化代入方程
    poly_t = equation.subs({a: a_expr, b: b_expr})

    # 简化并转换为 t 中的多项式
    poly_t = expand(poly_t)
    poly = Poly(poly_t, t)

    # 获取三次多项式的系数
    coeffs = poly.coeffs()

    # 多项式是三次的（3 次），所以 coeffs = [c3, c2, c1, c0]
    # 对于三次多项式 c3*t3 + c2*t2 + c1*t + c0，根的和为 -c2/c3
    while len(coeffs) < 4:
        coeffs.append(0)
    if len(coeffs) != 4:
        raise ValueError("Unexpected polynomial degree. Expected cubic polynomial.")

    c3, c2, c1, c0 = coeffs

    # 已知的根是 t=0（对于点 1）和 t=1（对于点 2）
    # 根的和：t1 + t2 + t3 = -c2/c3
    # 因为 t1 = 0, t2 = 1, 我们有 0 + 1 + t3 = -c2/c3
    t3 = -c2 / c3 - (0 + 1)

    # 计算第三个点的坐标
    a3 = a1 + t3 * (a2 - a1)
    b3 = b1 + t3 * (b2 - b1)

    # 简化结果以确保有理数输出
    a3 = simplify(a3)
    b3 = simplify(b3)

    return (a3, b3)

# 验证点是否在曲线上
def is_on_curve(a, b):
    left = a * (a + 1) * (a + b) + b * (b + 1) * (a + b) + (a + 1) * (b + 1)
    right = 4 * (a + 1) * (b + 1) * (a + b)
    return left == right

def is_too_big(x, y):
    xn, xd = x.as_numer_denom()
    yn, yd = y.as_numer_denom()
    return max(abs(xn), abs(xd), abs(yn), abs(yd)) > 10**200

def find_smallest_all_positive_point():
    points = [(Rational(-11, 1), Rational(-4, 1)), (Rational(11, 9), Rational(-5, 9))]
    queue = [(points[0], points[1])]

    def accept(x, y):
        print(x, y)
        for (x2, y2) in points:
            queue.append(((x2, y2), (x,y)))
        points.append((x, y))

    while len(queue) > 0:
        print(len(queue))
        (x1, y1), (x2, y2) = queue.pop()
        x3, y3 = find_third_point(x1, y1, x2, y2)
        if not is_too_big(x3, y3):
            if (x3, y3) not in points:
                accept(x3, y3)
            if (y3, x3) not in points:
                accept(y3, x3)

    print(points)
    eligible = [(x,y) for (x,y) in points if x > 0 and y > 0]
    return min(
        eligible,
        key=lambda x: lcm(x[0].as_numer_denom()[1], x[1].as_numer_denom()[1])
    )

这非常低效，但它完成了工作。我们得到：

(154476802108746166441951315019919837485664325669565431700026634898253202035277999/4373612677928697257861252602371390152816537558161613618621437993378423467772036, 36875131794129999827197811565225474825492979968971970996283137471637224634055579/4373612677928697257861252602371390152816537558161613618621437993378423467772036)

这是二元方程式的一个正有理解；加上 c=1，你就得到了三元方程式的一个正有理解。从这里，我们乘以分母，得到原始解：

a = 154476802108746166441951315019919837485664325669565431700026634898253202035277999
b = 36875131794129999827197811565225474825492979968971970996283137471637224634055579
c = 4373612677928697257861252602371390152816537558161613618621437993378423467772036

这并不能证明这是最小的解：为此，你实际上必须深入研究我试图避免的更深奥的椭圆曲线理论。但它为你提供了一个问题的解，并且底层的数学实际上是伪装的椭圆曲线数学：“找到线上第三个相交点并翻转坐标” 与 椭圆曲线加法法则 完全相同，只是沿着对角轴而不是 x 轴翻转。我们提出的这种“加法法则” 甚至满足结合律。

• 原文链接： vitalik.eth.limo/general...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～