椭圆曲线深度剖析（第六部分）

上次我们学习了约数的语言。这对于更深入地理解椭圆曲线至关重要，并且对于理解 配对 也是至关重要的——我们将在接下来的几篇文章中讨论这个构造。

不过在此之前，我想花时间真正地沉浸于理论之中，并探索一些我们在分析过程中通常认为理所当然的事情，但实际上这些事情 一点也不明显。

我保证——这将是（至少在接触配对之前）最后一波奇怪的理论知识了！

话虽如此，本文可能不如其他文章那么实用，而更多地侧重于纯理论。尽管如此，计数 椭圆曲线中的 点 的能力仍然非常重要，但我们今天不会质疑为什么。

事不宜迟，我们开始吧！

有理点(Rational Points)

在有限域上使用椭圆曲线时，一个基本假设是曲线上存在具有 整数坐标 的点。

比如 (1,1)、(2,3) 或 (5,8) 这样的点。

稍微思考一下。这看起来显而易见吗？我们总能找到这些 整数值 的点吗？

更一般地说，我们可以尝试找到 有理点：坐标是有理数的点。根据曲线的不同，确定曲线是否具有有理点可能非常容易，也可能 极其复杂。

事实上，寻找曲线上的有理点是 丢番图方程 的一个经典例子——丢番图方程是指目标是寻找整数或有理解的多项式方程。

费马最后定理（Fermat’s Last Theorem）花费了 350 多年的时间才被证明，也许是最著名的例子。

猜猜椭圆曲线属于这两类中的哪一类...

是的，当然 是后者。

为什么？？？

为了很好地理解寻找有理点背后的思路，我们首先关注一条熟悉的曲线，在这条曲线上找到有理点非常容易：一个圆。

圆上的有理点

圆由这个简单的等式表示：

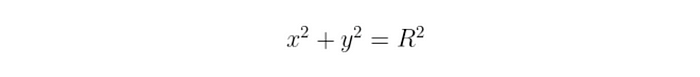
其中 R 是半径。我们该如何找到这条曲线上的有理点呢？

让我们首先尝试找到至少 一个。碰巧的是，圆与坐标轴的所有交点都是有理点：(1,0)、(0,1)、(-1,0) 和 (0,-1)。

好的开始！现在，我们将这些点用作 种子。以点 (0,1) 为例。然后，画一条穿过它的直线，这条直线具有有理斜率 m，我们可以将其写成 m₁ / m₂。如果计算出得到的直线方程，你将得到：

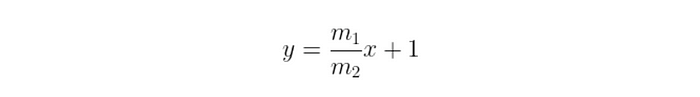
这条线将与圆相交于 另一点：

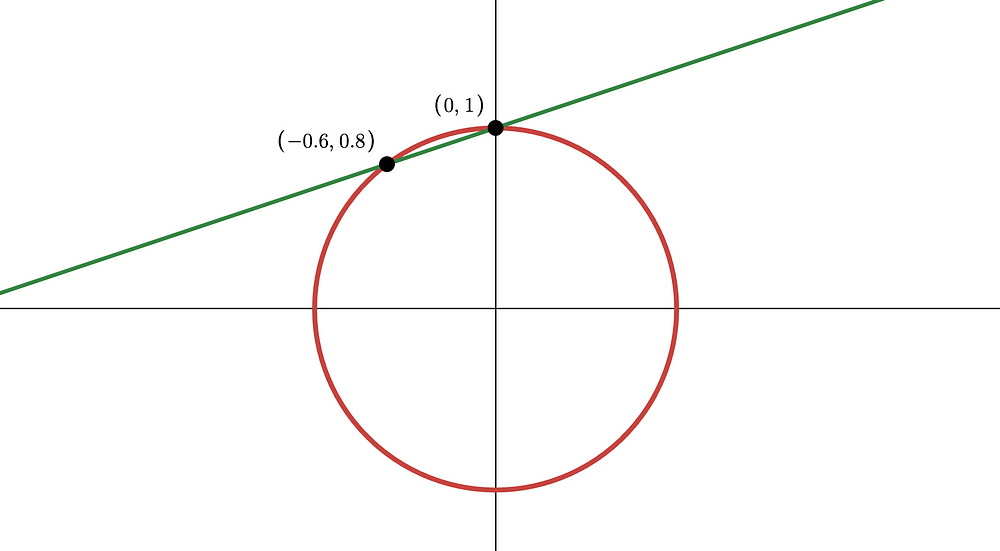
我这里使用的斜率是 1/3。你可以在 Desmos 中自己尝试一下。

哦，这是什么？新的点是 有理的！

这只是侥幸吗？

不，并非如此。然而，证明这一点需要做一些工作。

Galois 共轭(Conjugates)

我们首先需要定义什么是 有理函数：它是一个可以表示为具有 有理系数 的两个 多项式 的比率的函数。我们的直线显然是一个有理函数——毕竟，它本身就是一个具有有理系数的多项式！

当我们使用这些有理函数时，曲线和我们的有理函数之间的交点满足一个特殊的条件。

只有当我们知道什么是 Galois 群 时，我们才能理解这个条件。

为此，我建议快速回顾一下域的 代数闭包 是什么。

Galois 群 是一个群，它的元素是 函数——准确地说是 自同构。这只是一个花哨的名称，用来称呼将集合的元素映射到同一集合的另一个元素的双射函数。可以说，它们“打乱了事物”。

但不是任何自同构集合——它是所有这些自同构的集合，这些自同构 固定 基础域 K 中的元素（意味着它们的行为就像 单位），同时它们打乱了代数闭包 K̄ 中的元素。像这样：

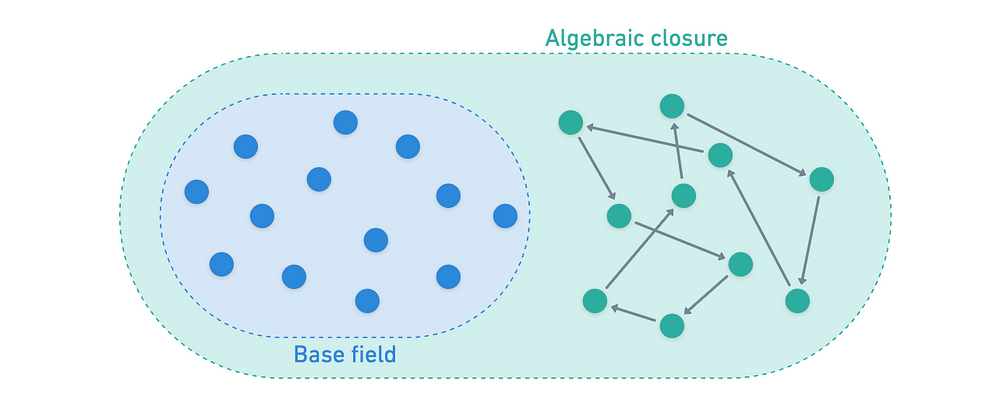
我们将该群表示为 Gal(K̄/K)。

在这一点上，我假设你正在问自己“但是，Frank，我为什么要关心这个？”。

事情是这样的：我们可以证明曲线和有理函数之间的交点需要以 Galois 群 Gal(ℚ̄/ℚ) 的 Galois 共轭 形式出现——其中 ℚ 是有理数。这意味着所有点要么是 基础域 的元素，要么都属于 代数闭包（但不属于基础域）。

或者用简单的英语来说：要么它们 都是有理点，要么它们 都是无理点。没有中间地带！

实际上，这并不完全正确，但为了今天，这种简化是可以接受的。

Galois 共轭 更精确的定义是，交点集合在群的作用下是 不变的，最终有点像我们刚才所说的。

证明这一点非常复杂。你可以在像 这本 这样的教科书中找到更多信息，但为了我们的目标，我认为我们可以直接接受这个简单的结论。此外，这里有一个关于 Galois 理论 及其其他一些应用的有趣视频。

好了，让我们回到现实。我将重复这个数学分支的结论：

有理函数和曲线的所有交点要么都是有理的，要么都是无理的。

很自然地，在我们圆的例子中，由于我们从一个有理点开始，并通过它绘制了一条有理函数（直线），因此另一个交点 肯定 是有理的。有趣的是，我们可以 无限次 地重复这个过程。

这个过程非常类似于 球面投影。顺便说一句，这看起来像是一个简单的方法，但实际上是由像 [Henri Poincaré](https://en.wikipedia.org...