Uniswap v3 的流动性提供者策略:损失与再平衡 (LVR)
- atise_
- 发布于 2024-03-19 11:29
- 阅读 1711
本文介绍了LVR(Loss Versus Rebalancing)的概念,它是一种评估流动性提供者(LP)盈亏的指标,不同于分歧损失(Divergence Loss)。LVR代表了套利者可以从系统中提取的最大价值,以LP为代价。文章深入探讨了LVR的假设、计算方式,以及降低LVR的策略,并讨论了LVR与分歧损失之间的联系与区别,强调了LVR在理解LP运作中的重要性。
本篇是 系列文章 中的一篇,讨论了 loss versus rebalancing (LVR),其背后的假设以及一些缓解方法。LVR是思考 LP 盈亏的另一种方式,与分歧损失指标不同,但与之互补。它代表了套利者可以从系统中提取的价值上限,以 LP 为代价。

LVR 介绍
LVR (发音为 “lever”) 的概念来自哥伦比亚大学的一个学术研究小组。
作者从观察到分歧损失 (DL),即试图击败 HODL,不一定是 LP 盈亏的最佳基准开始。事实上,DL 混合了两种不同的东西:
- 市场风险。LP 在创建流动性头寸时,以固定的比例添加资产,但随着资产相对价格的变化,这种比例会随着时间的推移而变化。因此,LP 很可能对资产的风险敞口与 hodler 不同,即使它们都以相同的资产比例开始。LP 可能因为这种对市场价格的不同风险敞口而表现优于或低于 hodler。LP 拥有相同资产比例的唯一情况是,当价格恢复到起始价格时;在其他情况下,LP 具有不同的市场风险。
- 来自特定交易函数的风险,与资金池资产相关,与 AMM 的负 Gamma 相关,以及 LP 头寸的被动性。简而言之,现有的 AMM 迫使 LP 以过时的价格出售其资产,这可能会被套利者利用。
这些风险可以在很大程度上被对冲掉——当然市场风险可以,正如上一篇文章所示。但是,对冲不是免费的。事实上,对冲成本与头寸的负 Gamma 值成正比:
- 对冲全范围头寸相对便宜;
- 对冲宽范围集中流动性 (CL) 头寸更昂贵;
- 对冲窄范围 CL 头寸最昂贵。
LVR 旨在将第二种风险——AMM 特定的和头寸特定的风险——隔离在一个不受市场风险影响的指标中。LVR 与 LP 头寸的 Gamma 成正比。
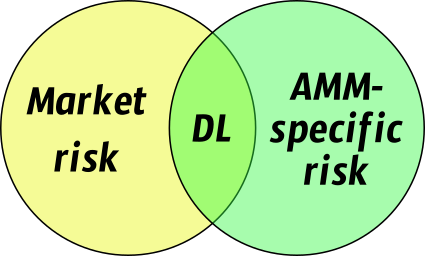
分歧损失混合了两件事:市场风险(可以通过使用借入的资产进行对冲)和另一种 AMM 特定的风险,这种风险来自 AMM 本身的交易功能,并且不能以相同的方式进行对冲。
此外,分歧损失不取决于价格从初始点到最终点所采取的路径。直观地说,这两种情况截然不同:
- 价格剧烈波动,但恢复到起点。
- 价格保持稳定。
在这两种情况下,分歧损失都为零。但是,如果价格波动,风险和机会成本都会更高。显然,波动性大的交易对 LP 应该获得更高的费用补偿,以便公平地评估额外的风险。LVR 指标旨在捕捉这种直觉。
LVR 论文从一个简单的等式开始:
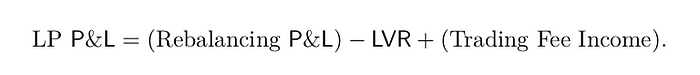
作者研究了一个潜在的基准投资组合,该投资组合与 LP 的资产构成相匹配,但在 CEX 上进行交易。其思想是,每当价格发生变化时,CEX 投资组合都会出售其中一种资产并购买另一种资产,以便与 LP 资产的构成保持同步。当然,再平衡投资组合也面临负 Gamma,预计会比非再平衡 HODL 投资组合损失更多。这使得再平衡投资组合比 HODL 投资组合更适合作为 LP 头寸的比较目标。
这个再平衡投资组合的利润由上面等式中的 “再平衡 P&L” 描述。如果没有掉期费用,那么 LP 相对于这个基准头寸将会出现损失,因为 LP 以过时的价格“交易”,并且他们的资产被套利者交换。这种损失会随着时间的推移而累积,被称为 LVR。
在现实世界的 DEX 中,LP 确实通过套利者支付的掉期费用收回了部分损失(请参阅下面的模拟)。事实上,在 0.3% 和 1.0% 的资金池中,如果资金池中的流动性足够深,大部分损失可以被收回。从实际角度来看,最好将其称为“成本”而不是“损失”,并记住 LVR 指标描述了损失的理论上限。
示例场景
Bob 在 Uniswap v3 1% 费用池上提供 ETH/USDC 流动性,价格范围为每个 ETH 1000 美元到 1100 美元。初始价格为 1000 美元,Bob 将 1 个 ETH 放入资金池。
当 CEX 中的价格变为 1100 美元时,Uniswap 中的价格对套利变得具有吸引力。一个成熟的做市商在 Uniswap 上购买 ETH 并在 CEX 上出售 ETH,直到 Uniswap 上的 ETH 价格变为 1100 美元。Bob 以 sqrt(1100 * 1000) = ~1049 USDC 的平均价格出售了他的 ETH,这现在是他在资金池中的资本(没有剩余的 ETH),此外还有他收取的 10.49 USDC 的费用。
Alice 最初也有 1 个 ETH,价值 1000 USDC,但她将其保存在她的钱包中。当 ETH 价格达到 1100 美元时,她在 CEX 上出售它,由于某种原因,该 CEX 没有费用,并且以该确切价格提供了一个愿意的买家。她最终获得了 1100 USDC。
LVR 为 1100–1049=51 USDC。由于它大于 Bob 收取的费用,因此根据此模型,他没有盈利。
现在价格恢复到 1000 美元。Bob 比他开始时多了 20.98 美元,并且没有分歧损失:2.1% 的利润。与此同时,Alice 现在购买了 1.1 个 ETH,相当于 10% 的利润,高于 Bob 的利润。
更深入的 LVR
作者还介绍了瞬时 LRV 的概念。这被理解为每无限小时间单位的 LVR。它与以下因素成正比:
- 价格波动率的平方 (σ ²)。
- LP 头寸的 Gamma,它取决于 AMM 的交易函数和头寸的集中因子。

LVR、资产波动率、价格和 AMM 的 Gamma 之间的关系
显然,在现实世界中,LP 还会收取交易费用,而再平衡投资组合则不会。在此模型中,如果 LP 的费用大于 LVR,则认为 LP 是盈利的,否则则认为 LP 是无利可图的。
作者使用资金池价值函数的二阶导数,在等式中写为 V’’(P)。这是 LP 头寸的 Gamma,在上篇文章中进行了分析。从数学上讲,全范围 Uniswap v2 式头寸的 Gamma 与负 √R³ 成反比,其中 R 是波动性资产的价格回报:即,相对于创建头寸时的初始价格的价格变化。
总而言之,LVR 随着波动率和 Gamma 的增长而增长:例如,波动率增加 2 倍将导致 LVR 高 4 倍。

如果假设 LVR 基准,则 v2 资金池 / v3 全范围头寸的盈利能力阈值
上图显示了 Uniswap v2 式全范围头寸的 LVR 估算。请记住:如果 fee_return > LVR,则认为 LP 是盈利的。
下图显示了 LP 盈利能力取决于 σ 和费用 APR。费用 APR=0% 和掉期费用 f 的模拟结果显示损失约为 σ²/ 8,正如分析模型所预期的那样(在图中显示为虚线)。作为参考,自 2020 年以来 ETH 的年度 σ 为 ~0.95 -> 全范围头寸抵消损失所需的费用 APR 为 ~11.4%。
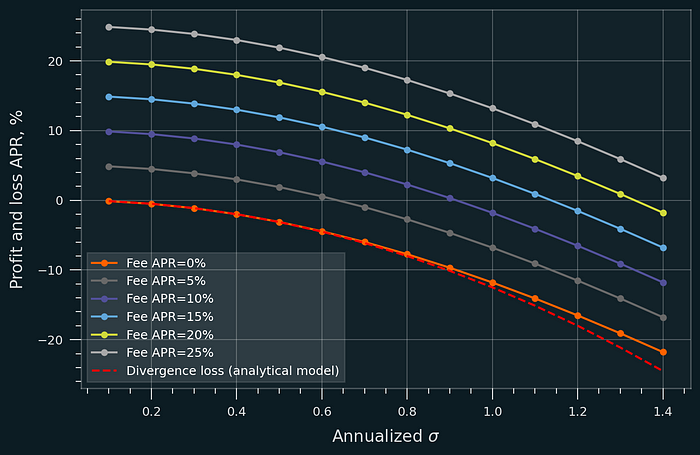
全范围头寸的预期分歧损失(== LVR)。资产的年度波动率 (σ) 越高,预期的分歧损失越高。需要高费用 APR 才能补偿预期损失。LVR 与分歧损失的预期价值相匹配:σ²/8。西格玛越大 -> 需要更多模拟 -> 模型误差越大。没有价格漂移 (μ=0) 的资产的模拟结果。
LVR 和 DL - 它们有那么不同吗?
如果你阅读过大量与 AMM 相关的研究,那么 σ²/8 值可能很熟悉。事实上,这也是在分歧损失模型下,头寸盈利需要收取的最低费用金额。有关 Uniswap 中分歧损失的预期价值,请参见此处(v2 和 v3)和此处(v3)。
Alexander Nezlobin 的 Medium 上有一篇 有趣的分析 关于 LVR 和分歧损失之间的联系(Twitter 上也有)。他的分析和模拟证实,LVR 的预期值与分歧损失的预期值相同。但是,他表明 LVR 的方差小于分歧损失。
LVR 和 EV(DL) 之间的这种相等是一个有趣的结果,尽管 LVR 和 DL 的实际实现形式截然不同。后者根本不取决于价格路径,并且具有 LVR 未包含的市场风险组成部分。
虽然在某些情况下 LVR 可以替换为 EV(DL),但并非总是如此。例如,让我们假设一对稳定币,它们总是恢复到它们的初始价格,但在相对价值上具有随机振荡。分歧损失的预期值接近于零,而 LVR,正如直观理解的那样,会随着时间的推移而增长。
我需要强调一个警告:我们需要考虑分歧损失的预期价值,而不是分歧损失本身。前者取决于波动率,后者仅取决于初始价格和最终价格。
LVR 背后的假设
-
存在 CEX 或其他具有更深流动性的替代场所,价格发现在这里发生。 这对于许多长尾资产来说并非如此,这些资产主要或专门在 Uniswap 上交易。再平衡投资组合对于这些资产不存在。虽然仍然可以计算这些资产的 LVR 值,但它缺乏实际意义。
-
存在 LP、“不知情的交易者” 和套利者。套利者进行交易而不支付交易费用。 这是一种技术简化,对结果产生一定影响;作者的 后续论文 显示了在更实际的模型中,当套利者也被要求支付费用时会发生什么。
首先,我使用 0.3% 的掉期费用以及实际的区块时间和交易成本进行了快速价格模拟。结果表明,LVR 的很大一部分被捕获为流动性提供者费用。
- 如果交易是免费的(零固定掉期成本),那么 LVR 的很大一部分会立即通过套利交易中的 LP 费用来补偿。确切的金额取决于的掉期费用,但如图所示,它可以达到 80-90%(对于 0.3% 的掉期费用池)。
- 如果交易具有非零执行费用,那么重新捕获的 LVR 比例会下降,因为套利交易频率会大大降低。
- 重新捕获的 LVR 也取决于资金池中的掉期费用。
请参见下图,但对下图中的 x 轴持保留态度:Tx 费用的确切影响取决于资金池中的流动性深度:流动性深 10 倍与交易费用便宜 10 倍具有相同的效果。
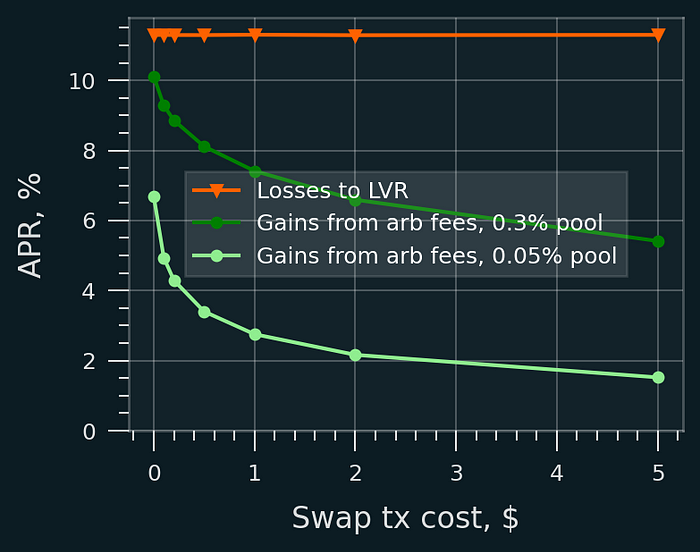
模拟参数:流动性池具有 100 万美元的资产价值(按照 Uniswap 标准来看,属于中小型)、0.3% 的掉期费用、12 秒的区块时间、μ=0、每日 σ=0.05 (类似于 ETH)。
- 套利者和 LP 进行零和博弈。 只有当我们没有向游戏中添加任何其他参与者时,情况才是如此,但如果我们将市场视为一个整体,情况可能会发生变化。例如,套利者必须支付交易费用,这有利于 ETH 质押者和持有者等第三方。但是,一个更有趣的问题是,由于套利,LP 是否总是比持有者更糟糕?
一个简单的情况是一对稳定币,它们只有随机的价格波动。LP 在这里会击败持有者:每当相互价格有足够大的波动时(即,偏离超过资金池的费用率 + 交易成本),LP 都会从套利者那里赚取费用。
但是,即使对于波动性大的资产池,LP 也可以击败 HODL 吗?假设最坏的情况是只有套利者在交易该交易对?(即,所有掉期交易量都是“有毒流量”。)答案取决于市场状况,但预期值分析可能为负数。Paradigm 网站上 2020 年的一篇博文声称,即使在这种情况下,LPing 也可能比持有好得多。具体来说,他们在两个特定假设下证明了这一点:首先,波动性资产的价格随着时间的推移而上涨;其次,波动率在特定范围内(高,但不太高)。但是,有些人指出他们的 数学模型 可能存在一些问题。不幸的是,最初的博文现在似乎已被删除,因为 Paradigm 已经重组了他们的网页。我无法评论这些结果的准确性,但这是 我讨论它们的 Twitter 话题 。
-
资产价格遵循几何布朗运动。 从概念上讲,LVR 仍然适用于不同的价格模型,但是,如果违反了模型的假设,则论文中提出的 LVR 的确切值可能不正确。但是,作者后来扩展了他们的工作,还表明即使波动率不是常数,而是随时间变化的过程,结果仍然成立,这是一个更现实的假设。
-
LP 已经对冲了他们对价格风险的敞口。 这显然是一个很大的假设,对于许多 LP 来说并非如此。
缓解 LVR
LVR 本质上是由 LP 以过时的价格“交易” 引起的。可以通过降低价格的过时程度或增加 LP 的费用收入来缓解它。下面是一些想法。
- 通过减少区块时间来增加套利交易频率。虽然预计较短的区块时间不会减少 LVR,但由于更高的掉期交易量,它们可能会增加 LP 收取的掉期费用。但是,我的模拟未能证实 LP 在实际条件下有任何显着的好处!请参见下图。虽然有一些现有的模拟显示了显着的好处,但它们使用的假设是交易费用(gas 成本)为零。
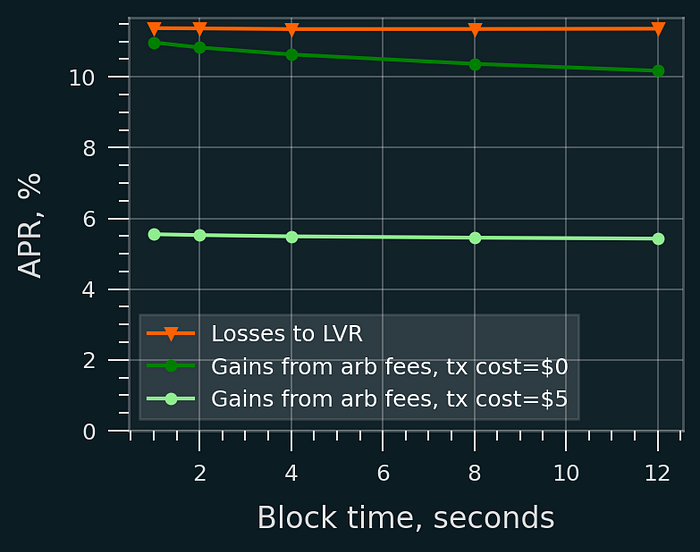
区块时间与费用利润。模拟结果。LVR 符合理论上预期的 ~12% 的年化价值,并且不依赖于区块时间。每日波动率 σ=0.05,价格漂移 μ=0。
只有当交易费用为零时,掉期费用似乎才取决于区块时间(请参见上图),从而允许套利者即使在可以获得最小利润时也进行交易。尽管如此,由于其他原因,短区块时间最终可能对 LP 更好。L2 (Arbitrum, Optimism) 和主网之间的经验比较将很有趣。
-
使用 CEX 来源的 预言机 来告诉资金池资产的“真实”价格。这需要在 AMM 本身中进行协议级别的更改,而且我真的不喜欢这种方法:它不够健壮、无许可,并且无法扩展到长尾资产。DeFi 的未来在于 无预言机的协议。
-
动态费用。虽然 Uniswap v1-v3 没有动态费用,但 LP 可以并且应该监控波动率,并在需要时将其流动性重新分配到更高的费用等级。在 v4 中,由于 hooks,将启用更高级的动态费用选项。
-
执行速度相关的费用。这个想法是惩罚必须快速执行的交易(套利交易),同时降低可以等待多个区块的交易(不知情的交易)的费用。这可能需要 AMM 级别的更改。
-
改变参与者之间的收益分配。例如,如果有一些方法可以捕获套利者支付的交易费用,并将它们直接支付给 LP,那么可以激励 LP 提供更多的流动性。通过 MEV 捕获来降低 LVR 在技术上是 可以在 Uniswap v4 中集成的,通过 hooks。
此外,专门为 DeFi 交易应用程序创建的 L2 或 L3 链可能开箱即用地支持此功能。Uniswap 链,有人要吗?
Paradigm 的 Dan Robinson 的一些其他想法在这里 这里 列出, 包括区分套利和非套利交易,以及更具体的 MEV 相关想法。
主要收获
- LVR 代表了在 AMM 中提供流动性的 LP 以成本可提取的最大套利价值。它似乎是由于 LP 以过时的价格交易造成的。LVR 的一部分作为 CEX 和 DEX 套利者的利润提取,一部分归区块构建者所有,另一部分由 LP 通过费用重新捕获。
- LVR 与波动性大的短尾(ETH/USDC、WBTC/USDC 等)交易对相关,尽管一些想法确实适用于稳定交易对和长尾资产。通常,LVR 假设套利者在 AMM 流动性池和价格发现区域(例如具有更深流动性的 CEX)之间进行交易。
- 分歧损失指标还包括市场风险,而 LVR 不包括该风险;相反,它侧重于 AMM 特定的风险,这些风险不像市场风险敞口那样容易对冲。
- 可以通过多种方式缓解 LVR,但其中大多数仅适用于协议和区块链设计者,而不适用于 LP 本身。
- LVR 是一个重要的概念,需要深入了解 LP。尽管如此,它并没有使分歧损失作为 LP 的关键指标过时。分歧损失的优点在于它使用 HODL 基准,这对于任何 LP 来说都是一个现实的替代选择。当然,没有理由让所有 LP 都收敛到单一标准:一刀切的方法是不现实的,因为 LP 有不同的目标。
致谢。 这项工作得到了 Uniswap 基金会 的财政支持。感谢 Jason Milionis 对草稿版本的解释和评论。
免责声明。 加粗 此帖子仅供一般信息参考。它不构成投资建议或购买或出售任何投资的建议或招揽,不应用于评估做出任何投资决定的优点。不应依赖它来进行会计、法律或税务建议或投资建议。本文是在作者的空闲时间撰写的,与他的专业活动或他的雇主无关。此帖子反映了作者当前的观点,这些观点可能会发生变化,而不会进行更新。
- 原文链接: atise.medium.com/liquidi...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 顶级DeFi交易所:理解去中心化交易基础设施 - CoW DAO 275 浏览
- Uniswap V2 — 理解DeFi协议的完整指南 71 浏览
- 在Polymarket上交易所需的数学知识(完整指南)- 第二部分 484 浏览
- 为了理解,你必须创造,或我们为什么构建一个开源的 Solana 聚合器 463 浏览
- 在Polymarket上交易所需的数学(完整路线图) 473 浏览
- 第 19 章: NFT 交易市场 1817 浏览
- 2026年你需要了解的加密货币仅挂单 - CoW DAO 461 浏览
- Sudoswap 正在升级 ♨️ 399 浏览
- 深入浅出流动性池:手把手教你写出第一个去中心化做市商合约 840 浏览
- 第4章:流动性挖矿 1749 浏览
- 第3章:去中心化交易所 2603 浏览
- Solana 上 Prop AMM 的解析 807 浏览

