基于RLNC的分片替代DAS概念

本文提出了一种基于RLNC（随机线性网络编码）和Pedersen承诺的以太坊数据可用性（DAS）方案。该方案将原始数据分割成N个向量，使用RLNC进行编码并通过Pedersen承诺进行验证。每个节点只需下载和保管1/S的原始数据，通过节点间交换随机线性组合向量，当满足特定条件时完成数据采样，成为活跃节点。

非常感谢 Alex、Csaba、Dmitry、Mikhail 和 Potuz 的富有成果的讨论和撰写审查

摘要

以太坊目前的 DAS 方法基于里德-所罗门纠删码 + KZG 承诺。新的方案（此处描述，由 @potuz 撰写的 以太坊中更快的区块/blob 传播）引入了另一对：RLNC（随机线性网络编码）纠删码 + Pedersen 承诺。它具有良好的属性，可以用于考虑替代的数据可用性方法。

本文档中概述的协议主要概述了基于 RLNC 的数据可用性设计可能是什么样子。这里使用的概念尚未经过充分检查，更不用说经过正式证明了。无论如何，如果这些概念被证明是正确的，该算法可以作为原型设计的基础。如果其中一些概念被证明是不正确的，我们可以调整算法，或者考虑调整或替换它们。

本文档中的推理在几个方面与 @Csaba 最近的帖子重叠：通过 FullDASv2（带有 getBlobs、mempool 编码，可能还有 RLC）加速 blob 扩展。

要探索完整的上下文，包括推理和讨论评论，请参阅本文档的扩展版本：https://hackmd.io/@nashatyrev/Bku-ELAA1e_

简介

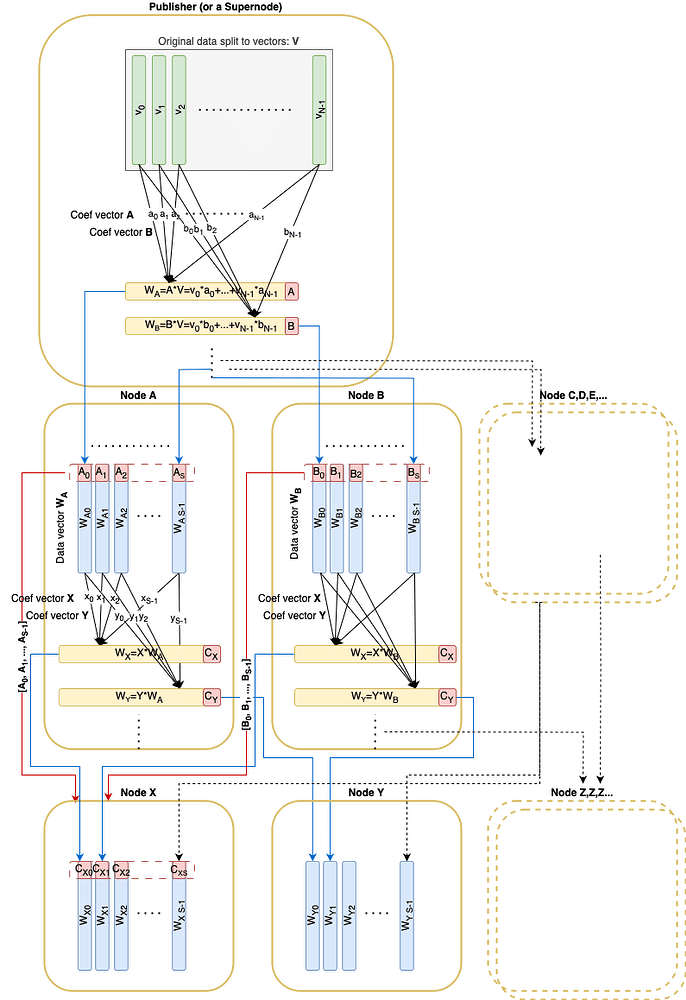
与文档 以太坊中更快的区块/blob 传播 非常相似，原始数据被拆分为 N 个向量 v_1, \dots, v_N，这些向量位于 \mathbb{F}_p 域上。这些向量可以使用 RLNC 进行编码，并通过包含在区块中的 Pedersen 承诺（大小为 32 \times N）进行承诺。给定承诺及其相关的系数，可以验证任何线性组合。

我们还假设系数可能来自一个更小的子域 \mathbb{C}_q，其大小可能小到一个字节——甚至是一位（免责声明：从最新的讨论来看，尚未确认我们可以在具有如此小的子域的域上拥有安全的 EC）。

让我们还引入分片因子 S：任何常规节点都需要下载并保管 1/S 的原始数据大小。

假设有一个固定的分片因子 S，让我们取原始向量的总数为 N = S^2

简要协议概述

Pedersen 承诺（大小为 32*N）发布在相应的区块中。

在传播过程中，每个节点从其对等节点接收伪随机线性组合向量。

  • 该算法描述了一种非交互式方法，其中随机系数是从接收者的 nodeId 确定性地派生的，并且使用了 RREF 矩阵技巧（免责声明：RREF 技巧并没有被严格证明可以安全工作，但是有一个 示例 可以作为证明的起点）。
  • 还有一个可用的回退选项：一种交互式方法，其中响应者首先公开其源系数，然后请求者使用本地生成的随机系数请求线性组合。

每个发送的线性组合向量都附有该向量随机采样的子空间的基向量。这些基向量必须形成 RREF 形式的矩阵。此条件确保远程对等节点确实拥有所声明子空间的基向量。

节点继续采样，直到满足以下两个条件：

  • 所有接收到的基向量跨越完整的 N 维空间
  • 至少收到了 S 个用于保管的向量

之后，节点完成采样并成为“活动”节点，可供其他节点用于采样。

DA-RLNC.drawio\ DA-RLNC.drawio796×1158 93.8 KB

注意

下面的类 Python 代码片段仅用于说明目的，目前不打算编译和执行。一些显而易见的或类似库的函数目前缺乏实现。

类型

令数据向量元素来自有限域 \mathbb{F}_p，该域可以大致映射到 32 字节


type FScalar

令系数 \mathbb{C}_q 来自 \mathbb{F}_p 的子域（或等于）


type CScalar

令单个数据向量具有来自 \mathbb{F}_p 的 VECTOR_LEN 元素


type DataVector = Vector[FScalar, VECTOR_LEN]

令整个数据分割成 N 个原始 DataVector：


type OriginalData = Vector[DataVector, N]

派生 DataVector 是原始 DataVector 的线性组合。由于原始向量只是派生向量的一个特例，我们将不再区分它们。

为了根据承诺验证 DataVector，应该知道其线性组合系数：


type ProofVector = Vector[CScalar, N]

还有一组略有不同的系数，用于从现有 DataVector 派生新向量时使用：


type CombineVector = List[CScalar]

结构体

一个数据向量，附带有其线性组合系数


class DataAndProof:
    data_vector: DataVector
    proof: ProofVector

唯一用于传播的消息是


class DaMessage:
    data_vector: DataVector
    # 用于验证的 coefVector 是派生的
    orig_coeff_vectors: List[CombineVector]
    seq_no: Int

有一个用于区块数据的临时存储：


class BlockDaStore:
    custody: List[DataAndProof]
    sample_matrix: List[ProofVector]

    # 承诺首先从相应的区块初始化
    commitment: Vector[RistrettoPoint]

函数

让函数 random_coef 使用种子 (nodeId, seq_no) 生成一个确定性随机系数向量：


def random_coef(node_id: UInt256, length: int, seq_no: int) -> CombineVector

让我们定义实用函数来计算线性组合：


def linear_combination(
        vectors: Sequence[DataVector],
        coefficients: CombineVector) -> DataVector
def linear_combination(
        vectors: Sequence[ProofVector],
        coefficients: CombineVector) -> ProofVector

函数同时对 DataVector 和 ProofVector 执行线性运算，以将 ProofVector 转换为 RREF：


def to_rref(data_vectors: Sequence[DataAndProof]) -> Sequence[DataAndProof]
def is_rref(proofs: Sequence[ProofVector]) -> bool

该函数从用于特定对等节点的现有保管向量创建一个新的确定性随机消息：


def create_da_message(
        da_store: BlockDaStore
        receiver_node_id: uint256,
        seq_no: int) -> DaMessage:
    rref_custody = to_rref(da_store.custody)
    rref_custody_data = [e.data_vector for e in rref_custody]
    rref_custody_proofs = [e.proof for e in rref_custody]
    rnd_coefs = random_coef(receiver_node_id, len(rref_custody), seq_no)
    data_vector = linear_combination(rref_custody_data, rnd_coefs)
    return DaMessage(data_vector, rref_custody_proofs, seq_no)

计算数据向量系数的秩。秩等于 N 意味着可以从数据向量恢复原始数据。


def rank(proof_matrix: Sequence[ProofVector]) -> int

发布

发布者应将数据切片为向量以获得 OriginalData。

在传播数据本身之前，发布者应计算 Pedersen 承诺（大小为 32 * N），构建并发布包含这些承诺的区块。

然后，发布者应该用数据向量（原始）及其“证明”填充保管库，这些证明只是标准基的元素：[1, 0, 0, ..., 0], [0, 1, 0, ..., 0]：


def init_da_store(data: OriginalData, da_store: BlockDaStore):
    for i,v in enumerate(data):
        e_proof = ProofVector(
            [CScalar(1) if index == i else CScalar(0) for index in range(size)]
        )
        da_store.custody += DataAndProof(v, eproof)

发布过程与传播过程基本相同，只是发布者在单个回合中向单个对等节点发送 S 条消息，而不是在传播过程中仅发送 1 条消息。


def publish(da_store: BlockDaStore, mesh: Sequence[Peer]):
    for peer in mesh:
        for seq_no in range(S):
            peer.send(
                create_da_message(da_store, peer.node_id, seq_no)
            )

接收

假设相应的区块已收到，并且在收到 message: DaMessage 之前已填充 BlockDaStore.commitment。

从原始向量派生 ProofVector：


def derive_proof_vector(myNodeId: uint256, message: DaMessage) -> ProofVector:
    lin_c = randomCoef(
        myNodeId,
        len(message.orig_coefficients),
        message.seq_no)
    return linear_combination(message.orig_coefficients, lin_c)
验证

首先验证消息：


def validate_message(message: DaMessage, da_store: BlockDaStore):
    # 验证原始系数是否为简化行梯形形式
    assert is_rref(message.orig_coefficients)
    # 验证源向量是否线性独立
    assert rank(message.orig_coefficients) == len(message.orig_coefficients)
    # 验证 Pedersen 承诺
    proof = derive_proof_vector(my_node_id, message)
    validate_pedersen(message.data_vector, da_store.commitment, proof)
存储

收到的 DataVector 被添加到保管库。

sample_matrix 正在累积所有原始系数，并且一旦矩阵秩达到 N，采样过程就会成功


def process_message(message: DaMessage, da_store: BlockDaStore) -> boolean:
    da_store.custody += DataAndProof(
        message.data_vector,
        derive_proof_vector(my_node_id, message)
    )
    da_store.sample_matrix += message.orig_coefficients
    is_sampled = N == rank(da_store.sample_matrix)
    return is_sampled

is_sampled == true 意味着我们[几乎] 100% 确定向我们发送消息的对等节点共同拥有 100% 的信息来恢复数据。

传播

当 process_message() 返回 True 时，这意味着采样成功，并且保管库已填充足够数量的向量。从现在开始，节点可以开始创建和传播自己的向量。

我们将向量发送到网格中尚未向我们发送任何向量的每个对等节点：


## mesh: 此处为尚未发送任何向量的对等节点的集合
def propagate(da_store: BlockDaStore, mesh: Sequence[Peer]):
    for peer in mesh:
            peer.send(
                create_da_message(da_store, peer.node_id, 0)
            )

可行性

让我们根据 S 和 |\mathbb{C}_q|（系数的大小）概述一些数字，假设原始数据大小为 32Mb：

S sizeOf(C) (bits) N 向量大小 (Kb) 承诺大小 (Kb) Msg coefs size (Kb) Msg 开销 (%%)
8 1 64 512 2 0.0625 0.01%
8 8 64 512 2 0.5 0.10%
8 256 64 512 2 16 3.13%
16 1 256 128 8 0.5 0.39%
16 8 256 128 8 4 3.13%
16 256 256 128 8 128 100.00%
32 1 1024 32 32 4 12.50%
32 8 1024 32 32 32 100.00%
32 256 1024 32 32 1024 3200.00%
64 1 4096 8 128 32 400.00%
64 8 4096 8 128 256 3200.00%
64 256 4096 8 128 8192 102400.00%

根据这些数字，基本上不可能将此算法与 S \ge 64 一起使用。如果没有选项使用小系数（1 或 8 位），那么由于系数大小的开销，S = 8 是有意义的最大分片因子。（使用 S = 16，最小节点下载吞吐量将与 S = 8 相同。）

优点和缺点

优点

  • 要传播、保管和采样的数据总大小是原始数据大小的 x1（+ 系数开销，如果可以使用小系数，则可以很小）（相比之下，PeerDAS 为 x2，FullDAS 为 x4）
  • 我们可能可以将“分片因子”S 设置为 32 那么大（或者通过对算法进行其他一些修改，甚至可能更大），这意味着每个节点只需要下载和保管原始数据大小的 1/S。（与当前 PeerDAS 方法中的 1/8 相比：来自 64 个原始数据的 8 列）
  • 数据是可用的，并且可以通过任何 S 个常规诚实节点成功执行采样来恢复数据
  • 可以通过任何 S 个常规节点执行采样（与当前的 DAS 相比，当前的 DAS 要求采样节点具有来自不同 DAS 子网的各种对等节点）
  • “你采样什么，你就保管和服务什么”的方法（类似于 PeerDAS 子网采样，但不同于全分片对等节点采样）。此处 描述了关于对等节点采样方法的担忧
  • 由于未涉及列切片，因此单独的 blob 可能只是跨越几个原始数据向量，因此采样过程可能会有效地受益于 EL blob 交易池（又名 engine_getBlobs()）
  • 没有可能容易受到女巫攻击的较小子网
  • 由于节点需要来自任何对等节点的 S 条消息，并且使用了 RLNC 编码，因此传输级别上的数据重复可能会更低
  • RLNC + Pedersen 可能比 RS + KZG 消耗更少的资源

缺点

  • 承诺和证明大小随着分片系数 S 的增加而呈二次方增长。
  • 如果无法使用较小的系数（未证明是安全的），那么只有 S=8 是可行的。
  • 仍然需要估计传播延迟，因为节点可能只在完成自己的采样后才传播数据
  • 对于乐观情况，用于采样的最小对等节点数为 32（与 PeerDAS 中的 8 个相比）

需要证明的陈述

上面的算法依赖于许多[尚未明确的]陈述，这些陈述目前需要证明：

  1. 超节点返回的具有请求的随机系数的有效线性组合证明了响应节点可以访问完整数据（足以恢复的向量）。这个陈述看起来并不难证明
  2. 如果一个全节点声称它具有形成系数子空间的基向量，那么如果一个节点从此子空间中请求一个随机向量并获得一个有效的数据向量，那么它证明了响应节点确实具有所声明子空间的基向量。该证明可以是陈述 (1) 的概括
  3. \mathbb{F}_p 上带有子域 \mathbb{C}_2 的 EC 是有意义且安全的。（根据最新的讨论，这似乎是不正确的）
  4. 用于零-RRT 采样的 RREF 基形式技巧实际上有效。

（此示例 可以提供对该陈述有效性的一些直觉）

  1. 所描述的算法为完整的 N 维空间在诚实节点上产生均匀分布的基向量。存在一个非常小的 E（大约为 1-3），使得任何随机选择的 S + E 个节点的基向量的秩将以某个“非常高”的概率为 N。在拜占庭环境中也应该如此
  • 原文链接： ethresear.ch/t/alternati...
  • 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
以太坊中文
以太坊中文
以太坊中文， 用中文传播以太坊的最新进展

以太坊中文

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！