区块链中的数学- BLS密钥聚合

写在前面

上一节简要概述了BLS签名机制，具体实现起来有很多细节，如哈希消息到曲线上的点。 本文原计划讲BLS依赖的基础知识部分，如双线性映射，但既然已经讲了签名，就先把签名相关的应用部分说完，才回头看其原理！ 所谓“观其大略” 再究其细节！

最近几篇的思路大致为：BLS签名介绍 --> 密钥聚合 --> BLS门限签名 -->BLS基石（双线性函数）和配对

BLS密钥聚合

上一篇说了BLS实现签名聚合的情况，把涉及到的签名聚合在一起，但是公钥还必须使用所有公钥，没有聚合公钥部分。

根据前面多签的介绍，可以知道使用多重签名的地址，会对同一笔交易用不同的密钥进行签名。我们也介绍过Schnorr 签名算法来聚合密钥，把所有公钥和签名聚合成单个公钥和签名。 接下来，以3-3多重签名方案为例来说明BLS聚合密钥过程。

一种简单的聚合方法，把所有的签名和公钥加起来。这样，签名聚合结果为 $S =S_1 +S_2 +S_3$ ，密钥聚合结果为 $P =P_1+P_2+P_3 $。令q为消息m哈希映射到曲线上的点，是一个确定的值。可以验证以下等式成立：

e(G, S) = e(P, q)

验证如下：

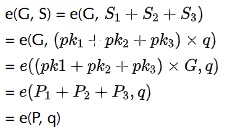
符号同上文，利用配对函数e的性质。

抗密钥攻击聚合

上述的方案理论上可行，但实际上可能受到密钥攻击，例如伪造签名，如何防范呢？

一种方法是要求每个签名参与者证明它拥有公钥对应的私钥（用私钥给公钥签名或者随机指定消息签名）。 另一种方法是加入非线性系数，使得攻击难以实施。当然就不能使用上面提到的简单的将多个公钥和签名相加的方法，而是将它们分别乘以某个系数后再相加：

$S =a_1 × S_1 +a_2 × S_2 + a_3 × S_3$

$P =a_1 × P_1 + a_2 × P_2 + a_3 × P_3$

公式中签名和公钥的系数，可以通过签名者以及其它所有参与者的公钥计算得出，公式如下：

$a_i = hash(P_i,P_1,P_2,P_3)$

最简单的做法是将签名者的公钥和所有参与者公钥拼接在一起： $a_i = hash(P_i||P_1||P_2||P_3)$

此时，上面的验证公式依然成立。虽然多了系数 $a_i$，但计算逻辑未变。

具体代码实现可以多种，只要是可验证的,确定性的即可。

单就该方案的好处是，无需多轮通信，只需知晓其它签名者的信息即可。它可比 Schnorr 算法（需要 3 轮通信）的多重签名方案简单。且不依赖随机性，是一种具有完全确定性的签名算法。

小结

改进的密钥聚合的算法是如何防止伪签名的呢? 本质上增加了公钥的可验证性 你的就是你的，不是你的就不是你的，！

本文中提到第一种方案可能存在密钥攻击，究竟是如何攻击呢？下一篇继续介绍！

欢迎关注公众号：blocksight

相关阅读：

区块链中的数学 - BLS数字签名 BLS签名及验证

区块链中的数学 - 参与者 < 门限值t的密钥更新Amir Herzberg方案 Amir Herzberg改进方案

区块链中的数学 - Amir Herzberg动态密钥共享 Amir Herzberg动态密钥分享方案

区块链中的数学 - Feldman的可验证的密钥分享 Feldman可验证密钥分享方案

区块链中的数学 - Shamir密钥分享 Shamir原始的密钥分享方案

区块链中的数学 - 比特币使用的多签方式 比特币多签和Schnorr聚合签名

区块链中的数学 - 随机数和伪签名 随机数与伪签名构造

区块链中的数学 - EdDSA签名机制 EdDSA的发展及优点

区块链中的数学 - Ed25519签名 Ed25519签名

区块链中的数学-ElGamal算法 ElGamal算法签名及验证&实例演练

区块链中的数学-VRF基于ECC公钥体制的证明验证过程 基于椭圆曲线的VRF证明验证过程

Schorr签名与椭圆曲线 Schorr签名与椭圆曲线

区块链中的数学-Uniwap自动化做市商核心算法解析 Uniwap核心算法解析（中）