多变量二次(MQ)签名方案： 对比 UOV 和MAYO签名方案
- billatnapier
- 发布于 1天前
- 阅读 64
本文介绍了后量子密码学中的多变量二次(MQ)签名方案，重点比较了UOV（Unbalanced Oil and Vinegar）和MAYO签名方案。UOV签名速度快、签名尺寸小，但是密钥尺寸太大。MAYO是UOV的变体，具有更小的公钥尺寸，在NIST的额外签名竞赛中表现出潜力。
加点 MAYO 吧，就像油和醋一样
我喜欢用于公钥签名的不平衡油和醋（Unbalanced Oil and Vinegar, UOV）方法。 基本上，它使用多元多项式问题，我们创建一个后门，以便我们能够使用 m 个等式快速求解 n 个变量（这些是多元多项式）。 在下面的示例中，我们使用私钥对消息进行签名，并使用公钥进行验证：
总的来说，UOV 具有出色的性能和签名大小，但密钥大小相当大（通常超过 50KB）。 以下是 Rainbow 的一个实现：
密钥大小如下：
私钥大小 = 51824
公钥大小 = 30096
签名大小 = 66我们可以看到密钥大小相当大，签名大小很小：
总的来说，这些密钥大小会使其在许多应用中无法使用，例如区块链应用。
方法 公钥大小 私钥大小 签名大小 安全级别
------------------------------------------------------------------------------------------------------
Crystals Dilithium 2 (格) 1,312 2,528 2,420 1 (128-bit) 格
Crystals Dilithium 3 1,952 4,000 3,293 3 (192-bit) 格
Crystals Dilithium 5 2,592 4,864 4,595 5 (256-bit) 格
Falcon 512 (格) 897 1,281 690 1 (128-bit) 格
Falcon 1024 1,793 2,305 1,330 5 (256-bit) 格
Rainbow Level Ia (油和醋) 161,600 103,648 66 1 (128-bit) 多元 (UOV)
Rainbow Level IIIa 861,400 611,300 164 3 (192-bit) 多元 (UOV)
Rainbow Level Vc 1,885,400 1,375,700 204 5 (256-bit) 多元 (UOV)
Sphincs SHA256-128f Simple 32 64 17,088 1 (128-bit) 基于哈希
Sphincs SHA256-192f Simple 48 96 35,664 3 (192-bit) 基于哈希
Sphincs SHA256-256f Simple 64 128 49,856 5 (256-bit) 基于哈希Rainbow V 的公钥大小超过 1MB，这简直太大了。 但是，现在我们有了 MAYO，它是油和醋方案的变体，公钥小得多。 我们可以看到，MAYO-1 的公钥大小只有 1,420 字节，私钥非常小，只有 24 字节 [ 这里 ]：
方法 安全级别 安全性 公钥 私钥 签名
-----------------------------------------------------------------------------------------------------
Dilithium2 2 SUF-CMA 1312 2528 2420
Dilithium3 3 SUF-CMA 1952 4000 3293
Dilithium5 5 SUF-CMA 2592 4864 4595
ML-DSA-44 2 SUF-CMA 1312 2560 2420
ML-DSA-65 3 SUF-CMA 1952 4032 3309
ML-DSA-87 5 SUF-CMA 2592 4896 4627
Falcon-512 1 EUF-CMA 897 1281 752
Falcon-1024 5 EUF-CMA 1793 2305 1462
MAYO-1 1 EUF-CMA 1420 24 454
MAYO-2 1 EUF-CMA 4912 24 186
MAYO-3 3 EUF-CMA 2986 32 681
MAYO-5 5 EUF-CMA 5554 40 964你可以在这里尝试使用 MAYO：
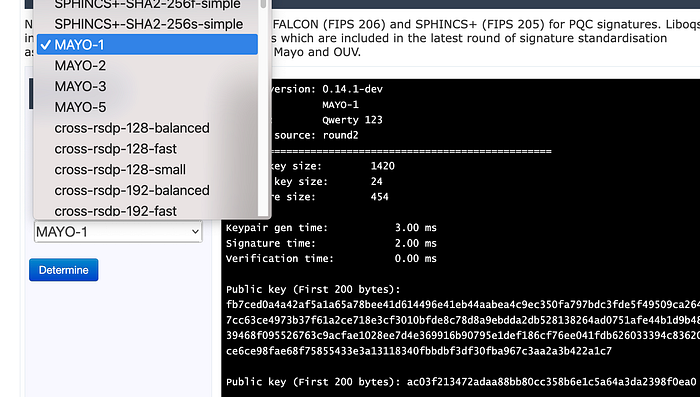
因此，MAYO 进入了 NIST 额外签名竞赛的第二轮，并希望像上一轮的 Rainbow 一样失败。 总的来说，油和醋方法看起来很棒，并且比格方法具有更强的安全性保证。
更多关于 MAYO 的细节请看这里：
基础知识
RSA 加密方法使用两个素数的乘积来创建一个公共模数 (N)。 不幸的是，如果我们使用量子计算机，N 的因式分解相当容易。 因此，NIST 现在正在寻找 RSA 和 El Gamal 等其他方法的替代方案，以适应量子计算机时代。
目前，我们通常使用对称加密（例如 AES）进行主要加密，然后使用非对称加密（例如 RSA）来保护对称密钥和/或证明身份。 通常，我们使用 RSA 对身份进行签名，例如使用私钥进行签名，然后使用相关的公钥来验证签名。
多元多项式问题现在应用于量子鲁棒密码学中，我们创建一个后门，以便我们能够使用 m 个等式快速求解 n 个变量（这些是多元多项式）。
可以使用的一种方案是不平衡油和醋方案，它由 J. Patarin 创建。 使用许多等式创建一个签名：
y 1= f( x 1, x 2… xn) y 2= f( x 1, x 2… xn)… ym = f( x 1, x 2… xn)
其中 y 1, y 2,… ym
是要签名的消息，其中 x 1, x 2… xn 是消息的签名。 作为一个简单的例子：
5 x+ 4y + 10 w + 9 z = 99
6 x + 3 y + 2 w + 3 z =38
8 x + 2 y + 7 w + z = 51
x + 9 y + 4 w + 6 z =57消息是 99、38、51 和 57，签名是 5、4、10 … 6。
- 原文链接： billatnapier.medium.com/...
- 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
