🚢 Succinct 发布：SP1 中优化的 bn254 & bls12-381 预编译
- Succinct
- 发布于 2024-10-08 14:48
- 阅读 84
Succinct 团队的实习生 Bhargav 在 SP1 上实现了 bn254 和 bls12-381 椭圆曲线运算的预编译，显著提升了 SP1 的 ZKVM 性能。这些预编译加速了 Groth16 和 PlonK-KZG 证明的验证，并优化了以太坊 ZK 轻客户端 SP1 Helios 的性能，同时还加速了revm中bn254配对。
TL;DR: 我们的实习生 "Bhargav the Great" 在他的暑期实习中狂热地编写 SP1 代码，并且 现在 Fred Ehrsam 在 X 上关注了他。
- 他发布了新的预编译，用于加速 bn254 和 bls12-381 椭圆曲线运算，这使得 SP1 成为目前唯一具有这些功能的、可用于生产环境的 zkVM。
- 这些预编译能够快速证明以下内容：
- 在 SP1 程序中验证 groth16 & plonk-kzg 证明
- 快速的 bls12-381 EC 运算，用于以太坊中所需的 KZG 和 blob 运算
- 快速的 bn254 运算和配对计算，用于证明 EVM 执行（使用 revm），这为 RSP 和 OP-Succinct 带来了巨大的性能提升。
- 使用 SP1 Helios 优化以太坊 ZK 轻客户端
- 你可以立即开始使用 SP1 v2.0.0 或 v3.0.0，如有任何问题，请 联系我们！
bn254、bls12-381 和 SP1 预编译的背景
bn254 和 bls12-381 椭圆曲线是以太坊生态系统中常用的椭圆曲线。许多协议使用 bls12-381 进行数字签名，例如以太坊的共识和各种 ZKP 协议（如 ZCash）。bn254 曲线非常流行，以至于它已被奉为以太坊的 预编译，并且通常用于 EVM 验证 Groth16 和 PlonK-KZG 证明。
bn254 和 bls12-381 在加密生态系统中的使用示例
| 曲线 | 应用 |
|---|---|
| bn254 | Groth16 证明验证 |
| PlonK-KZG 证明验证 | |
| revm bn254 预编译（加法、乘法、配对） | |
| bls12-381 | 以太坊轻客户端（验证验证者的聚合 bls12-381 签名） |
| 用于以太坊 blob 验证的 KZG 验证 |
由于它们在以太坊生态系统中的普遍性，这些椭圆曲线运算也常用于 SP1 程序中。但是，在 Rust 中实现的椭圆曲线算术在 SP1 内部的计算成本很高，导致证明生成时间较长。值得庆幸的是，SP1 的预编译解决了这个问题，它提供了主要的性能提升。
SP1 预编译来救援
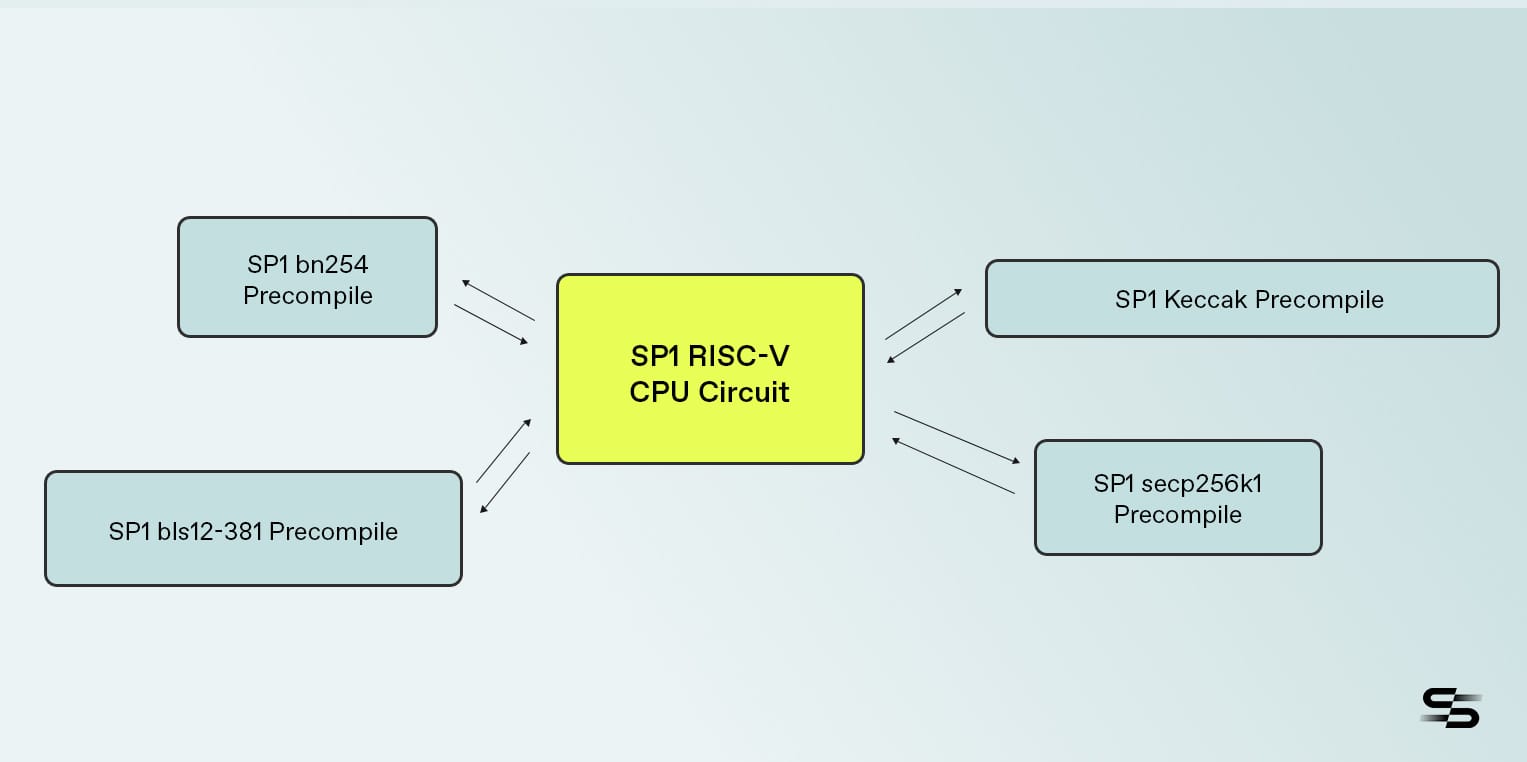
SP1 的预编译是专门的 STARK，旨在有效地计算通用操作，例如哈希函数或椭圆曲线运算。单个预编译调用用于代替执行执行复杂任务所需的许多单独的 CPU 指令。与我们的 RISC-V CPU 表所需的许多周期相比，专门的预编译电路在证明计算方面效率更高，后者会因需要将数据移入/移出寄存器和内存而产生开销，并且还会因容纳所有可能的指令而产生证明者开销。
通过显着减少 RISC-V 周期的数量，预编译通常会将证明的计算开销减少 几个数量级（查看附录中的基准）。
关于椭圆曲线运算的一个有趣的题外话
在传统的 CPU 执行环境中，在投影空间（P²）中进行椭圆曲线算术运算效率更高，因为有限域反演和平方根的成本很高。但是，在 zkVM 上下文中，这些原本代价高昂的运算的成本仅比字段乘法略高——这是“验证而不是执行”这一通用理念的直接结果。因此，我们只需要检查见证值是否确实是正确的平方根或逆，而不是在 SP1 内部显式查找该值。
使用极快的预编译降低周期数
极快的 groth16 + plonk-KZG 证明验证
使用我们的 bn254 预编译，我们构建了一个 sp1-snark-verifier 库，用于在 SP1 中验证 Groth16 或 PlonK 证明，这对于通用证明聚合很有用。SP1 本身也会生成 EVM 验证的 PlonK 证明的 Groth16 证明，你可以使用此库来使用 SP1 递归验证自身的证明！
使用 bn254 预编译可显着提高性能，对于 Groth16 和 PlonK 证明验证，性能均提高了约 20 倍。
| ZKP 系统 | 预编译前（周期） | 预编译后（周期） |
|---|---|---|
| PlonK 验证 | 187,227,852 | 8,078,761 |
| Groth16 验证 | 173,953,261 | 9,390,640 |
极快的 kzg-rs blob 验证
KZG 多项式承诺方案是一种密码学方法，用于有效地证明多项式求值。在以太坊中，EIP-4844 需要 KZG 承诺，这是最近的一项更新，通过临时“blob”数据类型实现了以太坊扩展。Blob 对于 Layer 2 汇总有效运行至关重要，因为它使它们能够发布链下交易数据，同时保持共识链的轻量级。
在 kzg-rs 中，我们为 EIP-4844 实现了用于 KZG blob 和批量 blob 验证的纯 Rust crate。kzg-rs 因多种原因而有价值。首先，它是 c-kzg-4844（一种流行的 KZG 实现）的纯 Rust 实现，它利用 C 绑定，从而增强了可审计性和可移植性。此外，kzg-rs 经过优化，可在 SP1 内部运行，目前用于 OP Succinct、Reth Succinct Processor (RSP) 和 Taiko 的汇总实现 中的 blob 验证和 KZG 点评估。
| 指标 | 非预编译版本（周期） | 预编译版本（周期） |
|---|---|---|
| 验证 KZG 证明 | 212,709,402 | 9,391,832 |
| 验证 Blob KZG 证明 | 265,322,934 | 27,960,797 |
| 验证 Blob KZG 证明批处理（10 个证明） | 1,228,277,089 | 270,655,817 |
使用 bls12-381 预编译的极快的以太坊轻客户端
我们采用了 Helios，一个用 Rust 编写的可移植以太坊轻客户端，并将其与 SP1 结合，创建了 SP1-Helios，一个 ZK 以太坊轻客户端，它对于跨链互操作性很有用。
通过我们用于签名验证的优化 bls12-381 预编译，在 SP1 内部验证来自以太坊同步委员会的 512 个签名从 60 亿个周期减少到只有 5000 万个周期。
| 指标 | 非预编译版本（周期） | 预编译版本（周期） |
|---|---|---|
| 总周期数 | 6,732,566,139 | 49,387,331 |
| 验证更新周期 | 3,371,549,554 | 29,968,821 |
| 验证最终确定更新周期 | 3,361,016,585 | 19,418,510 |
revm 中极快的 bn254 配对
我们可以使用我们的 substrate-bn 的直接替代品，它是原始 substrate-bn 的一个分支，来加速 Revm 中的所有 bn254 预编译。我们的 substate-bn 补丁已经合并到我们的许多集成中，包括 op-succinct 和 rsp。通过对 revm 进行 0 行代码更改，我们能够显着加速所有 bn254 EVM 预编译，包括 alt_bn128_pair 运算的 20 倍加速。
| 操作 | 非预编译周期 | 预编译周期 |
|---|---|---|
| alt_bn128_add | 170,298 | 7,616 |
| alt_bn128_mul | 1,860,836 | 141,824 |
| alt_bn128_pair | 155,016,170 | 6,598,690 |
立即加速你的 SP1 程序
程序太慢了？使用 SP1，这是唯一具有 bn254 和 bls12-381 预编译的 zkVM，并亲自体验大幅度的、数量级的速度提升。不要忘记查看我们的其他长长的 预编译 列表，包括 keccak256、sha256、secp256k1 等。请 在此处 与我们联系，如果：
- 你有兴趣创建自己的预编译或想要一个特定的预编译来加速你的程序——我们喜欢与团队合作。
- 你对利用这些预编译的用例感兴趣，例如 kzg 验证、RSP、OP-Succinct、SP1-Helios 等。
代码： 我们的代码是完全开源的，并具有 MIT 许可证：请查看 此处的 SP1，并随时贡献。
附录
预编译的实际作用
下面，我们通过比较原始 Rust 周期数（RISC-V 周期数）与使用预编译的周期数来展示 SP1 中各种椭圆曲线运算的示例。
预编译的实际作用
下面，我们通过比较原始 Rust 周期数（RISC-V 周期数）与使用预编译的周期数来展示 SP1 中各种椭圆曲线运算的示例。
基域 (𝐹ₚ) 运算
| 操作 | 非预编译周期 | 预编译周期 |
|---|---|---|
| 加法 | 402 | 541 |
| 乘法 | 402 | 552 |
| 减法 | 402 | 541 |
| 平方根 | 1,829,272 | 1,647 |
| 反演 | 1,826,741 | 1,599 |
二次扩展域 (𝐹ₚ2) 运算
| 操作 | 非预编译周期 | 预编译周期 |
|---|---|---|
| 加法 | 1,284 | 824 |
| 乘法 | 12,782 | 842 |
| 减法 | 1,588 | 824 |
| 平方根 | 11,481,439 | 6,329,089 |
| 反演 | 1,839,096 | 2,838 |
𝐹ₚ6 运算
| 操作 | 非预编译周期 | 预编译周期 |
|---|---|---|
| 加法 | 3,299 | 1,908 |
| 乘法 | 85,356 | 3,639 |
| 减法 | 4,214 | 1,910 |
| 反演 | 1,979,974 | 10,532 |
𝐹ₚ12 运算
| 操作 | 非预编译周期 | 预编译周期 |
|---|---|---|
| 加法 | 7,211 | 4,440 |
| 乘法 | 272,757 | 12,515 |
| 减法 | 8,062 | 3,459 |
| 反演 | 2,273,149 | 32,516 |
𝐺₁ 射影曲线运算
| 操作 | 非预编译周期 | 预编译周期 |
|---|---|---|
| 射影点加法 | 5,883,275 | 325,849 |
| 射影标量乘法 | 19,569,843 | 2,931,398 |
| 射影点减法 | 7,740,573 | 343,158 |
𝐺₂ 射影曲线运算
| 操作 | 非预编译周期 | 预编译周期 |
|---|---|---|
| 射影点加法 | 40,631,751 | 13,124,100 |
| 射影标量乘法 | 77,193,504 | 1,719,549 |
| 射影点减法 | 29,107,536 | 6,784,692 |
1 | 也称为 bn128 或 alt-bn128
2 | 在幕后，这是一个 RISC-V ecall（即系统调用指令）
- 原文链接： blog.succinct.xyz/succin...
- 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
