诚实验益最大化:理论视角 - 权益证明/区块提议者
- 以太坊中文
- 发布于 2024-10-04 23:59
- 阅读 723
该研究团队提出了一种新的研究方向,即使用图参数来解决诚实验益最大化(Honest MEV)问题,目标是为诚实的矿工找到最大化Gas费用的区块构建方案。他们之前在比特币和Cardano区块链上成功测试了该方法,分别实现了13.4%和55.7%的矿工收入增长。但由于以太坊的特殊性,该团队目前正致力于克服以太坊中存在的交易依赖性、独特的奖励模型和非UTXO模型等挑战。
诚实的 MEV:一个理论视角
问候
大家好!我们是一个研究团队 Togzhan, Soroush, Amir, Sergei,我们关心区块链研究、算法和优化。
TL;DR; (又名摘要)
我们提出了一个新的研究方向:使用图参数来解决诚实 MEV 问题(即诚实的矿工通过最大化 gas 费来形成区块的问题)。该方法已在其他区块链的真实数据上成功测试,在比特币上增加了 13.4% 的矿工收入 (~1 亿美元/年),在 Cardano 上增加了 55.7% 的矿工收入 (~50 万美元/年)。然而,以太坊面临着尚未克服的独特挑战:非平凡的交易依赖性、独特的奖励模型以及导致不可判定的非 UTXO 模型。我们期待社区对我们面临的挑战提出意见和建议。
相关工作
我们之前在其他区块链上的工作:
- 比特币: https://hal.science/hal-03232783v2/file/OptimalMining.pdf
- Cardano: https://hal.science/hal-04616639/file/main.pdf
ethresear.ch 上的类似工作:
该项目
什么是诚实的 MEV? 让我们从一个诚实的验证者的角度来看——一个避免抢跑交易、夹三明治攻击和其他不诚实行为的人。我们验证一个区块所获得的奖励包括基本奖励和交易支付的 gas 费。Gas 费是我们唯一可以影响的变量,所以很自然地,我们有兴趣最大化它们。
我们想做什么? 我们只有一个自由度:如何从交易池中选取一个排序后的交易子集到一个新的区块,以最大化 gas 费。我们的主要目标是使这个决策过程对每个人来说都是最优的、快速的和可访问的。
我不是区块提议者,为什么要关心? 除了对诚实的区块提议者的明显好处外,我们项目的间接影响要大得多:
- 它有助于验证者实现最大的区块利用率
- 它有助于吞吐量,允许更快地将更多交易添加到共识链中
- 收入的增加也激励更多的人成为验证者,从而帮助实现更去中心化的共识。
- 除了协议约束(例如,gas 的动态定价策略)之外,外部约束通常也会影响矿工的决策。例如,矿工可能会选择产生较小的区块以加快区块传播,或者调整算法以管理池中不同的交易集合。该算法的首要目标是允许矿工在约束范围内最大化其盈利能力。这意味着即使矿工必须创建一个小区块,她仍然可以通过选择更好的交易集合来最大化她的收入。
已经做了什么? 如果问题如此根本,一定有人已经做过一些事情了,对吧?没错。 我们的团队一直致力于开发最佳挖矿算法的研究,即为不同的区块链生成具有最大奖励的区块的算法,我们成功地测试、实施和发布了 比特币 和 Cardano 区块链的最佳方法。我们在真实世界的数据上测试了我们的方法,并在比特币上实现了 13.4% 的交易费用增长 (~1 亿美元/年),在 Cardano 上实现了 55.7% 的增长 (~50 万美元/年)。此外,该问题也独立地引起了 其他以太坊研究人员的关注
为什么不直接重用以前的算法? 以太坊的执行模型本质上是复杂的,因为它不遵循 UTXO 模型;最终的gas 费用以及一个交易的 gas 消耗可能取决于其他交易,与其他网络相比,这造成了巨大的易处理性差距。
虽然对于两个交易来说,通过检查一组预定义的规则(如 nonce、余额等)来判断它们是否不冲突很简单,但说一个交易是否干扰了其他交易的 gas 消耗确实很难;如果没有区块 gas 限制,gas 依赖问题在理论上是不可判定的,如果有一个 gas 限制,它是 EXPTIME-complete。
那么你的计划是什么? 我们的计划有几个子目标:
- 找到一种方法来检测池中交易之间的所有依赖关系
- 将问题表述为一个具有图输入的优化实例
- 实现该算法并在真实的池和区块上进行测试
在哪里可以看到更多技术细节? 当然,在接下来的几段中,我们想对我们的框架进行更深入的介绍,以及我们面临的挑战。
交易干扰
交易可能通过三种方式相互影响:它们可能
- 相互依赖,即除非包含另一个交易,否则一个交易不能包含在一个区块中
- 冲突,即不能同时出现在同一个区块中
- gas 依赖,即根据两个交易的同时出现,它们的 gas 费用可能不同
我们将用一个简单的例子来说明所有干扰类型。
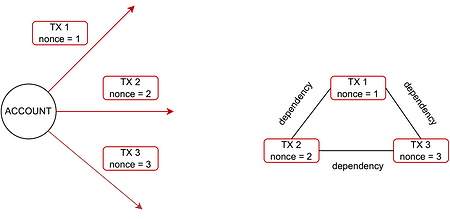
依赖干扰
在一个正确的区块中,来自同一帐户的交易必须具有连续的 nonce,较低的 nonce 必须出现在具有较高 nonce 的交易之前以保持顺序。当矿工观察到交易池时,她应该以保留特定帐户的递增 nonce 顺序的方式选择交易。
此要求创建了依赖关系,在干扰图中捕获为定向依赖边。
冲突干扰
来自同一帐户的交易必须具有连续的 nonce,不允许有两个具有相同 nonce 的交易。当矿工遇到两个具有相同 nonce 的交易时,他必须选择其中一个包含在区块中。
[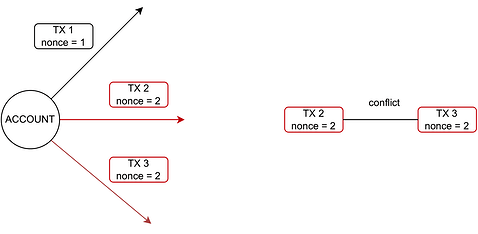 *
1148×562 11.1 KB](https://ethresear.ch/uploads/default/original/3X/5/9/59c90103b23f5e9379b0a6ec8bb378bbd63ee680.png "")
*
1148×562 11.1 KB](https://ethresear.ch/uploads/default/original/3X/5/9/59c90103b23f5e9379b0a6ec8bb378bbd63ee680.png "")
我们向图中引入无向冲突边来表示此限制。
Gas 依赖干扰
最后一个是最复杂的关系,我们将使用一个简单的例子来演示它。考虑一个具有以下两个函数 f 和 g 的智能合约:
function f(): x = 1000
function g(): for i=1 to x { do something }假设 x 最初是 0,并且有两个交易 Tx1 调用 f 和 Tx2 调用 g。如果验证者将 Tx2 放在 Tx1 之前,则 g 中的 for 循环会立即终止,使用非常少的 gas。但是,如果 Tx1 放在 Tx2 之前,则 g 中会使用更多的 gas,从而为验证者带来更高的收入。
DCG 图
我们称 DCG 图为一个图,其中每个顶点表示 mempool 中的一个交易,并且边有三种类型,每种干扰类型一种。
图抽象化是我们框架中的一个重要步骤,因为它将问题分解为两个子任务:从 mempool 构建图和解决图上的优化问题。
图和优化
许多图问题以非常困难而闻名。我们的情况也不例外:仅具有冲突类型边使得选择一个最佳顶点子集作为答案集的问题是 强 NP 难 的。这本质上意味着我们不能期望一个 快速、最佳 且 适用于所有输入 的算法。当我们不能同时拥有这三个时,我们仍然可以选择两个,这就是实践中发生的情况:
- {适用于所有输入,快速,
最佳}:如果我们放弃最佳性,我们会发现自己处于近似和启发式算法的领域。 - {适用于所有输入,
快速, 最佳}:放弃快速的要求导致指数时间算法。虽然它们可能适用于微小的输入,但在真实数据上运行它们是不可行的。 - {
适用于所有输入,快速,最佳}:通常困难的问题在特殊情况下会变得非常容易。例如,树图的三着色问题就很简单。我们声称真实世界的图是结构良好的, 并且可以利用这种结构来构建快速且最佳的算法。
但是,我们没有提供结构良好图的确切定义,有一个 [图类动物园]( https://www.graphclasses.org/)。对于某些图类,通常存在一种专门定制的算法,该算法在给定的类中运行良好(请参阅我们之前的出版物)。我们研究计划的一个步骤是识别真实图所属的最合适的类,并设计一种在该类中运行的算法。
一个例子
我们将用一个例子来演示我们的想法。这里的过度简化是故意的,允许我们展示主要技术,而不会陷入技术细节。
经典的背包问题是[弱 NP 难]( https://en.wikipedia.org/wiki/Weak\_NP-completeness),并且当所有项目体积都是离散的并且每个体积都属于集合[1,…,N]时,存在多项式算法。在这种情况下,存在一种动态规划算法,该算法是多项式的:
- 背包的大小 S
- 最大可能体积 N
考虑一个非常简单的背包问题:所有项目体积都等于 1。当背包的容量为 S 时,我们如何找到一个最佳价值填充?该算法很简单:按价格降序对物品进行排序,然后选择顶部 S 个最有价值的物品。
将其转换为最佳区块挖矿语言,所有交易都支付相等的 1 gas 费用,并且没有冲突或依赖关系,最佳区块将由提供最高小费的交易组成。当没有冲突或依赖关系时,情况就是如此。
当我们添加干扰边时会发生什么?同样,让我们保持简单,并假设我们只有冲突。回到背包公式,对于某些物品对,我们不能将它们打包在一起。
这个问题突然变得非常困难。它不仅是 NP 难的,而且是强 NP 难的。原因是,找到一个[最大独立集]( https://en.wikipedia.org/wiki/Maximal\_independent\_set) 是我们问题的一个特例:通过将背包容量设置为无穷大,并将所有权重设置为 1,找到最佳背包等同于找到一个最大独立集。
虽然很明显并非所有图都可以作为一组交易的冲突图来实现(事实上,依赖图始终是集团的并集),但这与我们的最终目标一致:利用特定的图模式来设计更快的算法。
为了演示如何做到这一点,假设冲突边形成一棵二叉树。到目前为止我们所做的完整假设列表是:
- 每个交易使用 1 单位的 gas
- 我们不对交易可以支付的小费进行限制
- 我们唯一的干扰边类型是冲突边,它们形成一棵二叉树(最不现实的假设)
这个问题从强 NP 难再次变为多项式时间可解!此方法的主要算法技术是动态规划,我们将在一个具体的示例中对其进行演示。
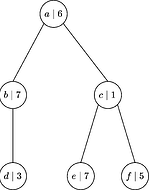
考虑一个由 6 个交易 {a, b, c, d, e, f} 组成的池,具有单位 gas 使用量,矿工小费在下表中给出
| Tx: | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| 总小费: | 6 | 7 | 1 | 3 | 7 | 5 |
| Gas 使用量: | 1 | 1 | 1 | 1 | 1 | 1 |
让我们将区块的大小固定为 3。此外,假设矿工观察到一组冲突,这些冲突形成一个具有边 {(a, b), (a, c), (b,d), (c,e), (c,f)} 的二叉树:
[ *
1259×1600 136 KB](https://ethresear.ch/uploads/default/original/3X/4/7/47e875969aa2f1f1f722a8d61000f2d28b96b284.png "")
*
1259×1600 136 KB](https://ethresear.ch/uploads/default/original/3X/4/7/47e875969aa2f1f1f722a8d61000f2d28b96b284.png "")
引入一个 张量表 opt[tx, IsIncl, Cap],其中 tx ∊ {a, b, c, d, e, f}; IsIncl ∊ {“no”, “yes”} 并且 Cap ∊ {0, 1, 2, 3, 4}。
张量的值定义为:
opt[tx, “no”, c] := “矿工可以获得的最佳收入,仅使用 tx 子树中的交易,当 tx 未包含在内时,如果区块容量为 c”
“yes” 的类似规则:
opt[tx, “yes”, c] := “矿工可以获得的最佳收入,仅使用 tx 子树中的交易,当 tx 包含在内时,如果区块容量为 c”。
现在我们的目标是用值填充此表,然后我们可以找到最大可能的收益,如下所示
max(opt[a, “no”, 3], opt[a, “yes”, 3]),
即,可以使用 a 的子树(即整个集合 {a, b, c, d, e, f})和一个容量为 3 的区块实现的最大利润。
填充策略称为自下而上的动态方法,我们将从树的叶子开始填充表,前进到根。
叶子中的值确定为:
opt[tx, “no”, *] := 0
因为如果我们不采用叶子交易,则强制该包为空
opt[tx, “yes”, 0] := - inf
仅仅是一种约定,将负无穷大利润放入,因为这种配置是不可行的:“yes” 字段强制我们将项目 tx 纳入集合中,但值 0 将区块容量限制为 0。对于叶子表的最后一种情况:
opt[tx, “yes”, ≥ 1] := tip(tx),
因为我们被迫将交易 tx 包含到区块中,并且包含它不会超过区块容量。
对于初始化步骤之后的运行示例,我们将得到:
为了填充内部节点的表,我们将再次考虑两种情况,如果节点被强制包含或不包含“yes”/“no”。让我们从“yes”情况开始,当一个节点 tx 被强制包含到区块中时。节点 tx 最多有两个子节点,假设它正好有两个子节点 tx_l 和 tx_r(可以通过引入一个具有单位 gas 使用量和零小费的虚拟节点来处理一个子节点的情况)。
然后,为了找到 opt[tx, “yes”, c] 的值,首先我们需要分配一个单位的容量给交易 tx,剩余的容量在两个子树之间分配。请注意,如果我们采用 tx,那么由于 tx 的冲突边,我们不能采用 tx_l 或 tx_r 到区块。因此
opt[tx, “yes”, c] := tip(tx) +
max (opt[tx_l, “no”, i] + opt[tx_r, “no”, c - i - 1])
for i in [0, c)
i 表示分配给左子节点的容量,所有剩余容量分配给右子节点。
类似的推理使我们得出“no”情况的公式:
opt[tx, “no”, c] := max(
max{opt[tx_l, “no”, i], opt[tx_l, “yes”, i}
+ max{opt[tx_r, “no”, c - i - 1], opt[tx_r, “no”, c - i - 1]})
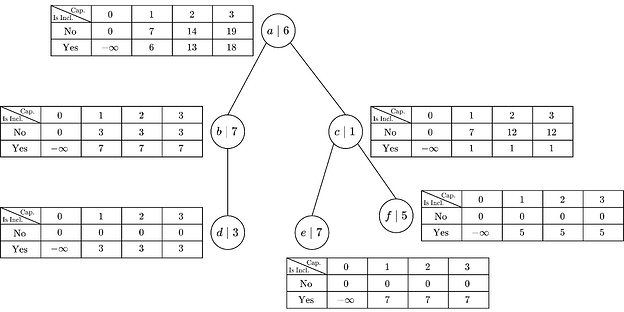
其中必须有 max{opt[tx_l, “no”/“yes”, *]} 是因为需要考虑是否将子节点包含在集合中或排除在集合之外的两种情况。使用这些公式填充表格,我们最终得到:
[ *
1600×801 41.1 KB](https://ethresear.ch/uploads/default/original/3X/2/4/2461dd155e6cb079d8ae3afe3642efd3840b0742.png "")
*
1600×801 41.1 KB](https://ethresear.ch/uploads/default/original/3X/2/4/2461dd155e6cb079d8ae3afe3642efd3840b0742.png "")
我们可以看到,大小为 3 的最佳区块将从根目录中的表格中产生 19 的收入,这是区块 {b, e, f} 的情况。不仅找到答案,而且找到区块本身是通过一种标准技术实现的,即在评估内部节点的公式时,保持子节点之间的最佳容量分配,并保持是否将子节点放入集合中的最佳决策。
尽管我们做了过多的简化,但我们针对其他区块链的通用算法具有相同的风格:我们找到一种方法,使用简单的组合操作(在本例中是将两个子树组合到节点的树中)从基本部分(本例中的叶子)开始构建图,并在组合操作期间提供重新计算目标函数的方法。
挑战
我们确定了项目期间需要解决的挑战。这些挑战本质上各不相同:有些与工程和计算有关,而另一些则纯粹是理论性的。
我们预计会面临以下挑战:
- 拥有一个连接良好的节点来访问交易池。
- 能够执行交易捆绑包并获得其gas使用情况。
- 如果我们执行每个可能的交易子集并以每种可能的顺序执行,那么能够确定两个交易是否完全gas依赖是可能的。一种方法是使用各种工具,包括符号执行工具和静态分析工具。
- 检查交易干扰图的结构,从图类动物园中选择最接近的类,并创建一个有效的算法来解决优化问题
意见征询
我们真诚地相信,有可能获得以太坊交易收入的增长,并击败现实世界的矿工结果。如果我们这样做,将极大地造福于矿工和以太坊生态系统。你对此项目有何看法?请随时分享你的意见和潜在的担忧。让我们在下面进行讨论!
- 原文链接: ethresear.ch/t/honest-me...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- Solana的区块构建之战 57 浏览
- 如何去中心化构建区块? 158 浏览
- CoW DAO月度回顾:2026年1月 - CoW DAO 310 浏览
- Hegató Headliner 提案:FOCIL,EIP-7805 - 魔术师 / 原始汤 368 浏览
- Hegotá 头条提案:FOCIL,EIP-7805 - 魔法师 / 原始汤 303 浏览
- Hegató Headliner 提案:FOCIL,EIP-7805 - 魔法师/原始汤 375 浏览
- Hegotá Headliner 提案:FOCIL,EIP-7805 - 魔术师 / 原始汤 358 浏览
- Hegotá Headliner 提案:FOCIL, EIP-7805 - 魔法师 / 原始汤 295 浏览
- Hegotá 主题提案:FOCIL,EIP-7805 - 魔法师 / 原始汤 339 浏览
- Hegotá 主题提案:FOCIL,EIP-7805 - 魔术师 / 原始汤 432 浏览
- Hegotá Headliner 提案:FOCIL,EIP-7805 - 魔法师 / 原始汤 602 浏览
- Uniswap V4 Hooks — Hooks介绍 — 找到你的问题的答案 356 浏览
 \
1148×562 15.8 KB
\
1148×562 15.8 KB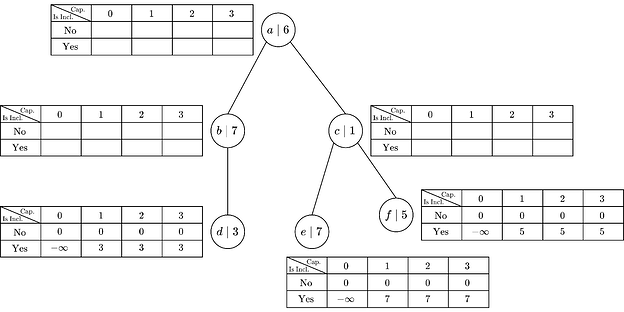 \
1600×801 37.3 KB
\
1600×801 37.3 KB
