区块链中的数学 - BLS门限签名

写在前面

本文接着前一篇BLS密钥聚合，讲下原始的聚合密钥签名可能出现的问题，需要一些背景知识铺垫，以Schnorr签名为例来说明，对此不熟悉的可先参考相关文章：Schnorr签名与椭圆曲线 和Schnorr密钥聚合

密钥消除攻击

在Schnorr密钥聚合一文中，是最简单的聚合方式，现在可以进一步说下了。
这种方式的前提是要求参与者都是诚实的，实际实现中要加入额外的公钥验证，否则会出现安全问题。
下面说下可能的安全问题：
假设有两个参与者A和B，$P_A,P_B$分别是二者的公钥。
假设B不诚实，参与密钥聚合过程中，提供假的公钥$P_{FB}=P_B-P_A$, 导致聚合公钥：
$P=P_A+P_{FB}=P_A+P_B-P_A=P_B$ ，

这样就控制了聚合公钥成为自己的公钥，从而只用B自己的签名来覆盖A的签名，本来需要A，B共同签名的交易，现在只要B单独签名（伪造聚合签名）就可以了。
这种攻击可称为“密钥消除攻击”，亦属于“Rogue Key Attacks”。

简单的解决方案是在密钥聚合操作中，参与者提供公钥所有权证明，即签署任意消息，但这会增加交互过程，如果这个所有权证明也放到区块链上，增加存储大小。
成熟的解决方案类似BLS密钥聚合文中第二种方案。
结合Schnorr简记如下：

1. 参与者公钥hash聚合 $L = H(P_A+P_B）$
2. 生成聚合公钥 $P =H(L,P_A)*P_A+H(L,P_B)*P_B$
3. 生成聚合随机数 $R =R_A+R_B$
4. 生成聚合签名
   
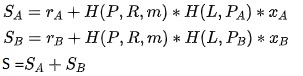
5. (R, S)即最后得到的签名，验证如下：
   S * G = R + H(P, R, m) * P

易见，可以推广到多个参与者，如果恶意参与者采用上文所说的密钥消除攻击，本方案中就产生不了有效的签名。
接下来继续回到BLS系列

BLS m of n门限签名

BLS 使用了不同方法实现门限签名，以 2-3 多重签名为例说明（可扩展为任意的 m-n 多重签名）。

准备阶段：

用 i = 1,2,3 表示多签所有参与者集合，按照惯例，$x_i$表示私钥，$P_i=x_i \times G$ 表示公钥。计算聚合公钥：

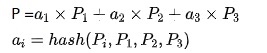
现在，每个参与者本地对i签名，以证明该i是聚合公钥中的一员。
记$q_i$为(P, i)哈希映射到曲线上的点，参与者i将签名聚合后得到：

$MK_i=(a_1 * x_1) * q_i + (a_2 * x_2) * q_i+ (a_3 * x_3) * q_i$

这个签名被称作“成员密钥”，每个成员密钥都是所有参与者对消息$q_i$的 n-n 多重签名，即：

$e(G,MK_i)=e(P,q_i)$

因为：

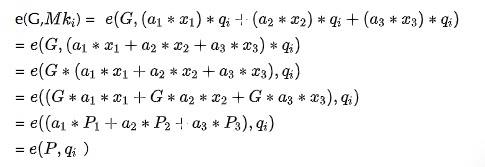
签名阶段：

假设只用私钥$x_1$ 和 $x_3$给交易签名，我们会生成 2 个签名$S_1$ 和 $S_3$：

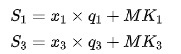
二者相加，聚合成单一的签名和公钥：
$(S’, P’) =(S_1 + S_3 , P_1 + P_3)$

验证阶段：

为了验证 2-3多重签名，需证明如下等式成立：

$e(G, S’) =e(P',H(p,m)) * e(P,q_1 + q_3)$

记(P, m)哈希映射到曲线上的点为, 结合成员密钥$MK_1$ 和$MK_3$ 是对消息 $q_1$和$q_3$的签名，可得：

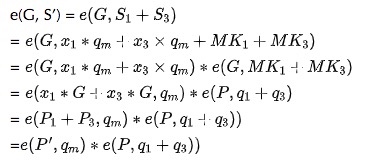
注：有的文章将$q_i$记为H(P, i)代表映射到曲线的点，个人认为不大恰当，H(P, i)很容易被理解成一个哈希结果的标量值，而不是有向的点，造成理解上的不便！

小结

本文主要参考：
https://bitcointechtalk.com/scaling-bitcoin-schnorr-signatures-abe3b5c275d1

最近几篇的思路大致为：BLS签名介绍 --> 密钥聚合 --> BLS门限签名 -->BLS基石（双线性函数）和配对

下一篇继续介绍双线性映射函数！

欢迎关注公众号：blocksight

相关阅读：

区块链中的数学-BLS密钥聚合 BLS密钥聚合

区块链中的数学 - BLS数字签名 BLS签名及验证

区块链中的数学 - 参与者 < 门限值t的密钥更新Amir Herzberg方案 Amir Herzberg改进方案

区块链中的数学 - Feldman的可验证的密钥分享 Feldman可验证密钥分享方案

区块链中的数学 - Ed25519签名 Ed25519签名

区块链中的数学-ElGamal算法 ElGamal算法签名及验证&实例演练

区块链中的数学-VRF基于ECC公钥体制的证明验证过程 基于椭圆曲线的VRF证明验证过程

Schorr签名与椭圆曲线 Schorr签名与椭圆曲线

区块链中的数学-Uniwap自动化做市商核心算法解析 Uniwap核心算法解析（中）