以太坊质押市场正式框架的关键见解 - 经济学
- 以太坊中文
- 发布于 2025-07-26 17:58
- 阅读 1033
该文章研究了以太坊发行曲线变化对不同类型质押者决策的影响,通过博弈论模型分析了不同发行计划对质押市场去中心化的影响。研究发现,降低发行量可能加剧竞争,降低solo staker的市场份额,增加中心化质押解决方案的市场份额。此外,模型预测solo staking的盈利能力会降低,可能威胁其长期可行性。
这篇文章总结了密码经济学中心的研究。请在此处查看完整报告这里。这项研究由cyber.Fund资助。这篇文章中表达的观点仅代表作者Juan Beccuti、Thunj Chantramonklasri、Matthias Hafner和Nicolas Oderbolz。我们感谢@artofkot、@kkulk、@PaulYa5hin和@thelazyliz的宝贵支持、评论和审查。
概括
为了研究以太坊发行曲线的变化如何影响不同类别质押者的质押决策,并因此影响质押市场的去中心化程度,我们开发了一个以太坊质押市场的博弈论模型,并用它来对不同的发行计划进行比较分析。我们将此分析的结果放在现有的经验文献以及我们自己对质押供给弹性的初步估计的背景下进行讨论。除了为减少协议发行量的辩论做出贡献外,我们希望该模型可以作为进一步扩展的基础,为分析不同协议变更下的质押动态提供一个灵活的框架。
现有的经验研究,以及我们自己使用工具变量(IV)方法进行的估计,都倾向于表明,与其它质押类别相比,单人质押者可能对质押收益的变化更为敏感。
下面介绍的博弈论模型表明,质押者的均衡质押供给由其质押成本和收入以及其它市场参与者的战略行为决定。我们的结果表明,后期的竞争市场力量可能在解释为什么单人质押者对质押收益的变化更为敏感方面发挥重要作用。其它质押类别受益于额外的收入来源,例如卓越的 MEV 访问权限和 DeFi 收益,这使得他们对共识奖励的变化不太敏感。鉴于以太坊的向下倾斜发行计划,具有战略眼光的单人质押者会将这些竞争压力内在化,从而使他们对共识收益的变化更加敏感。
通过比较当前发行计划下和拟议的替代方案下我们模型的均衡,我们发现减少发行量可能会加剧这种影响。虽然我们模型中发行计划的改变与所有质押类别的质押 ETH 供应量的减少有关,但它也与单人质押者市场份额的减少和中心化质押解决方案市场份额的增加有关。
此外,我们的模型预测单人质押的盈利能力不如其它质押方式。虽然这超出了我们模型的范围,但这可能会削弱单人质押的长期可行性,并加速单人质押者退出市场,转而选择替代解决方案,例如去中心化质押服务提供商和流动性质押。
动机
过去几年中,以太坊权益证明 (PoS) 协议中质押的 ETH 总量显着增长,围绕当前发行计划长期可持续性的讨论已变得突出。这场辩论的核心是在验证器基础设施的有效利用、发行驱动的通货膨胀和经济安全之间的权衡。
人们认为,减少共识发行计划对于避免大多数 ETH 流通供应量被质押的最终局面非常重要(例如,参见 Elowsson (2024) 和 Schwarz-Schilling (2024))。这种结果意味着质押的 ETH 供应量远远超过了经济安全所需的阈值,导致不必要的通胀压力和验证器资源的低效分配。此外,人们还担心流动性质押代币的激增及其取代 ETH 成为生态系统中事实上的货币的潜力所带来的潜在系统性风险。这些考虑因素表明,修改发行计划以有效减少质押激励可能是审慎的。
相反,与中心化解决方案相比,减少质押奖励可能会不成比例地影响相对昂贵的去中心化质押解决方案的盈利能力,从而可能导致更少的去中心化。特别是,已经只占验证器总数一小部分的单人质押者可能会不成比例地被挤出市场。
在下文中,我们旨在通过检查不同的质押方法,特别是单人质押者,如何受到以太坊共识发行政策变化的不同影响,来测试这种论点的有效性。具体来说,我们专注于回答两个关键的研究问题:
- 不同类型的质押者如何应对发行计划的变化?
- 这些变化可能如何影响以太坊质押生态系统的去中心化?
方法论
为了解决这些研究问题,我们采用了以下方法论,我们在本文中重点介绍了其结果:
- 实证估计: 我们使用工具变量方法来估计质押奖励的变化如何影响这些不同质押类别中质押 ETH 的供应量。
- 博弈论模型: 在实证结果的指导下,我们开发了一个以太坊质押市场的博弈论模型,在该模型中,不同类型的质押代理根据与不同质押方法相关的收入来源和成本结构来确定其质押供应量。目标是构建一个建模框架,将个人质押决策与以太坊质押市场的总体质押供应量联系起来。
- 模拟和比较分析: 通过在各种参数配置下模拟这个博弈论模型,我们试图了解个体成本结构和收入来源如何影响总体质押市场中的均衡结果。此外,我们将模型校准到特定的参数设置,并评估以太坊发行计划的变化如何影响质押市场的结果,特别是不同质押类别的市场份额。
质押供给弹性估计
方法论
我们估计了不同质押者类型的质押供给对质押奖励变化的敏感度。为了解决内生性问题,我们采用工具变量(IV)方法。内生性在这种情况下是一个问题,因为在理论上,在给定时间点观察到的质押收益和质押供应的任何组合都是市场均衡的结果,其中质押的供应和需求相遇。这种市场均衡的变化可能源于供应曲线的移动和需求曲线的移动,从而在对质押收益和质押供应之间的相关性的任何简单估计中产生内生性。因此,这种估计方法的目的是识别在不影响决定供应曲线的因素的同时,改变质押 ETH 需求曲线的工具。使用此类工具使我们能够至少在局部均衡点隔离供应曲线的形状。
对于不同质押类别的供应收益弹性估计,我们建议使用 gas 费用作为可靠的工具。Gas 费用可能代表这种情况下的有效工具,因为它们直接影响质押奖励,但与质押供应的决定因素保持外生性,因为它们受到网络活动、DeFi 交易和 NFT 交易等外部因素的驱动。利用自然波动和公开可用的 gas 费用数据,我们使用日级数据进行两阶段最小二乘法 (2SLS) 分析,其中奖励和质押金额以美元计价。此处提供了对估计方法和相应结果的详细说明这里。
结果
重要的是,该方法产生的供应收益弹性估计表明,与所有质押者的质押供应相比,单人质押者的质押供应对质押收益的变化更为敏感。对于单人质押者,质押供应对质押奖励的弹性估计为 1.184,对于所有质押者,弹性估计为 1.078。这两个估计值在 1% 的水平上都具有统计学意义。这些结果与 Eloranta 和 Helminen (2025) 的发现总体一致,他们的估计同样表明,与所有质押者相比,单人质押者对质押收益的变化更为敏感。
表 1:使用 gas 费用作为质押奖励工具的 2SLS 估计
| 单人质押 | 所有质押类型 | |||
|---|---|---|---|---|
| (1) <br> 对数金额 <br> 质押 (美元) | (2) <br> 对数金额 <br> 质押 (美元) | (3) <br> 对数金额 <br> 质押 (美元) | (4) <br> 对数金额 <br> 质押 (美元) | |
| --- | --- | --- | --- | --- |
| 对数奖励 (美元)t | 1.184\*\*\*<br>(0.073) | | 1.078\*\*\*<br>(0.035) | | | 对数奖励 (美元)t−1 | | 1.176\*\*\*<br>(0.074) | | 1.075\*\*\*<br>(0.036) | | 常数 | 6.774**<br>(0.877) | 6.868\*\*\*<br>(0.888) | 7.739\*\*\*<br>(0.543) | 7.786\*\*\*<br>(0.556) | | 观察 | 622 | 621 | 622 | 621 | | R 平方 | 0.128 | 0.101 | 0.858 | 0.851 | | 注意: 此表中报告的系数可以解释为质押供应的收益弹性。这些系数报告了与同一时期或滞后一周的质押奖励的美元价值增加 1% 相关的质押 ETH 金额(以美元计价)的估计百分比增加。第 1 列和第 2 列报告了在单人质押者样本上估计的结果。第 3 列和第 4 列报告了在所有质押样本上估计的结果。括号中报告了稳健的标准误差。 | | \*\*\* p<0.01, \*\* p<0.05, \* p<0.1 |
博弈论模型
为了进一步了解是什么驱动了质押供应弹性,我们开发了一个博弈论框架,使我们能够将不同质押市场参与者的战略质押决策建模为以太坊发行计划、其它外部收入来源和质押成本的函数。
代理类型
我们提出了一个分段质押市场的博弈论模型,其中 ETH 持有者根据他们的偏好和/或技术复杂程度进行区分,这反过来决定了他们将如何质押。具体来说,考虑了三种不同的 ETH 持有者类型:
\theta \in \{\text{零售商, 技术人员, 专家}\}
θ∈{Retailer, Techie, Expert}
每个类别包含固定数量的质押者,分别表示为 N_rNr、N_tNt 和 N_{ss}Nss,分别对应零售商、技术人员和专家(或单人质押者)。为了确保易处理性,假设组内同质性。
分段质押市场
此外,该模型还包含几种质押方法,这些方法在 ETH 持有者承担的成本及其提供的收入来源方面有所不同。这些方法包括单人质押、通过中心化服务提供商 (cSSP) 进行质押,例如中心化交易所或专业的直接质押委托公司(如 Kiln),以及通过去中心化服务提供商 (dSSP) 进行质押,该提供商通过 LST 提供额外的 DeFi 收益,例如 Lido。我们没有明确地对再质押进行建模。
每种类型的 ETH 持有者根据其专业水平具有不同的质押选项。原则上,零售商专门通过中心化质押服务提供商 (cSSP) 进行质押;技术人员在 cSSP 和去中心化提供商 (dSSP) 之间进行选择;专家可以访问所有选项,包括单人质押。
然而,我们对收入、成本和偏好进行建模,从而形成一个分段质押市场。也就是说,每个 ETH 持有者选择一种质押方法或退出,并且不会跨选项进行多元化。具体来说:
- 零售商要么使用 cSSP 进行质押,要么弃权,这反映了对易用性和有限技术能力的需求。
- 技术人员更喜欢 dSSP 而不是 cSSP,因为他们从 LST 中获得更高的回报。也就是说,我们对收入和成本函数进行建模,使技术人员的利润大于零售商的利润。
- 专家被假定为专门选择单人质押——尽管利润可能较低——因为他们从为去中心化做出贡献中获得内在的(但未建模的)效用。因此,专家进行单人质押或退出质押市场。
请注意,其它研究也考虑了分段质押市场,例如 Kotelskiy 等人 (2024)。另请注意,我们没有将质押决策建模为投资组合分配问题。相反,每个 ETH 持有者将其全部质押分配给为其类型产生最高效用的选项。该框架强调清晰的分割,而不是混合策略。另一种方法可能涉及投资组合管理。在这种情况下,下面介绍的模型需要进行修改以避免角点解——例如,通过明确纳入专家对去中心化的内在偏好。
质押收入
根据他们选择的质押选项,ETH 持有者可以从三个不同的来源获得收入:1) 共识层收入,2) MEV 收入,以及 3) 额外的 DeFi 收益。
第一个是共识层收入,由协议的发行计划决定。质押时提供给 ETH 持有者 ii 的年度共识收益表示为 y_i(D)yi(D)。在当前的发行计划下,年度共识收益由下式给出
y_i(D) = \frac{cF}{\sqrt{D}} = \frac{2.6 \cdot 64}{\sqrt{D}},
yi(D)=cF√D=2.6⋅64√D,
其中 DD 表示协议中质押的 ETH 总量。在后面的章节中,我们将比较当前发行计划 y_i(D)yi(D) 和备选规范 y_i'(D)y′i(D) 下的模型结果。
第二个收入来源是 MEV 收入。被选为区块生产中的提议者的验证者可以通过构建交易提取额外的收入,以下称为 MEV 收入。假设 N = D/32N=D/32 表示验证者的总数,控制 d_i/32di/32 个验证者的 ETH 持有者被选为提议者的概率为 d_i/Ddi/D。相反,如果质押者加入质押池(即通过中介进行质押),提议者可以将 MEV 收入与池中的其他人分享。池中任何验证者被选为提议者的概率为 d_{pool}/Ddpool/D,并且质押 d_idi 的验证者获得 d_i/d_{pool}di/dpool 的份额。因此,池中质押者的预期 MEV 收入与单人质押者相同。在这两种情况下,ETH 持有者的预期年度 MEV 收入 y_vyv 在理论上由下式给出
y_v \cdot \frac{d_i}{D}.
yv⋅diD.
第三个收入来源是额外的 DeFi 收益。使用 dSSP 的 ETH 持有者可以通过再投资他们收到的 LST 来获得额外的收益。来自此收入来源的年度收益简单地定义为 y_dyd。
质押成本
从 ETH 持有者的角度来看,质押与不同的成本相关。在本模型中,允许 ETH 持有者面临的成本函数对每个质押解决方案有所不同。我们定义一个包含固定成本和非线性可变成本的成本函数
C(d) = C+c\,d^{\alpha}.
C(d)=C+cdα.
稍后,我们将校准模型,寻找一组参数,该参数集给出的质押供应分布与本研究时市场中观察到的分布相似。我们还假设成本函数是这样的,即存在内部解。这种假设在代理对其选择没有约束性约束(例如预算约束)的模型中很常见。
此外,通过中介进行质押的 ETH 持有者会产生费用,费用被建模为对收入的税收,因此与成本函数分开处理。cSSP 费率表示为 f_cfc,dSSP 费率表示为 f_dfd,两者都在基线模型中被假定为外生变量。因此,费用被简单地假定为固定费用,而不是由市场中质押服务提供商的战略行为决定的。后续的扩展将放宽这一假设,并在一定程度上允许将费用确定为模型中质押服务提供商的利润最大化问题的函数。
质押决策
在 ETH 价格恒定的假设下,从而将质押决策与价格波动和通货膨胀效应隔离开来,每个质押者都会最大化预期年度利润。
给定其它质押者的存款 \{d_{ss},d_r,d_t\}{dss,dr,dt},一个具有代表性的专家选择一个存款 \hat{d}_{ss}\geq 0^dss≥0 来最大化
\max_{\hat{d}_{ss}}\, \Big\{ y_i(D)\,\hat{d}_{ss} + y_v\, P_{ss}(D) - \Big(C_{ss}+c_{ss}\,\hat{d}_{e}^{\alpha_{ss}}\Big) \Big\},
max^dss{yi(D)^dss+yvPss(D)−(Css+css^dαsse)},
其中
P_{ss}(D)=\frac{\hat{d}_{ss}}{\hat{d}_{ss}+(N_{ss}-1)d_{ss}+N_r d_r+N_t d_t},
Pss(D)=^dss^dss+(Nss−1)dss+Nrdr+Ntdt,
并且其利润不为负(负利润意味着没有质押)。
让 P_{ss}(D)Pss(D) 表示存款为 \hat{d}_{ss}^dss 的质押者成为提议者的概率。我们将此概率建模为质押者的存款与总存款的比率,如分母所示。但是,更准确的表示方法会将其建模为质押者控制的验证者数量与验证者总数的比率。这将需要一个步进函数,该函数每增加 32 ETH 就会递增,对应于验证器激活阈值。为了便于处理,我们改为将 P_{ss}Pss 建模为 \hat{d}_{ss}^dss 的连续函数,这简化了分析。
\hat{d}_{ss}^*^d∗ss 表示最大化问题的最佳选择。由于每个质押者类型类别内的同质性,所有专家必须在均衡中选择相同的存款水平。也就是说,在均衡中,个体最佳选择 \hat{d}_{ss}^*^d∗ss 满足 \hat{d}_{ss}^* = d_{ss}^d∗ss=dss。
类似地,每个技术人员选择一个存款 \hat{d}_{t}\geq 0^dt≥0 来最大化
\max_{\hat{d}_{t}}\, \Big\{ (1-f_d)\Big[y_i(D)\,\hat{d}_t + y_v\, P_t(D)\Big] + y_d\, \hat{d}_t - \Big(C_{t}+c_{t}\,\hat{d}_t^{\alpha_{t}}\Big) \Big\},
max^dt{(1−fd)[yi(D)^dt+yvPt(D)]+yd^dt−(Ct+ct^dαtt)},
其中
P_t(D)=\frac{\hat{d}_{t}}{N_{ss}\,d_{ss}+\hat{d}_t+(N_t-1)d_t+N_r d_r}.
Pt(D)=^dtNssdss+^dt+(Nt−1)dt+Nrdr.
同质性再次意味着 \hat{d}_t^*=d_t^d∗t=dt。请注意,这种类型的质押者支付费用 f_dfd 并享受 DeFi 收益 y_dyd。
零售商选择一个存款 \hat{d}_{r}\geq 0^dr≥0 来最大化
\max_{\hat{d}_{r}}\, \Big\{ (1-f_c)\Big[y_i(D)\,\hat{d}_r + y_v\, P_r(D)\Big] - \Big(C_{r}+c_{r}\,\hat{d}_r^{\alpha_{r}}\Big) \Big\},
max^dr{(1−fc)[yi(D)^dr+yvPr(D)]−(Cr+cr^dαrr)},
其中
P_r(D)=\frac{\hat{d}_{r}}{N_{ss}\,d_{ss}+N_t\,d_t+\hat{d}_r+(N_r-1)d_r}.
Pr(D)=^drNssdss+Ntdt+^dr+(Nr−1)dr.
同样,同质性意味着 \hat{d}_r^*=d_r^d∗r=dr。
根据他们的类型,这些 ETH 持有者会就质押多少 ETH 做出战略决策。实际上,他们会考虑到他们的成本和要支付的费用,以及他们对其它代理的质押行为的预期,来选择其利润最大化的质押 ETH 供应量。完整论文提供了该模型的详细说明以及由此产生的纳什均衡的推导。
以上质押决策定义了基线模型中不同代理类型的战略行为。然而,现实世界的质押受到额外的复杂性的影响,我们现在将其作为模型扩展引入。
模型扩展
我们以几种关键方式扩展了基线模型,向质押代理的特征和中介市场添加了重要的细节(有关这些扩展的正式说明,请参阅完整报告):
- 单人质押者的 MEV 奖励的可变性: 我们假设质押类型专家具有风险厌恶性,并且会因 MEV 收入的方差而感到效用降低。其它质押者类型的利润最大化问题保持不变。这种公式考虑了这样一个事实,即单人质押者可能需要数年时间才能提出具有高 MEV 的区块,而池中的其它质押者可以从随着时间的推移平滑 MEV 收入中受益。
- 非策略性质押者类型: 我们将零售商类别分为两个子组:(1) 机构和 (2) 不关注的散户投资者。后一组被假定为对发行收益的变化没有反应,这意味着他们不会采取策略性行为。此行为可能源于他们的无弹性,但更现实的解释是他们是不关注的代理,或者他们的利润最大化决策会导致角点解(质押全部或不质押)。将这种类型的代理纳入模型的首要目的是评估它们的存在如何影响其它类型的质押行为,特别是单人质押者。
- 具有市场力量的中介 SSP: 最后,我们通过纳入具有市场力量的中介 dSSP,增加了质押提供商的中介市场的复杂性。在基线模型中,假定质押费用是固定的,因此 dSSP 在完全竞争下运营,并且它们本身提供质押服务。更现实的方法是将 dSSP 建模为质押者和中心化质押服务提供商 (cSSP) 之间的中介或中间件。例如,当 ETH 持有者决定使用 Lido 进行质押时,质押是通过 cSSP 进行管理的。Lido 本身并不直接提供质押服务;相反,它促进了 ETH 持有者和 cSSP 之间的连接。在此安排中,ETH 持有者通过收到代表其质押的衍生品而从 Lido 中受益。下图以简化的形式说明了此设置。
图 1:dSSP 作为中间件的市场结构
结果
为了评估不同的发行计划如何影响均衡质押决策,我们比较了两种备选发行规则下的质押结果。第一个发行计划对应于以太坊协议当前实施的发行计划:
y_i(D) = \frac{2.6 \cdot 64}{\sqrt{D}},
yi(D)=2.6⋅64√D,
其中 DD 表示质押存款水平。第二个发行计划遵循 Elowsson (2024) 提出的备选提案之一:
y'_i(D) = \frac{2.6\cdot 64}{\sqrt{D} \cdot (1+k\cdot D)},
y′i(D)=2.6⋅64√D⋅(1+k⋅D),
其中 k=2^{-25}k=2−25,DD 再次表示质押的 ETH 总量。
这些计划可能会以不同的方式影响质押激励。在比较均衡质押决策之前,我们首先进行数值模拟,以更好地了解从 y_i(D)yi(D) 过渡到 y'_i(D)y′i(D) 的影响背后的力量。
数值模拟
我们对基线模型进行了广泛的模拟,在 1000 万次运行中随机改变所有参数。这些模拟提供了对不同参数如何在从 y_i(D)yi(D) 移动到 y'_i(D)y′i(D) 时影响均衡调整的洞察。
我们的主要发现如下:
- 观察 1: 当从 y_i(D)yi(D) 过渡到 y'_i(D)y′i(D) 时,更高的边际成本会导致均衡质押供应的调整幅度更小。图 2a - 2c 使用单人质押作为示例说明了这种效果。
- 观察 2: 额外的 MEV 收入或 DeFi 收益的存在会抑制质押者对发行计划变化的响应。图 2d 和 2e 使用通过 dSSP 进行质押作为示例说明了这种效果。
- 观察 3: 不同代理类型对发行计划变化的敏感性是相互依存的。例如,当技术人员对发行计划变化的敏感性降低时(例如,当额外的 DeFi 收益很高时),专家对发行计划变化的敏感性会增加。图 2f 说明了这种效果。
图 2:成本参数与均衡质押决策变化之间的关系
注意: 这些图显示了当从 y_i(D)yi(D) 过渡到 y'_i(D)y′i(D) 时,不同质押方法的总质押供应的平均百分比变化(按模型参数的不同级别分类)。箱的数量设置为 20。
这些模拟提供了初步的见解,但有必要对不同发行计划下的均衡结果进行结构化的比较。我们现在转到包含其它模型改进的比较分析。
模型校准
我们使用特定参数校准模型,并比较两种发行计划下的纳什均衡。鉴于需要校准的参数数量,我们发现基于模拟力矩的方法(即,以算法方式设置参数以最小化模拟市场份额和观察到的市场份额之间的距离)估计模型参数无法提供稳定的最佳拟合。换句话说,我们发现各种可能的参数组合都可以产生与观察到的数据一致的模拟市场份额(有关更多详细信息,请参阅完整报告)。
作为第二好的方法,我们提出了与我们对以太坊质押市场的定性理解一致的参数设置,并且在基线模型中实现了与表 2 中报告的不同质押类型的观察到的市场份额的紧密拟合。为了形成我们的定性理解,我们为 Reddit 论坛 r/ethstaker 上的单人质押者进行了一项调查。
表 2:参数校准中使用的参考质押分布
| 质押方法 | M ETH | % |
|---|---|---|
| dSSP | 18 | 54.1% |
| cSSP | 14.4 | 44.6% |
| 单人质押 | 0.9 | 2.7% |
| 总计 | 34.2 |
注意: 验证者的估计数量基于对 Kotelskiy 等人 (2024) 报告的分类的简化,并计算为质押的 ETH 数量除以 32。我们将 DSM、LRT、鲸鱼和未识别分类为 dSSP。同时,cSSP 由 CSP 和 CeX 组成。
重要的是,我们假设单人质押会产生固定成本,而通过 dSSP 或 cSSP 进行质押则不会:
C_{ss} = 0.4,\quad C_{t} = 0,\quad C_{r} = 0.
Css=0.4,Ct=0,Cr=0. 与通过中介进行质押相反,单独质押需要个人设置一个运行共识和执行客户端的以太坊节点。为此,单独质押者可以购买专用硬件、订阅云计算服务或使用现有硬件。与这些选项相关的成本差异很大。更复杂的是,可以使用一系列硬件规范来运行节点,每种规范的成本各不相同。迄今为止,文献对单独验证者的硬件成本做出了高度简化的假设。特别是,pa7x1 (2024) 和 Kotelskiy et al. (2024) 都假设单独质押者会预留 1000 美元来初步购买必要的硬件,并在 5 年的时间内摊销。从 r/ethstaker 上的调查中收集到的轶事证据通常支持这一假设,但也揭示了相当大的差异,因为一些质押者使用现有硬件,并且不购买专用硬件进行质押。
与硬件成本类似,我们假设能源和互联网的成本是固定的,因为它们是运行以太坊节点的基本要求,但当向节点添加额外的验证者时,成本不会增加。同样,pa7x1 (2024) 和 Kotelskiy et al. (2024) 假设每周的能源成本约为 1.4 至 2 美元,互联网成本约为每周 0 至 12 美元。这些假设通常得到 r/ethstaker 调查中轶事证据的支持。但是,可能存在很大的差异,因为很难假设业余单独质押者会明确监控并根据其单独质押设置的互联网和能源消耗来做出质押决策。
总而言之,我们假设固定成本约为 \approx 1'000 \$/year≈1′000$/year。这包括通常假设在 55 年内摊销的硬件(200-400200−400\$/year$/year)、高速稳定的互联网连接(5050\$/month$/month)和其他电力支出(100100\$/year$/year)。以 ETH 表示此成本,以 2'400 美元的 ETH 价格计算,我们得到 C_{ss} = 0.4Css=0.4 的参数设置。同样,我们假设通过中介进行质押不会从 ETH 持有者的角度产生任何固定成本。因此,我们将 C_{r} = 0Cr=0 和 C_{r} = 0Cr=0 设置为 0。
我们进一步假设
c\_{ss} < c\_{t} < c\_{r} \\quad \\text{and} \\quad \\alpha\_{ss} > \\alpha\_{t},\ \\alpha\_{ss} > \\alpha\_{r},\ \\alpha\_{t} = \\alpha\_{r}.css<ct<crandαss>αt,αss>αr,αt=αr.
关于各种质押方法的可变成本的文献要少得多。因此,我们主要依赖于轶事证据和简化的假设。我们认为,在考虑单独质押的维护成本时,施加上述条件可能是合理的。随着验证者数量的增加,复杂性和运营管理费用可能会非线性地增加。例如,更多的验证者需要更好的网络管理。管理和更新多个节点,以及处理安全补丁和升级,需要更多的精力,因为基础设施会扩展。根据 r/ethstaker 调查的结果,也可以合理地假设,至少在较低的质押级别上,质押者是业余爱好者,并且不将维护和保养成本考虑在内。随着质押运营规模的扩大,我们预计个人质押者在选择其最佳方案时开始将维护和保养成本考虑在内。
此外,我们假设通过 cSSP 进行质押的可变成本超过通过 dSSP 进行质押的可变成本。此假设基于以下观察:除了质押的固有风险(例如,削减风险)之外,中心化交易所还引入了额外的托管风险——这些风险在 Lido 等去中心化质押服务提供商中是不存在的,后者不托管用户的资产。此外,通过中心化解决方案进行质押的机构质押者可能会产生额外的法律成本。最后,我们假设对于所有质押方法 jj,\alpha_{j} > 1αj>1。这允许凹利润函数,以便存在内部解。在代理人面临对其选择没有约束性约束(例如预算约束)的模型中,此假设是标准的。
总的来说,由于我们的校准方法的论证性质,我们认为以下呈现的结果不应被解释为预测点估计值。相反,重点应该放在在正在考虑的两个发行时间表下观察到的纳什均衡之间的相对变化和动态上。
下表总结了为后续比较分析选择的参数设置。
表 3:参数设置摘要
| 参数 | 描述 | 参数值 |
|---|---|---|
| N_{ss}Nss | 专家 类型代理的数量 | N_{ss} = 25'000Nss=25′000 |
| N_tNt | 技术人员 类型代理的数量 | N_t = 200'000Nt=200′000 |
| N_rNr | 零售商 类型代理的数量 | N_r = 925'000Nr=925′000 |
| y_{v}yv | 年度 MEV 收入 | y_{v} = 300'000yv=300′000 |
| y_{d}yd | 年度 DeFi 收益 | y_{d} = 0.02yd=0.02 |
| f_dfd | dSSP 费用 | f_d = 0.1fd=0.1 |
| f_cfc | cSSP 费用 | f_c = 0.25fc=0.25 |
| C_{ss}Css | 单独质押的固定成本参数 | C_{ss} = 0.4Css=0.4 |
| c_{ss}css | 单独质押的可变成本参数 | c_{ss} = 0.00053css=0.00053 |
| \alpha_{ss}αss | 单独质押的指数成本函数 | \alpha_{ss} = 2αss=2 |
| C_{t}Ct | 通过 dSSP 进行 技术人员 质押的固定成本参数 | C_{t} = 0Ct=0 |
| c_{t}ct | 通过 dSSP 进行 技术人员 质押的可变成本参数 | c_{t} = 0.0038ct=0.0038 |
| \alpha_{t}αt | 通过 dSSP 进行 技术人员 质押的指数成本函数 | \alpha_{t} = 1.5αt=1.5 |
| C_{r}Cr | 通过 cSSP 进行 零售商 质押的固定成本参数 | C_{r} = 0Cr=0 |
| c_{r}cr | 通过 cSSP 进行 零售商 质押的可变成本参数 | c_{r} = 0.0048cr=0.0048 |
| \alpha_{r}αr | 通过 cSSP 进行 零售商 质押的指数成本函数 | \alpha_{r} = 1.5αr=1.5 |
质押结果
通过这种校准,我们检查了每个发行时间表下的纳什均衡质押行为。当我们考虑包括单独质押者面临更高的 MEV 变异性和存在不专心的零售质押者的模型时,我们重点介绍了关键发现。基线模型和/或没有不专心零售商的模型的结果可以在 完整报告 中找到。
结果显示在下表中:
表 4:跨不同发行时间表的扩展模型的纳什均衡比较
| 类型 | 数量 | yi(D) | y'i(D) | Δ | |||||
|---|---|---|---|---|---|---|---|---|---|
| 存款 | 比率 | 利润 | 存款 | 比率 | 利润 | 存款 | 利润 | ||
| --- | --- | --- | --- | --- | --- | --- | --- | ||
| ss | 25K | 0.8M | 2.4% | 0.6% | 0.57M | 2.2% | 0.0% | -26.9% | -100% |
| t | 200K | 18.1M | 54.7% | 1.8% | 13.7M | 53.3% | 1.6% | -24.3% | -11.1% |
| i | 300K | 7.7M | 23.3% | 1.0% | 4.9M | 19.1% | 0.8% | -36.4% | -20.0% |
| r | N/A | 6.5M | 19.6% | N/A | 6.5M | 25.3% | N/A | 0.0% | N/A |
| 总计 | 33.1M | 25.7M | -22.4% | ||||||
| a 每个质押 ETH 的利润 |
可以做出以下观察:
- 观察 4: 总体质押供应量下降了 22.4%,低于所有 ETH 持有者都在战略性地采取行动的基线模型(参见 完整报告)。这可以解释为我们假设一部分质押者不对发行曲线的变化做出反应。
- 观察 5: 调整其供应量的 ETH 持有者类型在新时间表下失去了市场份额。当一种 ETH 持有者类型不对发行量减少做出反应而没有修改其质押供应量时,即特别缺乏弹性时,其他更具弹性的类型所做的调整往往会变得更加明显。值得注意的是,专家(单独质押者)的降幅大于受益于外部 DeFi 收益的 技术人员,导致专家的每个 ETH 质押利润甚至更低。此外,技术人员的存款相对减少(-24.3%)大于零售商和机构的相对减少(-19\%= 2.8/(6.5+7.7)−19%=2.8/(6.5+7.7))。在此基础上,可以认为,由于去中心化质押解决方案的市场份额下降幅度大于中心化解决方案(例如中心化交易所提供的解决方案)的市场份额,因此网络中的去中心化程度可能会因发行时间表的变化而受到影响。
- 观察 6: 即使在当前的发行时间表下,单独质押者的每个 ETH 质押利润也低于 技术人员 或 零售商。虽然这超出了模型的范围,但单独质押者因此有经济动机转变为 技术人员 或 零售商,而加入 技术人员 群体的激励更强。如果单独质押者选择不切换,这可能是由于对去中心化或利他主义的偏好(在这种情况下,由假设的市场细分来捕获)。
- 观察 7: 尽管质押供应量减少,但所有 ETH 持有者类型在调整后的发行时间表下都面临较低的每个 ETH 利润。单独质押者受此下降影响最大,这主要是由于为他们假设的成本函数,其中包括固定成本和更高的平均成本。如果排除固定成本,单独质押者的利润下降幅度将不那么严重。
- 观察 8: 发行收益的减少将单独质押者从正预期利润的情况带到负利润的情况。这可能意味着从单独质押迁移到其他质押替代方案,这将进一步降低去中心化程度,特别是如果一些单独质押者成为零售商。同样,这超出了模型的范围,并且通过假设一个隔离的市场,我们基本上假设单独质押者对去中心化的强烈偏好完全限制了这种迁移。
具有市场力量的中介 dSSP
我们研究了具有市场力量的中介 dSSP 如何影响质押行为,重点不是解决其最佳费用,而是关注在发行时间表更改后其费用应调整的方向。也就是说,我们首先计算当前发行时间表和基线模型中假设的费用下 dSSP 的利润。然后,在更新后的发行收益率曲线下,我们简单地将新费用识别为将产生类似利润的费用,然后使用该费用来推导新的质押均衡。我们将 dSSP 的战略决策纳入模型以供未来研究。
下表报告了比较分析的结果:
表 5:具有中介 dSSP 的扩展模型的纳什均衡
| 类型 | 数量 | yi(D); fd = 10% | y′i(D); fd = 13% | Δ | ||
|---|---|---|---|---|---|---|
| 存款 | 比率 | 存款 | 比率 | 存款 | ||
| --- | --- | --- | --- | --- | ||
| ss | 25K | 0.9M | 2.4% | 0.6M | 2.2% | -26.9% |
| t | 200K | 18.0M | 54.5% | 13.4M | 52.5% | -25.5% |
| i | 300K | 7.7M | 23.3% | 5.0M | 19.6% | -35% |
| r | NA | 6.5M | 19.7% | 6.5M | 25.5% | 0.0% |
| 总计 | 33.1M | 25.5M | -22.7% |
同样,可以高亮显示几个观察结果:
- 观察 9: dSSP (Lido) 在发行收益率降低后,以 f_dfd 增加了 30\%30% 来响应。
- 观察 10: 质押分布变得更加集中。f_dfd 的增加主要影响技术人员的质押,从而降低了他们的参与度(请参阅与上表的比较)。反过来,机构受益于技术人员参与度的降低,与固定费用的均衡相比,提高了他们的质押水平——大约相当于技术人员参与度的降低。由于 cSSP 是机构质押的提供者,因此这种转变导致质押市场内的集中度更高。
讨论
总的来说,上述分析可能最适合捕获短期动态,并且可能无法完全反映长期的市场变化。通过构建,质押供应的收益弹性的经验估计捕获了由质押奖励的短期波动驱动的质押供应的短期变化。此外,博弈论模型基于 ETH 持有者类型的固定市场细分,并且不允许在质押方法之间切换。尽管如此,我们的分析可能能够捕获发行时间表变化对以太坊质押市场动态的重要短期影响。
经验证据和理论模型的比较分析都表明,与通过中心化提供商或流动性质押提供商进行质押的 ETH 持有者相比,单独质押者对收益变化的反应更为强烈。因此,在发行时间表减少的情况下,预计单独质押的市场份额会下降,而中心化交易所的市场份额预计会上升。这将对以太坊验证者集的去中心化程度产生重要影响。
此外,博弈论模型有助于阐明为什么单独质押者可能对共识收益的变化更敏感。其他质押方法通过更好的 MEV 访问和 DeFi 收益在市场上具有竞争优势,从而降低了它们的弹性,并间接导致单独质押者的敏感性增加,以及在发行量调整时的挤出效应。这强调了在发行量变化的同时考虑 MEV 燃烧等措施的必要性,因为它们可以在减轻单独质押者的竞争劣势方面发挥重要作用,并因此减轻发行量减少对单独质押者的负面影响。
最后,与所有其他质押类别相比,减少的发行时间表降低了单独质押的盈利能力。虽然长期影响超出了我们模型的范围,但从长远来看,这可能导致退出或转移到替代质押解决方案(例如,提供额外 DeFi 收益的 dSSP)。
我们希望该模型能够为未来的研究和扩展奠定基础。例如,未来的迭代可以提供对中介机构和不同类型质押服务提供商的战略行为的更详细描述。如上所示,这些实体在塑造整个质押市场如何响应发行量变化方面起着至关重要的作用,因此将它们纳入对于更全面的分析至关重要。
参考文献
- 发行水平的属性:潜在奖励曲线上的共识激励和可变性
- 终局质押经济学:针对性的案例
- 共识发行收益率曲线变化对以太坊验证器生态系统中竞争动态的影响
- 具有缓和发行的奖励曲线
- 最大可行的安全性:以太坊发行的新框架
- 即将到来的发行曲线的形状
- 原文链接: ethresear.ch/t/key-insig...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- Solana的区块构建之战 75 浏览
- 如何去中心化构建区块? 180 浏览
- Builder Codes & ERC-8021:修复链上归属问题 241 浏览
- 并行执行的谎言:为什么SOL和ZERO不是在与ETH竞争,而是在输给它的L2 283 浏览
- “夺旗”竞赛继续! 248 浏览
- EVM Gas 分析:新的执行跟踪数据 264 浏览
- 质押和链上信贷市场之间的微妙张力 341 浏览
- 以太坊应该停止担心扩展性,去做人们想要的东西 321 浏览
- Vitalik的L2重置:以太坊为何需要此航向修正 267 浏览
- 如何桥接到MegaETH(今天测试网,主网即将上线) 368 浏览
- 让挖矿带来更多完全验证的比特币用户 303 浏览
- CoW DAO月度回顾:2026年1月 - CoW DAO 316 浏览
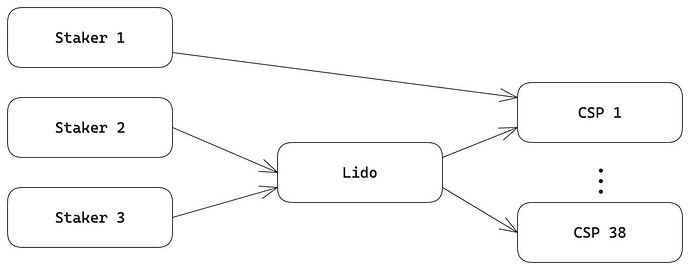 \
图 1:中间市场结构1280×501 28 KB
\
图 1:中间市场结构1280×501 28 KB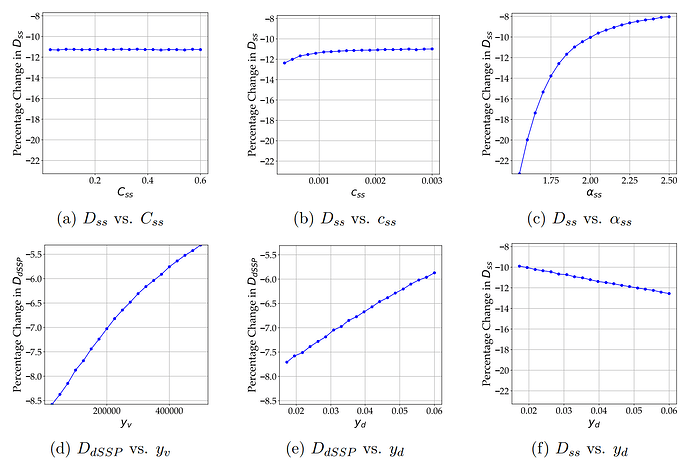 \
图 21545×1050 134 KB
\
图 21545×1050 134 KB
