密码学 - SM2曲线 - Asecuritysite
- asecuritysite
- 发布于 2025-08-29 10:01
- 阅读 1524
本文介绍了中国商用密码算法SM2,它定义了公钥密码,并与SM3(哈希函数)和SM4(加密算法)一起使用。文章通过代码示例展示了如何在OpenSSL中使用SM2曲线生成密钥对和进行签名,并解释了SM2曲线的参数以及签名输出的DER格式。

SM2 曲线
因此,NIST 将 AES 定义为对称密钥加密的标准。但是,NIST 被指出可能在推动一种带有 NSA 后门的密码。对于中国的公司来说,商密(SM)系列密码为 TLS 1.3 集成和无线身份验证提供了一种替代方案。其中,SM2 定义了公钥密码学,SM3 定义了一种哈希函数,SM4 用于加密。总体而言,SM4 由吕述望于 2007 年开发,并于 2016 年成为国家标准(GB/T 32907–2016)[ RFC 8998]。
在正常的椭圆曲线签名中,我们使用 secp256k1(如比特币和以太坊中所用)和 NIST P-256。那么,中国密码的等价物是什么呢?嗯,SM2 是一种由中国商用密码管理办公室定义的公钥方法。
对于后量子迁移,2020 年,中国密码学会 (CACR) 举办了一场比赛,并公布了 Aigi-sig、LAC.PKE 和 Aigis-enc 的获奖者,其中 Aigis-enc 是一种基于格的方法。PQMagic 是一个支持 FIPS 203、204 和 205 的 NIST 标准以及正在开发的中国标准的软件包 [ 这里]。
ECC
对于椭圆曲线密码学,我们从曲线的定义开始,例如:
y²=x³+ax+b (mod p)
这定义了 a、b 和 p 的值。接下来,我们选择曲线上一点作为基点(G),并生成一个随机标量值(d)。这是私钥,公钥是通过点乘生成的:
Q = d. G
在你的收件箱中获取 Prof Bill Buchanan OBE FRSE 的故事
这会在曲线上产生一个 (x, y) 点。
代码
运行一系列椭圆曲线的通用代码如下:
##include <stdio.h>
##include <string.h>
##include <stdlib.h>
##include <openssl/evp.h>
##include <openssl/pem.h>
##include <openssl/err.h>
##include <openssl/core_names.h>
##include <openssl/params.h>
##include <openssl/ec.h>
static void hexdump(const char *label, const unsigned char *buf, size_t len) {
printf("%s (%zu bytes): ", label, len); // label:标签, len:长度
for (size_t i = 0; i < len; i++) printf("%02X", buf[i]);
printf("\n");
}
// See https://github.com/openssl/openssl/discussions/24011
void print_parameter(const EVP_PKEY *pkey, const char *key_name) {
BIGNUM *param = NULL;
char *str = NULL;
if (EVP_PKEY_get_bn_param(pkey, key_name, ¶m)) {
str = BN_bn2dec(param);
fprintf(stdout, "%s: %s\n\n", key_name, str);
OPENSSL_free(str);
BN_free(param);
}
else {
fprintf(stderr, "Failed to fetch %s\n", key_name); // 无法获取 %s
}
}
static EVP_PKEY *generate_ecc(unsigned char *curve_name) {
EVP_PKEY *pkey = NULL;
EVP_PKEY_CTX *kctx = EVP_PKEY_CTX_new_from_name(NULL, "EC", NULL);
EVP_PKEY_keygen_init(kctx);
OSSL_PARAM params[3];
params[0] = OSSL_PARAM_construct_utf8_string(OSSL_PKEY_PARAM_GROUP_NAME, curve_name, 0);
params[1] = OSSL_PARAM_construct_end();
EVP_PKEY_CTX_set_params(kctx, params);
EVP_PKEY_generate(kctx, &pkey);
printf("Curve Parameters:\n"); // 曲线参数
printf("Curve: %s\n\n",curve_name); // 曲线
print_parameter(pkey, OSSL_PKEY_PARAM_EC_P);
print_parameter(pkey, OSSL_PKEY_PARAM_EC_A);
print_parameter(pkey, OSSL_PKEY_PARAM_EC_B);
print_parameter(pkey, OSSL_PKEY_PARAM_EC_ORDER);
unsigned char g[256];
unsigned char pub[256];
unsigned char priv[256];
size_t len;
EVP_PKEY_get_octet_string_param(pkey, OSSL_PKEY_PARAM_EC_GENERATOR, g, sizeof(g), &len);
hexdump("Generator:",g,len); // 生成器
printf("\nKey generated:\n"); // 密钥已生成
print_parameter(pkey, OSSL_PKEY_PARAM_PRIV_KEY);
EVP_PKEY_get_octet_string_param(pkey, OSSL_PKEY_PARAM_PUB_KEY, pub, sizeof(pub), &len);
hexdump("Public key:",pub,len); // 公钥
EVP_PKEY_CTX_free(kctx);
return pkey;
}
void do_sign(EVP_PKEY *ed_key, unsigned char *msg, size_t msg_len, unsigned char *type)
{
size_t sig_len;
unsigned char *sig = NULL;
EVP_MD_CTX *md_ctx = EVP_MD_CTX_new();
unsigned char *instance="Ed25519ctx";
const OSSL_PARAM params[] = {
OSSL_PARAM_utf8_string ("instance", "Ed25519ctx", strlen(instance)),
OSSL_PARAM_octet_string("context-string", (unsigned char *)"Context string",strlen("Context string")),
OSSL_PARAM_END
};
EVP_DigestSignInit_ex(md_ctx, NULL, NULL, NULL, NULL, ed_key, params);
/* Calculate the required size for the signature by passing a NULL buffer. */ // 通过传递 NULL 缓冲区来计算签名所需的尺寸。
EVP_DigestSign(md_ctx, NULL, &sig_len, msg, msg_len);
sig = OPENSSL_zalloc(sig_len);
EVP_DigestSign(md_ctx, sig, &sig_len, msg, msg_len);
printf("\nMessage: [%s]\n",msg); // 消息
hexdump("\nSignature: ",sig,sig_len); // 签名
OPENSSL_free(sig);
EVP_MD_CTX_free(md_ctx);
}
int main(int argc, char** argv) {
ERR_load_crypto_strings();
OpenSSL_add_all_algorithms();
unsigned char *msg="Hello";
unsigned char *curve="SM2";
if (argc > 1) curve = argv[1];
EVP_PKEY *ec = generate_ecc(curve);
do_sign(ec,msg,strlen(msg),curve);
return EXIT_SUCCESS;
}如果我们运行 SM2 [ 这里]:
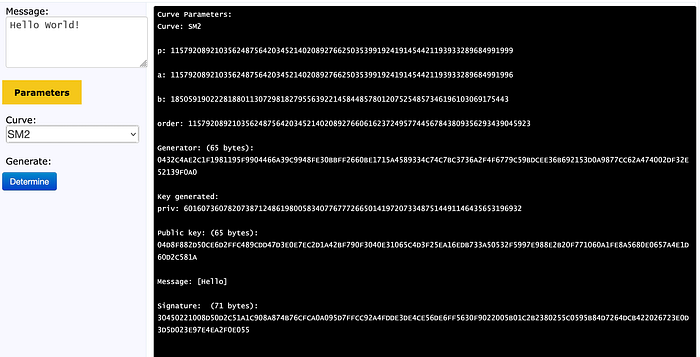
我们会得到:
Curve Parameters:
Curve: SM2
p: 115792089210356248756420345214020892766250353991924191454421193933289684991999
a: 115792089210356248756420345214020892766250353991924191454421193933289684991996
b: 18505919022281880113072981827955639221458448578012075254857346196103069175443
order: 115792089210356248756420345214020892766061623724957744567843809356293439045923
Generator: (65 bytes): 0432C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0
Key generated:
priv: 60160736078207387124861980058340776777266501419720733487514491146435653196932
Public key: (65 bytes): 04D8F882D50CE6D2FFC489CDD47D3E0E7EC2D1A42BF790F3040E31065C4D3F25EA16EDB733A50532F5997E988E2B20F771060A1FE8A5680E0657A4E1D60D2C581A
Message: [Hello]
Signature: (71 bytes): 30450221008D50D2C51A1C908A874B76CFCA0A095D7FFCC92A4FDDE3DE4CE56DE6FF5630F9022005B01C2B2380255C0595B84D7264DCB422026723E0D3D5D023E97E4EA2F0E055签名输出采用 DER 格式:
Signature: (71 bytes): 30450221008D50D2C51A1C908A874B76CFCA0A095D7FFCC92A4FDDE3DE4CE56DE6FF5630F9022005B01C2B2380255C0595B84D7264DCB422026723E0D3D5D023E97E4EA2F0E055如果我们解析它,我们会得到 [ 这里]:
DER: 30450221008D50D2C51A1C908A874B76CFCA0A095D7FFCC92A4FDDE3DE4CE56DE6FF5630F9022005B01C2B2380255C0595B84D7264DCB422026723E0D3D5D023E97E4EA2F0E055
[U] SEQUENCE (30)
[U] INTEGER (02): 63918914096015021337996337703255315669196085506087173836842003020883651080441
[U] INTEGER (02): 2572723738231390795708557834673807022247369723139243471919621030854542811221
-----BEGIN PUBLIC KEY-----
MEUCIQCNUNLFGhyQiodLds/KCgldf/zJKk/d495M5W3m/1Yw+QIgBbAcKyOAJVwFlbhNcmTctCICZyPg09XQI+l+TqLw4FU=
-----END PUBLIC KEY-----它们是 (r,s) 的值。
曲线的著名值是 [ 这里]:
A 等于 fffffffeffffffffffffffffffffffffffffffff00000000fffffffffffffffc,
B 是 28e9fa9e9d9f5e344d5a9e4bcf6509a7f39789f515ab8f92ddbcbd414d940e93
曲线的阶是 115792089210356248756420345214020892766061623724957744567843809356293439045923。
如果我们用 Python 检查,我们会得到:
>>> hex(115792089210356248756420345214020892766250353991924191454421193933289684991996)
'0xfffffffeffffffffffffffffffffffffffffffff00000000fffffffffffffffc'
- 原文链接: medium.com/asecuritysite...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 神奇的 Zig、C 和 OpenSSL 195 浏览
- 配对密码学之美:聚合签名和阈值签名 304 浏览
- 配对密码之美:聚合签名和阈值签名 524 浏览
- Shamir份额的魔力:BLS门限签名 463 浏览
- 英国银行与后量子密码技术 322 浏览
- Solana安全检查清单:Anchor和原生程序的45个关键检查项 451 浏览
- 量子计算与区块链:匹配紧迫性与实际威胁 1097 浏览
- 基于哈希函数的签名(二):少量次数签名 874 浏览
- Zig 签名(Ed25519 和 ECDSA) 1230 浏览
- 2026年:PQC密钥交换启动 524 浏览
- 2026年:PQC签名迁移的启动 2366 浏览
- 为PQC数字证书做好准备 941 浏览

