以太坊上实现隐私保护的 cWETH（confidential Wrapped ETH）方案

隐私对于以太坊的长期生存能力和可操作性至关重要。

遵循精彩的以太坊隐私：通往自决之路路线图，我们提出了一个保密 WETH 的概念，未来可能会发展成为一个成熟的保密代币标准 (EIP)。

很想听听你对草案的看法！

1. 简介

透明度是公共区块链的关键优势之一。然而，交易的公开可见性可能会损害用户的隐私。根本的挑战在于平衡区块链开放性的内在优势与个人保密的重要需求。

目标是创建一个无需许可的公共产品协议，通过加密用户的余额和转账金额来混淆 ETH 代币中的用户金融活动。这将允许在 ETH 中进行保密的点对点支付、捐赠和收购，而无需依赖中心化实体。

该提案建议完全在应用层中创建一个包装以太坊 (cWETH) 的保密版本。该解决方案结合了基于椭圆曲线 (EC) 扭曲 ElGamal 的承诺方案来保持机密性，以及 EC Diffie-Hellman (DH) 协议来引入受承诺方案限制的可访问性。为了强制执行承诺、加密和解密的正确生成，使用了 zk-SNARK。

1.1. 与现有协议的区别

至少有两种已知的解决方案不需要协议层修改，并且可以按原样实现。

Solana 和 Zether 方法乍一看可能非常相似，因为它们也使用 ElGamal 承诺。然而，主要的区别因素是需要解决离散对数问题才能访问加密余额。

Solana 通过维护一个单独的可解密余额来部分缓解这种情况。但主要区别在于所使用的加密方案不支持聚合，并且这种余额主要用作缓存，当挂起的金额转移到实际金额时会更新。但是，仍然需要解密表示为 ElGamal 承诺的余额，这重新引入了解决离散对数问题的必要性。虽然可以通过将值分成块来简化此过程，但 cWETH 协议提出了一种可聚合的加密方案，并与 ElGamal 承诺一起管理，以避免完全计算离散对数。

另一个区别在于 cWETH 使用的 ZK 证明。Solana 和 Zether 方法都依赖于 Sigma 协议和 Bulletproofs，而该提案基于 zk-SNARK。这里的权衡是需要可信设置，但这可以通过使用现有的可信设置来缓解，例如 Plonk 的通用设置，该设置已被证明随着时间的推移是安全的。

2. cWETH 概述

2.1. 包装 ETH

设置保密帐户的过程被认为是 ETH 包装操作的一部分。除了通常的包装逻辑之外，在首次存入 cWETH 合同时，每个用户都会提供一个 babyJubJub 公钥，该公钥将用于管理余额。

此公钥用于代币金额的承诺和加密以及余额计算。密钥对生成和初始存款流程如下图所示：

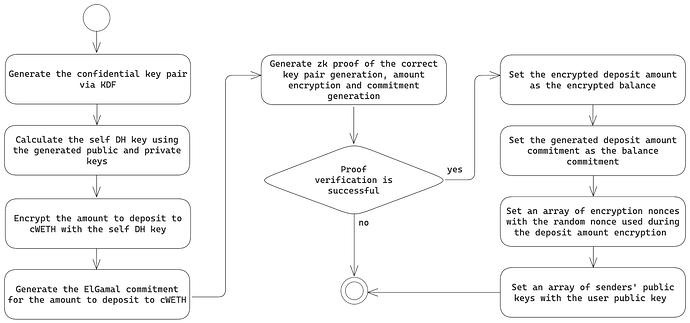
在首次存入 cWETH 合同后，初始余额将使用与保密转账相同的公式计算出的值进行更新，考虑到用户既是发送者又是接收者。与这些值和密钥对生成过程相关的技术细节将在本提案的后续章节中提供。

解包操作在概念上非常相似，因此本节将不介绍。

2.2. 余额管理

为了避免计算离散对数来计算用 ElGamal 隐藏的余额，需要维护两种并行的余额表示形式：

• ElGamal 承诺，仅用于验证余额知识的 ZK 证明。
• 使用 DH 共享密钥加密的余额，使用户能够解密其实际余额数据。需要访问发件人的公钥数组和加密 nonce 数组才能执行解密。

由于 ZK 证明是根据用户的当前余额生成的，因此在交易执行之前更改余额可能会使证明无效。为了解决这个问题，两种类型的余额（ElGamal 承诺和 DH 加密）都必须以两种不同的状态呈现：

• 待处理余额，用于接收代币。
• 实际余额，用于消费代币。

用户可以随时将其待处理余额中的代币转账到实际余额中。此外，它可以在用户发起的每次转账结束时完成。与两个单独的交易相比，这种方法会将余额更新合并为一个操作，从而减少 gas 的使用。

2.3. 保密转账

要发起保密转账，必须提供以四种不同形式表示的代币金额：

• 隐藏在接收方的基于公钥的 ElGamal 承诺中。
• 隐藏在发送方的基于公钥的 ElGamal 承诺中。
• 使用接收方的基于公钥的 DH 共享密钥加密，用于增加接收方的余额。
• 使用发送方的基于公钥的 DH 共享密钥加密，用于新的发送方余额。

下图说明了保密转账过程：

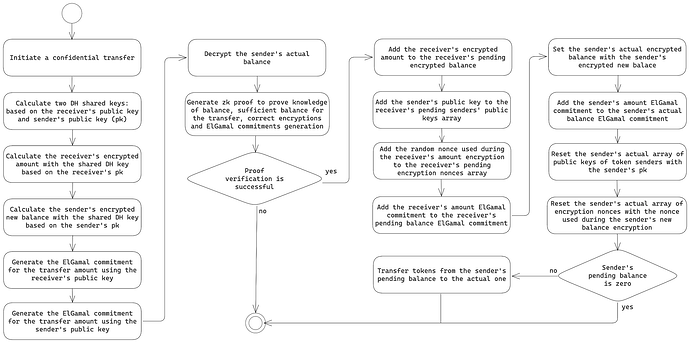
在传输过程中，两种类型的余额及其相关金额都会更新，以确保不同余额表示形式之间的一致性。

请注意，对于使用 DH 共享密钥加密和 ElGamal 承诺表示的相同值，存在两个单独的版本：基于发件人的公钥和基于收件人的公钥。这是由加密和承诺生成期间使用的不同方法引起的，其技术细节将在提案的后续章节中提供。

3. 保密性数学

3.1. 用于保密密钥对的 KDF

该协议利用确定性 KDF 方法来生成保密密钥对。用户必须使用其以太坊 (ECDSA) 私钥对 EIP-712 结构化消息进行签名。签名的哈希是 babyJubJub 私钥。

EIP-712 消息的获取方式如下：

bytes32 KDF_MSG_TYPEHASH = keccak256(“KDF(address cWETHAddress)”);

bytes32 kdfStructHash = keccak256(abi.encode(KDF_MSG_TYPEHASH, cWETHAddress));

babyJubJub 私钥的获取方式如下：

signature = eth_signTypedData_v4(kdfStructHash);

privateKey = keccak256(keccak256(signature));

请注意，切勿泄露签名，因为私钥直接从签名派生。

密钥对必须满足以下条件：

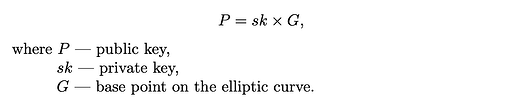
3.2. 基于 EC ElGamal 的承诺方案

基于 EC ElGamal 方案的承诺允许简洁的表示形式，适用于 ZK 证明。它还通过其加法同态属性促进无缝的余额管理。

余额的承诺包括两部分，并根据以下公式构建：

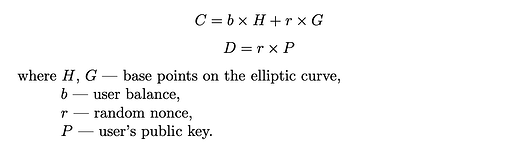
为了通过 ZK 证明有效地证明余额的承诺，用户必须使用私钥来补偿缺乏对聚合随机数 nonce 的知识：

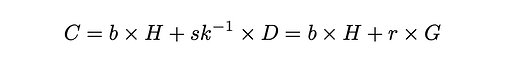
发送方和接收方的传输金额的承诺计算方式不同。接收方的金额承诺派生如下：

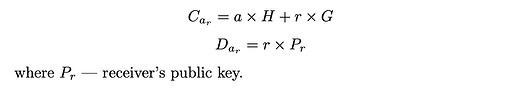
用于聚合发送方余额承诺的传输金额承诺的计算方式如下：

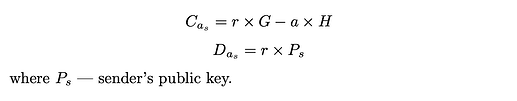
余额承诺以加法方式计算，如下所示：

3.3. 使用 EC DH 共享密钥进行加密

由于仅靠 ElGamal 承诺无法为用户提供访问解密余额的便捷方式，因此需要解决离散对数问题，因此使用 EC DH 共享密钥采用了一种通过加密隐藏金额的额外形式。

DH 共享密钥的派生方式如下：

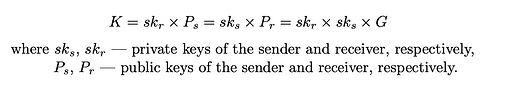
发送方和接收方执行的基于 DH 的传输金额加密方式不同。

用于聚合接收方余额的传输金额加密的计算公式如下：

需要使用随机数 nonce 来解决由于加密方案中缺乏随机性而导致的潜在传输数据泄漏问题，这在重复支付中尤其明显。必须将这些 nonce 值与发送方的公钥一起存储，以便用户可以解密其余额。

加密金额进一步用于聚合加密的接收方余额：

\ 1230×358 15.2 KB

根据以下公式，接收方可以按如下方式解密其余额：

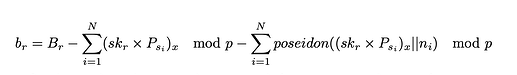
在发送方，使用此方法加密传输金额可能会导致管理无限数量的公钥和余额解密所需的随机数 nonce。为了解决这个问题，每次用户转移代币时，现有的发送方公钥和随机数 nonce 列表都会重置。这是通过计算新的加密发送方余额来实现的，如下所示：

更新加密余额后，发送方只需要管理自己的公钥和随机数 nonce 作为一个条目来解密拥有的代币总额。

用于计算新余额的相同逻辑可用于解包 cWETH 代币。

4. Solidity 智能合约

4.1. 状态变量

4.1.1. 公钥

首先，每个用户都与首次存入 cWETH 合同时生成的相应公钥关联。这在简单的 mapping(address => uint256[2]) 中进行管理。

4.1.2. 余额

每个用户的余额以 ElGamal 承诺形式表示：

struct Commitment {
    uint256[2] C;
    uint256[2] D;
}

为了解密使用 DH 共享密钥加密的余额，除了 DH 余额本身之外，还需要存储发送方的公钥数组和加密 nonce 数组：

struct DHBalance {
    uint256 encryptedBalance;
    uint256[][2] sendersPublicKeys;
    uint256[] encryptionNonces;
}

由于两种余额类型都必须以待处理余额和实际余额的形式提供，因此最终的余额存储如下所示：

struct Balance {
    Commitment elGamalCommitmentPending;
    Commitment elGamalCommitmentActual;
    DHBalance dhEncryptedPending;
    DHBalance dhEncryptedActual;
}

mapping(uint256 => Balance) internal balances;

请注意，内部余额核算使用用户的公钥的 x 坐标作为余额映射中的密钥。

4.2. 函数

4.2.1. 存入 cWETH

为了正确创建保密帐户，必须提供 deposit 函数：

function deposit(
    uint256[2] publicKey,
    bytes calldata amountCommitmentData,
    bytes calldata balanceEncryptionData,
    bytes calldata proofData
) external payable;

除了常规的 ZK 证明之外，还需要 proofData 来确保用户实际拥有提供的公钥的私钥。

amountCommitmentData 进一步解码如下：

(uint256[2] commitmentC, uint256[2] commitmentD) = abi.decode(amountCommitmentData, (uint256[2], uint256[2]));

balanceEncryptionData 解码如下：

(uint256 encryptedBalance, uint256 encryptionNonce) = abi.decode(balanceEncryptionData, (uint256, uint256));

4.2.2. 保密转账

清楚地了解承诺和加密方案后，可以按如下方式指定 transfer 函数：

function transfer(
    address receiver,
    bytes calldata amountCommitmentData,
    bytes calldata amountEncryptionData,
    bytes calldata proofData
) external;

amountCommitmentData 进一步解码如下：

(uint256[2] senderCommitmentC, uint256[2] senderCommitmentD, uint256[2] receiverCommitmentC, uint256[2] receiverCommitmentD) = abi.decode(amountCommitmentData, (uint256[2], uint256[2], uint256[2], uint256[2]));

amountEncryptionData 解码如下：

(uint256 newEncryptedBalance, uint256 senderEncryptionNonce, uint256 receiverEncryptedAmount, uint256 receiverEncryptionNonce) = abi.decode(amountEncryptionData, (uint256, uint256, uint256, uint256));

4.2.3. 提取 cWETH

为了解包 cWETH 代币，必须提供 withdraw 函数：

function withdraw(
    uint256 amount,
    bytes calldata amountCommitmentData,
    bytes calldata balanceEncryptionData,
    bytes calldata proofData
) external;

amountCommitmentData 进一步解码如下：

(uint256[2] commitmentC, uint256[2] commitmentD) = abi.decode(amountCommitmentData, (uint256[2], uint256[2]));

balanceEncryptionData 解码如下：

(uint256 newEncryptedBalance, uint256 encryptionNonce) = abi.decode(balanceEncryptionData, (uint256, uint256));

5. Circom 电路

本提案中描述的每个参数都旨在可在链上验证并与零知识电路兼容。

5.1. 存入 cWETH 电路

存款到 cWETH 证明的电路信号列表如下：

公共信号：

• 用户公钥；
• 存款金额；
• 用户余额的 ElGamal 承诺；
• 存款金额的 ElGamal 承诺；
• 使用基于用户公钥的 DH 密钥加密的存款后用户余额；
• 加密随机数 nonce。

私有信号：

• 用户私钥；
• ElGamal 承诺中使用的随机数 nonce。

操作这些信号，电路必须具有以下约束：

1. 提供的私钥确实是提供的公钥的私钥。
2. 提供的存款金额被证明是使用基于 ElGamal 的承诺提交的金额。
3. 存款后用户的余额被证明是使用 DH 共享密钥加密的余额。

5.2. 保密传输电路

保密传输证明的电路信号列表如下：

公共信号：

• 发送方公钥；
• 接收方公钥；
• 发送方余额的 ElGamal 承诺；
• 基于发送方公钥的传输金额的 ElGamal 承诺；
• 基于接收方公钥的传输金额的 ElGamal 承诺；
• 使用基于发送方公钥的 DH 共享密钥加密的新发送方余额；
• 在发送方新余额加密中使用的随机数 nonce；
• 使用基于接收方公钥的 DH 共享密钥加密的传输金额；
• 在接收方传输金额加密期间使用的随机数 nonce。

私有信号：

• 发送方私钥；
• 发送方余额；
• 传输金额；
• 在发送方 ElGamal 承诺中使用的随机数 nonce；
• 在接收方 ElGamal 承诺中使用的随机数 nonce；

操作这些信号，电路必须具有以下约束：

1. 提供的私钥确实是提供的发送方公钥的私钥。
2. 提供的发送方余额被证明是使用 ElGamal 承诺提交的余额，并且大于或等于传输金额。
3. 发送方基于 ElGamal 的传输金额承诺已正确生成。
4. 接收方基于 ElGamal 的传输金额承诺已正确生成。
5. 新发送方余额已使用基于发送方公钥的 DH 共享密钥正确加密。
6. 传输金额已使用基于接收方公钥的 DH 共享密钥正确加密

5.3. 从 cWETH 电路提取

从 cWETH 提取证明的电路信号列表如下：

公共信号：

• 用户公钥；
• 接收方地址；
• 提取金额；
• 用户余额的 ElGamal 承诺；
• 基于用户公钥的提取金额的 ElGamal 承诺；
• 提取后使用基于用户公钥的 DH 共享密钥加密的余额；
• 在新余额加密期间使用的随机数 nonce。

私有信号：

• 用户私钥；
• 用户余额；
• 在 ElGamal 承诺中使用的随机数 nonce；

操作这些信号，电路必须具有以下约束：

1. 提供的私钥确实是提供的公钥的私钥。
2. 提供的发送方余额被证明是使用 ElGamal 承诺提交的余额，并且大于或等于提取金额。
3. 提取金额的 ElGamal 承诺已正确生成。
4. 新余额（提取后）已使用基于用户公钥的 DH 共享密钥正确加密。

参考文献

Solana 基金会 - 保密代币扩展。2022.

Benedikt B¨unz 等人。Zether：迈向智能合约世界的隐私。2020.

• ZEX v0.1：保密点对点 DEX

• 原文链接： ethresear.ch/t/confident...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～