ZK 编年史
ZK编年史:初探
- Frank Mangone
- 发布于 2025-11-11 18:14
- 阅读 1075
本文是关于零知识证明(ZK proofs)系列文章的开篇,旨在以更易于理解的方式介绍这一主题。文章首先解释了零知识证明的概念,即在不泄露任何额外信息的情况下,使某人相信某个陈述是真实的。然后,讨论了如何检验计算的正确性,并介绍了交互式证明系统(IP)及其完整性和可靠性。最后,文章指出零知识是这些证明系统可以具备的一个附加属性,用于保护敏感信息。
我一直在尝试启动这个系列的想法已经有一段时间了。
这个故事始于几个月前,当时我在一次会议上与一位同事交谈。在某个时候,我们开始讨论零知识证明(ZK 证明),特别是从哪里学习它们。
提到了一些不错的材料:例如,Rareskills 的零知识之书 和 Distributed Labs 的 ZK-DL 训练营。
顺便说一句,很棒的资源。请随意尝试一下!
但我的同事特别坚持一本书:Justin Thaler 的证明、论证和零知识。
我想当时我准备好迎接挑战,所以我第二天就在网上买了这本书,并在送到我家门口后立即开始阅读。
天啊。我以为这会很容易,因为我之前已经了解过这个主题。不用说,我非常非常错误。
我立刻清楚地意识到,我还有很多东西要学。在我的阅读过程中,我不乏那些 啊哈! 的时刻,而且我发现自己很多次都在思考,如果我在我的旅程中早些时候接触到某些概念,我会 绝对喜欢 的。
这就是我写作这个系列的动机:尝试以我希望在我第一次学习这个主题时向我展示的方式来指导你完成这个精彩的主题。
在我们开始之前,先快速声明一下:这不会容易。毕竟,这是一个具有挑战性的话题。但是,嘿,让我们尽量保持它的乐趣和吸引力!
好的!我想要回答的第一个问题是 我们到底要进入什么领域?因此,在深入研究任何花哨的数学之前,让我们首先看看几个关键概念。
设定期望
我将首先声明,零知识本身的想法在同等程度上是 令人困惑 和 具有误导性的。
令人困惑之处在于,简单的定义 本身就非常令人费解。在这里,你自己看看:
以零知识证明某事意味着我们在不泄露任何信息的情况下说服某人某个陈述的真实性,除了该陈述的真实性。
就像... 什么?

我们将有足够的时间来详细解释这一点,但作为几个快速的例子,想象一下:
- 向当地酒吧入口处的保安证明你已年满 21 岁,而无需向他出示你的身份证。听起来很神奇——如何在不实际向他们出示你的身份证并透露你的出生日期的情况下做到这一点?此外,还有他们不需要知道的其他信息,例如你的姓名或出生国家!
- 同样,想象一下,你可以证明你是一个精选团体的成员,从而获得进入酒吧 VIP 的资格——但是,同样,无需出示你的身份证。
- 一旦你到达那里,你就可以去酒吧,并向调酒师证明你有一些免费票券,而无需再次透露你的身份。
这些例子有点过分,但它们有助于概念化我们所追求的目标:隐私。保护 敏感数据,同时使用它来 证明 关于它的东西。
尽管如此,感觉还是很奇怪,不是吗?就像,我们到底该怎么做?
我保证,我们会到达那里的。通过一些奇怪的数学方法,但我们会到达那里。
你会发现还有其他一些经典的例子可以帮助巩固核心思想。我特别喜欢这里的这个视频——希望它有所帮助!
具有误导性的部分
我的第二个主张与零知识本身实际上不是一类密码学方法,而是一种 属性 有关。
你可能会问,什么属性?嗯……我不想剧透。
相反,我想让我们谈谈一个强大的想法,零知识稍后会很好地融入其中。
检查计算
这里有一个问题:你如何知道某些计算是否 正确执行?
起初,这可能听起来像一个愚蠢的问题。我的意思是,假设我们编写一些程序。当我们运行它时(即使它有错误),我们将得到一些输出,这是该特定程序的 正确输出。那么我们为什么要怀疑 正确执行 呢?
好的,让我们更进一步。假设我们的任务是实现一些复杂的算法。
只需选择你最喜欢的一个!Dijkstra 算法、FFT、矩阵乘法……任何让你感兴趣的。
现在我们 确实关心 错误。一个有缺陷的实现会导致不正确的结果,即使结果确实对应于执行的程序。
如果我们有一种 探测 我们的程序以确定它是否正常工作的方法,那将是太棒了——这通常就是 测试 的目的。我们可以通过检查我们的程序是否正确处理一些已知的情况,仅通过查看所述计算的 结果 来推断我们的程序是否有错误。
请注意,在这两种情况下,是我们 在运行程序。

好吧,废话
我知道,这起初可能看起来是一件显而易见的事情。但是现在想象一下,你必须运行一些 巨大的程序——类似于训练大型语言模型,或者运行一个非常复杂的物理模拟,甚至是解决一个巨大的数独。
除非你有一台非常强大的计算机(或者至少,你有一台比我用来写这篇文章的烤面包机更好的计算机),否则你很可能会避免运行这些程序,因为得到一个解决方案会花费 太长时间。
你能看到这是怎么回事吗?你可能无法执行这些程序,但是 其他人可能会,他们可能只是 把结果交给你。
那么现在,你如何知道 结果 是正确的?
可验证计算
根据我们正在处理的问题,以及结果应该是什么样子,我们可能能够对接收到的值执行 一些检查。
以数独为例。

有人可能 声称 他们有一个给定难题的解决方案。你如何检查该解决方案是否真的 有效?
很简单——只需检查难题中的每一行、每一列和每个正方形的 总和 是否等于正确的值。作为 验证者,我们不关心难题是如何解决的,而只检查结果是否符合预期。
这可能看起来不多,但实际上 非常强大。这里起作用的关键见解是,执行某些计算 和 验证其结果 可能是截然不同的事情。
不仅如此,验证可能比原始执行快得多。
当然,解决数独并不是特别令人兴奋。但我向你保证——这种简单的分离确实能够实现各种很酷的行为。
这只是可能发生的事情的一瞥。我真的很想给你更多的例子,但这在我们的旅程中 为时过早。我们首先必须复习一些数学基础知识,才能真正开始挖掘好东西。
尽管如此,在继续学习之前,我们还可以说一些事情。
证明系统
我知道我说过我们会稍后讨论数学基础知识——但是我们需要 一些 数学来完成本文的其余部分。所以我撒了谎。抱歉!

Muehehehe
让我们想象一下,我们一直在谈论的这个“程序”由某个函数 f 表示。那么我们的目标可以描述如下:证明者(将计算 f)将尝试说服 验证者(将接收计算的输出)对于某些输入 x 的 正确结果 是某个 声明的值 y,如下所示:
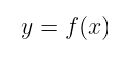
y = f(x)
这里要说的第一件事是有两个非常不同的角色。我们总是会谈论 证明者 和 验证者——有时,可能会出现其他角色。
其次,我们可能会问“说服”是如何发生的。你看,并非所有程序都像数独那样易于检查,有时,仅凭结果 是不够的。
我们将要做的是允许证明者和验证者 相互交谈。通过交换一些非常具体的消息——我们将在即将到来的文章中更详细地看到这些消息——验证者可以收集关键信息,这些信息最终将使他们能够执行这些检查。
这就是所谓的 交互式证明系统(或简称为 IP),也是我们将在本系列中研究的协议类型。交换的消息序列称为 转录,我们可以将完整的转录视为计算 f(x) = y 的 正确性证明。
我知道这一点现在有点抽象,但我保证,我们很快就会看到它在实践中是如何运作的。
属性
如果你向上滚动到本节的开头,你会注意到我明确地说 y 是评估 f(x) 的 声明的结果。从一开始就理解这一点非常重要:既然验证者不执行实际计算,这意味着证明者 可以尝试说谎。
让我们再说一遍:
证明者可能不诚实
至关重要的是,我们提出的任何 说服 验证者的系统都可以 抓住谎言中的证明者。这被形式化为我们需要我们的交互式证明具有的 两个属性:
- 完整性:如果证明者是 诚实的,那么验证者将 几乎总是接受 我们的证明。
- 可靠性:如果证明者是 不诚实的,那么 几乎不可能 制作一个令人信服的证明。
是的,我说的是 几乎:存在一种很小的可能性,即有效的证明可能会被拒绝,或者一个不诚实的证明者可能会作弊。我们将这些概率称为 完整性 和 可靠性 误差,当然,我们的目标是使这些概率尽可能小。
这本质上是验证者不自己执行计算的 代价:少量的不确定性。
但总的来说,我们将尝试使这种概率 非常非常小——以至于证明者 几乎不可能 作弊。有时,完整性误差甚至可以是 零,因此验证者将 始终接受 来自诚实证明者的证明。
零知识在哪里?
你是否注意到,在前面的两节中,我们 没有说 任何关于零知识的内容?
这就是我所说的具有误导性的部分:可验证计算本身可能非常强大,没有零知识。许多应用程序甚至不关心零知识部分,而是利用这些证明系统的其他良好属性,例如证明可以 很小 并且 验证速度很快。
正如我已经提到的,零知识是这些证明可能具有的 额外属性。
它与 隐藏 函数 f 的一些输入有关。此函数的作用是对输入执行某种类型的 检查。
还记得我们之前在酒吧举的例子吗?假设我的年龄是一些值 x,我有一个函数,如果 x > 21,则输出 1,否则输出 0。我想要的是证明 f(x) = 1,但不透露 x。
当我们想要对某些敏感信息进行 保密 时,此零知识属性将非常重要——例如,在我们需要私有交易、匿名凭证或机密投票的应用程序中。
但是,我们这样做的方式将在以后的文章中介绍。
总结
好的,我认为对于我们进入零知识的第一步来说,这已经足够了!
快速回顾:我们看到执行和验证不是同一件事,这使我们可以将执行的压力从 验证者 转移到 证明者,代价是必须构建一个 证明系统。这是可取的,因为验证可以比执行 快得多。
我们还提到,这些证明系统将是 交互式的:在证明者和验证者之间来回发送消息,直到验证者 确信 计算已正确执行。
我们可以做一些事情来 消除 对这种交互的需求,但我们稍后会讨论。
然后,我们提到了我们需要保证这些证明有意义的两个关键属性:完整性 和 可靠性。简而言之,这些意味着当计算结果 实际正确时,应该很容易证明结果的正确性,并且作弊很难。
零知识类似于所有这些之上的樱桃。这不是一个严格的要求,但它可以添加到组合中。当它是时,我们可以创建这种保护隐私的证明系统,这在正确的上下文中可能非常有用。
我认为到目前为止,这仍然听起来很抽象,并且说实话,有点神奇。
并且要完全透明地说明,在几篇文章中仍然如此——请耐心等待!
为了消除这种神秘的面纱,我们需要深入研究为这种密码学机制提供动力的基本数学。
我们将在下一篇文章中再见!
- 原文链接: medium.com/@francomangon...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
