Uniswap v3中的恒定乘积公式

跳转到主要内容 跳转到页脚

Uniswap v3 中的常数乘积公式

我们的目标是根据一个区段的真实储备推导出常数乘积公式，公式如下：

L2=(xr+Lpu)(yr+Lpl)

并从那里恢复前一章中获得的一些公式。

本章是可选的。与前几章相比，它没有引入任何根本性的新概念，而是提供了从价格和流动性推导真实储备的不同视角。可以跳过它，而不会对本书的其余部分产生任何不利影响。

Uniswap 是一种常数乘积自动做市商。在 Uniswap v2 中，如果我们忽略费用，池中的交换遵循公式 xy=k 中的常数 k 保持不变的规则，其中 x 和 y 代表池中 X 和 Y 代币的储备。从这个意义上讲，可以说公式 xy=k 定义了池中交换的行为。

Uniswap v3 也是一个常数乘积 AMM，主要区别在于池没有恒定的流动性，而是由多个曲线段组成，每个曲线段都有一定的流动性 L。

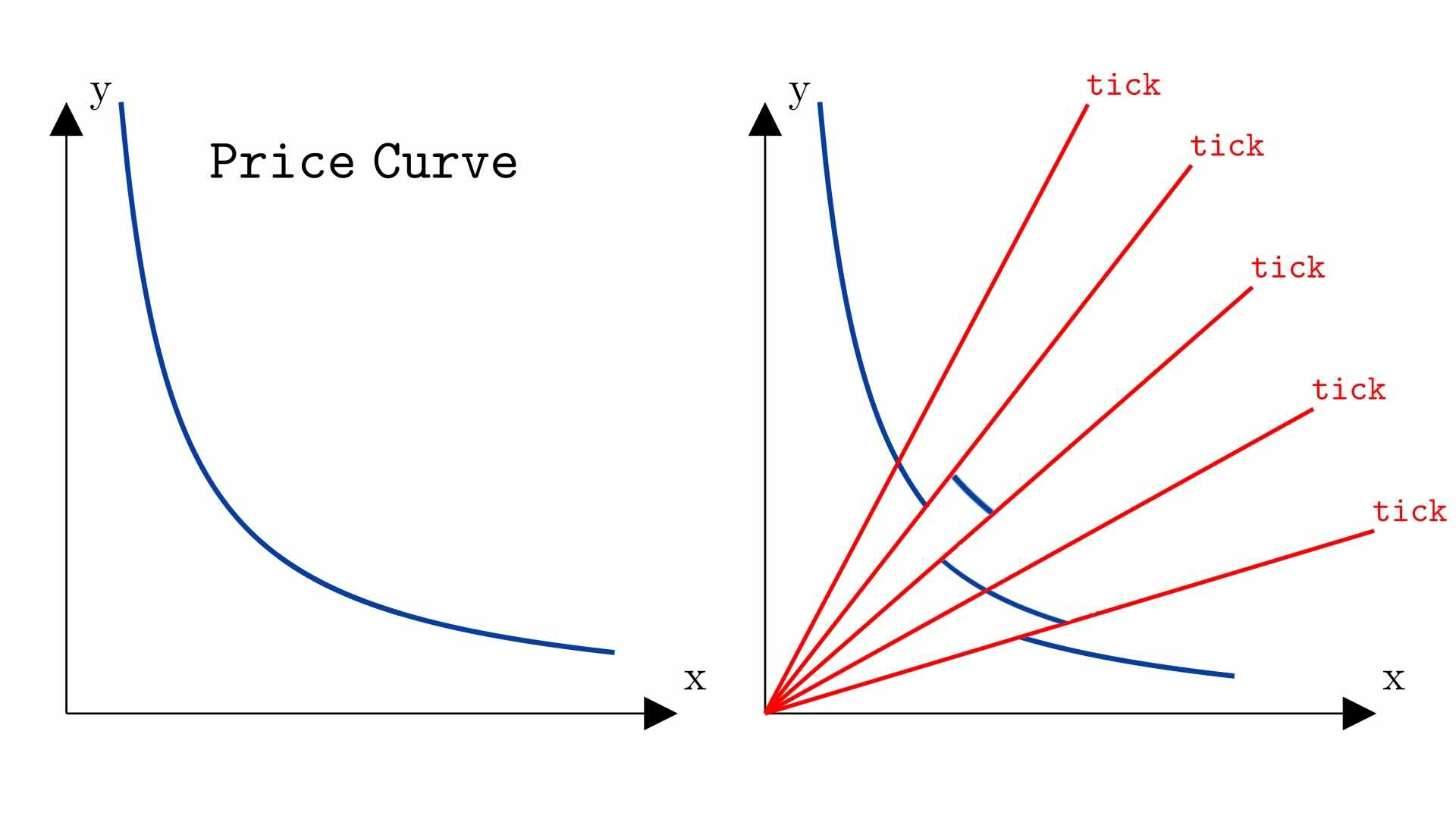
在每个区段中，交换都遵循与 Uniswap v2 相同的行为，并且在忽略费用的情况下，只要交换不越过区段的边界，就必须在公式 L2=xy 中保持 L 值的恒定。

因此，区段中控制交换的公式仍然是 L2=xy。但是，与 Uniswap v2 不同，x 和 y 不是区段的真实储备，而是它的虚拟储备，即如果该区段延伸到无限曲线，它将拥有的储备（参见关于真实和虚拟储备的章节）。

有人可能会问，一个区段的常数乘积公式 L2=xy 是否可以用该区段的真实储备而不是其虚拟储备来表示。答案是肯定的。事实上，这个公式可以在 Uniswap v3 白皮书的第 2 页找到，如下所示（这里，x 和 y 表示真实储备，我们在我们的表示法中将其表示为 xr 和 yr）。这与引言中显示的公式相同。

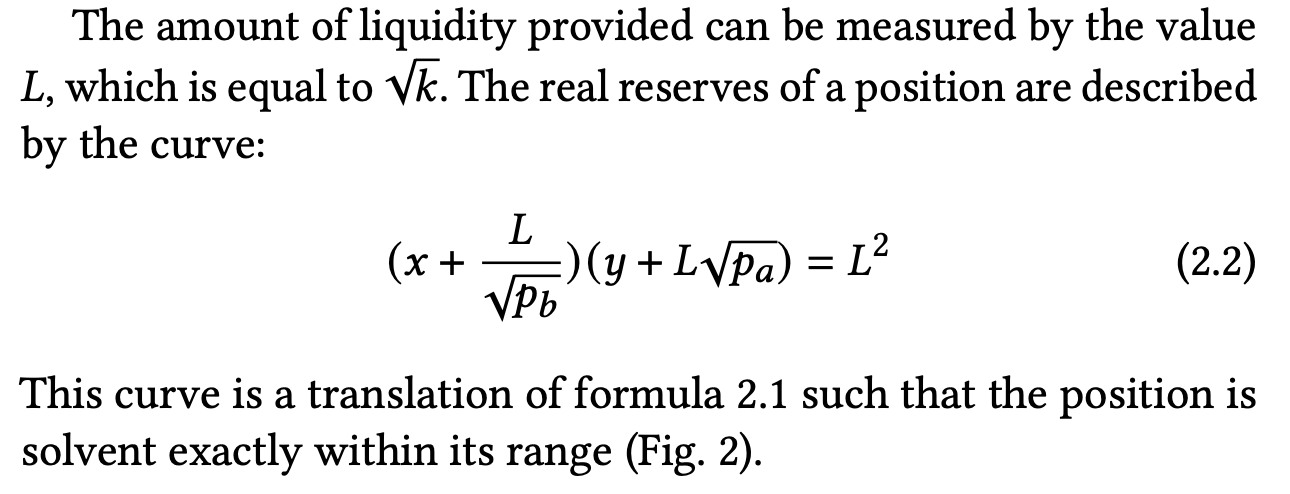
上面的公式建立了流动性、区段边界和真实储备之间的关系。在我们的表示法中，这个公式应该写成

L2=(xr+Lpu)(yr+Lpl)

其中 pl 是较低 tick 的价格，pu 是较高 tick 的价格，L 是流动性。

对于给定的区段，这些值是固定的，而真实储备是变化的。这类似于 Uniswap v2，其中流动性 k 在 k=xy 中是固定的，而储备 x 和 y 可以改变。在这两种情况下，公式都约束了可能的储备值——如果一种代币的储备增加，另一种代币的储备必须减少，以便流动性保持不变。

在下面的互动工具中，可以更好地看到这个想法。你可以选择较高的 tick、较低的 tick、区段的流动性和当前价格。随着价格的移动，真实储备 xr 和 yr 会发生变化，但以一种流动性 L 保持恒定的方式变化。换句话说，真实储备之间的比例不是任意的，而是完全由流动性和 tick 边界决定的。

双曲线可视化

Uniswap V3 常数乘积互动工具

移动黑色滑块以更改真实储备的组成

移动紫色滑块以更改流动性

移动绿色和蓝色滑块以更改区段边界

300.002=(88.62+300.003.49)⋅(190.05+300.000.32)

yᵣ = 190.05xᵣ =

88.62

L²90000

Pu3.49

PL0.32

v2 和 v3 之间的一个主要区别是，在 v3 中，其中一项储备可以达到零，而另一项储备不会接近无穷大。耗尽一个区段中一种代币的真实储备是正常的，此时价格会移动到下一个区段。

值得注意的是，常数乘积公式在代码库中任何地方都没有出现。在 Uniswap v2 中，协议可以简单地在交换中强制执行常数乘积公式。但是，在 v3 中，这更加复杂，因为在一次交换中，价格可能会穿过多个区段。

尽管如此，常数乘积公式可用于推导真实储备的表达式，这些表达式以区段边界、流动性和当前价格表示。我们已经在上一章中通过其他方式推导了这些公式，因此，本章是可选的。

然而，如果读者希望了解常数乘积公式的来源以及如何使用它来计算区段的真实储备，那么这就是本章的目的，我们邀请你继续。

关联区段中的真实和虚拟储备

一个区段的常数乘积公式与 Uniswap v2 中的相同，

L2=xy

但现在 x 和 y 是虚拟储备。

如果我们找到一种将虚拟储备与真实储备相关联的方法，我们可以推导出真实储备的常数乘积公式。

考虑下面的图示，其中 pl 是较低 tick 的价格，pu 是较高 tick 的价格。

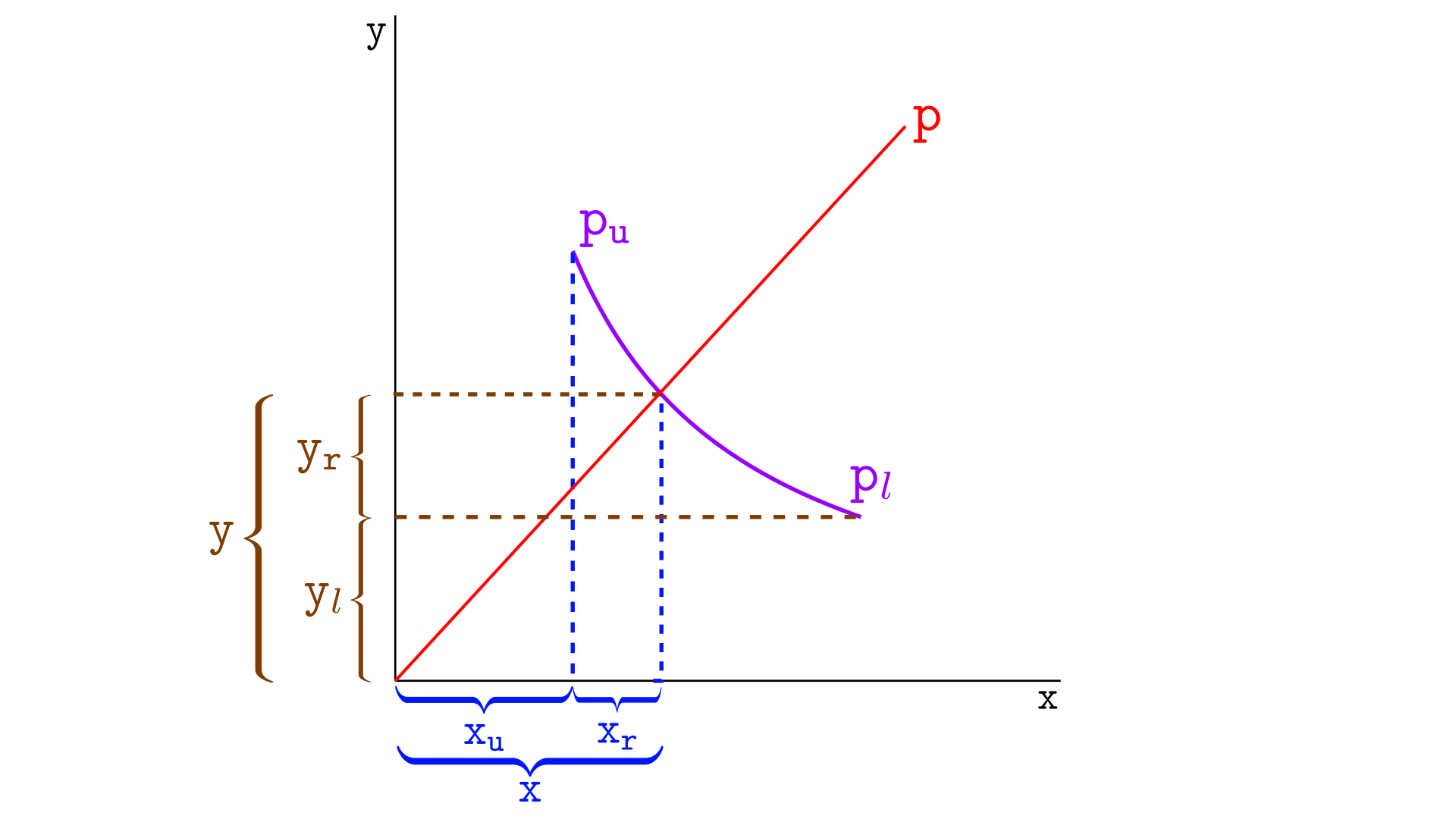
在上图中，我们有

• (x,y) 是当前价格的虚拟储备，
• yl 是 pl 处的 Y 的虚拟储备——如果它是一条无限曲线并且价格为 pl，则该区段将拥有的 Y 代币数量。但是，我们更感兴趣的是 yl 的几何意义，而不是其解释，
• xu 是 pu 处的 X 的虚拟储备，
• (xr,yr) 是区段的真实储备。

则虚拟储备和真实储备之间的关系由下式给出

y=yl+yrx=xu+xr

我们可以在 L2=xy 中使用这些关系，代入 x 和 y，得到

L2=(xu+xr)(yl+yr)

在一个区段中，xr 和 yr 可以在交换期间变化，但 xu 和 yl 仅取决于区段边界，因此它们对于该区段而言是常数。因此，如果我们能获得 xu 和 yl，我们就找到了所需的公式。我们在上一章中推导了获得 xu 和 yl 的公式，在下一节中，我们将使用这些公式来推导真实储备的常数乘积公式。

真实储备的常数乘积公式

在关于真实和虚拟储备的章节中，我们学习了如何从价格和流动性中找到一个区段的虚拟储备：x=L/p 和 y=Lp。我们可以使用这些公式来获得 xu 和 yl，如下所示：

xu=Lpuyl=Lpl

使用这些值，我们可以将常数乘积公式

L2=(xr+xu)(yr+yl)

写成

L2=(xr+Lpu)(yr+Lpl)

这个公式适用于流动性为 L 的区段，其中较低的 tick 为 pl，较高的 tick 为 pu。

现在我们有了一个常数乘积公式，它关联了流动性、真实储备和区段边界，而无需参考虚拟储备。

请注意，从真实储备计算一个区段的流动性并不简单，因为上面的公式在等式的两边都包含参数 L；这是一个关于 L 的二次方程。

在实践中，我们不必担心这个问题，因为协议不使用上述公式来计算流动性。相反，协议存储有关流动性的信息，并根据给定的流动性，计算两个价格之间的 X 和 Y 代币的真实储备。

因此，我们感兴趣的是找到一个基于区段的流动性、边界和当前价格来计算 xr 和 yr 的公式。

在上一章中，我们已经在没有任何参考常数乘积公式的情况下推导了这些公式——正如引言中所述，常数乘积公式对于此并非绝对必要。

出于教育目的，我们将使用常数乘积公式重新推导上一章中的公式。关键思想是，即使代码库中未使用常数乘积公式，但代码库确实使用了基于当前价格、流动性和区段边界计算真实储备的公式，并且这些公式可以从常数乘积公式中推导出来。

为了证明这一点，让我们对三种可能的情况进行推导：

1. 当当前价格等于或低于较低的 tick 时，因此只有 X 代币的真实储备，
2. 当当前价格等于或高于较高的 tick 时，因此只有 Y 代币的真实储备，
3. 当前价格在区段内时，因此 X 和 Y 代币都有真实储备。

让我们从当前价格等于或低于较低 tick 的情况开始

1. 区段中只有 X 代币

在区段只有 X 代币的情况下，则 yr 等于零，我们可以得出常数乘积公式来推导 xr，如下所示：

L2=(xr+Lpu)(0+Lpl)L2=(xr+Lpu)LplLpl=(xr+Lpu)等式两边除以Lplxr=Lpl–Lpu将 Lpu 移动到等式的另一边

请注意，这与我们在上一章中推导的公式相同。

现在让我们考虑区段仅包含 Y 代币的情况——当当前价格等于或高于较高的 tick 时。

2. 区段中只有 Y 代币

在区段只有 Y 代币的情况下，则 xr 等于零，我们可以得出常数乘积公式来推导 yr，如下所示：

L2=(0+Lpu)(yr+Lpl)L2=Lpu(yr+Lpl)Lpu=yr+Lpl等式两边乘以 puLyr=Lpu–Lpl将 Lpl 移动到等式的另一边

请注意，这与我们在上一章中推导的公式相同。

现在我们转向最后一种情况，即价格位于较低的 tick 和较高的 tick 之间。

3. 区段中的两种代币

当价格介于较低的 tick 和较高的 tick 之间时，该区段将同时具有 X 和 Y 代币。

常数乘积公式

L2=(xr+Lpu)(yr+Lpl)

不涉及当前价格，我们也无法仅从中计算 xr 和 yr。请注意，我们有两个未知数（xr 和 yr），但只有一个方程。为了解决这个问题，我们需要另一个方程。

我们知道，就虚拟储备而言，价格公式为 p=y/x。因此，就真实储备而言，我们有：

p=yx=yr+Lplxr+Lpu

现在我们有两个方程（常数乘积公式和价格）和两个未知数（xr 和 yr）。我们可以重新整理价格公式为：

p=yr+Lplxr+Lpuyr+Lpl=p(xr+Lpu)

左侧的项出现在常数乘积公式中，因此我们可以在那里替换它。

L2=(xr+Lpu)(yr+Lpl)L2=(xr+Lpu)p(xr+Lpu)替换了 (yr+Lpl)L2=(xr+Lpu)2pL=(xr+Lpu)p取平方根Lp=xr+Lpu等式两边除以 pxr=Lp–Lpu

现在我们有了 xr，我们可以在常数乘积公式中使用这个表达式来找到 yr：

L2=(xr+Lpu)(yr+Lpl)L2=(Lp−Lpu+Lpu)(yr+Lpl)使用了 xrL2=(Lp−Lpu+Lpu)(yr+Lpl)L2=(Lp)(yr+Lpl)Lp=yr+Lpl等式两边乘以 pLyr=Lp–Lpl

xr 和 yr 的公式与我们在上一章中获得的公式相同。

总结

流动性为 L，在较低 tick pl 和较高 tick pu 之间的区段的常数乘积公式由下式给出

L2=(xr+Lpu)(yr+Lpl)

其中 xr 和 yr 是 X 和 Y 代币的真实储备。

• X
• Telegram
• LinkedIn
• Email

• 原文链接： rareskills.io/post/unisw...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～