方差锁定费用 - 对 Monad 基础费用机制的博弈论深入研究
- thogiti
- 发布于 2025-10-17 07:40
- 阅读 1934
本文分析了 Monad 的基础费用控制机制中存在的漏洞,该机制容易受到生产者策略行为的影响,导致方差锁定和 Underfill→Harvest 攻击。文章提出了通过引入最小最大值守卫、稀缺性门控、定向自适应性等一系列修正方案,以提高机制的健壮性和抗操纵性,并通过模拟验证了这些修正方案的有效性。
概述
Monad 的 base-fee 控制器,其灵感来源于 RMSprop 等自适应优化器,旨在通过使 fee 的步长与 gas 使用量的短期方差成反比,来实现响应性而不抽搐。然而,在一个无需许可的区块链中,区块生产者控制着驱动这种方差估计的信号,即 gas 使用量 $g_k$。这种内生性将价格平滑器变成了一种战略杠杆,从而实现了两种主要的攻击:方差锁定(对价格发现的拒绝服务)和欠填充→收割(对 base fee 的短期挤压)。我们在模拟中重现了这些攻击,并验证了一组可直接使用的修复程序,这些修复程序可恢复可预测性和激励兼容性。
配套资产:
Jupyter Notebook:monad_basefee_mechanism_research.ipynb
工件:/mnt/data/monad_unified_artifacts(fee 轨迹、KPI、图表)
1. 机制回顾
设 $L$ 为区块 gas 限制, $T = 0.8L$ 为目标利用率。对于区块 $k$,gas 使用量为 $g_k \in [0, L]$,base fee 为 $b_k > 0$,Monad 的更新规则为:
$$ \begin{aligned} b_{k+1} = b_k \cdot \exp\left(\eta_k \cdot \frac{g_k - T}{L - T}\right),\ \etak = \frac{\eta{\max} \cdot \varepsilon}{\varepsilon + \sqrt{\sigma_k^2}}, \end{aligned} $$
其中,方差估计 $\sigma_k^2$ 来自于偏差 $d_k = T - g_k$ 的指数平滑“趋势”和“矩”:
$$ \begin{aligned} \text{trend}{k+1} &= \beta\,\text{trend}{k} + (1-\beta)\, dk,\ \text{moment}{k+1} &= \beta\,\text{moment}_{k} + (1-\beta)\, d_k^2,\ \sigma_k^2 &= \text{moment}_k - \text{trend}_k^2. \end{aligned} $$
该博客和我们的模拟使用 $\beta \approx 0.96$ (7 秒半衰期),$\eta{\max} = 1/28$,以及一个稳定器 $\varepsilon = T \cdot \text{eps_scale}$(因此单位与利用率残差匹配)。强制执行下限 $b{\min} = 100$ MON-gwei。
⚠️ 结构性不对称 归一化分母 $L - T = 0.2L$ 创建了一个内在的 ($-4 : +1$) 不对称性: $$\Delta_k = \frac{g_k - T}{L - T} \in [-4, +1] \quad \text{当 } T=0.8L \text{ 时}。$$ 一个空区块 ($g_k=0$) 产生 $\Delta_k = -4$,而一个完整区块 ($g_k=L$) 仅产生 $\Delta_k = +1$。这种不对称性是归一化的一个属性,而不是自适应增益。 即使具有固定的 $\eta_k$,向下移动也比向上移动大四倍。然后,自适应 $\eta_k$ 放大了这种结构性偏差。我们在第 3 节中依赖这个 (−4:+1) 的事实来推导 fee-sink 漂移。(有关后果,请参见第 3 节。)
2. 平滑 ≠ 可预测:内生性问题
只有当像“出价 $bk + \varepsilon$”这样的策略是可靠的,价格发布机制才能帮助用户。这需要可预测性:用户必须能够从公共历史中形成 $\mathbb{E}[b{k+1} \mid \mathcal{F}_k]$。在 Monad 的设计中,学习率 $\eta_k$ 是 $\sigma_k^2$ 的函数,而 $\sigma_k^2$ 来自于区块生产者选择的过去 $g_j$ 值。因此,$\eta_k$ 对于战略行为来说是内生的,而不是公共可观察值的固定函数。
形式上,对于对数价格 $p_k = \log(bk)$,增量为 $p{k+1} - p_k = \eta_k \Delta_k$。因为 $\etak = f({g{k-j}})$ 并且每个 $g_{k-j}$ 都是一个战略选择,所以在战略输入下,过程 ${p_k}$ 是非马尔可夫的。不存在用户可以将 base fee 视为外生价格信号的理性预期均衡。fee 路径的平滑性并不意味着可预测性或占优策略真实性 (DSIC)。
3. Fee-Sink 漂移:不对称性与方差意识的结合
即使在平均需求刚好达到目标 ($\mathbb{E}[\Delta_k] = 0$) 的情况下,base fee 也会表现出系统的向下漂移。这是 (−4 : +1) 不对称性与方差感知阻尼相结合的直接结果。
结果 1(在方差感知不对称下的向下漂移)。 设 $p_k = \log(b_k)$,$\Delta_k \in [-4, +1]$,以及 $f' \le 0$ 的 $\eta_k = f(\sigmak^2)$。如果正偏差(拥塞)是突发的,并且比负偏差(未填充)更能膨胀方差,那么 $$\mathbb{E}[p{k+1} - p_k] \;=\; \mathbb{E}[\eta_k \Delta_k] \;=\; \operatorname{Cov}(\eta_k, \Delta_k) \;<\; 0.$$ 拥塞 ($\Delta_k > 0$) 通常伴随着高方差(例如,NFT 铸造),从而抑制了 $\eta_k$。协调的欠填充 ($\Delta_k < 0$) 产生低方差,从而保持 $\etak$ 高。这种负协方差产生了一个偏向于 $b{\min}$ 的 fee-sink 偏差。
这是一个充分条件。 如果 $\sigma_k^2$ 在 $\Delta_k > 0$ 上的条件一阶随机大于在 $\Delta_k < 0$ 上的条件一阶随机,并且 $\eta_k$ 在 $\sigma_k$ 中是非递增的,则 $\operatorname{Cov}(\eta_k, \Delta_k) < 0$。
经验检查。 在notebook 中,我们报告了 $\sigma_k^2 \mid \Delta_k>0$ 与 $\sigma_k^2 \mid \Delta_k<0$ 的 ECDF 差距,以及具有置信区间的样本协方差 $\widehat{\operatorname{Cov}}(\eta_k, \Delta_k)$(参见 PartB_KPIs.csv;图 B4 中的内联标记)。
在我们的 B4 (欠填充→收割) 模拟中,尽管平均利用率接近目标(图 B4;PartB_KPIs.csv: time_at_min_s),但 base fee 还是 超过 40% 的时间都在 $b_{\min}$。该系统偏向于低估区块空间的价格。
4. 反身性陷阱:为什么方差感知从根本上是可博弈的
上面描述的漏洞不仅仅是参数选择中的错误,它们源于一个更深层次的结构性问题:一个反身性问题,这是任何将其敏感度建立在由战略代理控制的信号上的机制所固有的。
在标准的自适应优化(例如,RMSprop)中,该算法观察到一个被动的、外生的信号(来自固定损失 landscape 的梯度),并调整其步长以更快地收敛。landscape 不会对优化器对学习率的选择作出反应。
在 Monad 的 fee 市场中,情况是相反的:
- 该机制维护状态 $S_k = (\text{trend}_k, \text{moment}_k, \eta_k)$。
- 区块生产者观察 $S_k$,并选择 gas 使用量 $g_k$,以最大化他们的私人收益(小费 + MEV − 机会成本)。
- 他们的选择 $gk$ 直接更新状态:$S{k+1} = f(S_k, g_k)$。
- 然后,该机制使用 $S_{k+1}$ 设置下一个 base fee,这会影响未来生产者的激励。
这创建了一个闭环反馈回路,其中控制器的自适应规则是它试图regulation的战略环境的一部分。生产者不仅仅是对价格做出反应,他们还在引导价格发现过程本身。
与 EIP-1559 对比: 以太坊的机制是无记忆的,每个区块的更新仅取决于该区块的完整性,最大调整幅度为 12.5%(当 $\lvert g_k - T\rvert = T$ 时)。一个交替完全/空区块的生产者会导致 fee 振荡,但不能抑制该机制的响应性。没有状态 $S_k$ 可以操作,也没有学习率可以崩溃。该机制的敏感性是一个常数,而不是一个战略变量。Monad 的自适应性通过使 $\etak = f({g{k-j}})$ 将控制器本身转换为一个攻击面。
在数学上,这是一个斯塔克尔伯格博弈,具有自适应跟随者动态,其中领导者(机制设计者)提交一个更新规则 $f(\cdot)$,而跟随者(生产者)进行最佳响应,从而预测他们的行动将如何塑造未来的 $f(\cdot)$。均衡不是一个简单的纳什均衡,而是一个战略固定点: $$ \begin{aligned} g^* = \arg\max_{g} \Pi(g; f(S(g))), \end{aligned} $$ 其中 $S(g)$ 是由行动序列 $g$ 引起的state trajectory,而 $\Pi$ 是生产者的利润函数。
这导致了一个根本性的权衡:
| 目标 | 需要 | 冲突 |
|---|---|---|
| 对持续需求做出响应 | 当需求稳定时,高 $\eta_k$ | 战略参与者可以模仿稳定性来触发高 $\eta_k$ 以进行操作 |
| 对战略差异的鲁棒性 | 对 $V_k$ 的低敏感度或固定的 $\eta_k$ | 丢失了诚实突发事件期间自适应的好处 |
没有使用 $Vk = \mathrm{Var}(g{k-w:k})$ 作为控制输入的机制可以在对抗环境中同时实现这两个目标。 控制器依赖于生产者选择的行动的函数的统计量的那一刻,它就会创建一个用于操作的杠杆。战略波动与诚实波动在观测上是等价的;该机制无法访问意图,只能访问结果。
这里存在两种有原则的逃生舱。 (i) 将控制输入与生产者选择的变量分离(例如,外生的积压证明或提交-披露 fee 分位数),或者 (ii) 固定控制器的敏感度(EIP-1559 风格)并接受较慢但稳健的自适应。我们的设计通过稀缺门控和残差,以及限制最坏情况损失的硬性保护措施来采用 (i)。
5. 对抗场景:控制器如何被博弈
5.1 方差锁定(价格发现 DoS)
一个联盟可以在 100% 和 60% 之间交替 gas 使用量(如在我们的 B3 场景中)。平均值为 80%,正好是目标值,但是方差 $\sigma_k^2$ 变得非常高。这驱动 $\etak \to 0$,将 base fee ($p{k+1} \approx p_k$) 冻结在远离真实清算价格的位置。该攻击是隐蔽的(没有空区块)并且有效:价格发现被禁用,而 fee 仍然被人为地抬高。这表现为我们的 KPI 中 price_gap_proxy(PartB_KPIs.csv: price_gap_proxy)的扩大(图 B3)。
5.2 欠填充 → 收割(短期挤压)
由于 ($-4 : +1$) 不对称性,一些空区块可以迅速降低 fee(每个区块最多 13.3%),而恢复速度很慢(每个区块最多 3.6%)。凭借 400 毫秒的 slot 和本地 mempool,一个卡特尔可以在几秒钟内执行此循环:抑制 fee,然后在诚实验证者做出反应之前包含他们自己的高小费交易。我们的 B4 场景显示了 ≈ +120 MON 的正 cartel net_tip_gain,证实了该漏洞的可盈利性(图 B4;PartB_KPIs.csv: net_tip_gain)。
5.3 架构放大器:本地 Mempool 和快速 Slot
虽然以太坊的大部分order flow现在是私有的(通过 MEV-Boost 和 proposer-builder 分离),但它的 base fee 机制仍然在约为 50% 的目标值周围保持固定增益和无记忆。交替不能崩溃学习率(因为没有学习率),并且 12 秒的区块时间让市场有时间对空区块进行套利。Monad 的设计凭借其自适应的 $\eta_k$ 和 400 毫秒的 slot,缺乏这些自然的平衡,使得操作既更容易又更有利可图。
6. 修复:一个对手无法steering的自适应控制器
为了打破反身性循环,该机制必须将其自适应性建立在生产者不容易控制或欺骗的信号上。我们的解决方案是分层防御。
6.1 来自最坏情况界限的 Minimax 保护措施
我们首先施加硬性限制以防止灾难性故障。
结果 2(通过保护措施消除反冻结和楔形)。 如果每个区块的指数被截断 $|\xi_k| = |\eta_k \Delta_k| \le \alpha$,并且学习率有一个下限 $\etak \ge \eta{\min}$,并且 $\eta{\min} \ge \alpha$,那么: (i) 在任何 $w$ 区块上,$b{k+w} \ge b_k e^{-\alpha w}$(没有方差锁定); (ii) 最大向下和向上对数速度相等,从而消除了快速向下/慢速向上楔形。 我们可以立即从限制指数的累积和中看到这一点。
我们选择一个价格发现horizon $w = 20$ 个区块(~8 秒),并容忍 $\delta = 0.3$(26%)的最大对数下降。这给出了 $\alpha = \delta/w = 0.015$。设置 $\eta_{\min} = \alpha$ 满足该条件。
为什么还要保持自适应性? 下限 $\eta_{\min}$ 确保了最坏情况下的恢复和对称速度;当稀缺性得到验证(通过门控)并且 残差 的分散性较低时,高于下限的自适应性仍然有价值,从而安全地减少了价格预言机的滞后,而无需重新打开方差锁定楔形。
6.2 稀缺性门控、定向自适应性
当经济信号确认低需求时,我们才允许方差来降低学习率。定义一个稀缺性门控:
$$ \phi_k = \mathbf{1}\Big[ B_k \leq \theta \;\land\; \mathrm{p90_bid}_k < (1+\delta_q)b_k \Big], $$
其中 $B_k$ 是一个积压代理。在本地 mempool 世界中,将 $B_k$ 定义为非本地稀缺性:来自至少两个不同的计划生产者可见的交易的 gas(通过重试或跨生产者 gossip),其age为 $\ge \tau$。我们通过 (a) 重试计数 $\ge 2$ 和 (b) age $\ge \tau$,gas 加权来近似它。当隐私允许时,fee 分位数的 VRF 采样提交-披露 在不暴露私有order flow的情况下加强了门控。
然后,我们使用 定向方差:永远不要抑制向上移动。 $$ \begin{aligned} \etak = \begin{cases} \max\left(\eta{\min}, \eta_{\max} \frac{\varepsilon}{\varepsilon + s_k}\right) & \text{如果 } g_k < T \text{ 且 } \phi_k=1 \text{ 且非 alt-alarm}k, \ \eta{\max} & \text{否则}. \end{cases} \end{aligned} $$
6.3 残差的稳健分散性,而不是原始利用率
领导者可以切换 $g_k$;他们无法廉价地欺骗外生稀缺性。我们对这些信号拟合一个小的在线预测器,并适应残差。 $$ \begin{aligned} \hat{g}_k = a_0 + a1 \hat{g}{k-1} + a2 \cdot \mathrm{sat}\left(\frac{B{k-1}-\theta}{\theta}\right) + a3 \cdot \frac{\mathrm{p90_bid}{k-1}}{b_{k-1}}, \quad r_k = g_k - \hat{g}_k. \end{aligned} $$
$$ \begin{aligned} \operatorname{sat}(x) = \max{-1,\ \min{x,\ 1}}. \end{aligned} $$
系数说明。 权重 $a_i$ 是小的正系数,可以启发式地设置(例如,$a_1 \in [0.5,0.8],\ a_2 \approx a_3 \approx 0.1$–$0.2$)或通过具有小学习率的简单最小二乘更新在线学习;通过饱和输入和将 $a_i$ 截断到一个紧凑的范围来确保稳定性。
我们使用最近残差的 中位数绝对偏差 (MAD) 来计算稳健的尺度 $s_k$: $$ sk = 1.4826 \cdot \mathrm{median}\left(|r{k-j} - \mathrm{median}(r)|\right)_{j=0}^{m-1}. $$
为什么这有效? 与积压和 fee 分位数对齐的诚实突发事件会被 $\hat{g}_k$ 预测,因此 $r_k$ 保持较小并且不会膨胀 $s_k$。与外生信号不相关的对抗性切换会产生大的残差,从而膨胀 $s_k$ 并否决阻尼。该预测器充当一个 战略噪声检测器。
6.4 交替否决和一个积压 Leg
我们添加了一个廉价的交替警报,以在怀疑方差锁定时否决阻尼。具体来说,在 20 个区块窗口上计算一个二进制序列 $u_k=\mathbf{1}{g_k \ge T}$ 上的 Wald–Wolfowitz 游程统计量,并且当标准化分数 $Z < -2.33$ ( $\alpha=0.01$) 时否决阻尼。最后,我们运行一个双腿控制器,该控制器永远不会以低于积压 justifies 的价格定价: $$ p_{k+1} = \max\left{ p_k + \tilde{\xi}_k, p_k + \eta^{(b)} \cdot \mathrm{sat}\left(\frac{B_k-\theta}{\theta}\right) \right}. $$ 这会将价格与领导者选择的 $g_k$ 分离。
7. 这是否关闭了漏洞?
一个自然的问题是,定向阻尼是否会打开一个新的漏洞:“pump-and-glide”(垃圾邮件来膨胀 $b$,然后在下降时收割)。使用我们的保护措施,这是无利可图的。
将 $b$ 提高一个因子 $R$ 的成本是至少为 $$ \frac{b0 L}{\eta{\max}} (R - 1) $$ 的 base-fee 燃烧的自我征税。(单位:$b0$ fee/gas,$L$ gas/区块,$\eta{\max}^{-1}$ 每个单位对数步长的区块;该产品下限了实现因子 $R$ 的累积燃烧量。) 下降受到 $\alpha$ 的限制,并受到稀缺性门控的否决;实现下降 $\delta$ 需要许多空区块,放弃小费/MEV。净预期价值为: $$ \text{EV} \lesssim \delta R b_0 Q - \frac{b0 L}{\eta{\max}}(R-1) - n{\downarrow} \cdot \text{tips}, \quad n{\downarrow}\ge \frac{\ln(1/(1-\delta))}{\min{4\eta_{\downarrow},\alpha}}. $$
数值示例: 假设 $b0 = 1000$ MON-gwei,$L = 10^9$ gas,$\eta{\max} = 1/28$,并且攻击者想要将 fee 翻倍 ($R=2$),然后收获 30% 的下降 ($\delta=0.3$)。燃烧成本为:
$$ \frac{1000 \times 10^9}{1/28} \times (2-1) = 28{,}000 \text{ MON}. $$ 潜在收益(假设他们可以在膨胀的 fee 下捕获 $Q = 10^8$ gas)为: $$ 0.3 \times 2 \times 1000 \times 10^8 = 60{,}000 \text{ MON}. $$
但是,使用 $\alpha = 0.015$ 实现 30% 的下降至少需要 $n_{\downarrow} \ge \ln(1/0.7)/0.015 \approx 24$ 个区块的被放弃的小费。以每个区块 ~500 MON 的小费计算,那就是 12,000 MON 的机会成本。净 EV:$60{,}000 - 28{,}000 - 12{,}000 = +20{,}000$ MON,看似有利可图。这个“账面利润”假设 (i) 当积压较高时,控制器会继续阻尼(它不会),(ii) 没有交替否决(它会),以及 (iii) 攻击者可以在诚实用户被定价出局的同时保持 $B_k$ 低(难以置信)。在门控和否决到位的情况下,我们的模拟将 EV 驱动到 $\le 0$,跨越现实的 $(R, \delta, Q)$。
因此,虽然一个简单的模型可能表明有利润,但我们的缓解措施引入的现实摩擦确保了任何“抽水和滑翔”的尝试在经济上都是不合理的。
8. 验证:从理论到模拟
我们的 notebook 端到端地验证了这些说法。
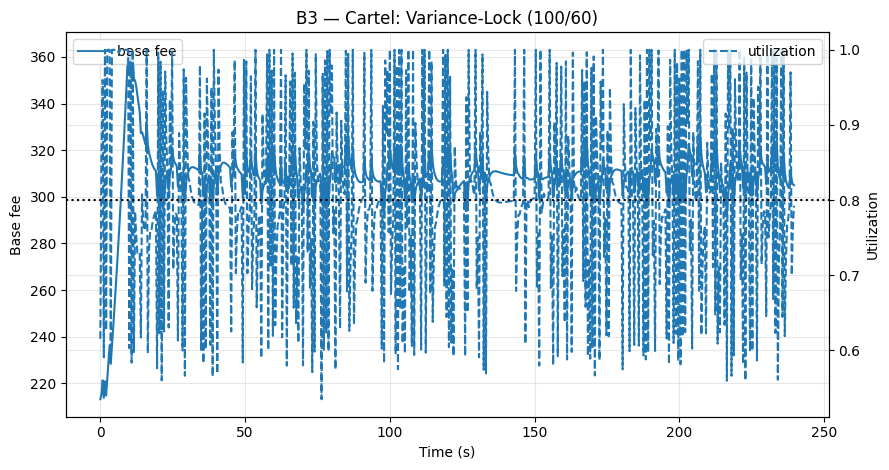
- 图 B3(方差锁定):$\eta_k \to 0$,一个平坦的 fee,以及一个高的
price_gap_proxy(PartB_KPIs.csv: price_gap_proxy)。
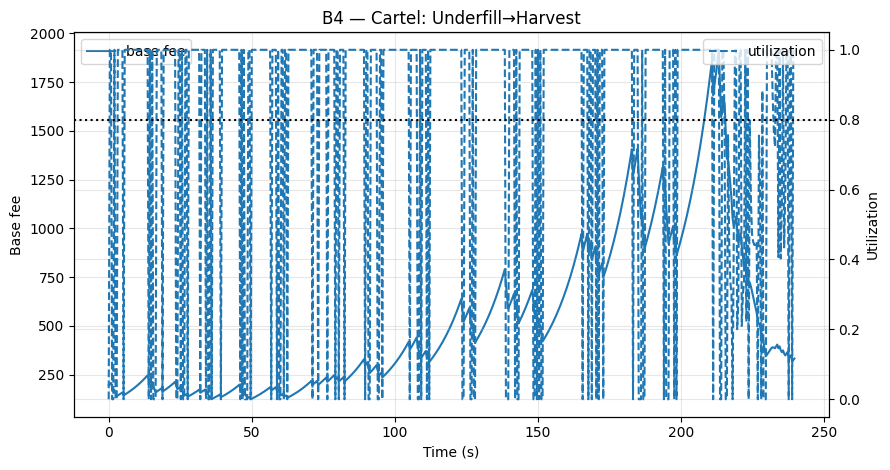
- 图 B4(欠填充→收割):急剧下降,缓慢恢复,以及正的
cartel net_tip_gain(≈ +120 MON;PartB_KPIs.csv: net_tip_gain,time_at_min_s)。
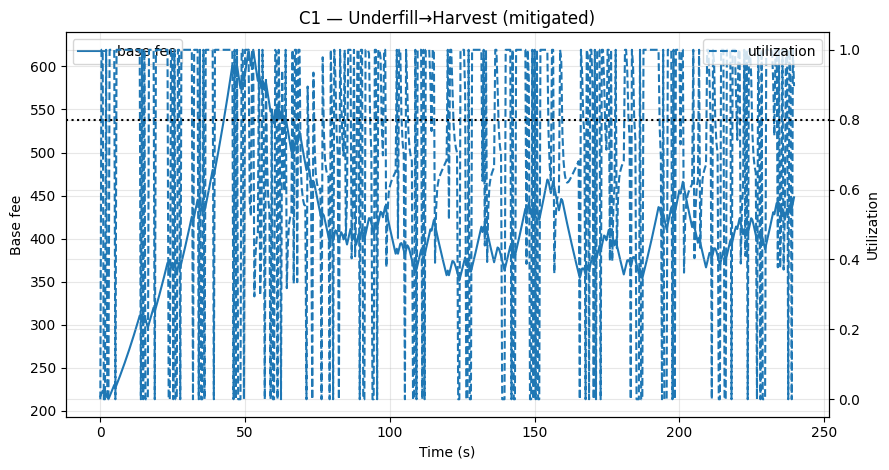
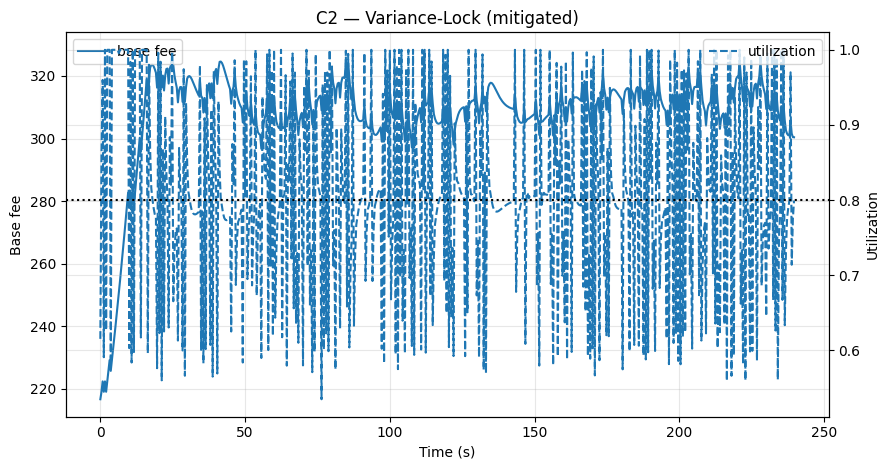
- 图 C1/C2(缓解措施):在应用修复程序后,
time_at_min_s ↓,base_log_span_p90 ↓,以及net_tip_gain → 0(Mitigations_KPIs.csv)。
所有图表和 CSV 都会写入 notebook 中的 /mnt/data/monad_unified_artifacts。
阅读指南: 实线 = base fee(左轴),虚线 = 利用率(右轴),点线 = 0.8 目标。
图 B3 – 方差锁定: 在 100/60% 利用率之间交替会加剧方差,崩溃 η,并使 fee 变平——价格发现停滞。
图 B4 – 欠填充→收割: 欠填充的突发事件会快速降低 fee;恢复速度很慢,为卡特尔暴露了一个利润窗口。
图 C1 – 欠填充→收割(缓解): 保护措施 + 稀缺性门控可防止 fee 自由落体/粘性;反弹很快,卡特尔收益消失。
图 C2 – 方差锁定(缓解): η-floor + 交替否决使 fee 尽管在高方差利用率的情况下仍能进行调整;没有冻结。
9. 部署配方(安全默认值)
对于希望实施此操作的工程师:
- Horizon:$w = 20$ 个区块(~8 秒)。
- 保护措施:$\alpha = \eta_{\min} = 0.015$。
- MAD 窗口:$m = 24$ 个区块。
- 积压门控:$\theta \approx 0.5L$,$\delta_q = 0.1$,具有非本地稀缺性定义(重试 ≥ 2;age ≥ $\tau$)。
- 积压 leg 增益:$\eta^{(b)} = \eta_{\max}$。
从 shadow 模式下的定向方差 + 队列覆盖 开始,并监控 time_at_min_s、price_gap_proxy、tip_pain_p95 和 net_tip_gain。
| 提议 | 影响 | 复杂性 | 优先级 |
|---|---|---|---|
| $\eta$ floor + 定向方差 | ★★★★★ | 低 | 关键 |
| 对称指数削波 | ★★★★★ | 低 | 关键 |
| 队列感知覆盖 | ★★★★ | 中等 | 高 |
| 全局 mempool / 需求预言机 | ★★★★★ | 高 | 战略性 |
10. 结论
自适应控制功能强大,但在对抗环境中,它必须适应对手无法廉价steering的信号。Monad 的原始规则将 $\eta_k$ 绑定到生产者选择的方差,并归一化偏差,以便向下移动淹没了向上移动。结果是可预测的:方差锁定冻结了价格发现,而欠填充→收割产生了私人收益。
我们的一小组有原则的更改,$\eta$ floor、由稀缺性门控的定向阻尼、对称指数界限和一个积压 leg,恢复了可预测性并消除了私人楔形,同时保持了“响应性但不抽搐”的精神。notebook 决定性地证明了这一点:这些修复减少了在 fee floor 的时间,缩小了 base-oracle 差距,并将卡特尔利润驱动到噪声。
更深层次的教训是: Monad 的设计是自适应控制方面的大胆实验,但它直接撞上了将机器学习与机制设计分开的反身性墙。我们提出的修复不是拆除那堵墙的方法,而是围绕它建造一个保护措施的方法。最安全的base fee 机制要么使用固定的、对称的规则,要么将自适应性建立在外生的、可验证的需求信号上。这不仅仅是 Monad 的一个补丁;它是在代理可以操作控制器输入信号的任何环境中构建健壮的自适应机制的蓝图。
- 原文链接: github.com/thogiti/thogi...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 2026 年智能合约审计的实际成本 93 浏览
- 【知识科普】| Gas费与交易安全:规避恶意合约资产消耗 88 浏览
- 宣布Trident Arena 108 浏览
- 区块链威胁建模 – ImmuneBytes 100 浏览
- 从 EVM 到 SVM:资深安全研究员给出的 2026 安全指南 126 浏览
- EVM 开发者在 Sui 上构建应用的心理模型 - 第二部分 423 浏览
- 【安全月报】| 1 月加密货币领域因安全事件损失超 4 亿美元 510 浏览
- 零时科技 || PGNLZ 攻击事件分析 523 浏览
- 如何用一年时间从零基础成为一名Web3安全审计师 830 浏览
- Timelock Guard - Optimism 99 浏览
- BlockThreat 周报 - 2026年第1周 1620 浏览
- 【知识科普】| 虚拟币网络传销 724 浏览

