智商低于200的人也能看懂的拉格朗日插值法

还记得那些需要连接点来形成图像的儿童绘画吗？ 经过这么多年，我们终于向你展示了一种作弊的方法。

插值是一种估计已知点之间值的方法。 这些点可以是例如温度测量值、图表中的点或仅是绘图中的点。

你可以连接点或进行插值

插值不是简单地连接点，而是为我们提供了一个通过这些点的公式。 在本文中，我们将解释如何使用数学家 约瑟夫-路易斯·拉格朗日 推广的一种方法来实现这一点。

快速定义

首先，让我们确定几个术语：

• 系数 是变量前面的数字。 例如，13、— 5 和 7 是函数 f(x) = 13x^4 — 5x + 7 中的系数（最后一个变量是隐式的 x^0）。
• 多项式 是由系数和 x 的幂组成的函数。 系数通常来自你知道的数字，例如整数或分数。
• 多项式的 阶数 是最高指数。 在我们之前的例子中，多项式的阶数是 4。

我们将在本文中通篇使用多项式，因为拉格朗日插值会生成多项式。

拉格朗日插值能给我们什么？

在一组点上执行插值会生成一个通过每个提供的点的多项式。

例如，假设我们有 (1,3) 和 (3,5) 这两个点。 我们稍后将详细介绍如何执行插值，但现在，这里有两个通过这些点的多项式：f(x) = x + 2 和 f(x) = x^3 — 12x + 14。

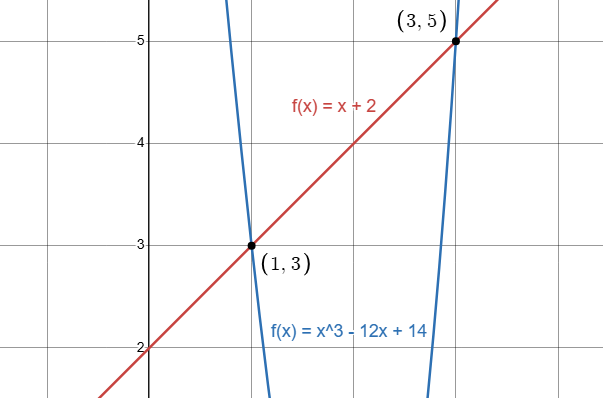
拉格朗日插值总是返回通过所有点的 最低可能阶数的唯一多项式。 例如，即使蓝色曲线也通过这些点，拉格朗日也会返回红线，因为它具有最小的阶数。

通常，最小阶数比点数少一。 然而，在极少数情况下，这些点可能会完全对齐，从而允许使用较低阶的多项式。 例如，在我们之前的示例中，在 (2,4) 处添加第三个点仍然允许同一条红线插值所有点。

单点插值

考虑点 (3,5)。 通过此点的最小阶数的多项式是什么？

对于我们的点，我们知道 x = 3 得到 y = 5。 由于我们只有一个点，因此没有关于多项式在其他地方应如何表现的信息。 最低阶的选择是不随 x 变化的常数多项式：f(x) = 5。

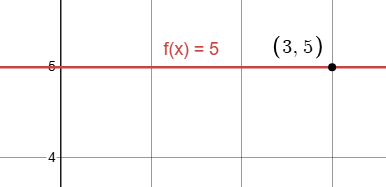
一旦我们有更多的点，事情就会变得更有趣（也更具挑战性）。

没有拉格朗日的两点

让我们再次使用点 (1,3) 和 (3,5)。

我们知道我们可以通过绘制一条直线来连接两个点。 我们如何获得对应于这条线的多项式？

一条线是 1 阶多项式：f(x) = ax + b，其中 a 告诉我们当 x（斜率）增加时线升高得有多快，而 b 是当 x = 0 时多项式的结果值。

要找到斜率 a：

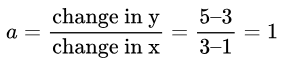
由于我们还不知道 b，我们可以通过要求该线通过我们的一个点来解决它。 让我们将 (1,3) 和 a 的值代入我们的函数 f(x) = ax + b：

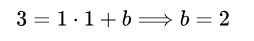
通过代入 a 和 b，我们得到最终多项式 f(x) = x + 2。

拉格朗日方法

如果我们添加更多的点，同样的推理也适用，但计算很快就会变得混乱。 拉格朗日插值为我们提供了一种更简洁的处理方式。

基本思想很简单：

1. 单独关注每个点。 对于每个点，创建一个中间多项式，在该点等于 1，在所有其他点等于 0。 我们将这些多项式称为 L_i，其中 i 是点的索引。
2. 按 y 值加权。 将每个中间多项式乘以该点对应的 y 值。 我们将这些多项式称为 P_i，其中 i 再次是点的索引。
3. 组合多项式。 将所有这些多项式加在一起以获得最终多项式，该多项式通过所有点。

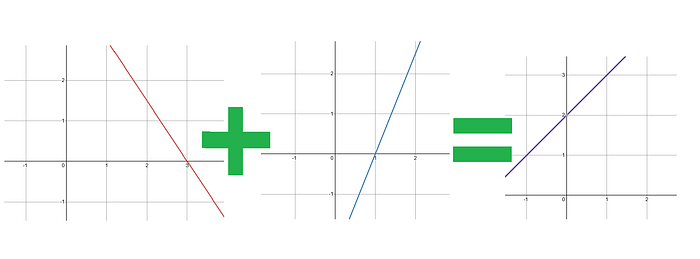
我们将在下面详细介绍

拉格朗日适用于两点

让我们通过一个具体的例子来完成这些步骤。 我们将再次使用点 (1,3) 和 (3,5)。

步骤 1：单独关注每个点

首先，让我们为点 (1,3) 创建中间多项式。 我们想要一个多项式，它：

1. 在目标点 x = 1 处为 1。
2. 在所有其他点都是 0。 我们只有一个其他点：(3,5)。 所以多项式需要在 x = 3 处为 0。

从第二个要求开始，我们从一个在点 x = 3 处等于 0 的项开始。 最简单的选择是 x — 3。 在 x = 3 处，该项为 3 — 3 = 0，因此符合我们的要求。

为了满足第一个要求，我们需要调整 x - 3，使其在 x = 1 处等于 1。 在 x = 1 处，项 x - 3 为 1 – 3 = -2。 为了使 -2 等于 1，我们将其除以 -2：-2 / -2 = 1。 因此，我们的第一个中间多项式变为：

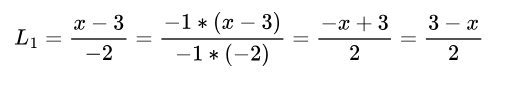
以及相同的多项式，在视觉上：

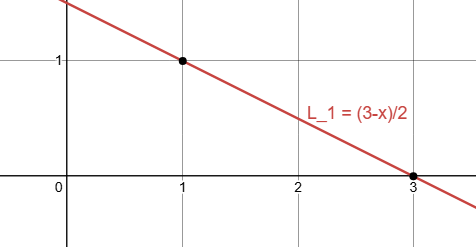
该多项式满足我们的要求：当 x=1 时为 1，当 x=3 时为 0

我们可以使用相同的逻辑来计算第二个中间多项式：

1. 找到一个在点 x = 1 处等于 0 的项。 最简单的选择是 x - 1。
2. 调整 x — 1，使其在 x = 3 处等于 1。 计算 3 — 1 = 2。 因此，为了使 2 等于 1，将其除以 2。

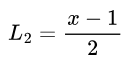
在视觉上：

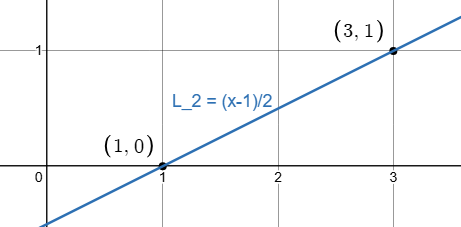
该多项式满足我们的要求：当 x=3 时为 1，当 x=1 时为 0

步骤 2：按 y 值加权

如果我们按原样组合中间多项式，则每个点的 y 值将仅为 1。 我们的点具有不同的 y 值。 为了解决这个问题，我们用其点的实际 y 值来加权每个中间多项式。

请记住，我们的点是 (1,3) 和 (3,5)。

为了加权第一个中间多项式，我们将其乘以该点的 y 值：

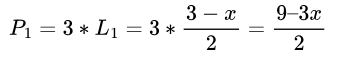
第二个：

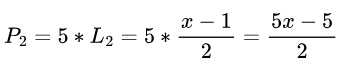
步骤 3：组合多项式

现在我们有了独立的多项式，每个多项式都达到其对应的点，并且在其他点均为零。 为了获得最终结果，我们只需将这些多项式相加：

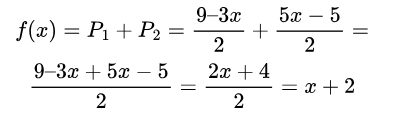
我们得到与没有拉格朗日相同的结果。 在视觉上，构造看起来像这样：

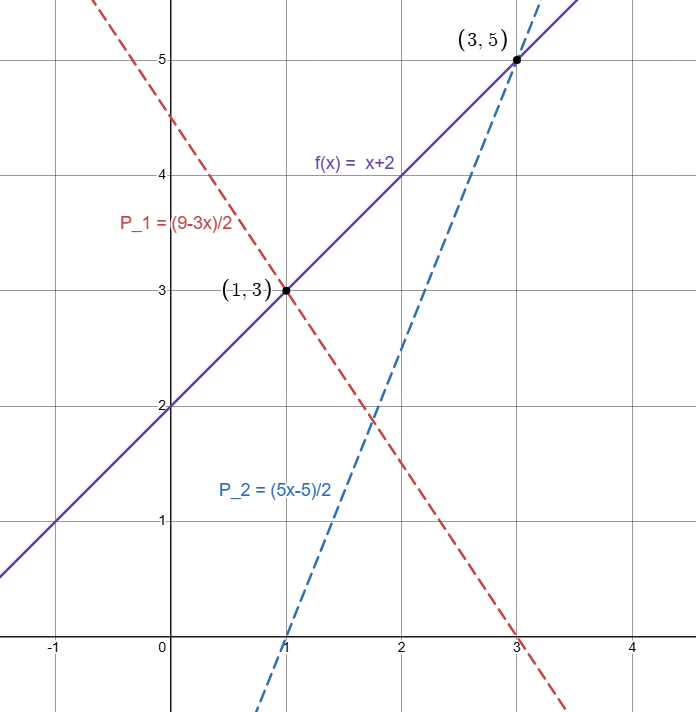
红色 + 蓝色 = 紫色

拉格朗日适用于三个点

相同的逻辑适用于任意数量的点。

让我们添加第三个点。 我们的点是：(1,3)、(3,5) 和 (2,6)。

步骤 1：单独关注每个点

对于点 (1,3)，我们想要一个中间多项式，它：

1. 当 x = 1 时为 1。
2. 当 x = 3 和 x = 2 时为 0。

再次从第二个要求开始，我们可以看到最简单的选择是 (x — 3)(x - 2)。 对于该项，如果 x = 3 或 x = 2，则结果为零（对于任何一个值，其中一个边变为零，使整个乘法为零）。

为了满足第一个要求，让我们调整 (x — 3)(x - 2)，使其在 x=1 处等于 1。 在 x=1 处，项 (x - 3)(x - 2) 为 (1 – 3)(1 – 2) = 2。

按照相同的逻辑，我们可以构造所有中间多项式：

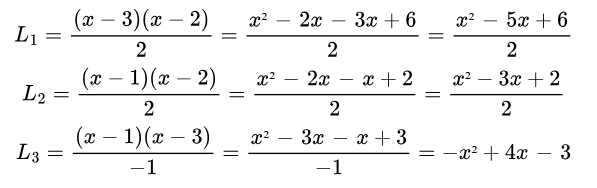
步骤 2：按 y 值加权

加权多项式：

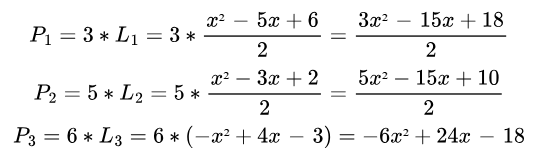
步骤 3：组合多项式

最后，我们对多项式求和：

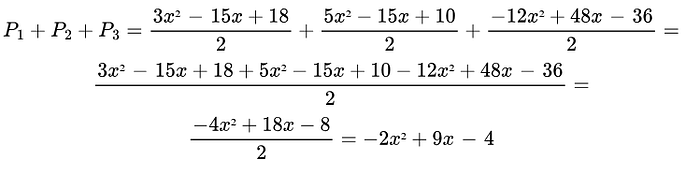
这是相同的过程，在视觉上：

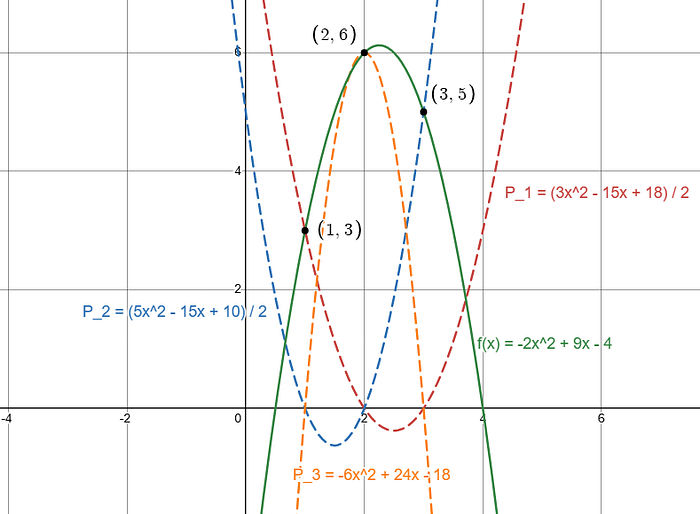
红色 + 蓝色 + 橙色 = 绿色

但是为什么？

玩点和线很有趣，但这有什么用呢？

这些点不需要只是图表上的点，它们可以代表真实的数据。 插值使我们能够将分散的值转化为完整的画面，这种想法有很多强大的用途：

• 数据恢复：如果你丢失了一些数据点，可以对它们的数据进行插值。 例如，可以插值丢失的音频数据。
• 零知识证明：大部分计算都表示为多项式。 验证者不验证每个点，而只从多项式中抽样点。 感谢 Schwartz-Zippel 引理 和插值，通过只知道几个点就可以很容易地比较多项式。
• 图形：计算机图形通常依赖于插值来生成点之间的平滑运动。

我们并不孤单

拉格朗日插值并不是唯一酷炫的方法：还存在其他插值技术。

事实上，它通常不是插值点的最有效方法。 但它 是 最容易理解和使用的方法之一，这使得它非常适合学习和教学。

对于实际应用，通常改用称为 快速傅里叶变换 的方法。

结论

好的，这对儿童绘画来说不是超级有用。 但当你需要找到一个通过给定点集的多项式时，它是一种强大的方法。

核心思想保持不变，无论你添加多少个点：构建简单的中间多项式，对其进行加权，然后将它们加在一起。 你拥有的点越多，细节上的工作就越多，但原理永远不会改变。

这就是使拉格朗日插值有价值的原因：它易于理解，保证给出唯一的结果，并且易于在代码中实现。

感谢

感谢 Frank Mangone 审阅了本文的一个版本，并确保其有意义！

关于作者

我是一名 ZK 和 EVM 自由职业者。 我主要从事 零知识主题和生态系统 的开发和写作。 想聊聊吗？ 联系我！

• 原文链接： medium.com/@laurippelton...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～