Arbitrum约束阶梯 Gas定价器的控制理论视角

Arbitrum 的帖子 建议用多约束版本替换单一的指数 “积压” 定价器，并且，进一步，用一个约束阶梯在长时程和短时程资源约束之间插入中间时间尺度[^1]。短时程约束（防止执行器落后）应快速响应费用调整，而长时程约束（控制状态增长）应缓慢响应。他们的帖子给出了积压更新和定价的具体公式，并通过一个实际例子说明了阶梯的必要性。我在这里的博客中采用了这些定义，并将它们重新描述成了控制理论中的标准反馈控制器，然后用显式假设、一致的符号和离散时间论证分析了闭环。目的是展示为什么约束阶梯能够解决稳定性/性能之间的紧张关系，以及如何校准它们。

基线定价模型、变量和符号

时间原则上是连续的，但在这个模型中，我们以 $\Delta t$ 秒的离散步长进行分析（例如，$\Delta t=1 s$）。设 $T>0$ 表示每秒所需的平均 gas 使用量（Mgas/s）。设 $A>0$ 是以秒为单位的调整时间，即控制器的耐心。设 $P_{\min}>0$ 是价格下限（gwei）。在时间 $t$，定价器观察实际 gas 使用量 $\lambda_t$（Mgas/s）并维护一个积压 $B_t$（Mgas·s），该积压集成了超过目标的过度消耗。更新规则是

$$B_{t+\Delta t}=\max{0,B_t+(\lambda_t-T) \Delta t},$$

并且报价的 L2 计算价格为

$$ Pt=P{\min}\exp\big(B_t/(AT)\big). $$

通过对数价格状态重新参数化价格

$$ x_t {=} \log\frac{Pt}{P{\min}}=\frac{B_t}{AT}. $$

因为 $Pt=P{\min}e^{x_t}$，所以 $x_t$ 的更新变为

$$ x_{t+\Delta t}=\max{0,x_t+k(\lambda_t-T)},\qquad k = \frac{\Delta t}{AT}. $$

这是一个关于误差 $e_t=\lambdat-T$ 的纯积分控制器，带有一个钳位，因此价格不会低于 $P{\min}$。

为什么离散时间是正确的抽象

区块链执行定期对需求进行采样并更新费用，即排序器批处理间隔或区块时间。设 $\Delta t$ 表示此周期。测量的使用量 $\lambda_t$ 是 $[t,t+\Delta t)$ 上的平均值，并且在时间 $t$ 报出的费用应用于 $t+\Delta t$。在这种时序下，离散更新

$$ B_{t+\Delta t}=\max{0,B_t+(\lambda_t-T)\Delta t} $$

与连续积压积分的 黎曼和 类似物相匹配，并且线性化特征值的离散稳定性条件 $ \vert a \vert <1$ 是块同步控制的正确标准。选择 $\Delta t$ 等于排序器的决策节奏，可以使模型与实现保持一致。

分析的假设

对于小信号分析，将已实现的使用量建模为 $\lambda_t \approx \Lambda(Pt)$，直到出现短暂的噪声，其中 $\Lambda:(0,\infty)\to[0,\infty)$ 是连续的，并且在任何紧区间 $[P{\min},\bar P]$ 上严格递减。钳位在工作点 $x_t>0$ 处不活动，并且驱动/测量延迟不会太大，以至于使 $\Delta t$ 间隔模型无效；“实质延迟” 在下面量化。这些是围绕平衡点的离散时间积分控制的标准。

用 $Pt=P{\min}e^{x_t}$ 替换 $\lambda_t \approx \Lambda(P_t)$，从而闭环：

$$ x_{t+\Delta t}=\max{0,xt+k[\Lambda(P{\min}e^{x_t})-T]}. $$

稳态 $x^*>0$ 满足 $\Lambda(P^*)=T$，其中 $P^*=P_{\min}e^{x^*}$。

局部稳定性和 “足够耐心” 条件

对于具有非活动钳位的小偏差 $\delta x_t=x_t-x^*$ 进行线性化，得到

$$ \delta x_{t+\Delta t}\approx a\delta xt,\qquad a=1+k\Lambda'(P^*)\frac{\partial P}{\partial x}\Big|{x^*} =1+k\Lambda'(P^*)P^*. $$

由于需求随着价格的降低而降低，因此 $\Lambda'(P^*)<0$。离散时间稳定性条件 $\vert a \vert<1$ 变为

$$ -2<k\Lambda'(P^*)P^*<0 \Longleftrightarrow 0<\frac{\Delta t}{AT} \vert \Lambda'(P^*) \vert P^*<2. $$

这是足够耐心不等式。小的 $A$（不耐心）会增加 $k$，并将特征值推向 $-1$ 并导致振荡；非常大的 $A$ 会导致响应迟缓。不等式支持根据在 $P^*$ 处测得的弹性 $ \vert \Lambda'(P^*) \vert $ 对 $A$ 进行数据驱动的校准。

为什么单一约束对无害的突发流量反应过度

单一约束方法使用一个 $(T,A)$ 来同时保护秒级的执行和天级的状态增长。保护执行器会将你引向小的 $A$，然后小的 $A$ 会应用于所有偏差，包括远低于执行风险的良性十分钟突发流量。在线性模型中，小的 $A$ 会增加 $k$，因此即使是小的瞬态误差 $(\lambdat-T)$ 也会迅速地增加积分。然后，指数 $P=P{\min}e^x$ 会将其放大为大的价格跳跃。当只有一个积分状态存在时，这是时间尺度和增益之间的结构耦合。

多约束定价、雅可比矩阵和阶梯

在多约束阶梯模型中，我们并行跟踪多个积压：

$$ B{i,t+\Delta t}=\max{0,B{i,t}+(\lambda_t-T_i)\Delta t},\qquad xt=\sum{i=0}^{K}\frac{B_{i,t}}{A_iT_i},\qquad Pt=P{\min}e^{x_t}. $$

每个阶梯 $i$ 都有一个目标 $T_i$ 和耐心 $A_i$。在内部平衡 $x^*>0$ 时，

$$ \frac{\partial x_{t+\Delta t}}{\partial \mathbf{B}t} =\Big[\tfrac{1}{A_0T_0},\dots,\tfrac{1}{A_KT_K}\Big],\qquad \frac{\partial \mathbf{B}{t+\Delta t}}{\partial x_t} =\mathbf{1}\Lambda'(P^*)P^*\Delta t, $$

因此闭环特征值为

$$ a=1+\Big(\sum_{i\in\mathcal{A}}\frac{\Delta t}{A_iT_i}\Big)\Lambda'(P^*)P^*, $$

其中 $\mathcal{A}$ 是其积压处于活动状态的阶梯的集合。用有效积分增益 $k{\mathrm{eff}}=\sum{i\in\mathcal{A}}\Delta t/(A_iTi)$ 替换 $k$。当负载较低时，只有慢速阶梯会影响 $k{\mathrm{eff}}$，并且循环是耐心的；随着负载接近风险更高的状态，快速阶梯会启动并且 $k_{\mathrm{eff}}$ 会平稳增加。天级状态阶梯和 100 秒执行阶梯之间的几何间距会产生平稳的增益时间表。Arbitrum 研究帖子[^1] 通过具体的参数和 30 Mgas/s 的突发示例阐述了这种结构和阶梯的直觉。

将每个阶梯视为具有泄漏率 $T_i$ 的 “泄漏” 积分器：如果需求低于目标，则积压会以每秒 $T_i$ 的速度耗尽。用频率术语来说，多约束控制器是不同截止频率下低通滤波器的总和；短脉冲主要激发最快的阶梯，并在它们冲击慢速积压之前消散。这与主动队列管理（PIE[^2]、CoDel^4）并行，在主动队列管理中，不同的时间常数可以抑制突发性而不会引起振荡；用 “执行松弛” 替换 “队列延迟”，类比仍然成立（PIE：RFC 8033[^3]，CoDel^4：ACM 队列）。

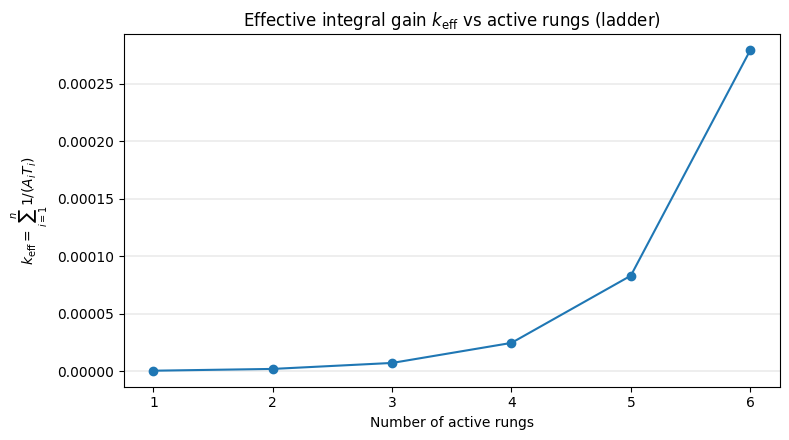
图 1：$k_{\mathrm{eff}}$ 与活动阶梯的数量

增益时间表的直觉

这里一个有用的类比是汽车的变速箱。在良性负载下，阶梯以高档运行：只有长时程阶梯处于活动状态，因此控制器是耐心的并且是高效的。随着负载的增加，该机制通过中间阶梯降档，平稳地增加有效增益；只有当执行处于危险之中时，最快的阶梯才会接管，即具有紧急扭矩的低档。在几何间距下，档位变化是逐渐的。我们现在回到正式的校准，以在特征值中看到此时间表。

实践中的间距

几何间距是一个很好的默认值。Arbitrum 模拟以及我们自己的分析中的直接复制表明，在快速端附近更密集的放置会减少对短脉冲的过度反应，同时保持对短时程的保护；一个实用的规则是将约 $60%$ 的阶梯放置在时间尺度频谱的前三分之一（例如，$50$–$300$ 秒）中，并将其余的阶梯以对数方式向下分布到慢速时程。对于受状态增长约束的链，几乎在整个范围内以对数方式均匀放置阶梯。将每个中间阶梯放置在其相邻阶梯的时间常数的调和平均值附近，以均衡对 $\sum_i 1/(A_iT_i)$ 的增量贡献；与单独的几何间距相比，这均衡了每个阶梯对有效增益的边际贡献，并产生了更平稳的切换。

延迟、阻尼和一个具体的安全边际

上面的稳定性不等式假定需求在一个 $\Delta t$ 间隔内做出反应。在实践中，存在驱动/测量延迟：用户、机器人和排序器会滞后响应，并且 $\lambda_t$ 是执行器松弛的不完善代理。一种保守的补救措施是保持稳定因子

$$ \Phi = \Big(\sum_{i\in\mathcal{A}}\frac{\Delta t}{A_iT_i}\Big) \vert \Lambda'(P^*) \vert P^* $$

低于一个严格的边际 $\rho<2$。当延迟超过两到三个采样间隔时（例如，对于具有约 $2$–$4$ 秒批处理时间的 rollup，为 $2$–$3$ 个区块），选择 $\rho\approx 1$。

执行器松弛信号

设 $S_t$ 表示执行器松弛（在执行器落后于排序器之前的毫秒级裕量）。为了避免噪声放大，在反转之前，使用一个短窗口（例如，3 样本 EMA）平滑 $S_t$。定义反向松弛压力

$$ \sigma_t=\max\Big(0,\frac{1}{St}-\frac{1}{S{\mathrm{safe}}}\Big), $$

其中 $S_{\mathrm{safe}}$ 是目标松弛（例如，$100$ 毫秒）。最快的阶梯应该调节 $\sigma_t$，而不是原始的 $\lambda_t$，因为 $\sigma_t$ 测量与执行失败的接近程度，并且更难通过表面批处理来操纵。

一种补充的补救措施是在最快的阶梯上添加一个小的比例项 (PI)：

$$ xt=\sum{i}\frac{B_{i,t}}{A_iT_i}+K_P[,\sigmat-\sigma{\mathrm{target}},],\qquad \sigma_{\mathrm{target}}=0. $$

比例项会增加延迟下的阻尼；积分项保持零稳态误差。如果 $S_t$ 嘈杂，请在比例项之前使用一个短 EMA（2-3 个样本）。

对抗性时序和博弈

排序器可以成批处理交易以塑造近期的拥堵，并且用户可以抢先预期价格变动。阶梯有所帮助，因为只有那些时间范围确实被违反的阶梯才会累积积压；短暂的成批处理主要激发快速阶梯并迅速耗尽。在这种情况下，两种强化措施是实用的：从执行器松弛（或其反向）而不是原始拥堵计算顶部阶梯信号，并在更新慢速阶梯之前将一个短 EMA 应用于 $\lambda_t$，以便只有持续的压力才会累积在长时程上。这些保留了我们上面讨论的数学原理，并细化了每个阶梯的测量。

防积分饱和、死区、速率限制和硬限制

如果由于策略原因限制了价格，或者区块拥堵达到硬性最大值，则工厂会饱和，而积分状态可能会饱和，从而在事件发生后导致不必要的高价格。反向计算防积分饱和会按照请求的对数价格 $x{\mathrm{raw}}$ 和强制的 $x{\mathrm{eff}}$ 之间的差成比例地消耗积分状态，因此积压反映了强制的 $x=\log(P/P_{\min})$ 并迅速解除。测量噪声和排序器时序可能会导致 $(\lambda_t-T)$ 中的快速符号翻转；对每次对数 $P$ 的变化施加一个小死区 $\vert \lambdat-T\vert<\epsilon$ 和一个边界 $\vert x{t+\Delta t}-xt \vert \le r{\max}$，可以在不改变稳态行为的情况下提高鲁棒性。

低利用率状态

当 $\lambda_t \ll \min_i Ti$ 持续一段时间时，所有积压都会耗尽为零，并且价格会收敛到 $P{\min}$。阶梯结构优雅地恢复：快速阶梯首先清空，然后逐渐清空速度较慢的阶梯，这避免了从安静期重新启动时发生振荡。在长时间的低利用率期间，由于测量噪声，最慢的阶梯可能永远不会完全耗尽；在实践中，当 $\lambda_t < 0.5 \times \min_i T_i$ 超过一小时时，对最慢的积压施加一个微小的负偏差或执行定期重置。

在硬 gas 限制下，交互很简单：当上限绑定时，执行器饱和，防积分饱和会阻止漂移，并且一旦压力减轻，价格会迅速恢复到运行状态。

实现占用空间和链上可行性

对于 $K{+}1$ 个阶梯，控制器会维护 $K{+}1$ 个标量 $B_i$ 并每 $\Delta t$ 更新一次。每次更新的工作量为 $O(K)$：相加、每个阶梯一个钳位、一个点积 $x=\sum_i B_i/(A_iTi)$ 和一个指数 $P=P{\min}e^x$。在排序器上，对于 $K\le 8$，此成本可以忽略不计。如果任何费用计算必须在链上执行，则在链下预先计算 $x$（或 $P$）并提交带有范围证明或有界更新的 $x$；合约会强制执行上限、速率限制和参数完整性。参数开销很少更新且可审计，为 $2(K{+}1)$ 个数字 $(T_i,A_i)$。

一个具体的数值校准

设 $\Delta t=1$ s， $T=25$ Mgas/s， $P^*=0.30$ gwei，并且根据经验 $\vert \Lambda'(P^*) \vert \approx 60$ (Mgas/s)/gwei。对于单约束定价器，

$$ a_{\text{single}} =1+\frac{\Delta t}{AT}\Lambda'(P^*)P^* =1-\frac{18}{25A}. $$

当 $A=0.5$ s 时，$a=-0.44$（稳定但欠阻尼）。当 $A=2.0$ s 时，$a=0.64$（阻尼良好，速度较慢）。现在考虑一个三阶梯阶梯，其中 $(T_i,A_i)\in{(25,86400),(37.5,600),(50,102)}$。完全激活时的有效增益为

$$ k_{\mathrm{eff}}=\sum_i\frac{1}{A_iT_i} \approx \frac{1}{25\cdot 86400}+\frac{1}{37.5\cdot 600}+\frac{1}{50\cdot 102} \approx 0.00000046+0.000044+0.000196 \approx 0.000240, $$

所以

$$ a{\text{ladder}}=1+(\Delta t)k{\mathrm{eff}}\Lambda'(P^*)P^* =1-0.000240\cdot 18 \approx 0.996 $$

当所有阶梯都处于活动状态时。对于 10 分钟 30 Mgas/s 的突发，只有快速阶梯会累积积压；慢速阶梯保持接近于零，因此 $k_{\mathrm{eff}}\approx 1/(50\cdot 102)\approx 0.000196$，并且 $a\approx 1-0.000196\cdot 18 \approx 0.9965$，一个小的、阻尼良好的偏差。只有当多个时程绑定时，稳定裕量 $\Phi=\big(\sum_i 1/(A_iT_i)\big) \vert \Lambda'(P^*) \vert P^*$ 才会增长。

裕量的敏感度

稳定裕量 $\Phi=\big(\sum_i 1/(A_iT_i)\big) \vert \Lambda'(P^*) \vert P^*$ 对最快的阶梯比对最慢的阶梯更敏感。顶部阶梯的耐心 $A_K$ 变化 10% 会使 $\Phi$ 大致移动 10%，而天级 $A_0$ 变化 10% 通常会使 $\Phi$ 移动不到 0.1%（它对 $\sum_i 1/(A_iT_i)$ 的贡献很小）。这支持对快速阶梯的保守校准和对慢速阶梯的更积极的调整。这指导了迁移中 $A_K$ 的保守默认值。

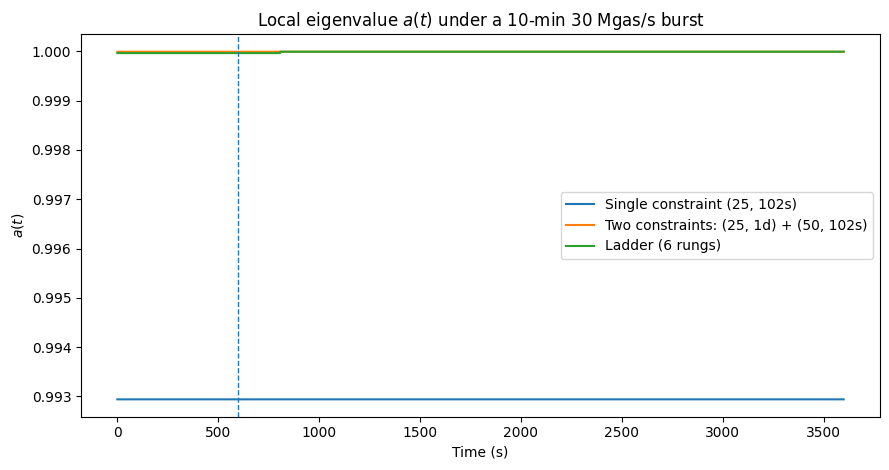
图 2：在 10 分钟 30 Mgas/s 的突发下的局部特征值 $a(t)$

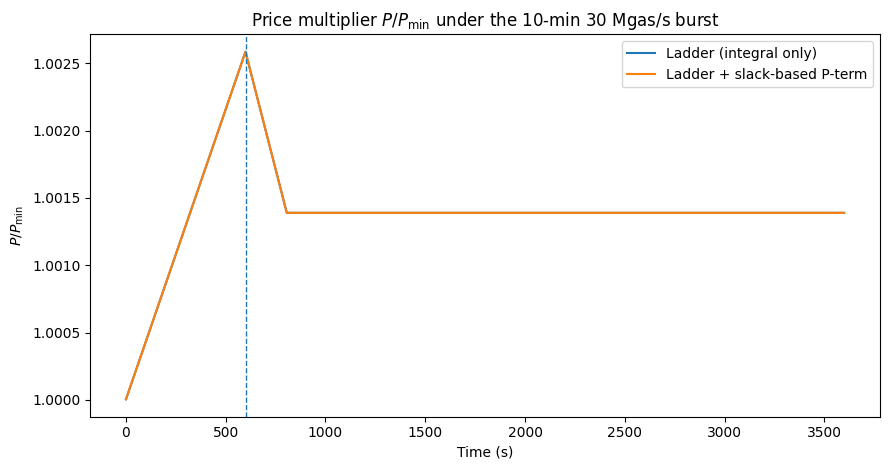
图 3：在最快的阶梯上使用和不使用基于松弛的 $KP$ 的价格乘数 $P/P{\min}$

这个 python Jupyter notebook 重现了上面的模拟[^5]。

通过风险定价阶梯进行经济校准

为了将价格与尾部风险对齐，借鉴电力市场的运行储备需求曲线 想法：一个预先指定的稀缺性附加项，随着储备的减少而增加[^3]。RTO/ISO 市场（PJM、ERCOT、MISO）中的 ORDC 实现表明，可以如何将阶梯式或倾斜式稀缺性附加项校准为 失负荷概率 和 失负荷价值；当 “储备” 是执行器松弛和状态裕量时，同样的逻辑也适用于此处。

对于阶梯 $i$，定义一个稀缺性项

$$ \Delta \log P_i(B_i)=\alpha_i,\mathrm{LoLP}_i(B_i), $$

其中 $\mathrm{LoLP}*i$ 是失负荷概率（在其时程内违反约束 $i$ 的概率），从执行器遥测（滞后分布、同步追赶率、状态数据库压缩债务）或压力测试中估计得出。比例 $\alpha_i$ 是执行/状态损失价值 (VLOE/VLOS)。然后设置

$$ \log P=\log P_{\min}+\sum_i \frac{B_i}{A_iT_i}+\sum_i \alpha_i\mathrm{LoLP}_i(B_i). $$

线性积压项继续调整目标；ORDC 风格的附加项对罕见事件进行定价。（有关 ORDC 公式及其在稀缺性定价中的作用的背景信息，请参阅 FERC 工作人员摘要和 Hogan 的入门读物。）

在备选方案中定位此模型

约束阶梯不同于多维定价（计算、数据、带宽的不同价格）、基于预测的控制器（预测需求并预先调整 $P$）和市场微观结构（区块空间的拍卖或 CFMM）。阶梯保持单个标量价格，同时通过控制器状态恢复多时程行为，从而保持可解释性和稳定性保证。它们可以与多维收费或简单预测相结合；阶梯解决了单约束积分器无法解决的时程耦合问题。

我之前在两篇文章中探讨过相关想法：关于多维定价和关于 AI 辅助机制设计。这些观点与约束阶梯互补：多维定价解开了特定于资源的稀缺性，而 AI 方法可以帮助调整参数或设计更丰富的微观结构，并且两者都可以与阶梯结合使用以保持稳定、可审计的时程控制。

迁移策略

考虑到费用动态的外部性，应该分阶段进行更改。以下是一些关于如何处理此问题的想法。

以影子模式启动：在链下计算梯形价格，并在实时单约束价格旁边记录 $x_{\text{ladder}}$ 和每个梯级的贡献。然后在相关的运行点拟合 $ \vert \Lambda'(P) \vert $ 并测量延迟后冻结参数。继续进行渐进式激活：首先启用顶部梯级，随着时间的推移添加中间梯级，同时监控执行器松弛、积压直方图和价格半衰期。保持防积分饱和、死区和每次 $\Delta\log P$ 上限作为保护措施。

结束语

Arbitrum 的积压定价器 是一个离散时间积分控制器，用于将需求过程调整到目标速率 $T$。当其积分增益满足与需求的局部斜率和采样间隔相关的清晰不等式时，单约束版本是稳定的，但如果将其时间常数设置为保护短时程资源，则它往往会对短暂的、无害的突发反应过度。多约束定价器，特别是具有长时程和短时程之间的约束阶梯，允许有效增益取决于哪些约束正在绑定。通过对延迟裕度 $A_i$ 进行经验校准、在最快的阶梯上添加小的比例项以进行阻尼以及标准的防积分饱和、死区和速率限制，该机制具有良好的阻尼和可审计性。

参考文献

[^1]: 多约束定价 - Arbitrum Research

[^2]: RFC 8033 - 比例积分控制器增强 (PIE)

[^3]: FERC - 解决能源和辅助服务市场改革

[^5]: Arbitrum 约束梯形定价器的模拟 - 控制理论模型

• 原文链接： github.com/thogiti/thogi...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～