解构 Bulletproofs 的魔力：SageMath 深度解析

零知识证明以在微小的证明中封装惊人的安全性而闻名，但它们实际上是如何实现的呢？

秘密在于内积参数 (IPA)，这是 Bulletproofs 背后的数学引擎。

在这篇文章中，我们将逐步剖析它，看看它是如何真正工作的，并配有你可以自己玩的、可运行的 SageMath 代码，因为没有什么比代码更能建立直觉了。

这是关于 IPA/Bulletproof 协议的一个小系列的第二部分。如果你错过了第一部分，请从那里开始了解全局：Bulletproofs/IPA 协议的高级直觉。

在这里，我们将深入研究协议的核心，并揭示使整个协议得以实现的神秘的 L 和 R “交叉项”。

如果你好奇，这些脚本在 GitHub 上。

但让我们先热身一下。我们将从最基本的要素开始：没有承诺，没有椭圆曲线，没有零知识魔法。只有向量和内积。一旦这幅图清晰了，添加密码学魔法（Pedersen 承诺）就会感觉更加自然。

内积参数，第一步：尚未承诺

我们从两个向量 $\vec{a}$ 和 $\vec{b}$ 开始。证明者想要说服验证者，它们的内积是某个值 c

$\langle \vec{a}, \vec{b} \rangle = c$

当然，如果我们不隐藏任何东西，证明者可以直接将这两个向量发送给验证者。简单，但无聊 🥱。真正的挑战是：

• 发送更少的数据
• 使验证更快

这就是折叠的用武之地。

折叠向量以压缩证明

我们已经在第一部分中看到了折叠：

• 我们将每个向量分成两半
• 然后使用随机线性组合将它们压缩成一个新的、更短的向量

每一轮都将长度减半，直到我们只剩下一个条目。

为了使它顺利工作，我们需要：

• $\vec{a}$ 和 $\vec{b}$ 具有相同的长度
• 该长度是 2 的幂（如果不是，我们可以用零来填充）

假设我们有 $\vec{a} = (a_1, a_2, a_3, a_4)$

我们把它分开：

$a_L = (a_1 a_2), a_R = (a_3 a_4)$

验证者发送一个随机挑战 x（或者我们通过 Fiat-Shamir 获得它）。然后我们这样折叠：

$\vec{a'} = x \cdot a_L + x^{-1} \cdot a_R$

我们称 $\vec{a'}$ 为向量 $\vec{a}$ 的折叠版本。

我们用 $x$ 和 $x^{-1}$ 计算它的方式将使各项相互抵消，这是我们的证明如何工作的关键。

让我们看看它在 Sage 中是什么样子的：

def fold(vec, val):
    assert len(vec) % 2 == 0

    half = len(vec) // 2

    left = vector(vec[:half])
    right = vector(vec[half:])
    return left * val + right * (1 / val)

这里 val 是验证者先前发送的挑战。

理解 L 和 R 交叉项

在折叠时，我们不仅仅是缩小向量。我们还创建了一些“溢出”项，协议称之为 L 和 R：

$L = \langle a_L, b_R \rangle = \langle (a_1 a_2), (b_3 b_4) \rangle$ $R = \langle a_R, b_L \rangle = \langle (a_3 a_4), (b_1 b_2) \rangle$

这些是证明的关键部分。证明者需要将它们发送给验证者。

def get_LR(a, b):
    assert len(a) == len(b)
    assert len(a) % 2 == 0

    half = len(a) // 2

    aL = vector(a[:half])
    aR = vector(a[half:])
    bL = vector(b[:half])
    bR = vector(b[half:])

    L = aL * bR
    R = aR * bL
    return L, R

把它放在一起：缩减步骤

让我们检查一下当我们折叠然后取内积时会发生什么：

$\langle \vec{a'}, \vec{b'} \rangle = \langle (a_1 x + a_3 x^{-1} a_2 x + a_4 x^{-1}), (b_1 x^{-1} + b_3 x b_2 x^{-1} + b_4 x) \rangle = (a_1 x + a_3 x^{-1})(b_1 x^{-1} + b_3 x) + (a_2 x + a_4 x^{-1})(b_2 x^{-1} + b_4 x) = (a_1 b_1 + a_1 b_3 x^2 + a_3 b_1 x^{-2} + a_3 b_3) + (a_2 b_2 + a_2 b_4 x^2 + a_4 b_2 x^{-2} + a_4 b_4) = a_1 b_1 + a_2 b_2 + a_3 b_3 + a_4 b_4 + (a_1 b_3 + a_2 b_4) x^2 + (a_3 b_1 + a_4 b_2) x^{-2} = \langle \vec{a}, \vec{b} \rangle + L x^2 + R x^{-2}$

瞧：交叉项自然地出现了。

因此，在每一轮中，证明者将 (L, R) 发送给验证者，然后双方都进入下一轮。

关键细节：

挑战 x 必须在证明者承诺 L 和 R 之后 采样。否则，证明者可能会找到作弊的方法 😱。

这就是为什么顺序很重要的原因：

1. 证明者计算 L 和 R

2. 验证者发送挑战 x（或者它是通过 Fiat–Shamir 推导出来的）

3. 折叠发生

如果我们颠倒顺序，证明者可以伪造 L 和 R 以使所有内容都核对无误，即使 a 和 b 的内积实际上不是 c。

协议的一整轮

公式足够了，让我们看看一个完整的轮次在 Sage 中是如何工作的：

p = 929
Fp = GF(p)

def fold(vec, val):
        ...

def get_LR(a, b):
    ...

## This needs to be even length
a = vector([Fp.random_element() for _ in range(8)])
b = vector([Fp.random_element() for _ in range(8)])

c = a * b
print("We want to prove that c = a * b")
print("c = ", c)

print("\nRound 1:")
print("inner product round 1 = ", c)
L1, R1 = get_LR(a, b)

x1 = Fp.random_element()
print(f"\nRandom challenge x1: {x1}\n")

a_prime1 = fold(a, x1)
b_prime1 = fold(b, 1 / x1)
print("a_prime1 = ", a_prime1)
print("b_prime1 = ", b_prime1)

c_prime1 = c + (L1 * x1 ^ 2) + (R1 * x1 ^ (-2))
assert c_prime1 == a_prime1 * b_prime1
print("Round 1 successful")
print("Prover sends L1 and R1 to the Verifier\n")

折叠、重复、证明

我们不断折叠，直到 $\vec{a}$ 和 $\vec{b}$ 缩小到长度 1。

例如，假设我们从 8 个条目开始。这意味着 3 轮折叠。到最后，验证者收到了：

$(L_1, R_1), (L_2, R_2), (L_3, R_3), \vec{a'''}, \vec{b'''}$

和挑战：$x_1, x_2, x_3$。

验证者检查：

$c =? \langle \vec{a'''}, \vec{b'''} \rangle - (x_1^2 \cdot L_1 + x_1^{-2} \cdot R_1) - (x_2^2 \cdot L_2 + x_2^{-2} \cdot R_2) - (x_3^2 \cdot L_3 + x_3^{-2} \cdot R_3)$

这之所以有效，是因为每一轮的内积都会“展开”到前一个内积中，一直回到原始的 $\langle \vec{a}, \vec{b} \rangle = c$。

$\langle \vec{a'''}, \vec{b'''} \rangle = \langle \vec{a''}, \vec{b''} \rangle + (x_3^2 \cdot L_3 + x_3^{-2} \cdot R_3)$ $\langle \vec{a''}, \vec{b''} \rangle = \langle \vec{a'}, \vec{b'} \rangle + (x_2^2 \cdot L_2 + x_2^{-2} \cdot R_2)$ $\langle \vec{a'}, \vec{b'} \rangle = \langle \vec{a}, \vec{b} \rangle + (x_1^2 \cdot L_1 + x_1^{-2} \cdot R_1)$ $\langle \vec{a}, \vec{b} \rangle = c$

让我们编写代码

我们现在逐步演练协议，使用小向量，以便你可以清楚地看到折叠和交叉项的发生。

p = 929
Fp = GF(p)

def fold(vec, val):
        ...

def get_LR(a, b):
    ...

## This needs to be even length
a = vector([Fp.random_element() for _ in range(8)])
b = vector([Fp.random_element() for _ in range(8)])

c = a * b
print("We want to prove that c = a * b")
print("c = ", c)

print("\nRound 1:")
...

print("\nRound 2:")
c2 = a_prime1 * b_prime1
print("inner product round 2 = ", c2)
L2, R2 = get_LR(a_prime1, b_prime1)

x2 = Fp.random_element()
print(f"\nRandom challenge x2: {x2}\n")

a_prime2 = fold(a_prime1, x2)
b_prime2 = fold(b_prime1, 1 / x2)
print("a_prime2 = ", a_prime2)
print("b_prime2 = ", b_prime2)

c_prime2 = c2 + x2 ^ 2 * L2 + x2 ^ (-2) * R2
assert c_prime2 == a_prime2 * b_prime2
print("Round 2 successful")
print("Verifier receives L2, R2\n")

print("\nRound 3:")
c3 = a_prime2 * b_prime2
print("inner product round 3 = ", c3)
L3, R3 = get_LR(a_prime2, b_prime2)

x3 = Fp.random_element()
print(f"\nRandom challenge x3: {x3}\n")

a_prime3 = fold(a_prime2, x3)
b_prime3 = fold(b_prime2, 1 / x3)
print("a_prime3 = ", a_prime3)
print("b_prime3 = ", b_prime3)

c_prime3 = c3 + x3 ^ 2 * L3 + x3 ^ (-2) * R3
assert c_prime3 == a_prime3 * b_prime3
print("Round 3 successful", c_prime3)
print("Verifier receives L3, R3\n")

print("a and b now have length 1")
print("We can send a_prime3 and b_prime3 to the verifier")

print("\nVerifier now has: a_prime3, b_prime3, L3, R3, L2, R2, L1, R1\n")

验证者现在可以只检查最终的相等性：

assert c == a_prime3 * b_prime3 \
    - (x1 ^ 2 * L1 + x1 ^ (-2) * R1) \
    - (x2 ^ 2 * L2 + x2 ^ (-2) * R2) \
    - (x3 ^ 2 * L3 + x3 ^ (-2) * R3)

print("Verification successful!")

你可以在这里找到完整的脚本：https://github.com/teddav/bulletproof-ipa/blob/main/ipa-simple.sage

运行它使折叠过程变得切实可行：你看到每一轮如何添加交叉项，挑战如何进入，以及验证者如何将所有内容都与原始声明联系起来。

这就是没有承诺或零知识的内积参数的核心思想。

作弊？

但是......如果我们在这里停止，证明者仍然可以作弊。

一旦挑战被确定，他们就无法伪造折叠步骤，但是他们可以从完全假的向量 $\vec{a'}, \vec{b'}$ 开始，这些向量恰好给出了正确的内积 c。

$\langle \vec{a'}, \vec{b'} \rangle = \langle \vec{a}, \vec{b} \rangle = c$

并且验证者将无法知道哪个pair是正确的，因为没有任何东西将证明与原始向量联系起来。

我写了一个快速的例子：https://github.com/teddav/bulletproof-ipa/blob/main/ipa-cheat.sage

锁定它：承诺！

为了防止作弊，我们需要证明者在协议开始之前将自己绑定到 $\vec{a}$ 和 $\vec{b}$。输入 Pedersen 承诺。

我们设置两个椭圆曲线点的向量：

$\vec{G} = (G_1, ..., G_n)$ $\vec{H} = (H_1, ..., H_n)$

p = 929
Fp = GF(p)
E = EllipticCurve(Fp, [5, 15])
G = E.gens()[0]
Fr = GF(G.order())
assert is_prime(G.order())

Gs = [E.random_point() for _ in range(N)]
Hs = [E.random_point() for _ in range(N)]

在我们的脚本中，我们使用随机点来简化操作，但显然 $\vec{G}, \vec{H}$ 是固定的公共生成器，每个人都知道。

然后我们将承诺定义为：

$C_a = \langle \vec{a}, \vec{G} \rangle$ $C_b = \langle \vec{b}, \vec{H} \rangle$

接下来，我们还使用另一个随机曲线点 Q 承诺声明的内积（选择它，以便没有人知道它与其他基的离散对数关系）：

$C_{ab} = \langle \vec{a}, \vec{b} \rangle \cdot Q$

最后，我们将所有内容粘合到一个“主”承诺 P 中：

$P = C_a + Cb + C{ab}$

这个 P 是我们将要折叠的对象，就像我们之前对普通向量所做的那样。

神奇之处在于 P 的结构确保了验证者仍然可以仅通过对数通信来检查所有内容，但是现在证明者无法换入假向量，因为他们的承诺从一开始就将他们与 $\vec{a}, \vec{b}$ 捆绑在一起。

完整协议的实际应用

你猜对了：该协议与以前完全相同，不同之处在于证明者需要做更多的工作，因为我们现在处理三个不同的内积及其承诺。

我不会详细介绍每一个细节，但是让我们简要地看一下一个轮次是如何进行的。

交叉项

交叉项现在涉及向量 $\vec{G}$ 和 $\vec{H}$。

和以前一样，我们将 $x_L$ 称为向量 $\vec{x}$ 的左半部分，将 $x_R$ 称为右半部分。

$L = \langle a_L, G_R \rangle + \langle b_R, H_L \rangle + \langle a_L, b_R \rangle \cdot Q$ $R = \langle a_R, G_L \rangle + \langle b_L, H_R \rangle + \langle a_R, b_L \rangle \cdot Q$

def get_LR(a, b, Gs, Hs):
    assert len(a) == len(b)
    assert len(a) % 2 == 0
    half = len(a) // 2

    aL = a[:half]
    aR = a[half:]

    bL = b[:half]
    bR = b[half:]

    GL = Gs[:half]
    GR = Gs[half:]

    HL = Hs[:half]
    HR = Hs[half:]

    L = inner_product(aL, GR) + inner_product(bR, HL) + \
        inner_product(aL, bR) * Q

    R = inner_product(aR, GL) + inner_product(bL, HR) + \
        inner_product(aR, bL) * Q

    return L, R

折叠

以前我们只折叠了 $\vec{a}$ 和 $\vec{b}$。现在我们需要折叠：$\vec{a}, \vec{b}, \vec{G}, \vec{H}$。

这给出了：

$\vec{a'} = fold(\vec{a})$ $\vec{b'} = fold(\vec{b})$ $\vec{G'} = fold(\vec{G})$ $\vec{H'} = fold(\vec{H})$ $P' = \langle \vec{a'}, \vec{G'} \rangle + \langle \vec{b'}, \vec{H'} \rangle + \langle \vec{a'}, \vec{b'} \rangle \cdot Q$

def fold(vec, val):
    assert len(vec) % 2 == 0
    half = len(vec) // 2

    left = vec[:half]
    right = vec[half:]
    return [left[i] * val + right[i] * (1 / val) for i in range(half)]

我们现在可以检查：

$P' = P + x^2 \cdot L + x^{-2} \cdot R$

这很容易！

现在我们有了一个验证内积的协议，同时将证明者绑定到向量。但是我们可以使验证者的工作更加便宜。

使用 SageMath 自己运行它

让我们看一下一个带有承诺的轮次：

...

print("We define Q as a random point on the curve")
Q = E.random_point()

def inner_product(a, b):
        ...

def fold(vec, val):
        ...

def get_LR(a, b, Gs, Hs):
        ...

## Length of the vectors (this needs to be even length)
N = 8

a = [Fr.random_element() for _ in range(N)]
b = [Fr.random_element() for _ in range(N)]

c = inner_product(a, b)
print("We want to prove that c = a * b")
print("c = ", c)

P = inner_product(a, Gs) + inner_product(b, Hs) + c * Q
print("P = ", P)

print("\nRound 1:")

L1, R1 = get_LR(a, b, Gs, Hs)

x1 = Fr.random_element()
print(f"\nRandom challenge x1: {x1}\n")

a_prime1 = fold(a, x1)
b_prime1 = fold(b, 1 / x1)
G_prime1 = fold(Gs, 1 / x1)
H_prime1 = fold(Hs, x1)

P_prime1 = inner_product(a_prime1, G_prime1) + inner_product(b_prime1,
                                                             H_prime1) + inner_product(a_prime1, b_prime1) * Q

assert P_prime1 == P + x1 ^ 2 * L1 + x1 ^ (-2) * R1
print("Round 1 successful")
print("Verifier receives L1, R1\n")

print("\nRound 2:")

...

print("Round 2 successful")
print("Verifier receives L2, R2\n")

print("\nRound 3:")

...

print("Round 3 successful")
print("Verifier receives a_prime3, b_prime3, L3, R3\n")

在这里找到完整的脚本：https://github.com/teddav/bulletproof-ipa/blob/main/ipa-with-commitment.sage

验证者的最终检查

对于验证，验证者通过对 $\vec{G}$ 和 $\vec{H}$ 重复所有 fold 操作，使用挑战 $x_i$ 自己重新计算折叠的基。

print("\nVerification:")
print("Verifier now has: a_prime3, b_prime3, (L1, R1), (L2, R2), (L3, R3)\n")

print("He recomputes P_prime3:")
print("First needs to recompute G_prime3 and H_prime3, from the initial Gs and Hs")
verifier_G_prime1 = fold(Gs, 1 / x1)
verifier_G_prime2 = fold(verifier_G_prime1, 1 / x2)
verifier_G_prime3 = fold(verifier_G_prime2, 1 / x3)
assert verifier_G_prime3 == G_prime3
verifier_H_prime1 = fold(Hs, x1)
verifier_H_prime2 = fold(verifier_H_prime1, x2)
verifier_H_prime3 = fold(verifier_H_prime2, x3)
assert verifier_H_prime3 == H_prime3
print("verifier_G_prime3 = ", verifier_G_prime3)
print("verifier_H_prime3 = ", verifier_H_prime3)

然后他重新计算最终的 P

verifier_P_prime3 = inner_product(a_prime3, verifier_G_prime3) + inner_product(
    b_prime3, verifier_H_prime3) + inner_product(a_prime3, b_prime3) * Q
print("verifier_P_prime3 = ", verifier_P_prime3)

并执行最终检查：

final_check = verifier_P_prime3 \
    - (x1 ^ 2 * L1 + x1 ^ (-2) * R1) \
    - (x2 ^ 2 * L2 + x2 ^ (-2) * R2) \
    - (x3 ^ 2 * L3 + x3 ^ (-2) * R3)
assert final_check == P

print("Verification successful!")

优化验证

如前所述，验证者需要通过重复所有 fold 操作来重新计算折叠的基，这需要大量的昂贵的椭圆曲线操作…

但是有一个技巧！每个最终的折叠基（$\vec{G'}$ 和 $\vec{H'}$ 的每个坐标）都是原始基的线性组合，其系数仅取决于挑战 $x_1, x_2, ..., x_k$。

换句话说：在 k 轮之后，每个原始基 $G_i$ 都恰好贡献于最终向量 $\vec{G'}$ 的一个坐标。我们通过一个系数 $s_i$ 缩放 $G_i$，该系数是挑战的幂的乘积（$x_r$ 或 $x_r^{-1}$）。

$\vec{H}$ 基也是如此。

因此，验证者可以一次性完成此操作，而不是重复折叠点：

1. 计算每个原始 $G_i$ 的权重 $s_i$（以及 $H_i$ 的 $s_i^{-1}$）

2. 使用单个多标量乘法计算最终的折叠基：

$G' = \langle \vec{s}, \vec{G} \rangle = \sum_{i=0}^{N-1} s_i Gi$ $H' = \langle \vec{s^{-1}}, \vec{H} \rangle = \sum{i=0}^{N-1} s_i^{-1} H_i$

计算验证权重

• 对于原始向量中的每个元素，取其索引 i
• 用 k 位写出其二进制表示形式，其中 k 是折叠轮次的次数（$k = \log_2(N)$）
• 循环遍历每个位：
• 如果该轮的位是 0（表示 $G_i$ 在该轮的左半部分），我们将乘以 $x_r^{-1}$
• 如果该位是 1，我们使用 $x_r$

对于 H，则相反。

$si = \prod{j=0}^{k-1} \begin{cases} x_j & \text{if } bit_j(i) = 1 \ x_j^{-1} & \text{if } bit_j(i) = 0 \end{cases}$

这与折叠期间发生的情况相符：

• 对于 $\vec{G}$，左侧部分乘以 $\frac{1}{x_r}$，右侧部分乘以 $x_r$
• 对于 $\vec{H}$，则相反

如果更容易，你可以将其视为一棵树：

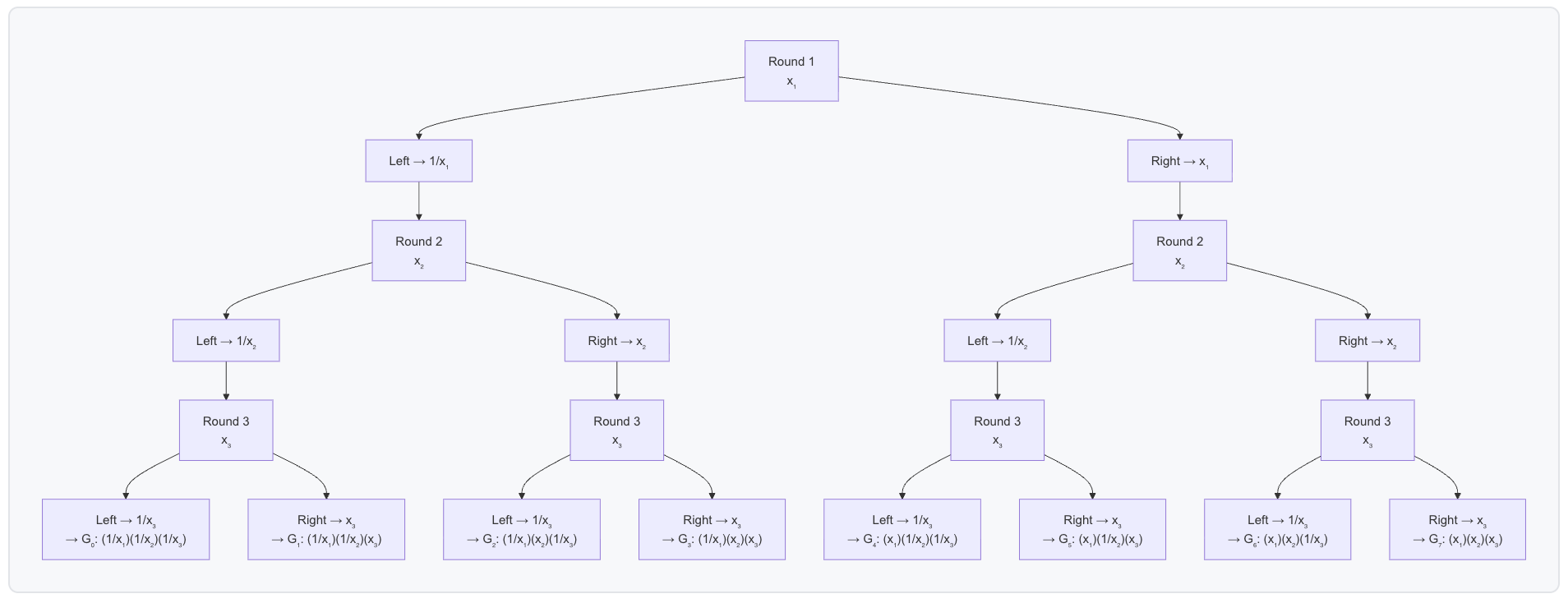
这是一个小的 Sage 助手，可以一次性计算所有最终权重，然后计算最终的折叠基：

xs = [x1, x2, x3]

s_G = [Fr(1) for _ in range(N)]
s_H = [Fr(1) for _ in range(N)]

for i in range(N):
    i_bits = bin(i)[2:].zfill(int(math.log(N, 2)))
    for k in range(int(math.log(N, 2))):
        bit_j = int(i_bits[k])
        if bit_j == 1:
            s_G[i] *= xs[k]
            s_H[i] *= 1 / xs[k]
        else:
            s_G[i] *= 1 / xs[k]
            s_H[i] *= xs[k]

print("s_G = ", s_G)
print("s_H = ", s_H)

G_final = inner_product(s_G, Gs)
H_final = inner_product(s_H, Hs)
assert G_final == G_prime3[0]
assert H_final == H_prime3[0]

这样，验证者跳过了 $\log N$ 轮折叠，并将其替换为单个多标量乘法，大多数库都可以非常有效地评估它。在验证成本方面取得了巨大的胜利。

就是这样！ 🥳 你已经从头开始构建了一个完整的内积参数！

我们从普通向量开始，学习了折叠如何一轮又一轮地减少它们，然后添加承诺以使所有内容都合理且可验证。最后，我们通过一些巧妙的优化使验证者的生活更加轻松。

请继续关注下一部分，我们将研究 Bulletproofs 的一个实际用例：范围证明 🤯

zkSecurity 提供审计、研究和开发服务，适用于包括零知识证明、MPC、FHE 和共识协议在内的加密系统。

了解更多 →

• 原文链接： blog.zksecurity.xyz/post...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～