基于哈希函数的签名（二）：少量次数签名

作者：David Wong

来源： https://cryptologie.net/posts/hash-based-signatures-part-ii-few-times-signatures/

前篇见此处

如果你错过了本系列 上一篇 关于一次性签名的文章（ 中文译本），请先看去看它。本文讲的是一种更有用一点的构造，允许使用同一对较小体积的 公钥/私钥 生成多于一个签名。本系列文章的终极目标是解释基于哈希函数的签名方案是如何构造的 —— 它们的应用可不仅仅是一次性签名（OTS）和少量次数签名（FTS）而已。

为了完整起见，下列段落引自一篇关于其它已被研究的应用：

一次性签名已经应用到了各种签名方案的构造中：常规签名方案 [Mer87, Mer89] ，前向安全的签名方案 [AR00] ，在线/离线 的签名方案 [EGM96] ，以及 流式/多播 身份认证 [Roh99] ，等等 …… 还有 [Per01] 的 Biba 广播身份认证方案

但废话少说！今天我们的话题是 HORS！

HORS

HORS 是 “Biba”（“Bins and Balls”） 的升级，由 Reyzin 父子出版于 2022 年，论文为《 比 Biba 更好：更短的一次性签名、更快的签名和验证》。

第一种构造，基于单向函数，从跟 OTS 非常相似的地方开始：生成一组整数，作为你的私钥；然后哈希每一个整数，这样就获得了公钥。

但到了要签名的时候，你将需要一种 选择函数 $S$ ，它根据你要签名的消息 $m$ 会给你一组索引号。现在我们把它抽象一下。

在下面的案例中，我选择了参数 $t = 5$ 以及 $k = 2$ 。它们意味着，我可以签名其（在表示为一个整数时）十进制数值小于 $\binom{t}{k} = 10$ 的消息。它也表明，我的私钥（以及相应的公钥）的长度将是 5 ，而我的签名的长度将是 2 （因为选择函数 S 将输出 2 个索引号）。

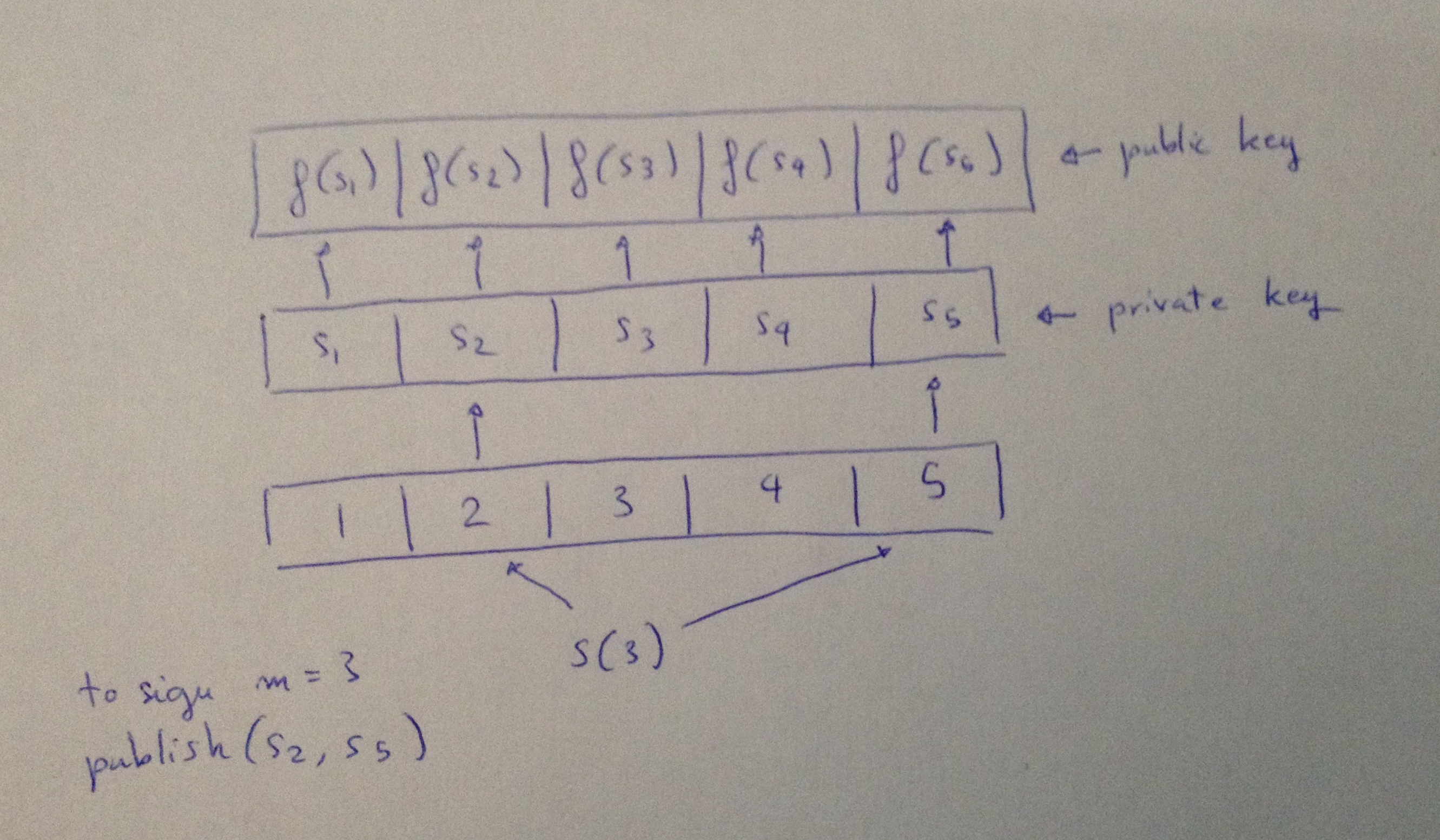
使用一个好的挑选函数 S（一种双射函数（bijective function）），使用来自同一个私钥的相同元素来签名两条不同的消息将是 不可能的。但是，依然，在同一个私钥签名两次之后，伪造一个签名就会变得非常容易。

（译者注：“双射” 意味着两个集合内的元素拥有一一对应的关系，双射函数表达的就是这样的关系，这也意味着它是可以逆转的。）

第二种构造则是我们说的 HORS 签名方案。它基于 “子集抗性（subset-resilitient）” 函数，而不是单向函数。挑选函数 $S$ 也被替代成另一种函数 $H$ ，它让不可能找出两条消息 $m_1$ 和 $m_2$ 使得 $H(m_2) \subseteq H(m_1)$ 。

此外，如果我们希望这种方案成为一种少量次数签名方案，如果签名人提供了签名 $r$ ，那么应该无法找出另一条消息 $m’$ 能让 $H(m’) \subseteq H(m_1) \cup \dots \cup H(m_r)$ 。这正是 “子集抗性” 的定义。如果任何攻击者，在多项式时间内，都无法（哪怕是以小概率）找出一组 $(r + 1)$ 条消息使上述方程成立，我们就说，我们的选择函数 $H$ 是 “r-子集抗性的”。论文中有具体的定义（但大体上就是我说的这样）。

所以，回到相同的例子：

但现在，选择函数不再是一种双射函数，所以它是难以逆转的。即使知道以往对一组消息的签名，也难以知道什么消息会使用这样的索引号。

在理论上，这是通过使用 一种 随机断言机（random oracle）来实现的；而在实践中，就是使用一种哈希函数。这也是为什么这种方案被称为 “ HORS” —— 它是 “以哈希函数获得随机子集（ Hash to Obtain Random Subset）”的缩写。

如果你真的好奇，以下是我们的新的选择函数：

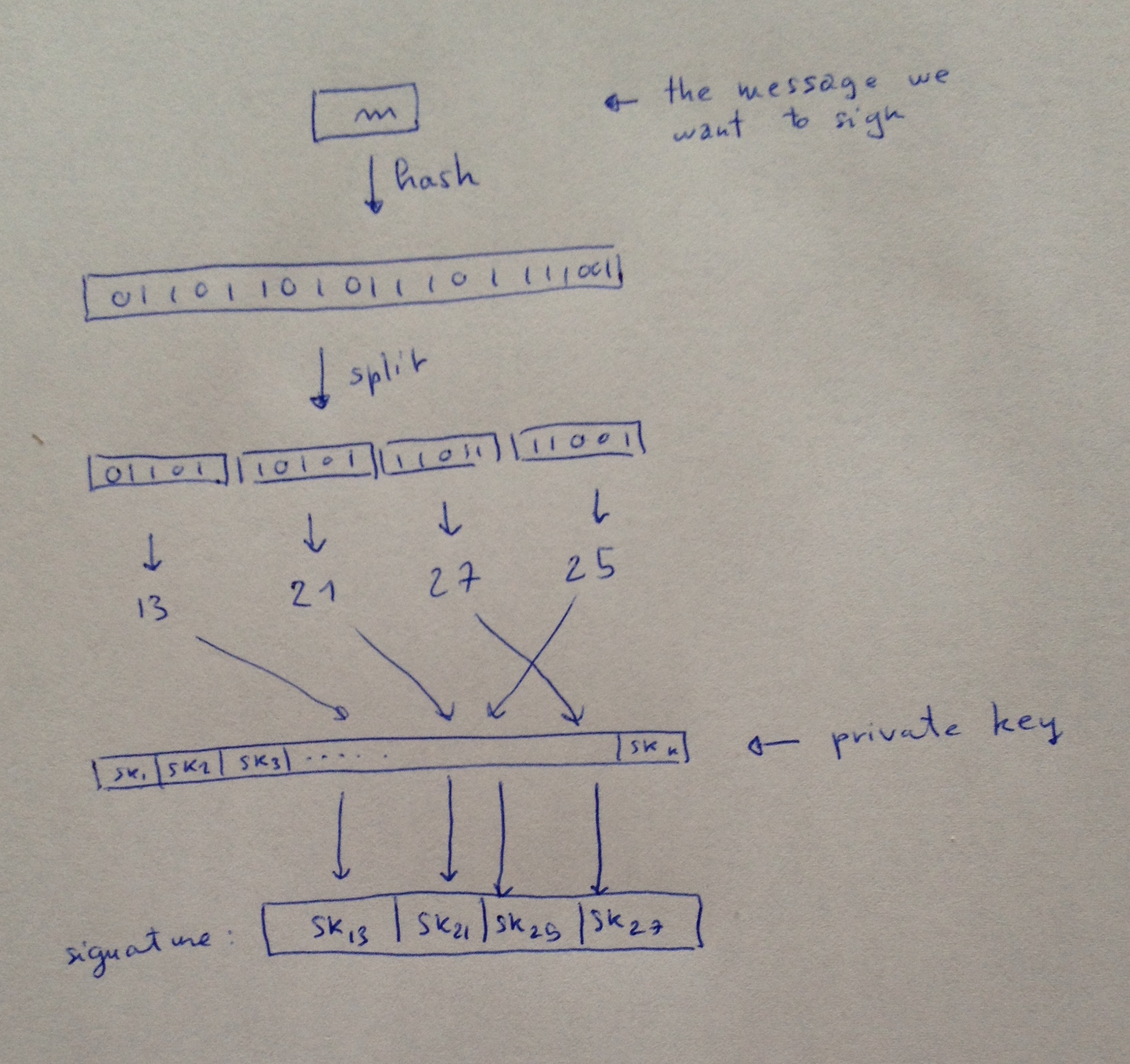
在签名消息 $m$ 时：

1. $h = Hash(m)$
2. 将 $h$ 分割为 $(h_1, \dots, h_k)$
3. 将每一个 $h_j$ 解释为一个整数 $i_j$
4. 签名就是 $(sk_{i1}, \dots, sk(i_k))$

既然人们都喜欢我的画，我就勉为其难再画一辐：

本系列第三篇在这里

• 本文转载自： btcstudy.org/2026/01/06/... , 如有侵权请联系管理员删除。