ZK 编年史：电路（第二部分）

如果你还记得，在之前的几篇文章中，我们介绍了电路可满足性问题（包括 CSAT 和 #SAT 两种版本），这直接引导我们进入了传统电路的一种强大扩展形式——算术电路。

虽然这些问题在概念上很有趣，但它们可能仍然让人觉得有点别扭。而且当时，我们声称，对于我们的目的来说，一个更直观的替代方案是某种程度上证明电路求值的正确性——你知道，证明在特定输入集上对电路求值会产生所声称的结果。

我们今天的目标是提出一种机制来实现这一点。

我必须警告你：这将比之前的文章稍微复杂一些。然而，它将引导我们走向感觉像是我们第一个真正通用的证明系统。

众多证明系统中的第一个！

不过不要太担心！和往常一样，我们将一步一步地进行，把重要的部分分解开来。

有很多内容要讲，所以拿好你的咖啡，坐稳了——这将是一篇很长的文章！

证明求值

好了！鉴于我们已经了解了算术电路，我们可以直接进入手头的问题。

给定某个算术电路 φ(X)，我们的目标是证明对于某个输入 x，电路的输出具有某个值 y：

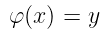
$\varphi (x) = y$

我想让我们花点时间来分析如何处理这个问题。

我们目前没有任何明确的提示。对于 #SAT，超立方体求和使得与和校验的联系显而易见，但我们在这里没有同样的运气。我们需要另一个攻击角度。

也许我们应该回顾一下我们到目前为止的知识，这将给我们一个前进方向。让我们看看：我们知道算术电路由加法和乘法门组成。并且每当你向电路输入一些输入时，它会通过导线向前流动并进入门（记住，它是一个有向无环图），这些门执行简单的运算。

这里有一个简单的问题：如果一个门被错误计算会发生什么？

到目前为止，我们几乎都在假设“快乐路径”，但如果情况并非如此呢？任何一个门的单个不正确计算都会导致通过电路的连锁反应，使整个计算无效。

反之，我们也可以说，为了使整个电路的结果正确，每个门都必须被正确计算。

是的，由于模运算，结果意外保持正确的可能性很小。但在一个大小合适的域中，这种概率可以忽略不计，所以我们可以安全地忽略它！

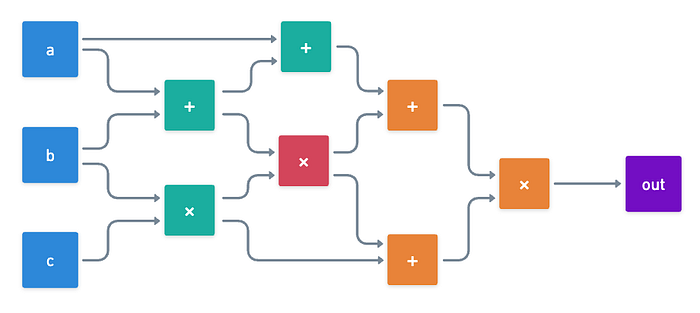
红色门被错误计算，因此依赖于其结果的门也是错误的

这给了我们一个极其强大的洞察力：我们可以将检查电路求值的问题分解为检查单个门的正确求值。

这主要就是电路作为一种计算模型的强大之处的来源！门有点像是可验证计算的 乐高积木：你可以检查它们的正确性，并且可以将它们链接在一起来形成更丰富的结构！

除非你不能踩到电路

很好！这似乎是一个很有希望的起点。我们现在需要的是一种利用这种新发现的知识的方法。

相关信息

为了构建一个证明系统，验证者应该能够探测这些门来检查它们是否被正确计算。这通常通过一种编码策略来完成：一个门上的计算以某种验证者可以自己使用的形式表达。

那么我们该怎么做呢？

嗯，验证者至少需要三件事才能成功检查一个门计算是否有效：

• 输入
• 输出
• 门的类型（加法或乘法）

如果一个验证者可以掌握这些东西，他们可以简单地计算预期的输出，并与所提供的结果进行比较！

至少理论上是这样——但我们如何编码这些信息呢？

编码

答案可能并不令人惊讶：多项式！

永远是多项式！

没有单一的方法可以做到这一点。不同的证明系统使用不同的技术——这也是现代证明系统之间主要区别的来源之一。

我想让我们通过一个例子来热热身。让我们看看用一个小电路我们可以做什么：

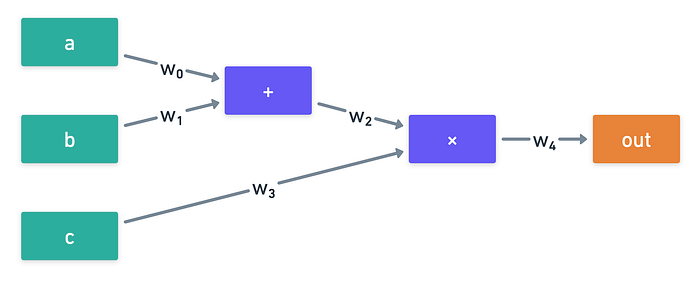
(a + b).c 的简单电路

这里有一些想法。首先，我们想要编码导线值。我们总共有 5 根导线，所以我们可以创建一个多项式 W(X)，使得：

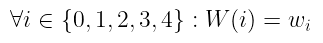
$\forall i \in {0,1,2,3,4} : W(i) = w_i$

请注意，这些是 求值 ——我们将在后面详细介绍如何获得实际的多项式 W(X)。

Then, we’d need to encode gate information. To do this, we can use indicator polynomials for each gate: one for addition gates, and one for multiplication gates.

Then, we’d need to encode gate information. To do this, we can use indicator polynomials for each gate: one for addition gates, and one for multiplication gates.

然后，我们需要编码门信息。为此，我们可以对每个门使用指示多项式：一个用于加法门，一个用于乘法门。

以类似于拉格朗日基的方式，我们可以选择一个门 g，并构造一个多项式 $A^{g}(X,Y,Z)$，它只在以下情况下返回 1：

• X、Y 和 Z 的值对应于门的正确导线，其中 X 是左输入，Y 是右输入，Z 是输出。
• 门 g 是一个加法门。

对于乘法门，以及多项式 Mᵍ(X,Y,Z) 也可以做同样的事情.

有了这个，我们可以用这个表达式来表示“门 g 被正确求值”的说法：

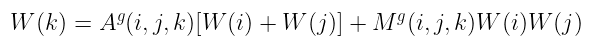
$W(k) = A^g(i, j, k)[W(i) + W(j)] + M^g(i, j, k)W(i)W(j)$

Aᵍ 和 Mᵍ 的作用是在它们不对应于正确的门时，以某种方式停用检查！当然，我们应该确保 Aᵍ 和 Mᵍ 不同时等于 1！

好的，暂停一下。这可能有很多信息！

花点时间让所有这些知识沉淀下来。当我们进入这个系列的后续内容时，这些类型的编码策略将非常重要，所以最好现在就熟悉它们！

认真地，慢慢来。如果你跳过，我会知道的。

我在看着你

很好？好吧，我们继续前进！

门编码，完成。

不幸的是……这里有一个非常明显的问题：为了检查电路求值的正确性，验证者需要检查每一个门。对于大型电路（其中大小 S 很大），这将意味着 O(S) 的验证时间。

这非常糟糕，因为它不比简单地运行电路更好——而可验证计算的整个要点是允许验证者运行得更快！

我们在我们的计划中遇到了一个巨大的障碍……我们能做得更好吗？

结构化电路

有时我们可以！

秘密在于意识到并非所有电路都是相同的。事实上，所有电路都有不同的总体结构。在某些情况下，我们可以利用它来获得更好的性能。

特别是，我们对可以识别出清晰层的电路感兴趣：彼此没有直接连接（它们是独立的）的门组，而是仅依赖于前一层。

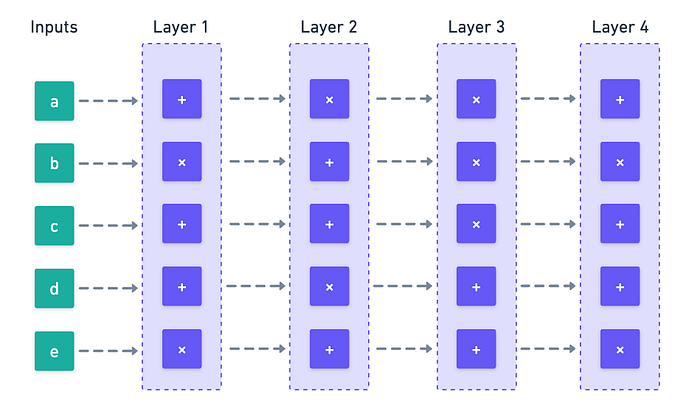
我们将层的数量称为电路的 深度（ d），每层中的导线数量表示该层的 宽度（ w _）。对于宽度相对均匀的电路，电路的总大小约为 S ≈ d·w。

现在……如果我们能够证明整个层在一次操作中被正确计算，会发生什么？

如果我们能够实现这一点，我们可能会节省大量时间——特别是对于浅层电路，其深度远小于其宽度。

一些协议确实利用了这种结构。我们的下一个主题就是这种情况：GKR 协议。

GKR 协议

GKR 代表该技术创建者的姓名首字母：Goldwasser、Kalai 和 Rothblum。密码学中的几种技术都采用了这种命名方式。

现在，这将结合我们到目前为止所学到的一切：结构化电路、多项式编码、多线性扩展 和 和校验。

根据个人经验，我的建议是不要着急。如果需要，请回到之前的概念。这篇文章不会消失——这一点我可以向你保证！

电路布局

GKR 协议假定电路具有非常特定的结构。它不仅是分层的，而且每一层都有预定数量的门。

让我们用索引 i 标记每一层。从索引为 0 的输出层开始，并向后计数到输入，每一层总共有 $Sᵢ =$ $2^{kᵢ}$ 个门。

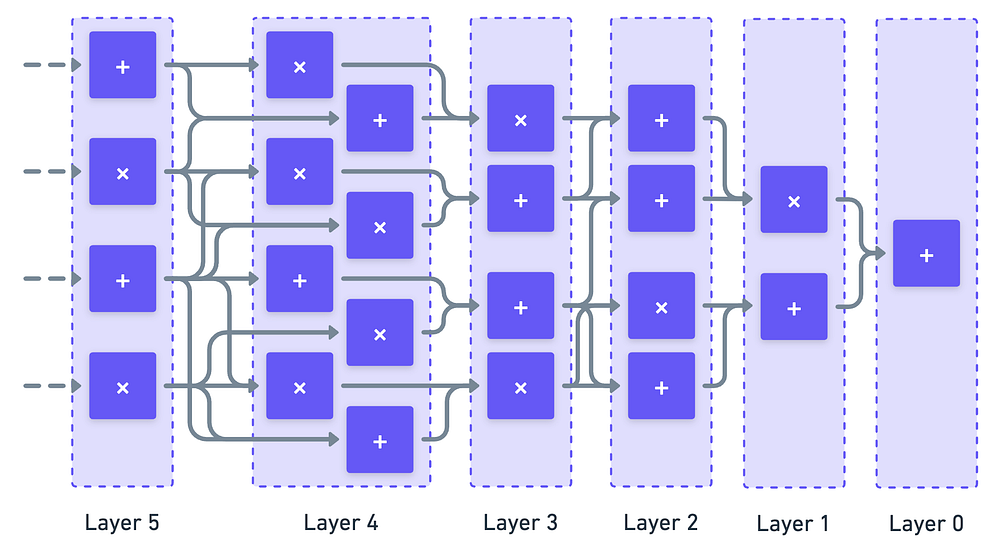
请注意，kᵢ 是与每一层相关联的值！

关于这种选择并非无意。但我们为什么要强制层具有如此奇怪的特定数量的门？

原因是我们过去已经利用过的一个：索引！

Essentially, we can label each gate (or equivalently, each wire) of any given layer i using our trusty boolean hypercube! We encode the values for each gate as evaluations of some function $Wᵢ(X)$:

从本质上讲，我们可以使用我们值得信赖的布尔超立方体来标记任何给定层 i 的每个门（或等效地，每根导线）！我们将每个门的值编码为某个函数 $Wᵢ(X)$ 的 求值：

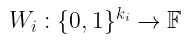
$W_i: {0,1}^{k_i} \rightarrow \mathbb{F}$

其中 Wᵢ(b) 返回 i 层导线 b 上的值（b 是索引导线的 kᵢ 位二进制字符串）。

你知道布尔超立方体意味着什么：一个 和校验 就要来了！

连接层

当然，我们仍然缺少的部分是我们之前谈到的门操作编码。为了获得这个，我们需要再做一件事：指定门是如何连接的。

这就是所谓的连线谓词。它是今天难题中唯一缺失的部分，一旦我们有了这个，我们最终就能将所有东西连接起来。

从字面上看！

为此，让我们定义多项式 $Aᵢ$ 和 $Mᵢ$，它们描述了这个连线谓词：

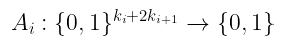
$A_i: {0,1}^{ki + 2k{i+1}} \rightarrow {0,1}$

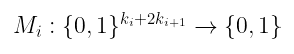
$M_i: {0,1}^{ki + 2k{i+1}} \rightarrow {0,1}$

正如之前所说，这些将采用三个门标签 a、b 和 z——前两个来自输入层，最后一个来自输出层——，并且仅当以下情况时返回 1：

• 组合中的门在电路中是真正连接的，这意味着门 z 具有输入 a 和 b。
• 最右边的门（z）是正确的类型（加法或乘法）。

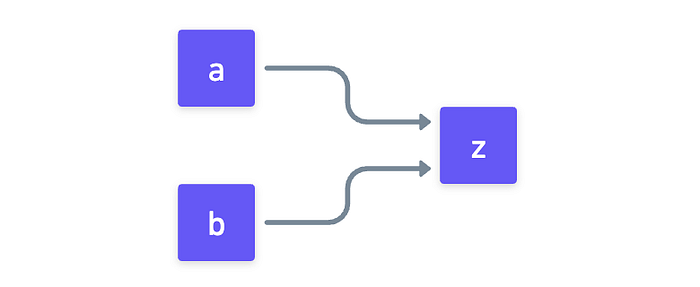
类似地，对于乘法门，Mᵢ(a,b,z) = 1。

而 Wᵢ 编码了第 i 层中导线的值，Aᵢ, Mᵢ 描述了哪些门连接到哪些门，以及它们的类型。它们共同构成了电路的完整描述，或完整编码！

正如前面暗示的那样，剩下的就是以某种方式将其转换为和校验。

构建和校验

如果你还记得，和校验协议有一个非常好的递归结构：原始问题被简化为相同问题的更小版本，最终得到一些几乎可以忽略不计的校验。

那么，我们尝试使用类似的方法怎么样？

这个想法很简单：从输出层开始，具有一些声明的输出值。在那里，我们将尝试将关于输出的声明转换为关于倒数第二层的值的声明。重复执行，经过 d 步后，我们得到了关于输入的声明，验证者应该知道这些输入！

很简单，对吧？

希望你比 Bart 做得更好！

坚强点，伙计们！

为了执行这个简化步骤，我们需要检查关于每一层的 某些东西。这就是我们的编码变得相关的地方，这都要感谢这个小技巧：

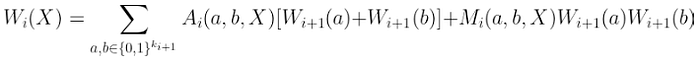
$Wi(X) = \sum{a,b \in {0,1}^{k_{i+1}}} Ai(a,b,X)[W{i+1}(a) + W_{i+1}(b)] + Mi(a,b,X)W{i+1}(a)W_{i+1}(b)$

在你的头脑爆炸之前，让我们试着解释一下这个表达式在做什么：

• 我们正在对 i + 1 层的 所有可能的门索引 进行求和，这些索引是 i 层（此步骤中的输出层）的可能输入
• 然后，我们问：这是一个加法门还是一个乘法门？记住，Aᵢ 和 Mᵢ 返回 0 或 1，并且它们仅当在层上存在具有输入 a 和 b 以及输出 X 的门，并且 当门是指定的类型时才会激活。
• 最后，Aᵢ 和 Mᵢ 乘以期望的运算。

这里的关键点是，尽管对布尔超立方体求和，但只有一个可能的组合会激活 Aᵢ 或 Mᵢ ——因此整个总和简化为仅一项。

例如：如果第 i 层上的导线 5 通过加法门从第 i + 1 层上的导线 2 和 3 获取输入，那么我们有：

• Aᵢ(2,3,5) = 1
• Aᵢ(其他任何值, 5) = 0
• 整个总和简化为 $W{i+1}(2) + W{i+1}(3)$！

现在，与和校验的相似之处更加明显了！

总和内那个疯狂的多项式？让我们直接称之为 $gᵢ(X,Y,Z):$

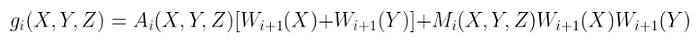
$g_i(X,Y,Z) = Ai(X,Y,Z)[W{i+1}(X) + W_{i+1}(Y)] + Mi(X,Y,Z)W{i+1}(X)W_{i+1}(Y)$

有了它，我们可以将 z 固定为一个特定的值，并应用和校验来验证：

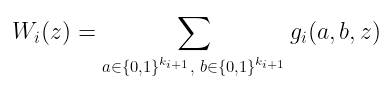
$Wi(z) = \sum{a \in {0,1}^{k{i+1}}, \ b \in {0,1}^{k{i+1}}} g_i(a,b,z)$

请注意，我们正在固定 z，以便连线谓词有意义！

正如你所看到的，在每一层，我们需要来自下一层的值来构建我们正在使用的这个多项式。除非验证者正在查看输入层，否则他们不知道这些值！相反，证明者将提供它们——因此这个和校验将问题简化为关于下一层的声明！

因此，我们只需要应用 d 次（电路的深度），我们就差不多完成了。

剩余的挑战

好的，太棒了！这进展得很好。但是为了继续前进，我们需要解决两个仍然存在的问题，这些问题在我们仔细查看需要在任何单层中执行的和校验时变得清晰。

因此，让我们简要回顾一下和校验协议的进行方式。

1. 首先，证明者将 声明的结果 C₁ 和一个从原始 g(X) 构造的 单变量多项式 P₁(X₁) 发送给验证者。
2. 验证者执行一个简单的检查，然后选择一个随机挑战 r₁，并在该挑战处计算 P₁(r₁)。他们还将此值发送给证明者。
3. 然后，证明者继续证明 C₂ = P₁(r₁) 是新的声明结果——他们通过回到 (1.) 来做到这一点！

重复该过程，直到原始 g(X) 的所有变量都被用完，并且验证者通过执行单个预言机查询来关闭该过程。当然，在我们的例子中，g(X) 是每一层的 gᵢ(X,Y)。

如需完整说明，你可以返回到这篇文章！

现在，这个机制有两个问题：

• 我们需要能够在从一个大的有限域中随机选择的点上计算 gᵢ(X,Y)……但根据定义，这个多项式是在一个布尔超立方体上定义的！
• 只要验证者知道两个特殊值，最终的预言机查询实际上可以由验证者计算：在前一层中随机选择的点上对 W 的求值。但是这些值对验证者来说是未知的！

如果我们设法解决这些问题，那么我们将拥有一个功能齐全的证明系统。让我们一次解决一个问题。

变为多线性

我们开始吧！

因此，我们需要在编码连线谓词的表达式上应用和校验协议：

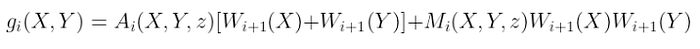
$g_i(X,Y) = Ai(X,Y,z)[W{i+1}(X) + W_{i+1}(Y)] + Mi(X,Y,z)W{i+1}(X)W_{i+1}(Y)$

在和校验期间，我们需要能够为输入的每个分量选择从有限域 𝔽 中选择的随机值。这意味着我们需要扩展这些多项式的域！

虽然有很多方法可以做到这一点，但有一种非常简单且高效的方法可以做到这一点：多线性扩展（MLE）。如果我们对每个涉及的多项式进行 MLE，我们得到一个适合我们需要的表达式：

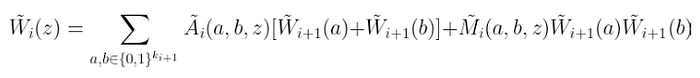
$\tilde{W}i(z) = \sum{a,b \in {0,1}^{k_{i+1}}} \tilde{A}i(a,b,z)[\tilde{W}{i+1}(a) + \tilde{W}_{i+1}(b)] + \tilde{M}i(a,b,z)\tilde{W}{i+1}(a)\tilde{W}_{i+1}(b)$

顺便说一句，我们用波浪号 (~) 符号表示多线性扩展。

对于上面的等式，如果你愿意，可以随意检查它是否成立！

有了这个，我们就能够在每一层上执行和校验！

减少求值

最后，请记住，每个和校验（对于每一层）结束时的预言机查询需要在一些随机选择的输入上对前一层进行两次求值：

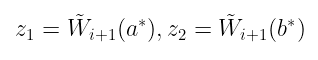
$z1 = \tilde{W}{i+1}(a^), z2 = \tilde{W}{i+1}(b^)$

Now, if we had to perform two checks every time, the number of times we’d need to run the full sum-check would grow exponentially, making our strategy unusable. Therefore, the final touch in our mechanism is to try and combine those two checks into a single one!

现在，如果我们每次都必须执行两个检查，那么我们需要运行完整和校验的次数将呈指数级增长，使我们的策略无法使用。因此，我们机制的最后一点是尝试将这两个检查组合成一个！

这将是其他上下文中一个有用的工具，将来我会链接回本节。别担心！

我们可以为此使用一个非常聪明的技巧。定义：

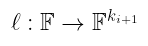
$\ell: \mathbb{F} \rightarrow \mathbb{F}^{k_{i+1}}$

这仅仅是一条线。我们已经知道一条线由两个点定义。我们可以将它们设置为 ℓ(0) = a* 和 ℓ(1) = b*。

现在这条线编码了两个值。

有了这个，我们将定义一个小子协议。这是它的工作方式：

• 证明者发送一个次数至多为 $kᵢ$ ₊₁ 的单变量多项式，声明等于：

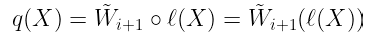
$q(X) = \tilde{W}{i+1} \circ \ell(X) = \tilde{W}{i+1}(\ell(X))$

• 验证者然后检查 z₁ = q(0) 和 z₂ = q(1)。这验证了至少这个声明的多项式 q(X) 编码了所需的值。
• 最后，验证者选择一些随机点 r*，并使用它计算：

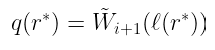
$q(r^) = \tilde{W}_{i+1}(\ell (r^))$

所以，这里发生了什么？证明者本质上是为验证者提供了一种“安全地”计算下一层和校验的 $Wᵢ$ ₊₁ 的方法：

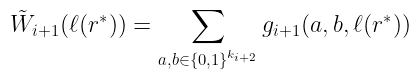
$\tilde{W}{i+1}(\ell(r^*)) = \sum{a,b \in {0,1}^{k{i+2}}} g{i+1}(a,b,\ell(r^*))$

请注意，此检查不对应于在下一层上选择一个随机层。相反，我们使用一些随机值 ℓ(r*)，它很可能不会位于有效的门索引处，而是位于其他一些点上！

关键的想法是证明者事先不知道 r*。因此，如果 q(X) 实际上是不正确的（我们称之为 q’），我们根据 Schwartz-Zippel 引理知道，很可能：

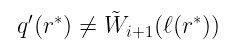
$q’(r^) \neq \tilde{W}_{i+1}(\ell (r^))$

这将使证明者的生活非常困难，因为他们必须使用错误的声明总和继续下一轮和校验，为此他们不能使用实际的导线多项式。

考虑到这两个因素，该协议已完全定义！

流程如下：

• 证明者将电路层编码为多项式，并计算它们的多线性扩展。
• 从最后一层开始，证明者和验证者使用输出值作为初始声明进行一轮和校验。
• 证明者通过 q(X) 将两个所需的 W 求值减少为单个求值，并将 q(X) 发送给验证者。然后，验证者计算下一轮和校验的声明。
• 重复执行，直到到达输入层，此时验证者可以自行完成验证（不需要预言机访问！）。

分析

不过，和往常一样，我们需要评估该协议的一些关键方面，以确定它是否有意义：即完整性、可靠性和成本分析。

我知道伙计们此时可能已经很累了。这本身已经是一颗知识炸弹。

tl;dr：GKR 是可靠的，具有可忽略的误差，验证者大约在 O(d·log S) 中运行，但证明者在 O(S³) 处运行成本很高。如果你想要详细信息，请继续阅读。否则，跳到摘要部分！

可靠性

完整性不需要太多解释：只要证明者是诚实的，我们提出的所有表达式都应该有效。然而，要证明可靠性，还需要做更多的工作。

和往常一样！

在每一层 i，证明者可能会说谎：

• 在和校验期间发送的多项式。我们知道它们具有次数 1，因此使用 Schwartz-Zippel 引理，证明者在验证者的随机选择中获得成功的概率为 1/ |𝔽| ——本质上与我们这里使用的逻辑相同。
• 直线缩减 q(X)。因为 q(X) 至多是一个 kᵢ ₊₁ 次多项式，我们可以再次使用 Schwartz-Zippel 引理，并计算随机巧合在 r* 的选择中最多为 $kᵢ$ ₊₁ /| 𝔽 | 的概率.

Once caught in a lie on a given layer, the prover must continue to the next layer with an incorrect claim. They’d need to get lucky at every subsequent layer to avoid detection. Which means that for the full circuit, the total soundness error is the sum of the errors at each layer. This results in (d + log₂(S))/ | 𝔽 |.What can we make out of this value? Essentially, that we can make this error arbitrarily small with an adequate selection of 𝔽! In other words, the bigger the size of 𝔽, the smaller the soundness error will be.

一旦在一层上发现谎言，证明者必须继续到下一层，并带有不正确的声明。他们需要在每个后续层都幸运，以避免被发现。这意味着对于完整电路，总的可靠性误差是每一层误差的总和。这导致了 (d + log₂(S))/ | 𝔽 |。我们能从这个值中得出什么结论？基本上，我们可以通过充分选择 𝔽 来使这个误差任意小！换句话说，𝔽 的大小越大，可靠性误差就越小。

所以 GKR 协议是可靠的！

成本

另一个需要讨论的重要方面是完整协议的计算成本。这将决定该协议是否有任何用处。

然而，要解释这些成本，我们需要几个我们尚未提出的引理和想法。我不认为将内容继续堆积到这篇文章中是明智的，而且我们将来可能会有机会讨论这个问题。所以，我再次总结一下这些成本：

• 证明者在 O(S³) 时间内运行。
• 验证者，简化一下，在 O(n + d.log₂(S)) 中运行，其中 n 是评估输入层 MLE 的成本。
• 总通信成本为 O(d.log₂(S)) 字段元素。> 当然，了解这些数字的来源非常重要 —— 但我保证，随着我们深入研究这个系列，我们将继续改进我们的估计逻辑！

  现在最重要的是评估应用 GKR 协议时的验证时间增益。请注意，证明者非常慢：立方时间意味着即使对于不太大的电路，他们的运行时间也会变得非常大。

  然而，当电路浅时，即其深度 d 很小时，验证者会受益匪浅。

  仅举一些数字：对于大小为 2²⁰ （约 100 万个门）且深度为 d = 20 的电路，证明者将运行大约 10¹⁸ 次操作（这非常昂贵），但验证者运行时间仅约为 10⁶，这要小得多！

  并且通信的字段元素数量甚至更少：只有 400！

虽然这在原则上听起来不错，但事实是，对于大型电路，GKR 的证明者成本仍然高得令人望而却步。这成为其适用性的瓶颈，尤其因为其交互性质。

因此，实际实现侧重于某些优化，或将证明者成本降低到更易于管理的水平的预处理步骤 —— 但，朋友们，这将是另一个故事了。

总结

我的天啊。这太长了。

但是我们做到了！

不，朵拉。这不好玩。

我们刚刚看到了第一个真正通用的电路验证协议。尽管存在运行时限制，但 GKR 揭示了一些非常重要的东西：快速验证 任意计算 是可能的。

这是我们走向更实用协议的关键垫脚石。我们未来的目标是找到更好的方法来编码和验证计算，但至少我们现在知道可以做到。

我认为这是我们旅程中一个重要的时刻。我邀请你花点时间来欣赏我们仅用几个工具就完成了多少工作。想象一下我们以后会遇到什么疯狂的事情！

说到这，到目前为止，我们只关注电路作为我们通用计算模型。我不知道你怎么想，但对我而言，编写电路感觉不是编写程序时最自然的事情。我们通常用其他术语来考虑计算。

那么，这是否意味着我们的努力从根本上存在缺陷？这是我们将在下次见面时尝试回答的问题！

下次见！

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～