预测市场中等待期权价值：交易量时机、入场时机和潜在毒性的结构性理论

预测市场会聚合信息。它们也塑造了何时参与是理性的。

你可以在数据中看到它。绘制成交量何时出现，以及市场如何陷入时间机制。有些早早交易并趋于平缓。另一些则保持安静，然后在临近结束时激增。

首先想到的解释是：“新闻在政治中来得晚；体育赛事则更早知晓。”

这种解释很快就站不住脚了，因为同样的晚成交量曲线可能来自不同的机制。人们可能在等待安全。除非你掌握信息或速度很快，否则提前入场可能带来负的预期收益（EV），因此不知情的参与者会推迟。

这两个世界都很重要。一个市场看起来很安静，可能是因为它在等待公开披露，或者因为它通过逆向选择来惩罚提前入场。

这篇文章建立了一个框架，仅使用已结算的链上交易来分离这些力量。它形式化了基本要素，定义了一个基于尾部的指标（从模型中剔除），并解释了为什么一些“体育”市场（拳击）与“新闻”聚集在一起，即使类别标签另有说明。

---

1. 野生环境中的时间机制

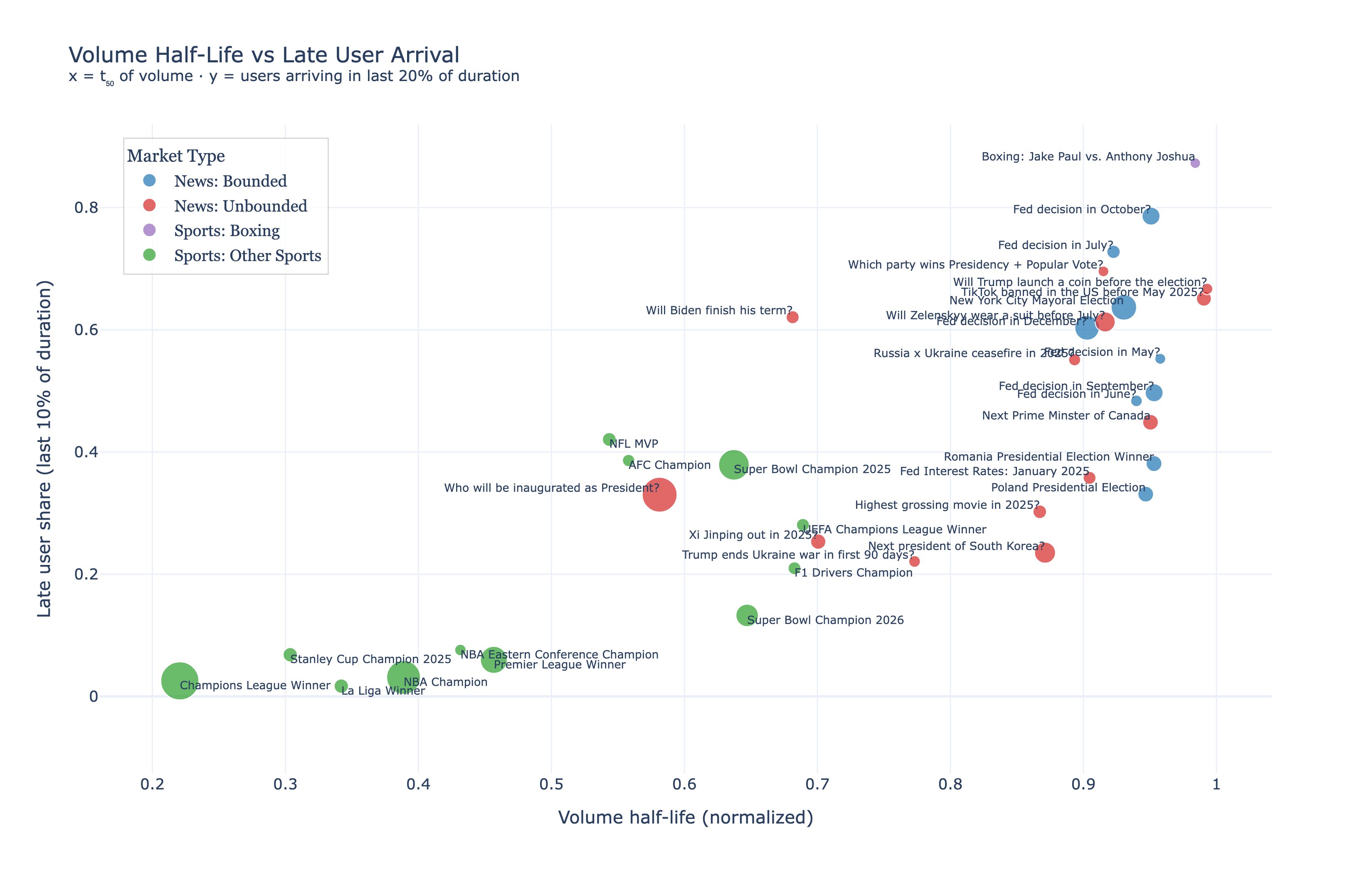来源: Danning 的散点图, https://x.com/sui414/status/2016387824757465131

标题: X轴：成交量半衰期 $t_{50}$，累积成交量 $V(t)=0.5$ 时的归一化时间。 Y轴：后期首次进入份额，即首次交易发生在临近结束的尾部窗口中的钱包比例（例如，市场持续时间的最后 10-20%，如在图表中定义）。 每个点代表一个市场；颜色表示类别。

这张图提出了一个难题。有些市场的成交量出现较晚，有些市场的参与者进入较晚，有些类别的行为与它们的标签不符。本文的其余部分解释了这张地图，而不依赖于类别名称。

---

2. 市场作为一个归一化的时间实验

市场有不同的持续时间，因此我们对时间进行归一化。

设 $s$ 表示时钟时间（链上时间戳）。考虑一个在 $s{\text{open}}$ 开放并在 $s{\text{res}}$ 结算的市场。定义归一化时间：

$$ t=\frac{s-s{\text{open}}}{s{\text{res}}-s_{\text{open}}}\in[0,1]. $$

现在，每个市场都变成了一个单位区间实验。

从已结算的交易中，我们可以构建两个在图表中看起来相似但具有不同经济意义的累积过程。

2.1 累积成交量过程

设 $V(t)\in[0,1]$ 为在时间 $t$ 之前执行的总交易量的比例：

$$ V(0)=0,\qquad V(1)=1. $$

定义相关的密度：

$$ f_V(t)=\frac{dV(t)}{dt}. $$

2.2 累积进入过程

设 $U(t)\in[0,1]$ 为首次交易发生在时间 $t$ 之前的唯一钱包的比例：

$$ U(0)=0,\qquad U(1)=1, $$

具有进入密度：

$$ f_U(t)=\frac{dU(t)}{dt}. $$

如果现有参与者之间进行交易，即使新钱包很少，成交量也可能很高。进入是一个不同的决定：它是将自己暴露于选择风险的决定。

$V(t)$ 告诉你何时发生活动。$U(t)$ 告诉你何时新参与者愿意进入。它们的差距是我们将要利用的对象。

---

3. 交易是一个内生的时间决定

预测市场头寸在结算时支付。这产生了一个时间选择：现在进入还是稍后进入。

以简化形式写出在时间 $t$ 进入的动机：

$$ \pi(t)=\mathbb{E}[\alpha(t)]-c(t)-r(1-t)-A(t). \tag{1} $$

这里：

• $\alpha(t)$ 是在时间 $t$ 的预期信息优势（优势），
• $c(t)$ 是执行成本，
• $r(1-t)$ 是资金锁定到结算时的机会成本，
• $A(t)$ 是逆向选择惩罚：与更好或更快的信息进行交易的预期损失。

当 $\pi(t)\ge 0$ 时，进入是有吸引力的。当等待的期权价值很高时，等待变得有吸引力，因为 $\mathbb{E}[\alpha(t)]$ 上升或 $A(t)$ 下降到足以证明持有成本是合理的。

为什么即使在干净的市场中也会出现等待？

如果 $r=0$，$c=0$，并且 $A(t)=0$，那么延迟没有成本。交易者可以等到他们的估计是最佳的，这已经将活动推向了最后。一旦你增加了持有成本和成本，等待就会变得昂贵，只有那些等待带来强大好处的市场才会保持急剧的后置。

到目前为止，这听起来仍然像是“晚期信息”。下一个小节展示了为什么这种解释仍然不完整。

---

3.1 两个玩具市场（为什么 LOX 必须存在）

构建两个玩具市场会有所帮助，它们可以产生类似的晚期成交量，但来自不同的经济学。

玩具市场 A：晚期风险，低毒性。

以一个在预定公告时结算的市场为例：利率决定、法院裁决、盈利发布。在公告发布之前，私人优势是有限的。大多数参与者都在等待，因为决定性信息集中在临近结束时。在下面的符号中，风险是后置的，而逆向选择 $A(t)$ 保持很小。这仍然可以产生晚期 $V(t)$：许多交易者在临近结算时进入以避免支付 $r(1-t)$。关键是当活动增加时，新参与者会与它同步出现。在活动分位数时间 $t_q=V^{-1}(q)$，你期望 $U(t_q)\approx q$。这里的晚期成交量来自公共信息的时机，而不是来自选择压力。

玩具市场 B：风险不极端，高毒性。

现在假设事件不是一个单一的清晰揭示。信号逐渐到达：谣言、部分披露、私人联系、解释优势。风险并没有非常集中在 $t=1$ 附近。变化的是 $A(t)$。早期进入变得有风险，因为进入者无法将噪声流量与知情流量分开。一小部分知情或快速的交易者可以在他们自己之间产生大量的成交量，从而在不招募许多新钱包的情况下推动 $V(t)$ 前进。外部人士会延迟，因为 $\pi(t)$ 主要因 $A(t)$ 而被拉低，而不是因持有成本。当你从成交量计算 $t_q$ 时，你会发现比活动建议的进入者更少：$U(t_q)<q$。这个不等式正是第 9 节中 LOX 统计量变为正值的条件。在这个玩具市场中，“晚期”来自选择压力，而不是事件时钟。

这些玩具模型解释了 Danning 的 散点图。一个市场可能会变晚，因为风险来得晚（玩具市场 A），或者因为逆向选择抑制了进入（玩具市场 B）。$V(t)$ 无法区分它们。$U(t)$ 可以。

---

4. 信息到达作为风险过程

现在我们需要“决定性信息来得晚”的语言。

设 $\tau$ 为决定性信息到达的时间（公开或私下）。定义风险率：

$$ h(t)=\frac{f{\tau}(t)}{1-F{\tau}(t)}. \tag{2} $$

以尚未获得决定性信息为条件，$h(t)dt$ 是它在下一刻到达的概率。

后置的 $h(t)$ 意味着不确定性在临近结束时消失。即使逆向选择很小，这本身也可以推动成交量变晚。玩具市场 A 就在这里。

因此，仅凭成交量时机无法识别毒性。

---

5. 逆向选择作为时变毒性

现在是第二种力量。

逆向选择是进入者面临的预期损失，他们无法判断交易对手是否具有卓越的信息或卓越的速度。

在间断信息设置中，$A(t)$ 可能在早期很高，因为进入者无法为与泄密交易的机会定价。它也可能在信息时刻附近飙升，因为信号的离散度暂时达到最大值。

$h(t)$ 和 $A(t)$ 都可以使市场看起来很晚。这就是识别问题。

---

6. 从微观激励到宏观时机曲线

将成交量到达表示为一个点过程，其强度为：

$$ \lambda_V(t)=\lambda_0\exp\big(\beta H(t)-\theta A(t)-r(1-t)\big), \tag{3} $$

其中 $H(t)$ 是累积可用信息的单调变换，与 $h(t)$ 隐含的学习有关。

然后累积成交量为：

$$ V(t)=\frac{\int_{0}^{t}\lambdaV(s)ds}{\int{0}^{1}\lambda_V(s)ds}. \tag{4} $$

这使识别问题变得精确：许多不同的对 $(H(t),A(t))$ 可以生成相同的 $V(t)$。我们需要第二个可观察量。

进入时机提供了它。

---

7. 进入时机作为打破僵局的可观察量

定义进入风险：

$$ g_U(t)=\frac{f_U(t)}{1-U(t)}. \tag{5} $$

定义成交量风险：

$$ g_V(t)=\frac{f_V(t)}{1-V(t)}. \tag{6} $$

如果晚期交易主要由风险驱动，则进入者倾向于大致按活动比例到达。如果晚期交易由选择压力驱动，则进入者延迟的时间超过活动预测的时间。

这种差距激发了我们接下来构建的统计量。

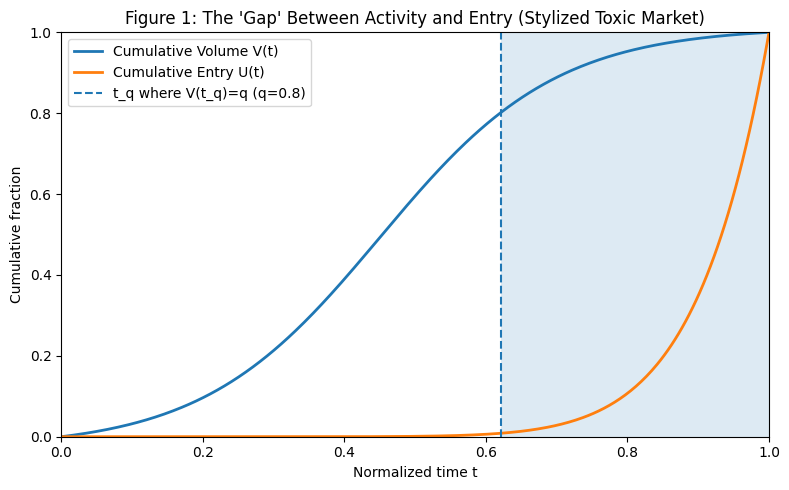
图 1 — 差距图。 绘制了选择性强的市场的 $V(t)$ 和 $U(t)$。$V(t)$ 是一条平滑的 S 曲线。$U(t)$ 保持受到抑制并在后期上升。尾部曲线之间的分离是过度犹豫。

---

8. 尾部事件作为基本要素：在没有时钟截止的情况下定义“晚期”

固定的“最后 20% 或 10% 的时间”窗口在操作上是方便的启发式方法，但它不是一个理论基本要素。市场的活动开始时间不同，因此日历尾部不对齐。

该模型希望通过活动阶段定义尾部。

固定 $q\in(0,1)$。定义活动分位数的截止时间：

$$ t_q \equiv V^{-1}(q), \tag{7} $$

和尾部窗口：

$$ W_q \equiv [t_q,1]. \tag{8} $$

现在，市场通过它们达到相同的活动分数 $q$ 的时间对齐。

定义尾部概率：

$$ L_U(q)=\Pr(\text{首次进入在 }W_q)=1-U(t_q), \tag{9} $$

$$ L_V(q)=\Pr(\text{成交量在 }W_q)=1-V(t_q)=1-q. \tag{10} $$

成交量尾部质量固定在 $1-q$。特定于市场的对象是 $L_U(q)$：有多少进入被压缩到相同的尾部中。

---

9. 衡量过度犹豫：LOX 作为潜在的毒性指数

当进入和活动共同移动时，原始差异 $L_U(q)-(1-q)$ 可能会有噪声。相对度量表现更好。

定义对数几率过度延迟：

$$ \mathrm{LOX}(q)= \log\frac{L_U(q)}{1-L_U(q)}- \log\frac{1-q}{q}. \tag{11} $$

由于 $L_U(q)=1-U(t_q)$，等效地：

$$ \mathrm{LOX}(q)= \log\frac{1-U(t_q)}{U(t_q)}- \log\frac{1-q}{q}. \tag{12} $$

这会将“差距”转换为你可以逐个市场计算的标量。

符号检查

如果进入者相对于活动阶段不成比例地延迟，则 $U(t_q) < q$。这意味着 $1-U(t_q) > 1-q$，这使得 LOX 为正：

$$ U(t_q) < q \quad\Rightarrow\quad \mathrm{LOX}(q)>0. $$

LOX 衡量什么。

选择一个 $q$ 值。查看市场已处理其最终活动的 $q$ 的时刻。询问有多少钱包尚未进入。LOX 将该分数与 $q$ 隐含的基线进行比较。正 LOX 表示“进入滞后于活动”。这是玩具市场 B 产生的足迹。

让我们总结一下解释：

• $\mathrm{LOX}(q)>0$：进入者犹豫的时间超过了活动预测的时间，与高逆向选择一致。
• $\mathrm{LOX}(q)\approx 0$：进入跟踪活动。
• $\mathrm{LOX}(q)<0$：进入者带头进行活动；这可能是由于消费效用或早期定位引起的，并且需要额外的诊断。

---

10. 相图：两个轴，四种机制

LOX 提供了一个微观结构坐标系。

将市场置于二维空间中：

• X 轴：使用 $t_{50}$、$t_q$ 或另一个尾部集中度量来衡量晚期活动。
• Y 轴：使用 $\mathrm{LOX}(q)$ 来衡量过度犹豫。

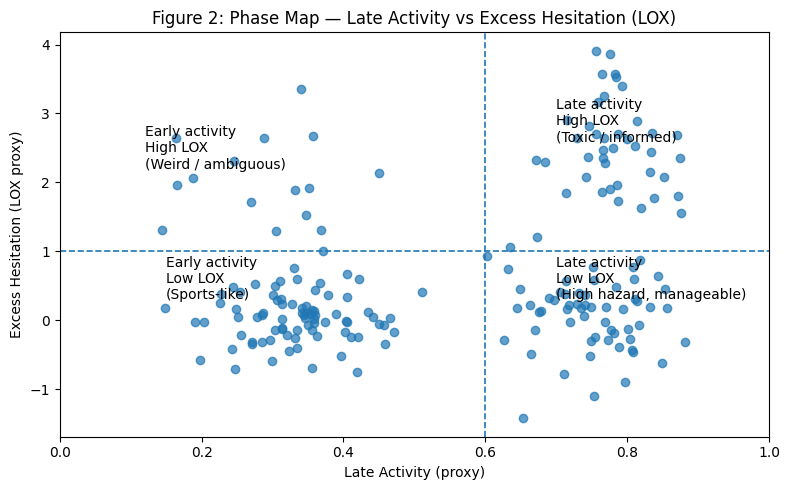
图 2 — 象限图。 在 $(\text{晚期活动},\mathrm{LOX})$ 空间中分散市场：

• 早期活动，低 LOX：类似体育的行为。
• 晚期活动，高 LOX：选择性强的市场（泄密、丑闻、流动性不足）。
• 晚期活动，低 LOX：风险高的市场（晚期新闻，但进入不会异常滞后于活动）。
• 早期活动，高 LOX：罕见情况，通常与结算歧义或特有的微观结构有关。

拳击异常值在这里完美契合。它们落在它们的风险和不对称性放置它们的位置，而不是类别标签放置它们的位置。

---

11. 从已结算的交易中进行估计（无需订单簿）

要计算 LOX，你需要：

• 交易时间戳，
• 交易规模（用于成交量），
• 钱包 ID（用于检测首次进入），
• 市场开放和结算时间。

计算 $V(t)$，计算 $U(t)$，反转 $t_q=V^{-1}(q)$，然后评估 LOX。

为了提高稳健性，计算几个 $q$ 值的 $\mathrm{LOX}(q)$（例如 0.7、0.8、0.9）。选择性强的市场通常显示出随着 $q\to 1$ 而增加的 LOX。

---

12. 可证伪的影响和扩展

一旦你添加了价格序列和有符号的订单流，LOX 就会生成可测试的预测：

高 LOX 市场应该在生命后期显示出更大的晚期标记和更持久的影响。它们还应该显示出晚期进入者之间的利润集中度。

结算时间不确定的市场需要归一化的停止时间版本。结算变得随机，持有成本与风险相互作用，“晚期”变成了一个内生的停止问题。

---

13. 流动性提供：风险风险 vs 选择风险

市场可能以两种方式变晚：

• 高风险：信息来得晚。
• 高 LOX：进入滞后于活动，与逆向选择一致。

对于做市商来说，这些情况感觉不同。

高风险与库存时机有关。高 LOX 与交易对手有关。在高 LOX 市场中，除非将选择溢价计入价格，否则早期报价可能会被系统地选中。

---

14. 结论：时机曲线的真正含义

回到 Danning 的 散点图。

该图表并未将“运动”与“新闻”分开。它分离了不确定性的方式。

有些市场在早期很安静，因为决定性信息来得晚。它们的行为类似于玩具市场 A。它们可能仍然成交量变晚，但进入并没有大大落后于活动。市场正在等待比特，并且大多数参与者都在一起等待。

另一些市场在早期很安静，因为早期的成本很高，除非你有能力在选择中生存。它们的行为类似于玩具市场 B。你仍然可以在早期看到成交量，因为知情或快速的流量可以在它们之间进行交易，但新的进入者会避开。这是 LOX 调整为检测的足迹。

这使得拳击异常值不再那么神秘。拳击不像具有深厚公共先验和稳健的博彩公司参考价格的团队运动那样是“运动”。它通常是一个流动性不足的市场，具有不连续的私人信息（伤害、训练营状况、体重减轻、陪练、最后一刻的医疗或合同事实）。在这种微观结构下，类别标签不再有帮助，而时机统计开始有帮助。

如果你将这些市场视为交易所设计师，那么结论是实用的。你可以观察 LOX 作为参与者基础从广泛的混合流量转变为狭窄的选择性机制的诊断。对于风险控制、激励设计和流动性政策，这比“新闻与运动”更接近于状态变量。

这里 是用于模拟和重现此数学模型中的图形的代码。

---

方法附录：实施说明（来自链上结算的交易）

此附录使 LOX 管道可以从 Dune 风格查询通常公开的最小数据中重现。其逻辑是：在归一化时间内构建两个经验 CDF，一个按成交量加权，一个基于首次进入，并在活动定义的分位数评估它们。

A. 你需要从数据集中获得什么

你需要每个已结算交易（或每个填充）一行。每行应具有：

• market_id
• block_time （时钟时间 $s$）
• trader （钱包地址）
• volume （该市场的一致名义单位）
• 市场元数据：open_time = $s_{\text{open}}$，resolve_time = $s_{\text{res}}$

对 volume 的唯一硬性要求是市场内部的一致性。LOX 使用 $V(t)$ 作为该市场最终总成交量的分数，因此恒定的缩放因子会取消。

有两个边缘案例值得提前决定：

1. 在结算时或之后进行的交易。 如果 block_time > resolve_time，则删除该行或将时间钳制为 resolve_time。否则，$t$ 可能会超过 1，并且曲线停止像 CDF 一样运行。

2. 很少有进入者的市场。 如果一个市场只有少数几个唯一的交易者，$U(t)$ 变得过于粗糙，并且 LOX 由离散性主导。在将 LOX 解释为稳定的市场级别统计量之前，设置最小进入者阈值（例如 50-100）。

B. 归一化时间

对于市场中的每个交易时间戳 $s$，计算：

$$ t=\frac{s-s{\text{open}}}{s{\text{res}}-s_{\text{open}}}. $$

实施细节：将 $t$ 计算为浮点数并裁剪为 $[0,1]$。裁剪可以防止时间戳异常破坏分位数反转。

C. 构建成交量曲线 $V(t)$

按每个市场内的时间 $t$ 对交易量进行排序。

假设交易 $i$ 的成交量为 $v_i$，时间为 $t_i$。定义累积成交量：

$$ \widetilde V(t)=\sum_{i: t_i\le t} v_i, \qquad V(t)=\frac{\widetilde V(t)}{\widetilde V(1)}. $$

根据经验，$V(t)$ 是一个阶梯函数，它从 0 开始，到 1 结束。对于绘图，你可以将时间分成小区间（例如 1% 的区间），并按区间计算累积成交量。LOX 本身不需要平滑处理。

D. 构建进入曲线 $U(t)$

对于市场中的每个钱包 $w$，计算其首次交易时间：

$$ t^{(w)}_{\text{first}}=\min{t_i:\text{ trader}_i=w}. $$

然后定义：

$$ U(t) = \frac{\text{No. of } {w : t^{(w)}_{\text{first}} \le t}}{\text{No. of } {w}} $$

这也是一个阶梯 CDF。分箱可以使图表更易于阅读，但该统计量使用底层经验曲线。

E. 计算 $t_q = V^{-1}(q)$

选择 $q\in(0,1)$。将 $t_q$ 定义为市场已处理其最终成交量的 $q$ 的最早时间：

$$ t_q=\inf{t: V(t)\ge q}. $$

在代码中，这是对累积成交量数组的单调搜索。如果你使用分箱时间，请选择累积部分超过 $q$ 的第一个箱。

此步骤将“最后 20% 或 10% 的时间”替换为“最后 $1-q$ 的活动”，这使得即使在其活动开始时间不同的情况下，市场也可以进行比较。

F. 稳健地评估 LOX

LOX 为：

$$ \mathrm{LOX}(q)= \log\frac{1-U(t_q)}{U(t_q)}- \log\frac{1-q}{q}. $$

数值细节：如果 $U(t_q)$ 在小型市场中恰好为 0 或 1，则对数几率会发散。钳位：

$$ U(t_q) = \min{1-\varepsilon,\max{\varepsilon,U(t_q)}}, $$

使用一个小的 $\varepsilon$（例如 $10^{-6}$）。如果经常对市场进行钳位，则该市场太小而无法使 LOX 稳定。

G. 推荐的诊断

在信任 LOX 值之前，请检查：

• $V(0)\approx 0$ 且 $V(1)=1$（高达容差），
• $U(1)=1$,
• 单调性：两条曲线都应为非递减的，
• $q$ 中的敏感性：以多个 $q$ 值计算 LOX，并查找一致的模式。选择性强的市场通常显示出随着 $q$ 移向 1 而增加的 LOX。

如果你稍后添加价格数据，则下一个自然的诊断是在进入时间上调节的标记：高 LOX 市场中的晚期进入者应具有比早期进入者系统地更好的交易后结果，并且差距在临近结算时最大。

H. 用于模拟和图形的代码

你可以在 这里 找到用于模拟和重现以上图形的代码。

import numpy as np
import matplotlib.pyplot as plt

def logistic(t, k=10.0, x0=0.5):
    """Smooth S-curve in [0,1]."""
    y = 1.0 / (1.0 + np.exp(-k * (t - x0)))
    # Normalize to (approximately) hit 0 and 1 at endpoints
    y0 = 1.0 / (1.0 + np.exp(-k * (0.0 - x0)))
    y1 = 1.0 / (1.0 + np.exp(-k * (1.0 - x0)))
    return (y - y0) / (y1 - y0)

def delayed_j(t, power=12):
    """Sharp J-curve: near 0 for most of time, jumps near 1."""
    return t**power

## -------------------------
## Figure 1: Gap Chart
## -------------------------
t = np.linspace(0, 1, 400)

V = logistic(t, k=8.0, x0=0.45)  # activity accumulates smoothly
U = delayed_j(t, power=10)       # entrants delay heavily

fig, ax = plt.subplots(figsize=(8, 5))
ax.plot(t, V, linewidth=2, label="Cumulative Volume V(t)")
ax.plot(t, U, linewidth=2, label="Cumulative Entry U(t)")

## Highlight tail window for a chosen q
q = 0.8
idx = np.searchsorted(V, q)
idx = min(max(idx, 0), len(t) - 1)
t_q = t[idx]

ax.axvline(t_q, linestyle="--", linewidth=1.5, label=f"t_q where V(t_q)=q (q={q})")
ax.fill_between(t, 0, 1, where=(t >= t_q), alpha=0.15)

ax.set_title("Figure 1: The 'Gap' Between Activity and Entry (Stylized Toxic Market)")
ax.set_xlabel("Normalized time t")
ax.set_ylabel("Cumulative fraction")
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.legend()
plt.tight_layout()
plt.show()

## -------------------------
## Figure 2: Quadrant Scatter (Synthetic)
## -------------------------
rng = np.random.default_rng(7)

## X: late activity proxy (e.g., t_50 or tail concentration) in [0,1]
## Y: LOX proxy (synthetic) in roughly [-2, 4]
sports_x = rng.normal(0.35, 0.08, size=80)
sports_y = rng.normal(0.1, 0.4, size=80)

late_lowtox_x = rng.normal(0.75, 0.07, size=60)  # late activity, low LOX
late_lowtox_y = rng.normal(0.2, 0.5, size=60)

toxic_x = rng.normal(0.78, 0.06, size=40)        # late activity, high LOX
toxic_y = rng.normal(2.5, 0.7, size=40)

weird_x = rng.normal(0.30, 0.08, size=15)        # early activity, high LOX
weird_y = rng.normal(2.0, 0.6, size=15)

X = np.clip(np.concatenate([sports_x, late_lowtox_x, toxic_x, weird_x]), 0, 1)
Y = np.concatenate([sports_y, late_lowtox_y, toxic_y, weird_y])

fig, ax = plt.subplots(figsize=(8, 5))
ax.scatter(X, Y, alpha=0.7)

## Visual quadrant guides
ax.axvline(0.6, linestyle="--", linewidth=1.2)
ax.axhline(1.0, linestyle="--", linewidth=1.2)

ax.text(0.15, 0.3, "Early activity\nLow LOX\n(Sports-like)", fontsize=10)
ax.text(0.70, 0.3, "Late activity\nLow LOX\n(High hazard, manageable)", fontsize=10)
ax.text(0.70, 2.6, "Late activity\nHigh LOX\n(Toxic / informed)", fontsize=10)
ax.text(0.12, 2.2, "Early activity\nHigh LOX\n(Weird / ambiguous)", fontsize=10)

ax.set_title("Figure 2: Phase Map — Late Activity vs Excess Hesitation (LOX)")
ax.set_xlabel("Late Activity (proxy)")
ax.set_ylabel("Excess Hesitation (LOX proxy)")
ax.set_xlim(0, 1)
plt.tight_layout()
plt.show()

---

• 原文链接： github.com/thogiti/thogi...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～