BFT共识中的乐观单轮投票最终性

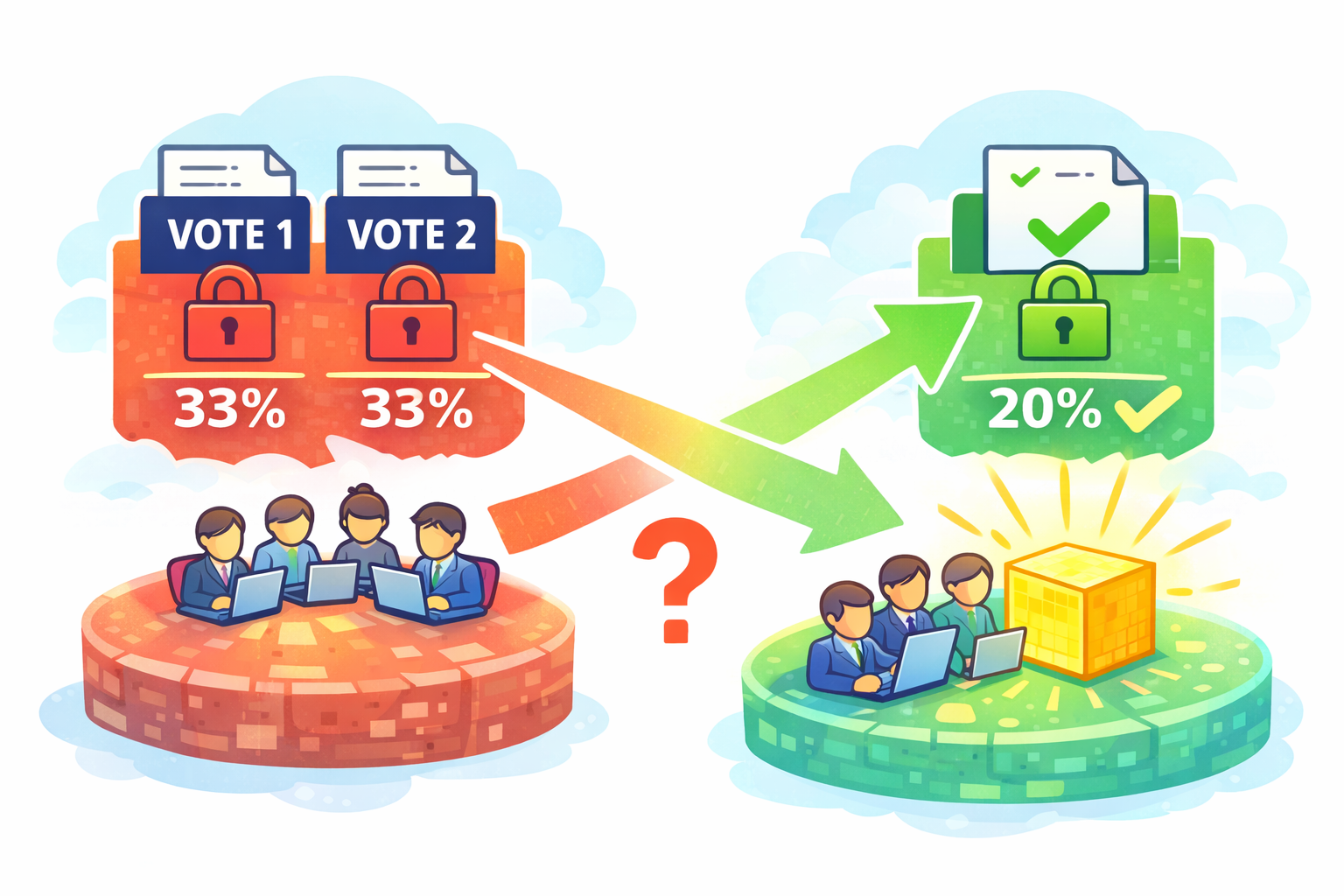
大多数现有的 PoS (Proof of Stake) 区块链使用 BFT (拜占庭容错) 共识协议，该协议假设 33% (或 1/3) 的恶意验证者阈值，并且需要两轮投票（加上一轮提议，总共三轮消息）才能达成最终确认。最近，人们对在 20% 的恶意验证者阈值下进行一轮投票的 BFT 共识（总共两轮消息）重新产生了兴趣，例如 Alpenglow，ChonkyBFT ( zkSecurity 的审计)，以及 Minimmit。这些两轮消息的协议通常实现更快的最终确认，特别是当验证者在地理上分布且网络延迟占主导地位时（这里，消息轮次是单向广播阶段，而不是网络往返）。这篇博客文章解释了一轮投票 BFT 协议背后的直觉，并探讨了乐观的一轮投票最终确认的想法。

我们将建立对以下问题的直觉：

• 为什么大多数现有的 PoS 共识协议假设 33% 的恶意界限（而不是像 50% 这样的）？
• 为什么这些 BFT 协议通常需要两轮投票？
• 何时以及为什么一轮投票实际上是可能的？
• 为什么乐观的一轮投票 BFT 共识是有用的？

基础

让我们从 BFT 共识中的基本设置开始。一组验证者（总共 n 个）协作广播和最终确认区块。它们通过并非总是稳定的网络进行通信，并且一些验证者（总共 f 个）可能恶意行为（在文献中称为拜占庭）。BFT 共识旨在正确地最终确认区块，尽管存在网络不确定性和有故障的参与者。

网络模型。 在现实世界中，网络在大多数时间都快速且稳定。但是，有时它可能不稳定：消息可能会延迟或丢失，并且可能发生网络分区。例如，在平均情况下，你可能期望东京的一台计算机在 200 毫秒内将消息传递到纽约市的服务器。但是，如果你的路由器出现故障或海底电缆被切断，则网络可能会暂时无法访问。这通常被建模为部分同步网络：

网络在一开始是异步的，并且对消息延迟没有限制。在某个未知时间（GST，全局稳定时间）之后，网络表现为同步的，并且对消息延迟有一个已知的限制，但是协议不知道 GST 何时发生。

由于 GST 对验证者来说是未知的，因此他们永远无法确定网络当前是否同步。即使网络看起来健康，它也可能在下一秒钟被中断。结果，当共识算法正在运行时，它必须始终在异步下是安全的。

验证者模型。 大多数验证者是诚实的：它们遵循协议并且不会任意偏离（例如，它们永远不会含糊其辞或重复投票）。当诚实验证者最终确认/提交一个区块时，它会将该决策视为不可逆转的，并且只会构建在已最终确认的历史之上。一些验证者可能会以两种方式出现故障：

• 崩溃故障： 节点可能停止响应，但不会任意行为。如果验证者崩溃或断开连接，则可能发生这种情况。当它恢复在线时，它仍将遵循协议，并且不会恶意行为（例如，它不会重复投票）。
• 拜占庭故障： 节点可能会任意行为，包括保持沉默、含糊其辞或重复提议/重复投票。

BFT 共识协议应具有足够的弹性，以在具有拜占庭验证者的部分同步下维持安全性和活性：

• 安全性： 所有诚实验证者最终都会最终确认相同的区块序列。换句话说，如果诚实验证者遵循协议并提交/最终确认一个区块，则其他诚实验证者也将在该槽位中提交/最终确认完全相同的区块。
• 活性： 在同步期间，协议会取得进展并且不会陷入困境。

安全性确保即使在异步期间也不会发生分叉。活性要求它在同步期间取得进展。

以下是 PoS 区块链中的 BFT 共识通常在高层次上的工作方式：存在一个固定的验证者集合，并且每个验证者都具有基于权益的权重。为简单起见，我们假设相等的权益。验证者之间的所有消息都使用数字签名进行身份验证，以防止伪造。

时间分为槽位，每个槽位都有一个预先指定的领导者（例如，循环）。在每个槽位中，领导者提出一个区块并将其广播给所有验证者。其他验证者验证提案并广播其投票。每个验证者仅对在每个槽位中收到的第一个有效提案进行投票。如果验证者收集到足够的投票，它将提交/最终确认该区块并移至下一个槽位。在将来的槽位中，验证者仅对扩展其最高的已最终确认区块的提案进行投票，因此它永远不会构建与已最终确认的历史冲突的分叉。如果领导者沉默，如果在超时之前没有最终确认区块，则每个验证者都会广播超时消息，而不管它是否在该槽位中投票。一旦达到法定数量的超时，验证者将移至下一个槽位。

33% 的界限

大多数现有的 PoS 区块链都假定有 33% 的拜占庭阈值，并且需要两轮投票才能最终确定区块。 这是因为 1/3 是（非正式地）在部分同步 BFT 协议下可以同时维护安全性和活性的最大拜占庭比例。 让我们看看为什么。

设 n 是验证器的总数，其中最多 f 是拜占庭式的。

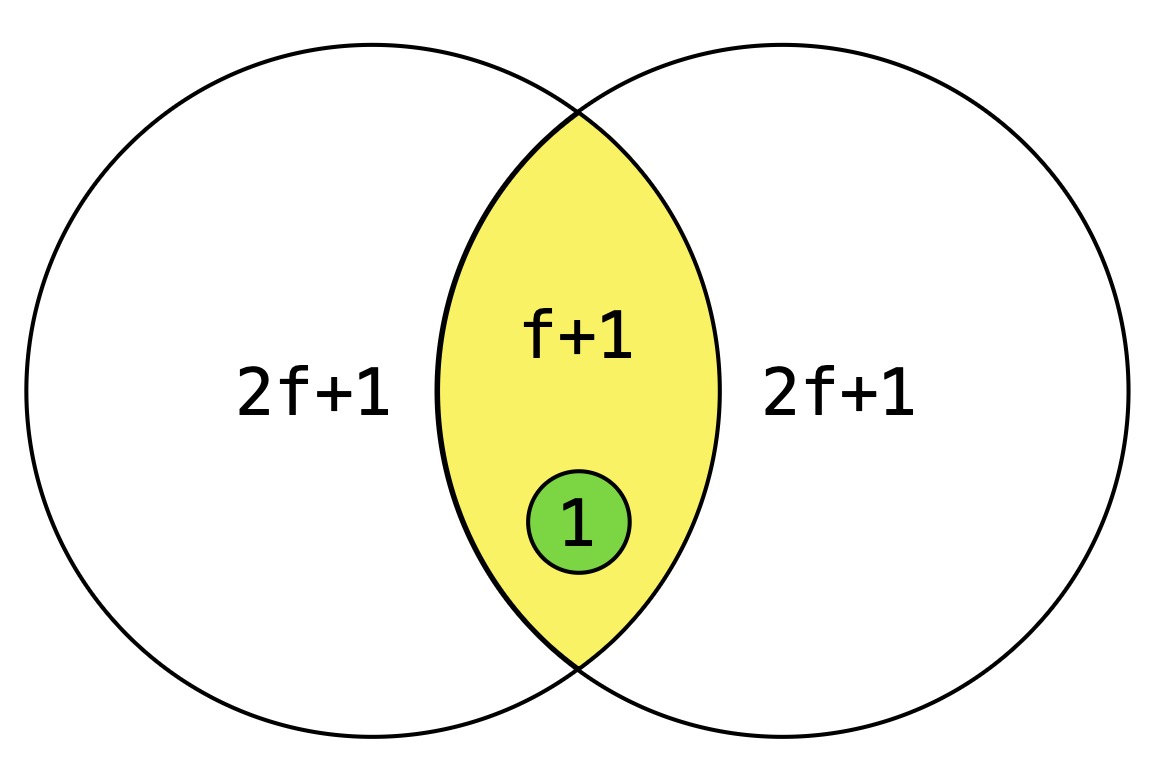
首先，我们介绍一种有用的分析技术，称为法定人数交集：对于每个都具有 x 个验证器的两组，它们至少具有 max(0, 2x - n) 个共同的验证器。 由于这些共同验证器中最多 f 个可能是拜占庭，因此这两组至少具有 max(0, 2x - n - f) 个共同的诚实验证器。 例如，假设 n = 3f + 1，并且我们有两组具有 x = 2f + 1 个验证器。 那么这两组至少重叠 f + 1 个验证器，并且其中至少 1 个必须是诚实的。 如果两个冲突的提案在某个插槽中都获得 2f + 1 个投票（因此都达到法定人数），那么他们的投票集必须至少重叠一个诚实的验证器，这意味着某些诚实的验证器将不得不对两者都投票，这是不可能的。

现在假设一种共识算法需要来自 x 个验证器的投票才能做出有意义的决定（即，法定人数为 x）。 回想一下，拜占庭验证器可以保持沉默或含糊其辞。

• 活性 要求协议即使在所有 f 个拜占庭验证器保持沉默的情况下也能仅使用诚实的投票来最终确定。 在最坏的情况下，只有 n - f 个验证器可用，因此我们必须具有 x ≤ n - f。 否则，如果我们设置 x = n - f + 1（或更大），那么攻击者可以发起一个微不足道的 DoS：保持所有拜占庭验证器沉默，并且协议将永久地“差一票”才能达到法定人数，并且永远不会取得进展。
• 安全性 要求即使所有 f 个拜占庭验证器都重复投票，也不能同时达成两个冲突的决定。 为了确保在一个插槽中最多只有一个提案可以达到法定人数，我们需要法定人数足够大，以至于任何两个法定人数集都共享至少一个诚实的验证器。 也就是说：2x − n - f > 0，即 x > (n + f) / 2。 在这种情况下，如果两个不同的提案都获得 x 个投票，那么必须存在一个诚实的验证者，该验证者对这两个提案都进行了投票，这是不可能的。

结合两个方向，我们需要：

$(n+f)/2 < x ≤ n−f$

为了使这样的 x 存在，我们需要：

$(n+f)/2 < n−f ⇒ f < n/3$

这正是拜占庭验证器必须少于总数的三分之一的说法！

直观地，1/3 是最大的拜占庭比例，在该比例下，我们可以选择一个足够大的法定人数来强制诚实重叠（安全性），但又足够小以仅用诚实的投票即可到达（活性）。 这就是为什么许多 PoS 区块链都假定一个 33% 的拜占庭阈值：这是他们可以定位的最大弹性界限。

最小的整数选择是 n = 3f + 1。 在这种经典设置中，选择 x = 2f + 1 满足双方：

• 活性：$2f + 1 ≤ n − f = 2f + 1$。
• 安全性：$2x − n = (4f + 2) − (3f + 1) = f + 1 > f$。

在这种情况下，如果区块 B1 和一个冲突的区块 B2 在 3f + 1 个验证器中都收到 2f + 1 个投票，那么它们的投票集必须至少重叠 f + 1。 在最多 f 个拜占庭验证器的情况下，至少一个重叠的投票者是诚实的，这意味着诚实的重复投票，这是不可能的。 因此，两个冲突的区块不能都达到 2f + 1。

请注意，1/3 是最大阈值。 当然，在设计协议时，我们可以假设一个较低的阈值，例如 n = 5f + 1（即 20%）。 在那种情况下，3f + 1 ≤ x ≤ 4f + 1 范围内的所有 x 都是有效的法定人数。 正如我们将看到的，较低的拜占庭阈值是将两轮投票减少到一轮的关键。

两轮投票

乍一看，当 n = 3f + 1 时，我们似乎只需要一轮投票：在每个插槽中，领导者提出一个区块，验证器验证它，广播一个投票，并且任何收集 2f + 1 个投票的验证器立即最终确认该区块。 在单个插槽中，这看起来是安全的，因为在同一插槽中，没有冲突的区块可以达到 2f + 1 个投票。 但是，如果插槽超时，该区块仍然可以“丢失”。

考虑以下情况：所有 f 个拜占庭验证器都保持沉默。 2f 个诚实验证器投票支持区块 B。 最后一个诚实验证器也投票支持 B，并且在本地看到 2f + 1 个投票，因此它最终确定了 B。 但是由于网络异步，它未能将其投票交付给其余验证器。 结果，其他验证器永远不会知道 B 达到了 2f + 1 个投票。 当插槽超时时，下一个领导者可以提出一个跳过 B 的区块。 在这种情况下，一个诚实验证器提交 B，而其他验证器跳过它。 安全性受到侵犯。 问题在于 2f + 1 个投票仅保证 B 是可以在该插槽中提交的唯一候选者，但它不能保证该插槽不会被跳过。

我们添加第二轮投票，以在第一轮之后进一步决定插槽结果是“提交 B”还是“空”（受此博客文章的启发）：

• 第一次投票 (vote1)：在验证器看到领导者的提议 B 并认为其有效后，它会广播 vote1(B)。
• 第二次投票 (vote2)：如果验证器观察到区块 B 的 2f + 1 个 vote1，则它会广播 vote2，其中包含它收集的 vote1(B)。 在收到 2f + 1 个 vote2 之后，验证器提交区块 B 并移至下一个插槽。
• 超时 (timeout)：如果验证器在超时后尚未在此插槽中提交一个区块，则它将广播 timeout。 如果验证器已发送 vote1 或 vote2，则它会将它们包含在超时消息中：timeout(vote1, vote2)。 在看到 2f + 1 个 timeout 消息后，验证器将移至下一个插槽。

如果一个诚实的验证器提交了一个区块，那么它必须已经看到了 2f + 1 个 vote2。 通过法定人数交集，任何一组 2f + 1 个 timeout 消息必须在至少一个诚实的验证器中与任何一组 2f + 1 个 vote2 消息相交。 这意味着，如果下一个领导者收集 2f + 1 个 timeout，则这些 timeout 消息中至少有一个包含 vote2，而 vote2 又包含 2f + 1 个 vote1。 因此，上一插槽的区块不能“丢失”：该协议可以要求下一个领导者扩展它，并且诚实的验证器将拒绝投票支持不扩展已锁定区块的提议。

需要第二轮投票来维持跨插槽的安全性。 直观上，这是从验证器的角度来看的：

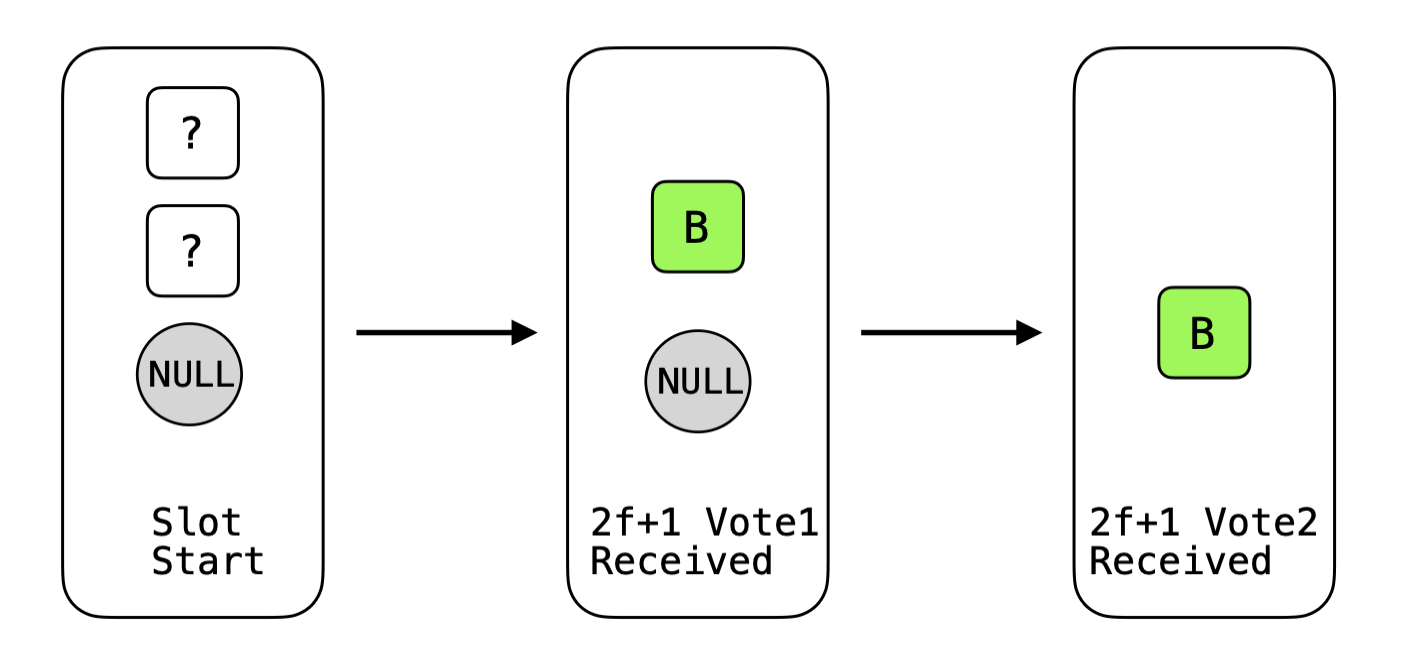
• 在插槽开始时，在达到法定数量的 vote1 之前，验证器无法确定将最终确定哪个区块（如果有）。
• 在收集到 B 的 2f + 1 个 vote1 之后，插槽的结果为“B 或空”（没有冲突的区块也可以收集 2f + 1）。
• 在收集到 B 的 2f + 1 个 vote2 之后，B 无法在以后的插槽中跳过，因此可以安全地最终确定。 所有诚实的验证器最终也会了解到这一点并最终确定 B。

一轮投票

我们现在知道，当 n = 3f + 1 时，我们需要第二轮投票，因为 2f + 1 个 vote1 不足以在“区块 B”和“空”之间做出决定。 一个自然的问题是：如果验证器在第一轮中获得超过 2f + 1 个区块 B 的 vote1，那么额外的投票是否提供更多的确定性？ 答案是肯定的：如果验证器在第一轮中收集所有投票 (3f + 1)，则它可以直接提交一个区块。

假设，在某些插槽中，拜占庭验证器的行为是诚实的（稍后会详细介绍）。 验证器会收集区块 B 上的所有 3f + 1 个 vote1。 那么在该插槽中不可能有另一个有效区块收集法定人数的投票。 我们仍然需要确保 B 不会被跳过：任何一组 2f + 1 个 timeout 消息都必须在至少 f + 1 个诚实验证器中与 3f + 1 个 vote1 消息相交。 这意味着，在 2f + 1 个超时中，至少有 f + 1 个包含 vote1(B)，这是一个严格的多数。 因此，下一个领导者（收集 2f + 1 个超时）被迫扩展 B。 因此，在收到所有 3f + 1 个 vote1 之后，可以安全地进行最终确定，因为额外的投票可确保该区块不会被跳过。 相反，收到更少的 vote1（例如 3f）是不够的，因为它不能保证 vote1(B) 构成超时法定人数内的多数。

这产生了一条快速通道，可以在看到 3f + 1 个 vote1 后仅在一轮投票中最终确定一个区块。 它是乐观的，因为它要求所有 f 个拜占庭验证器在该插槽中诚实地参与。 任何拜占庭验证器都可以通过 withholding 其投票来阻止快速通道。 我们仍然需要第二轮通道作为默认的安全通道。

如果我们想要一轮最终确认，而不对拜占庭参与持“乐观”态度，我们需要一种避免依赖拜占庭投票的方法。 事实证明，解决方案非常简单：降低容忍的拜占庭比例，以便我们可以拥有更多的诚实验证器。

假设 $n >= 3f + 1$。 让验证器在看到 n - f 个 timeout 后移至下一个插槽。 让验证器在看到 n - f 个 vote1 后最终确定一个区块（我们可以在不依赖拜占庭验证器的情况下保证的最大投票数）。 那么这些 vote1 和 timeout 集合的诚实交集至少为 n - 3f（因为 (n-f) + (n-f) - n - f = n - 3f）。 为了强制执行该区块不能被跳过，该区块的 vote1 在超时法定人数内必须是严格的多数：

$n−3f>(n−f)/2 ⇒ n>5f$

这说明当 $n > 5f$ 时，我们可以实现稳定的一轮最终确认（在同步期间不依赖拜占庭验证器），即当拜占庭验证器少于 20% 时！

当 n = 5f + 1 时，它看起来像这样：

• 第一次投票 (vote1)：在验证器看到领导者的提议 B 并认为其有效后，它会广播 vote1(B)。 如果验证器看到 4f + 1 个 vote1，它将直接最终确定该区块并移至下一个插槽。
• 超时 (timeout)：如果验证器在超时后尚未在某个插槽中提交一个区块，则它将广播 timeout。 如果验证器已发送 vote1，则它会包含它：timeout(vote1)。 在看到 4f + 1 个 timeout 消息后，验证器将移至下一个插槽。

如果一个诚实的验证器提交了一个区块，那么它必须已经看到了 4f + 1 个 vote1。 通过法定人数交集，任何一组 4f + 1 个 timeout 消息必须在至少 2f + 1 个诚实验证器中与任何一组 4f + 1 个 vote1 消息相交（因为 (4f+1) + (4f+1) - (5f+1) - f = 2f+1)，这是一个严格的多数。 因此，如果下一个领导者收集 4f + 1 个超时，则其中一半以上包含 vote1(B)，从而迫使领导者扩展 B。

这就是最近的协议（如 Alpenglow 和 Minimmit）如何以 20% 的拜占庭阈值实现一轮最终确认的直觉。 这将三个消息轮次减少到两个，这有意义地减少了最终确认延迟，特别是对于地理上分布的验证器，其中网络延迟（一个轮次消息约为 100 毫秒）占主导地位。 这些协议通常也更容易推理，因为它们避免了第二种类型的投票。

请注意，我们仍然可以在共识中保留两轮回退。 一轮和两轮路径可以同时运行。 在该设计中，两轮路径的法定人数阈值可以是 x = 3f + 1（即 60%），以便两个法定人数在至少一个诚实验证器中相交。 这意味着两轮路径只需要 60% 的诚实参与即可达成最终确认。 它可以容忍另外 20% 的诚实节点崩溃，同时保持安全性和活性。 这就是围绕 Solana 的 Alpenglow 设计的“20% 拜占庭 + 20% 崩溃”框架背后的直觉。

在一轮和两轮之间：乐观的一轮最终确认

在 33% 的拜占庭阈值下，我们通过两轮投票实现最终确认； 在 20% 的拜占庭阈值下，我们通过一轮投票实现最终确认。 现在考虑拜占庭阈值介于 20% 和 33% 之间的中间情况。

假设 $n >= 3f + 1$，并且我们使用与先前相同的协议结构。 我们知道，两轮路径的法定人数为 $x > (n+f)/2$。 假设一轮最终确定阈值为 y。 为了在一轮中最终确定，我们需要足够的 vote1，以使 n-f 个 timeout 消息中有一半以上包含该区块的 vote1。 使用相同的交集推理：

$y+(n−f)−n−f>(n−f)/2 ⇒ y>(n+3f)/2$

如上所述，我们可以同时运行这两个路径：在第一轮之后，如果验证器收集 x 个 vote1，则它会广播 vote2 并继续收集 vote1。 在收集 y 个 vote1 之后，它将立即最终确定该区块。

当拜占庭阈值从 20% 增加到 33% 时，一轮投票最终确定阈值 y 从 80% 增加到 100%，这始终大于保证的诚实参与 n - f（从 80% 增加到 66%）。 在该范围内，一轮投票最终确定必然依赖于某些拜占庭验证器的投票来触发，因此它变得乐观。 下表列出了不同拜占庭阈值下的最终确定阈值。

例如，当拜占庭阈值为 30% 时，我们可以通过大约 65% 的投票实现两轮投票最终确认，并通过大约 95% 的投票实现一轮投票最终确认。 这以仅将最坏情况下的拜占庭阈值从 33.3% 降低到 30% 的代价，提供了一条可行的一轮快速通道。

这种乐观的快速通道想法已在先前的著作Fast Byzantine Consensus中进行了研究，并且在最近的著作中也进行了研究，例如Kudzu和Hydrangea。 但是，它尚未得到广泛的生产采用。 有人可能会认为乐观的快速通道不太有用，因为“依赖拜占庭验证器做正确的事”听起来是矛盾的。 但是，实际上，它可以成为一种在不牺牲保守的最坏情况安全性下降低最终确认延迟的实用方法，因为：

• 在 PoS 协议中，拜占庭阈值是一个最坏情况安全假设：它指定了协议旨在容忍同时保持安全性和活跃性的最大对抗性权益。 协议通常选择保守的界限（例如，1/3）作为纵深防御基线，但这并不意味着系统会持续以该界限运行。 实际上，有效的对抗性权益通常较低，因此更大的诚实权益参与给定插槽并解锁快速通道是可行的。 从这个意义上讲，快速通道对实际情况比最坏情况更好持“乐观”态度。
• 拜占庭行为不是静态特征； 这是一个插槽选择。 在长期运行的 PoS 区块链中，验证器在经济上受到激励以正确行为，并且通常会因可检测到的不当行为（例如，含糊不清和不活动）而受到惩罚。 跨许多连续插槽的持续对抗行为可能代价高昂，并增加了检测和惩罚的风险。 结果，即使协议必须容忍高达最坏情况量的拜占庭权益，也可以合理地预期许多插槽会表现出较轻的对抗行为，从而使一轮乐观的最终确认更有可能在稳定状态下触发。

例如，以太坊和 Solana 在实践中都具有非常高的参与度（以太坊参与度约为 99%+，Solana 投票成功率约为 99%+，来自Rated），远好于最坏情况的假设：

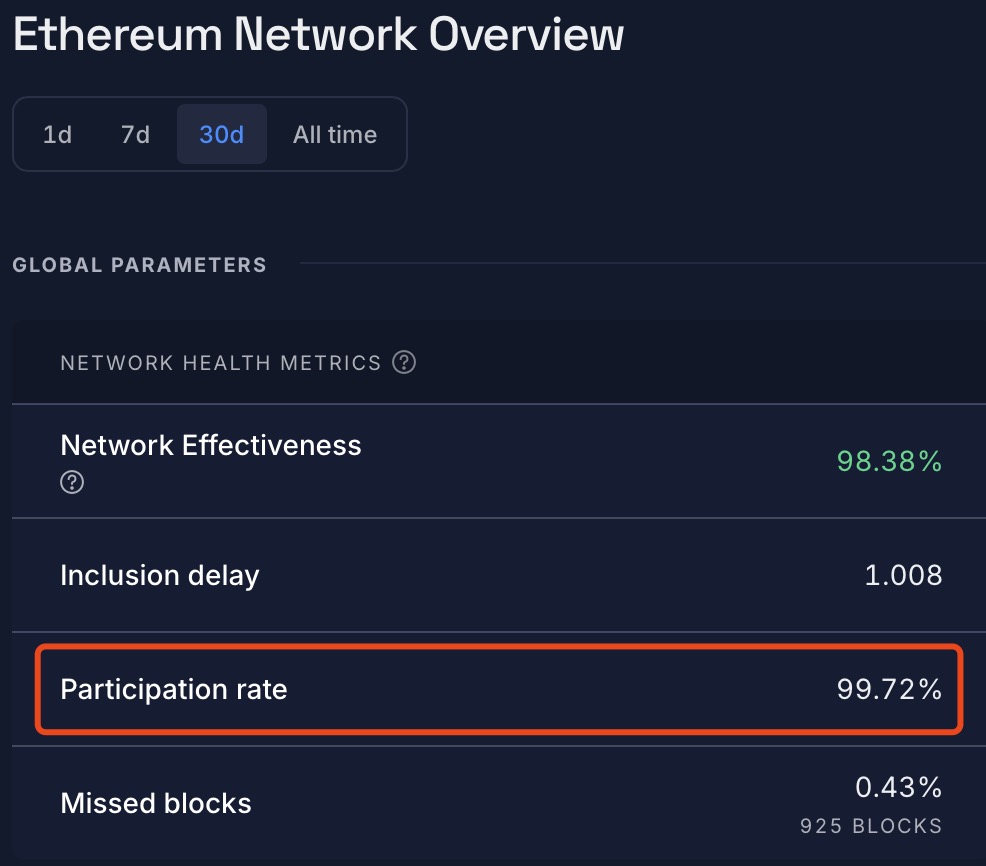
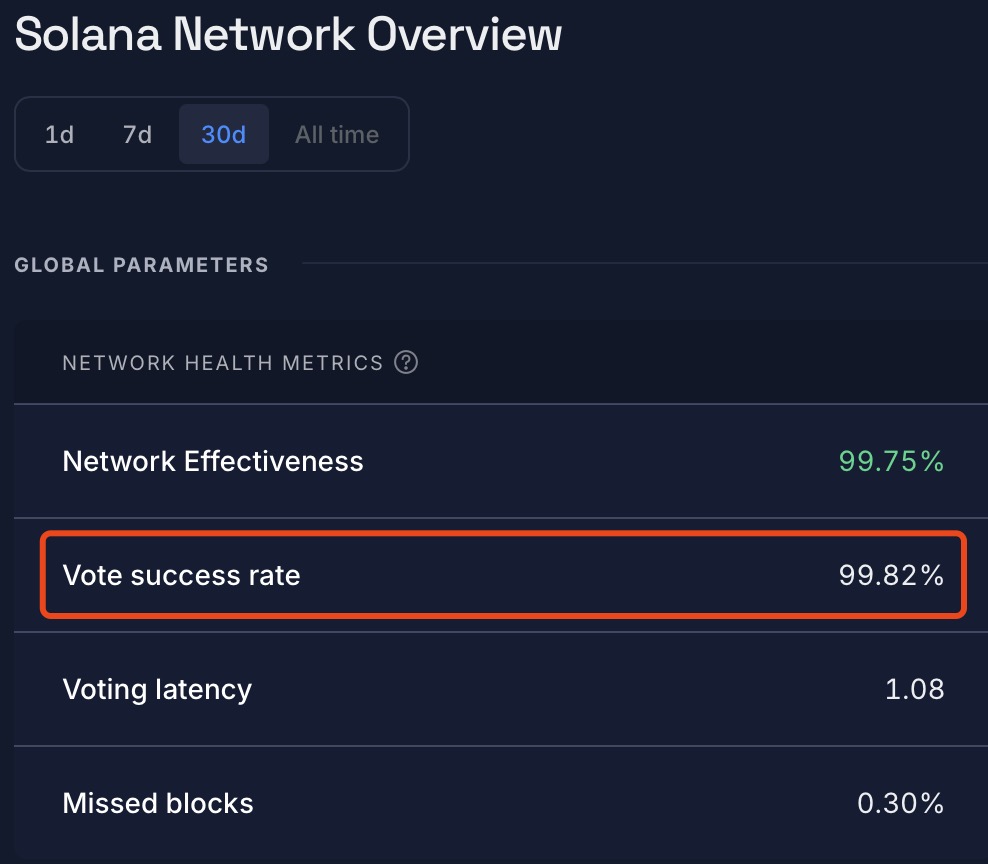
以太坊目前使用两轮投票风格的最终确认，因此区块需要两个时期（约 12.8 分钟，每个时期约 6.4 分钟）才能最终确认。 凭借实践中的高投票率，通过将拜占庭阈值降低到约 30% 并添加乐观的一轮投票快速通道，在技术上可以定位到一个时期最终确认。

这个想法是防御最坏情况，同时优化常见情况：两轮投票是保守的基线，旨在在最坏情况下的网络和对抗性假设下保持安全和存活。 一轮路径可以用作分层在保守基线之上的乐观快速通道。 当某个插槽的条件好于最坏情况时（例如，高参与度和有限的对抗性中断），它可以更早地进行最终确定，而两轮路径仍然是保留原始弹性的保证的回退方案。

结论

大多数 PoS 区块链都假设 33% 的拜占庭阈值，因为它是部分同步 BFT 共识的经典上限。 在这种设置中，需要两轮投票来确保跨插槽的安全性。 最近的一些 BFT 协议假设 20% 的拜占庭阈值来实现一轮投票最终确认，从而将三个消息轮次减少到两个。 在 20% 到 33% 之间，乐观的一轮投票最终确认是可能的：它需要比保证的诚实阈值更多的投票，因此取决于（某些）拜占庭验证器不中断给定插槽。 尽管如此，作为分层在保守基线之上的快速通道，它可以在实践中降低最终确认延迟，而不会牺牲最坏情况的安全性。 看到更多的区块链探索这个设计空间将是一件有趣的事情。

zkSecurity 为包括零知识证明、MPC、FHE 和共识协议在内的加密系统提供审计、研究和开发服务。

了解更多 →

• 原文链接： blog.zksecurity.xyz/post...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～