借贷协议如何计算利息
- 七哥
- 发布于 2022-11-12 21:27
- 阅读 8571
通过本文学习可掌握计息算法原理,并掌握Compound借贷协议的计息逻辑。
「宇宙间最大的能量是复利,世界的第八大奇迹是复利。」 ——爱因斯坦
因交易成本,在智能合约中无法执行大规模计算。那么借贷协议是如何高效的为每位借贷人计算利息的呢?总不能分别为一万个两万个甚至更多的借款人实时更新利息。下面七哥(公众号“七哥链道”)将同你讲解计息算法,通过本文学习你可掌握计息算法原理,并掌握Compound借贷协议的计息逻辑。
什么是复利
通俗讲,复利就是常说的利滚利。 比如在一段时间内以 10% 的月利率借高利贷 100 元,每月结束依次会产生 10 元、10 元、10 元的单利,但会产生 10 元、11 、 12.1、13.31... 的复利。
计算复利是定期将累积的利息与现有本金合计,然后计算新本金的利息。新的本金等于初始本金加上累积的利息。复利经常按每年、每半年、每季度、每月等定期计算。
设初始本金 $P$,年利率 $R$,时长 $T$(单位:年),每年复利次数 $N$,则到期复利金额 $A 计算公式如下:
$$ \begin{equation} \begin{aligned} A = P (1+ \frac{R}{N})^{NT} \end{aligned} \end{equation} $$
$A$ 是初始本金与累计利息之和。如果每年复利一次,公式可简化为: $$ \begin{equation} \begin{aligned} A = P (1+ R)^{T} \end{aligned} \end{equation} $$
如下图,同样借 100 元,年利率 4.75% ,不同计息方式随着时间推移复利增长得越来约快。复利让利息累积到本金中,使利息随着时间的推移增长得更快,呈指数级增长!还记得国际象棋的棋盘上放米粒的故事吗?背后都是等比数列所展示的威力。
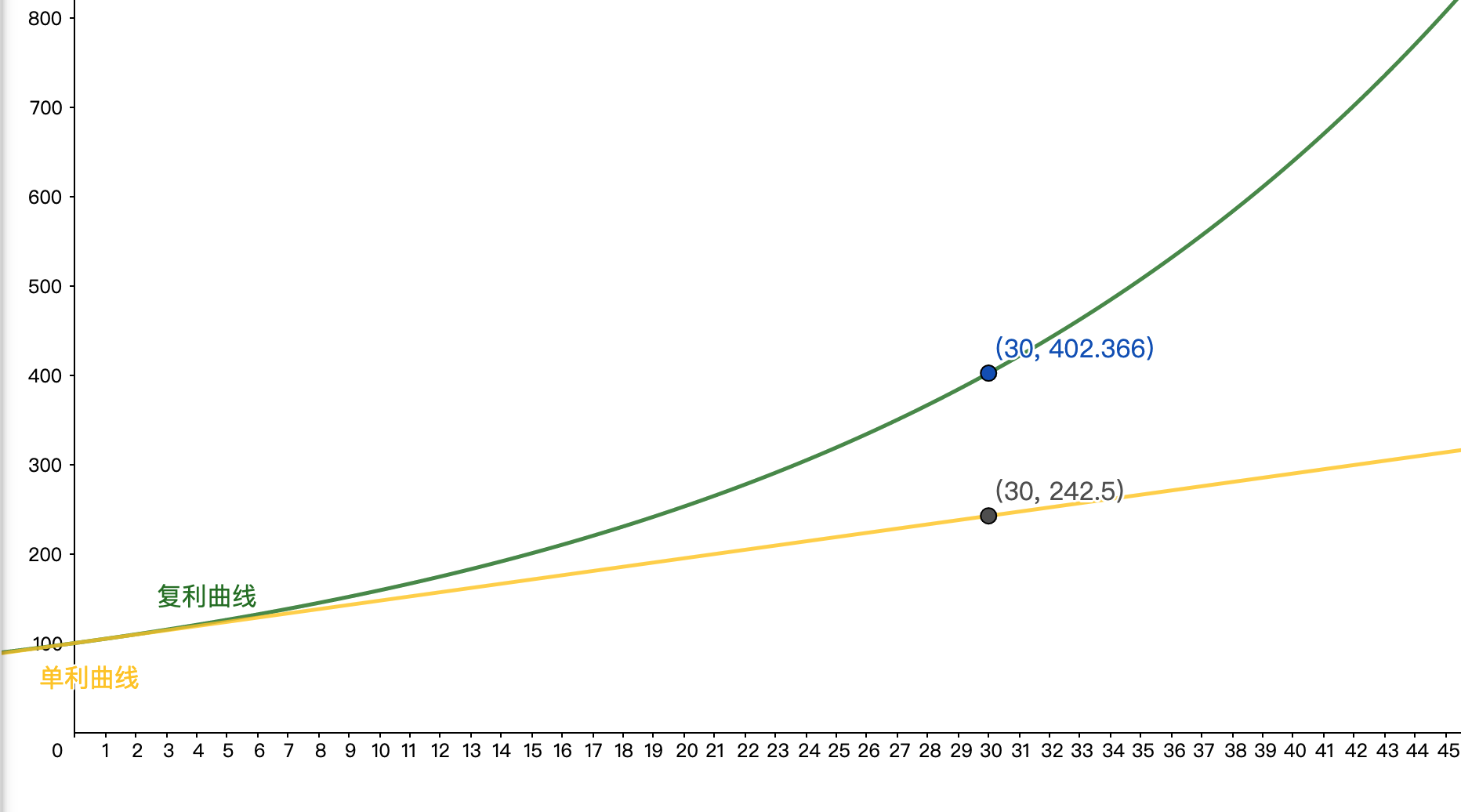
浮动利率怎么办?
在区块链借贷协议中,大部分采用复利方式计算利息,但并非固定利率,而是浮动利率。即每次复利计息时所使用的利率是根据市场借贷供关系决定的。因此,我们并不能使用固定利率公式计算复利,只能根据利率滚动计算,公式如下: $$ \begin{equation} \begin{aligned} A_{t+1}= At(1+R{t+1}) \end{aligned} \end{equation} $$
- $A_{t+1}$ 表示在 $t+1$ 时的复利额。
- $A_t$ 表示 $t$ 时的复利额,是 $ t+1 $ 复利计息时的新本金。
- $R_{t+1}$ 是在 $t+1$ 时刻计算出的利率,表示从 $t$ 到 $t +1$ 时间段内的区间利率。
我们很容易推导出: $$ \begin{equation} \begin{aligned} A_{t+1}&= A_1 (1+R_2)(1+R_3)(1+R_4)(1+R5)...(1+R{t+1}) \ &=P(1+R_1)(1+R_2)(1+R_3)(1+R_4)(1+R5)...(1+R{t+1}) \end{aligned} \end{equation} $$
借一段时间的利息是多少?
现在,我们已经掌握复利计算公式,可问题是不是所有人都是从 0 时刻开始借款,而是在一个不确定的时刻借走的,复利计算时需要知道一段时间的利率是多少。假如七哥在 $t_i$ 时刻借走500万U,在 t_n 时刻还款时连本带息应还多少呢?
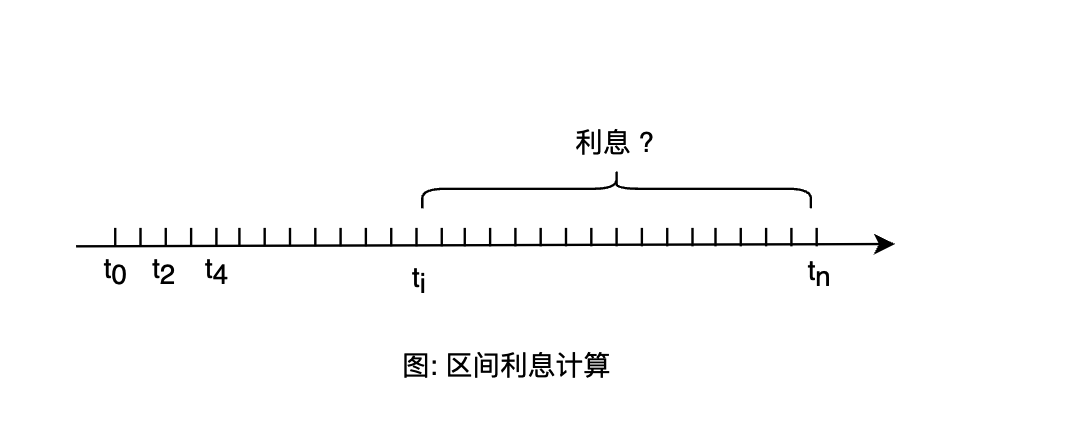
根据公式4可以推导出应还本息公式:
$$ \begin{equation} \begin{aligned} A&= P(1+Ri)(1+R{i+2})...(1+R{n-1})(1+R{n}) \ &=P \frac{ (1+R_1)(1+R_2)(1+R_3)(1+R_4)(1+R5)...(1+R{t+1}) }{ (1+R_1)(1+R2)... (1+R{i-1})(1+R_i) } \end{aligned} \end{equation} $$ 如果把 $ (1+R_1)(1+R_2)...(1+Rt)(1+R{t+1})$ 称之为 $t+1$ 时的累积利率 $\mathcal{R}{t+1}$,则有: $$ \begin{equation} \begin{aligned} A = P \frac{\mathcal{R}{t+1}}{\mathcal{R}_{i}} \end{aligned} \end{equation} $$ 因此,计算本息时只需要知道借款和还款时的累积利率,便可计算出本息额。减去借款本金,剩余部分为借款应付利息。
Compound协议计息方式
有了理论支撑,我们一起看看 Compound 借贷协议是如何计息的。当有人存款、借款、还款、提现、清算时都会先执行一次计息。这相当于不定时的复利,复利频次由市场活跃度决定。如下图,不管张三存款还是李四借款,都会触发计息。
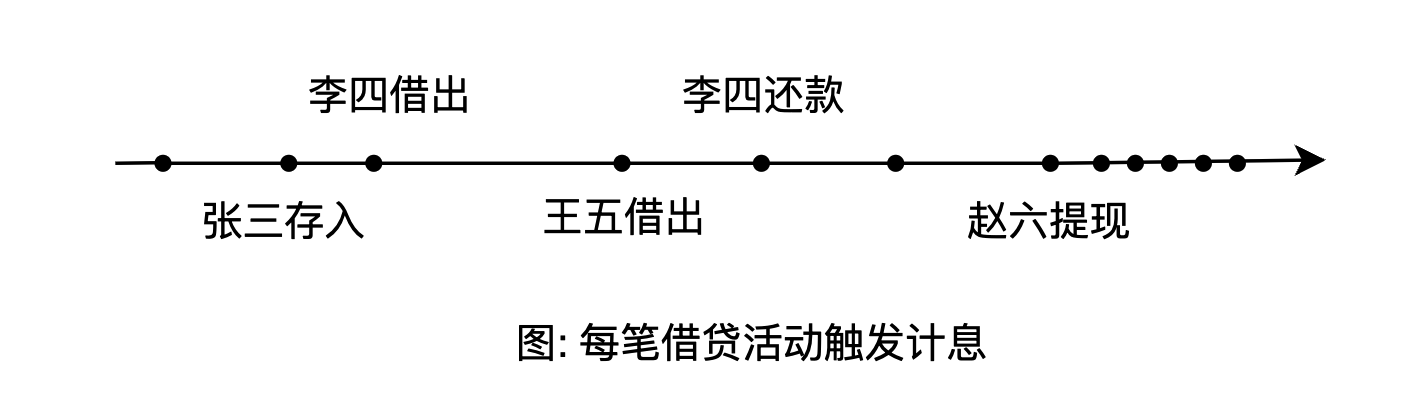
每笔借贷触发计息,在计息时只需要存储当前的累积利率,累积利率在Compound中被称之为 BorrowIndex。Compound计息方法在合约中比较冗余,下方是简化版代码:
function accrueInterest(){
var currentBlockNumber = getBlockNumber(); //获取当前区块高度
//如果上次计息时也在相同区块,则不重复计息。
if (accrualBlockNumber == currentBlockNumber) {
return NO_ERROR;
}
var cashPrior = getCashPrior(); //获取当前借贷池剩余现金流
//根据现金流、总借款totalBorrows、总储备金totalReserves 从利率模型中获取区块利率
var borrowRateOneBlock = interestRateModel.getBorrowRate(cashPrior, totalBorrows, totalReserves);
// 计算从上次计息到当前时刻的区间利率
var borrowRate=borrowRateOneBlock*(currentBlockNumber - accrualBlockNumber);
// 更新总借款,总借款=总借款+利息=总借款+总借款*利率=总借款*(1+利率)
totalBorrows = totalBorrows*(1+borrowRate);
// 更新总储备金
totalReserves =totalReserves+ borrowRate*totalBorrows*reserveFactor;
// 更新累积利率: 最新borrowIndex= 上一个borrowIndex*(1+borrowRate)
borrowIndex = borrowIndex*(1+borrowRate);
// 更新计息时间
accrualBlockNumber=currentBlockNumber;
return NO_ERROR;
}为方便理解代码,请阅读注释部分。最核心部分是 borrowIndex 累积利率的更新计算,在合约中始终记录着最新累积利率。当用户借款时,将存储用户借款金额和此刻的累积利率。如下图演示的是借贷时的计息过程。
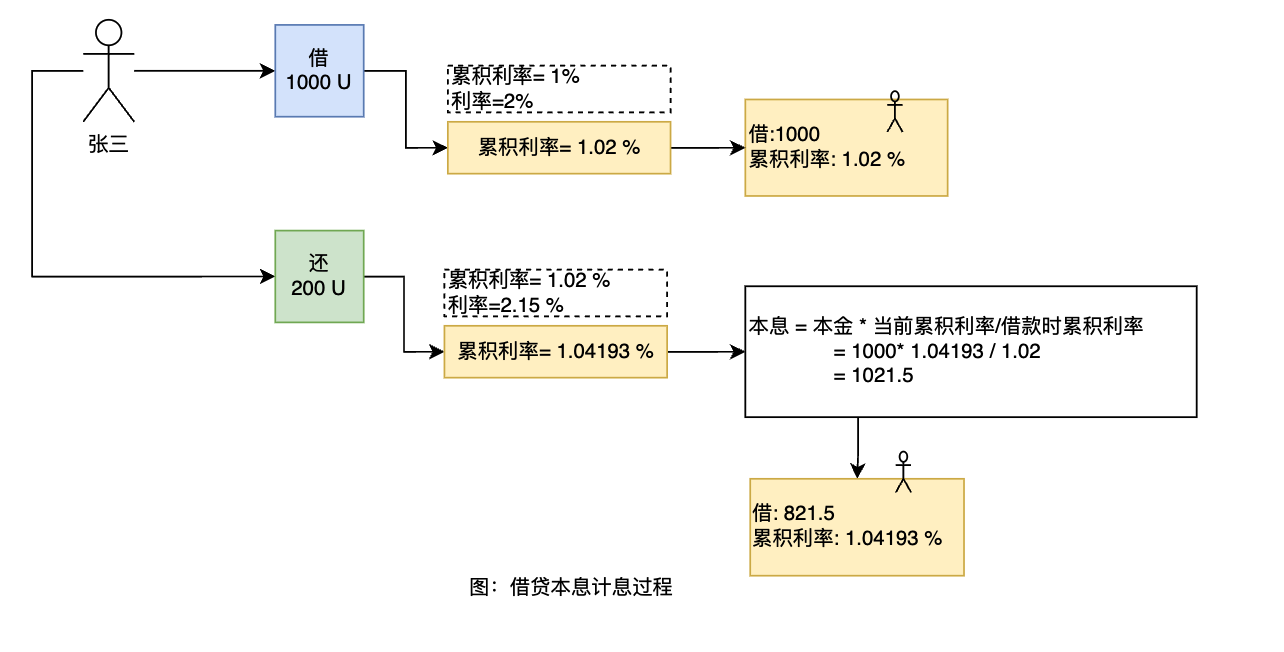
当张三第一次借出1000 U 时,先更新累积利率从1%更新到 1.02%,然后在账簿上记录张三借款本金1000和此时刻的累积利率 1.02%。一个小时后,张三还入200U。假设这一小时没有其他借贷发生,这一小时的借款利率是2.15%,累积利率更新成 1.04193%。根据当前的累积利率计算出张三的借款本息为 1021.5 U 。最后,除去200U还款,更新账簿上张三新的借款本金为 821.5 U,并同步更新累积利率。
Compound就是通过这种简单方式维护着借款账簿,只需维护好累积利率,便可实时的追踪每位借款人的本息。
思考
- 你会将资产存入高流动性还是低流动性的借贷协议中?
- 你有办法提高自己在借贷协议中的收益吗?

- 链上金融,用向五岁小孩解释的方式 383 浏览
- 第6章:去中心化借贷 2100 浏览
- 加密货币杠杆状况——2025年第三季度 4122 浏览
- 第10章:去中心化彩票 1592 浏览
- 第6章:去中心化借贷 1766 浏览
- 推荐的 DeFi 资源网站 1861 浏览
- 第2章:什么是去中心化金融 (DeFi)? 1672 浏览
- 一个 Compound 提案解码器 566 浏览
- FlyingTulip FT 融资详解 1239 浏览
- 加密货币支持的贷款 555 浏览
- AAVE V3 DeFi 集成技巧 2046 浏览
- 收益耕作:顶级策略、风险与安全提示 675 浏览

